采用层次分解策略的多机协同航路规划

叶文，赵建忠，吕晓峰，刘华文

(海军航空大学 兵器科学与技术系，山东 烟台 264001)

0 引言

无人机作战的主要模式是多机协同作战，而多机协同航路规划是提高无人机作战效能的有效手段。多机协同航路规划就是在考虑装备性能和设备精度限制的条件下，为无人机规划出飞行航路，确保得到的航路满足协同要求，并具有较好地生存概率[1-3]。

1 多机协同航路规划的数学模型

多机协同航路规划是在保证无人机高生存概率的条件下，为每架无人机规划出飞行航路，并满足无人机同时到达或者间隔到达的协同要求[4-7]。最终每架无人机规划得的航路，对无人机自身来说不一定是最优的，然而针对无人机编队来说，却一定是最优或接近最优的。

评价规划得到的协同航路优劣的性能指标主要包括燃油性能指标(燃油代价最小)和安全性能指标(威胁代价最小)。

燃油代价：

威胁代价：

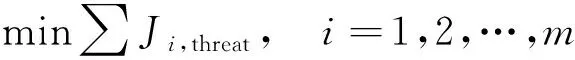
则多UCAV协同航路规划的总性能指标为

式中：k为加权系数。

多机协同航路规划还需要满足一定的约束条件，包括单机的物理性能和单架无人机的任务需求，而且还要满足多机同时达到目标约束和无人机之间最小安全距离约束等。主要包括最大作战半径约束、最小转弯半径约束、禁飞区约束、时域协同约束和空域协同约束。

2 基于层次分解策略的协同控制

多机协同航路规划与单机航路规划相比，主要是空域协同和时域协同的实现问题。其中，时域协同主要是确保飞机按照一定的时间要求到达各自的目标点。时域协同一般分为以下3种情况[8]：

(1) 同时到达：编队的所有飞机在相同的时间点同时到达各自所要攻击目标的攻击点，对同一目标或者不同目标实施同时攻击。

(2) 严格依次顺序到达：编队的所有飞机按照一定的先后顺序依次到达所要攻击目标的攻击点，并且各个飞机到达的时间节点有严格精确的要求，即一架飞机到达攻击点后，t时间后下一架飞机必须到达攻击点，不能提前也不能推迟。

(3) 松散依次顺序到达：编队的所有飞机按照一定的先后顺序依次到达所要攻击目标的攻击点，并且各个飞机到达攻击点之间的时间间隔有范围要求，即一架飞机到达攻击点后，下一架飞机必须在[tmin,tmax]时间范围内到达攻击点，不能超出这个可接受的范围。

目前，要求同时到达是多机协同航路规划中最常见的情况。一般，采用层次分解的思想来进行同时到达情况的求解。即多机的协同航路规划分解为航路规划层、协同控制层、平滑处理层3个层次，如图1所示。航路规划层首先为每架无人机规划出Num条可选航路，形成备选航路集合；协同控制层根据协同函数和协同变量，为每架飞机从其Num条备选航路中选择一条合适的航路，组成协同航路，使得得到的航路满足协同要求；平滑处理层主要是对航路进行平滑处理，使其满足最小转弯半径约束，并不改变其航程，确保同时(依次)到达目标。

3 基于小生境克隆选择算法的单机多航路规划

在多机协同航路规划层次结构中，必须对单机多航路规划技术进行研究。单机多航路规划要求能够规划得到多个全局次优航路或者有意义的局部最优航路，从而得到不同的Num条可选航路[9-11]。

免疫系统作为一种分布式自学习系统，其通过B细胞的高变异克隆，以及进化处理不同抗体，实现各种抗体并存，从而使系统保持良好的多样性。根据免疫系统的基本原理，人们提出了免疫克隆选择算法，并将其应用于多峰值优化问题的求解中[12-13]。免疫克隆选择算法主要包括克隆扩增、克隆变异和克隆选择操3个步骤。但是，免疫克隆选择算法存在易陷入局部最优、后期收敛速度慢等缺陷。本文通过在免疫克隆选择算法中引入小生境技术，并对算子进行改进操作(记忆算子、抑制算子和重组算子等)，用其来求解单机多航路规划问题。

具体算法描述如下：随机产生N个抗体组成初始化抗体群，计算每个抗体的抗体-抗原亲和度，将每个抗体的亲和度与记忆阈值δm进行比较，大于阈值的抗体存到记忆库中，并进行抑制操作；对每个抗体的亲和度进行适应值共享函数调整；对调整后的抗体进行克隆扩增和重组变异操作；计算扩增和变异后的抗体亲和度，由每一个子群中的最优抗体组成新的抗体群；随机生成Ns个新的抗体，替换新的抗体群中亲和度低的Ns个抗体。

单机多航路规划算法的实现流程如图2所示。

基于小生境克隆选择算法的单机多航路规划的具体实现见参考文献[14]。

4 协同变量与协同函数

在层次分解策略下，首先采用小生境克隆选择算法为每架无人机生成了Num条备选航路，下一步就是要根据航路的协同要求，在每架无人机的Num条备选航路中选择一条航路。在进行航路选择时，必须既要满足多机之间的协同要求，又要尽量使整个编队航路整体最优。选择航路的估计到达时间(estimated time of arrival，ETA)来对每架无人机的航路进行协同[15]。

假设v∈[vmin,vmax]为飞机的速度区间，那么对于飞机i规划得到的航路Lj，则其预计到达时间为Tj∈[Lj/vmax,Lj/vmin]。这样，对于飞机i的Num条备选航路，其预计到达时间则是Num个时间范围的并集Si。

Si= [L1/vmax,L1/vmin]∪[L2/vmax,L2/vmin]∪…

∪[LNum/vmax,LNum/vmin].

假设编队由N架飞机组成，若时间交集S=S1∩S2∩…∩SN，如果S不为空集，即存在Ta∈S，则说明对于估计到达时间Ta来说，在每架飞机的Num条备选航路中都能找到一条估计到达时间为Ta的航路。因此，如果每架飞机都选择估计到达时间为Ta的航路飞行，则能满足同时到达要求，所以称Ta为协同变量。

由于时间交集S是一个集合，而不是一个数，因此估计到达时间Ta不唯一，即可能存在多条可选择的航路，那么怎样选值来确定协同变量的值呢？这里，通过构建协同函数Jxt来确定对协同变量值。

Jxt,j(Tj)=k1Jj+k2Tj，

式中：k1，k2为系数；Jj为具体航路的代价，对于确定的一条航路，Jj是一定的，Jj=kJthreat+(1-k)Jfuel。因此，对于每一条航路的Jxt,j都是估计到达时间Tj的函数。无人机编队的总体代价为

式中：N为飞机的数目。

根据代价函数，时间不同，航路的代价Jxt也随着变化，代价Jxt与协同变量Ta的关系如图3所示。

Jxt称为协同函数。

在协同控制层中，首先建立Jxt，根据代价最小的原则，选择确定合适的Ta。然后根据选定的Ta，在每架无人机Num条备选航路中选择相对应的一条航路，最终得到多机的协同航路。

5 仿真验证与分析

假设3架无人机协同攻击1个目标，战场态势示意图如图4所示，无人机速度范围均为40～60 m/s。首先采用小生境克隆选择算法为每架无人机规划各自3条分散的最优及次优航路，如图4，5和6所示。ETA的最优决策如图7所示。协同时间ETA取2 924 s时，即保证3架无人机同时到达目标点。最终得到的协同航路如图8所示，表1为规划结果统计。

表1 协同航路信息Table 1 Cooperation path information

6 结束语

将层次分解策略与小生境克隆选择算法相结合，先采用小生境克隆选择算法为每架无人机自主地规划多条离散的可选航路，再通过协同变量和协同函数，实现航路的协同控制，最终确定编队的协同航路，有效解决了复杂战场环境下多机协同航路规划问题，为该问题求解提供一种新的有效方法。