一种装备体系作战试验综合能力评估方法*

2018-08-22徐海波邹建华汪彩玲陈国利

火力与指挥控制 2018年7期

徐海波，邹建华，汪彩玲，陈国利

（1.西安交通大学电子与信息工程学院，西安 710049；2.中国白城兵器试验中心，吉林白城 137001；3.中国远洋航天测量船基地，江苏江阴 214400）

0 引言

开展武器装备作战试验时，当利用获取的数据对武器装备的作战效能和作战适用性进行评估时，我们面临与以往试验有很大不同的一系列问题。其中一个问题是，能否利用类型不同、数量庞大的数据对装备体系的综合能力给出一个单一数值的定量评估结果，从而为评价、比较、研究装备体系提供基于现场试验的综合技术依据。本文围绕该问题，利用层次分析与模糊量化相结合的方法对试验数据进行分析计算，完成对某装备体系综合能力的评估。

1 评估总体思路

评估总体思路是，利用试验获取的所有底层指标数据进行综合，给出综合能力的单一数值大小［1］。此数值介于0与1之间，1代表构成综合火力的各类武器装备在完成所拟定的想定任务条件下其能力能够发挥百分之百。

评估时，首先根据某装备体系组织结构特点及火力运用特点建立指标体系层次分析结构模型，然后据此确定全部指标权重，并根据作战试验结果和历史试验数据确定最底层指标的隶属度。

确定指标权重包括构造比较判断矩阵、求取单一准则下元素相对权重、求取群组决策时的权重、求取底层指标层元素对于目标层的合成权重等计算过程，确定指标的隶属度包括建立隶属函数模型、性能指标的无量纲化和归一化处理、定性指标的量化处理等计算过程。最后，将所有底层指标合成权重与对应的隶属度采用加权和法进行综合，得到综合火力运用能力评估结果。在装备体系综合能力评估过程中，可按同样的定义和方法分别给出组成装备体系的野战防空装备、压制装备、步兵装备、反装甲装备各自的综合能力评估结果。

在此基础上，定义野战防空、压制、步兵、反装甲装备各所属底层指标合成权重与对应隶属度的加权和相对于装备体系综合能力大小的比值为其对装备体系综合能力的体系贡献率。

2 评估方法

建立指标体系层次分析结构模型后，按以下步骤和方法进行计算评估。

2.1 构造比较判断矩阵

假定以上一层元素C为准则，其所支配的下一层的元素为 u1，u2，…，un，现要根据它们对于准则的相对重要性赋予u1，u2，…，un相应的权重，采用两两比较判断法求出权重。

两两比较判断就是要反复回答如下问题，针对准则，两个元素哪一个更重要，重要多少，并按1～9比例标度对重要性程度赋值。这样，对于该准则，当全部完成n个元素中任意两个元素的比较判断后，比例标度构成了一个两两比较判断矩阵A［2］，即

之后，对判断矩阵进行一致性检验。

2.2 求取单一准则下元素相对权重

设相对权重

矩阵A的特征方程为

设w'为矩阵A的最大特征根所对应的特征向量，则有

求出w'后，对其进行归一化［3］

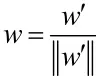
即可求得相对权重w。

2.3 求取群组决策时的权重

设对同一个准则，有m位专家参与判断，他们的判断矩阵分别为 A1、A2、…、Am，其中

采取几何平均综合判断矩阵法求取综合权重向量。将m个判断矩阵，用几何平均的方法获得一个综合判断矩阵A，其中

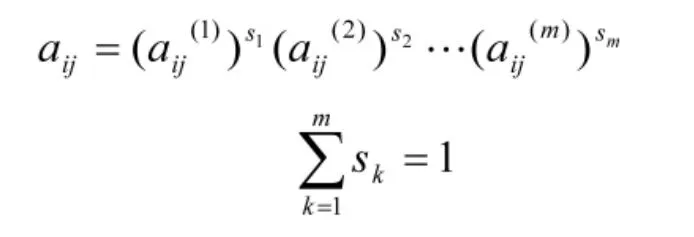
式中，sk为各个专家的权重系数，取sk=1/m，此时

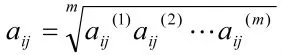
从而得到综合判断矩阵A，求出A的主特征向量作为综合权重向量［4］。

2.4 求取对于目标层的合成权重

合成权重的求取按照自上而下的方向，将单准则下的权重进行合成。

假设已经计算出第k-1层上nk-1个元素相对于总目标的排序权重向量

第k层上nk个元素对第k-1层上第j个元素为准则的排序权重向量设为

其中不受j支配的元素的权重为0。设

它是nk×nk-1的矩阵，表示k层上元素对k-1层上各元素的排序，则第k层上元素对总目标的合成排序向量由下式确定［5］

一般地有

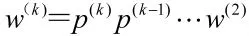
式中，w（2）为第二层上元素对总目标的排序权重向量，实际上它就是单准则下的权重向量。

2.5 性能指标无量纲化和归一化处理

性能指标的无量纲化和归一化处理，应用模糊数学中的隶属度和隶属函数的概念与方法来进行。有多少项性能指标就相应地建立多少个隶属函数。隶属函数可以选择钟形分布、升半梯形分布、降半梯形分布、三角形分布等。具体选取哪种类型的隶属函数，需通过分析性能指标的属性，即性能指标值以何种方式影响评价结构来确定。

即使为某两项性能指标选取了同一类型的隶属函数，但由于性能指标值的量纲和（或）取值范围不同，隶属函数中有关参数的取值也就不同，即隶属函数的具体表达式是不同的。

对于要求越大越好的结果数据，采用如下形式的效用函数

对于要求越小越好的结果数据，采用如下形式的效用函数

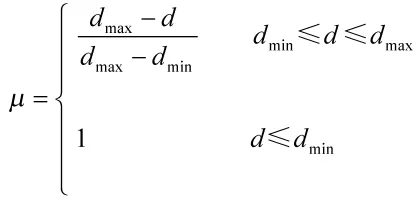
2.6 定性指标的量化处理

定性指标的权重确定方法与定量指标相同，如前文所述。对于隶属度，采用模糊评判法进行定量处理。

给定评语集

表示定性指标的模糊性和不确定性，并用实数集

表示对评语集的模糊量化结果。

指标的隶属度μi，取m位调查对象评判结果的算术平均值并进行归一化，即

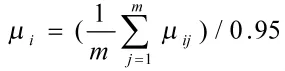
2.7 指标综合

对目标层采用加权和法对各类指标进行综合，即

式中，E即为装备体系综合火力运用能力。

各类装备对装备体系综合能力的体系贡献率按下式进行计算。

3 算例分析

3.1 建立某装备体系指标体系层次模型

根据某装备体系组织结构特点及火力运用特点建立了由825项指标构成的综合能力指标体系层次分析模型，其中包含544项最底层指标［6］。在该层次模型中，同一层次的元素作为准则对下一层次的某些元素起支配作用，同时它又受上一层次元素的支配，这样就形成了层次间自上而下的逐层支配关系。最高层即目标层的元素就是“某装备体系综合能力”，第2层的元素是“野战防空能力”、“压制能力”、“步兵能力”、“反装甲能力”，第3层的元素是在每个第2层元素的下面都按“指控能力”、“侦察能力”、“打击能力”、“机动能力”、“保障能力”等5个元素向下发展，依此类推，直至最多达11层。最底层元素表示为实现目标可供选择的各种可测试指标，如“通信成功率”、“战斗准备时间”、“截获率”、“反应时间”、“射击精度”等［7-8］。

3.2 计算过程及结果

评估时选取21名专家对指标重要性进行了判断，形成了1 202个判断矩阵。采取方根法求取w'，并求出综合判断矩阵的主特征向量作为综合权重向量。

依据2.1～2.4节中所述方法开发了权重计算程序。权重计算程序按照“指标层数不限”、“指标个数不限”、“专家人数不限”、“操作简单灵活”、“运行稳定可靠”、“计算精确高效”的设计思想进行开发。系统由指标管理、专家管理、打分和结果处理等4个模块组成。使用Visual Studio 2008集成开发平台，采用面向对象技术和模块化技术进行软件开发。开发语言为C#3.0，基于Microsoft.NET3.5程序框架，数据的读取与保存除XML文档外，其余均通过数据库来完成，数据库采用Access2010。

利用计算程序计算出所有最底层指标的合成权重。

依据2.5节中所述方法对所有544项底层指标（定性指标除外）分别建立隶属函数模型，根据作战试验结果和历史数据逐一计算出隶属度。

依据2.6节中所述方法对试验获取的653份定性指标数据调查表进行处理，得到所有定性指标的隶属度。

按2.7节中所述方法分别计算出某装备体系综合火力运用能力、构成该装备体系的各类武器装备对装备体系综合能力的体系贡献率，评估结果如下：

某装备体系综合火力运用能力大小为62.3%，其涵义为构成该装备体系的各类武器装备在完成所拟定的想定任务条件下其综合能力能够发挥62.3%。其中，野战防空综合能力大小为68.7%，对装备体系综合能力的体系贡献率为29.4%；压制综合能力大小为64.4%，对装备体系综合能力的体系贡献率为21.9%；步兵综合能力大小为54.2%，对装备体系综合能力的体系贡献率为28.6%。反装甲综合能力大小为54.4%，对装备体系综合能力的体系贡献率为20.1%。