复杂舰船目标毁伤评估模型建立方法研究

马晓明，晏卫东，刘延青

（解放军92941部队，辽宁 葫芦岛 125001）

0 引言

舰船作为海战中重要的作战平台，一直受到各个国家的高度重视，其毁伤效果的评估是一项极为重要的工作［1］。目标毁伤效果评估是指依据作战目的对目标实施一定火力打击后，对目标毁伤效果或程度进行定性或定量评定。舰船目标的多样性，舰船本身各系统规模庞大，同时反舰导弹要对舰船目标造成一定程度的毁伤，命中目标只是前提条件，因为反舰导弹的毁伤能力还与战斗部威力、命中舰船目标的部位、船体防护模式以及舰船目标的任务性质等多种因素有关。

贝叶斯网络（Bayesian Networks）可以根据已知的不确定或不完整的信息对所要研究的问题进行准确的推理，同时可对实弹试验或仿真试验中获取的多种毁伤结果信息进行多层次处理，较好地降低了由于毁伤环境的复杂性和毁伤结果的不确定性造成的信息融合结果的不确定性［1］，可使其较好地被用在靶场或战场上根据各种可知的不确定或不完整的目标舰船毁伤信息，对敌舰船目标毁伤效果进行综合评估［2］。为此，本文将基于贝叶斯网络技术对复杂舰船目标毁伤效果评估模型的建立方法及应用进行研究。

1 贝叶斯网络理论

贝叶斯网络是一种概率网络，以贝叶斯公式为基础，将基于概率推理网络图形化。所谓概率推理就是通过已知一些变量的信息，通过分析变量间的关系获取其他未知的变量概率信息的过程，基于概率推理的贝叶斯网络是为了解决不确定性和不完整性问题而提出来的，已广泛地应用于多个行业领域［3］，对于解决复杂系统的毁伤状态评估有很大的优势。

1.1 贝叶斯网络表示

贝叶斯网络是用来表示一组变量之间概率依赖关系的有向无环图S=＜N，A，Θ＞，这里每个节点n∈N表示域中各个变量，每条边a∈A表示每两个变量之间相互关系的依赖性，同时每个节点都具有各自的条件概率分布（Conditional Probability Distribute table，CPT），它明确了该节点（变量）与其所有父节点之间的概率相互依赖的数量关系，Θ表示CPT参数。从定性的角度分析，贝叶斯网络采用有向弧线表示节点间的直接因果关系。因此，贝叶斯网络能够较好地表达和解释那些事件之间相互关系无法明确表示和处理的问题。从定量角度分析，贝叶斯网络是各变量间概率关系信息的载体，是变量概率联合分布的图形化表示［3］。

1.2 贝叶斯网络推理问题

推理是依据某种规律进行计算来回答查询的过程。贝叶斯理论是贝叶斯网络推理的原理，利用随机变量间的条件独立性，将一个事件总的网络联合概率分布直观形象地表达成一个图形结构和一系列节点的条件概率表，经消元（消除变量）计算可计算推导出网络中任一变量的概率分布或部分变量的概率分布，其核心内容是计算网络后验条件概率分布。在已知网络中某些节点变量证据的取值情况下，可计算推理出关心的网络节点变量或节点变量集合的条件概率分布。

若设网络所有变量的集合为X，证据变量的集合为E，查询变量的集合为Q，则贝叶斯网络推理的任务就是计算在给定的证据变量集合E=e的情况下计算推导出查询变量Q的条件概率［4］。可形式化描述为：

2 目标舰船各舱室命中概率分析

导弹对目标舰船的命中情况直接影响舰船的毁伤结果，其中对各舱室的命中概率决定了评估贝叶斯网络底层节点的初始概率分布参数，因此，有必要对其进行分析研究。通过采用蒙特卡洛法进行导弹模拟打靶并对结果统计分析，得到目标舰船各毁伤工况的发生概率，即对目标舰船各舱室单元的命中概率，并将其融合到最终的毁伤结果评估中。

2.1 蒙特卡洛法模拟打靶试验

蒙特卡洛法又称统计模拟法或随机模拟法，是一种利用随机变量的随机模拟试验求近似解的数值方法。对于导弹武器射击误差评定来说，导弹飞行打靶试验复杂而又耗费巨大，且试验统计数据不足，应用蒙特卡洛法在计算机上进行导弹的数学模拟打靶，预测命中精度，可以较好地解决此问题，从而达到辅助求解导弹射击误差的目的［5］。

图1 舰船目标空间统计单元划分示意图（n=50）

表1 目标舰船舱室命中数仿真结果统计数据

对舰船目标模型进行空间划分，将船体纵向每一个舱室作为一个统计命中点的分析单元，共划分为50个单元（n=50）；具体划分的示意图见图1所示，将目标舰船简化为对称中轴面的长方体空间，取中轴面y坐标为0，整艘舰船的坐标原点取在船舯底部，空间坐标划分见表1。采用国外某型导弹制导飞行通用数学模型和系统方程，将各随机干扰变量的抽样值输入系统方程，进行模拟打靶，获得导弹落点的样本观察值。

根据获得的试验结果数据和舱室坐标判断每次模拟打靶的命中舱室情况，统计得到舰船目标各舱室命中次数及命中概率估值。

3 舱室内爆毁伤规律分析

导弹命中某一舱室后，舰船各舱室具体毁伤程度及规律，需通过具体试验或仿真计算等手段获取相关数据进行分析。采用对简单舱室内爆超压和典型舰船毁伤工况的冲击环境进行数值计算，评估舱室的毁伤情况，总结该型导弹命中该目标舰船后舱室的毁伤规律，为确定毁伤评估贝叶斯网络底层节点参数提供支持。

3.1 舱室内爆超压毁伤分析

选取目标舰船模型中纵向相邻的6个舱室，对模型进行局部数值仿真计算。导弹战斗部在最右侧舱室中央爆炸，模型工况如图2所示。计算结果应力响应云图如图3所示。

图2 舱室计算示意图

图3 应力响应云图

从图3中可以看出，当t=0.05 ms时，载荷首先作用在命中舱的舱壁上；当t=0.1 ms时，该舱壁的中央区域发生撕裂失效；当t=0.15 ms时，在冲击波作用下，爆源舱室舱壁出现大破口，冲击波压力传播到了舱室1；当t=0.3 ms时，舱室1的舱壁出现较大破口，隔板2发生塑性变形；当t=0.5 ms时，隔板2的中央区域发生撕裂产生破口；随着冲击波载荷的传播，在t=0.85 ms时，隔板3发生塑性变形，并未产生破坏。产生破口的舱室会对其内部人员及设备造成巨大的破坏作用，同时对舰船的局部和总体强度有较大的影响，结构产生塑性应变的舱室涉及到内部人员和设备的状态变化，可对舱室损毁规律进行分析归纳［6-7］。

3.2 舱室内爆炸冲击环境分析

为了进一步分析总结舱室毁伤规律，有必要对没有发生舱壁破口或撕裂的舱室进行冲击环境的分析，以总结出舱室及内部设备的毁伤状态。分别选择船艏、船舯和船艉3个典型命中工况，进行舱室内部爆炸冲击响应计算，得到船体典型位置附近加速度等相关参数，并且采用冲击谱对冲击响应结果进行处理。下页图4为船艏、船舯和船艉3种典型工况毁伤效应仿真计算结果。

根据对执行作战任务的影响程度，结合有关舰船毁伤试验评估经验，对比相关标准将每个舱室毁伤状态定义为4种等级：轻度（I级）、中度（II级）、重度（III级）、报废（IV级）［6］。通过仿真数据分析可知第2邻舱虽然舱壁没有完全破损，但冲击环境较为恶劣，同时受部分冲击波超压作用，在此种环境下舱内人员会受到较为严重的伤害，所含设备出现较为严重毁坏；第3邻舱舱壁没有破损，冲击环境严酷度有所降低，在此种环境下舱内人员会受到一定伤害，设备也会造成一定毁坏；第4邻舱冲击环境严酷度较低，在此种环境下舱内人员会受到轻微伤害，设备完好率较高。因此，可总结出该型导弹命中该目标舰船后舱室的毁伤规律：命中舱及相邻舱为报废级别；隔舱划分为严重毁伤级别；第2隔舱划分为中度毁伤级别；其他舱室划分为轻度毁伤级别。

4 贝叶斯网络模型建立

4.1 网络结构确定

根据目标舰船及其设备物理结构、功能结构的组成，依据各系统工作流程确定各系统和设备的聚合关系、先决关系，构建贝叶斯网络结构图。主要分为4个层次：舰船总体结构、各主要系统结构、分系统结构和设备舱室层。根据各系统及所属设备的划分，分析确定各设备的舱室编号。应用GeNIe贝叶斯推理软件，依次将各舱室与所属系统相连接，建立目标舰船贝叶斯网络结构。

4.2 网络节点参数确定

贝叶斯网络模型参数包括节点状态的确定和条件概率的确定两方面内容。节点条件概率分布的确定一般都比较复杂，通常由专家凭经验确定或由统计试验确定。贝叶斯网络必须明确定义每一个节点所有可能的状态及依附在其上的条件概率。根据对执行作战任务的影响程度将每个层次节点的状态均划分为4种毁伤等级：轻度（L级）、中度（M级）、重度（H级）、报废（F级）。设备舱室毁伤等级与所需维修时间对应关系准则制定如表2所示。

图4 典型工况仿真计算结果

表2 各舱室毁伤级别准则

4.2.1 第1层节点参数确定

该网络第1层节点主要由50个独立的舱室组成，共有50个节点。综合蒙特卡洛模拟打靶结果和对舰船舱室毁伤规律的结论，得到该层节点各等级毁伤概率，其中系统各设备的毁伤等级可等同于所属舱室的毁伤等级。

如3号舱室的邻舱分别为第2、4、15、16和17号舱室，根据舱室毁伤规律可知，这些舱室被导弹命中后，第3号舱室毁伤级别均为报废状态F，因此，求出它们的命中数之和N3F，再比上模拟打靶的总命中次数Nm就得到3号舱室报废概率P3F，计算过程如下：

同理，3号舱室重度毁伤概率P3H：

3号舱室中度毁伤概率P3M：

3号舱室轻度毁伤概率P3L：

依照以上方法对目标舰船1～50舱室各级毁伤概率计算结果的统计。

将第1层各节点每个状态及参数依次输入贝叶斯网络相应节点，作为网络节点初始概率。

4.2.2 第2层节点参数确定

网络第2层节点主要由17个分系统组成，共有21个节点。根据实际情况，假设其中每个分系统所含设备舱室均具有串行工作关系，它们的各毁伤状态等级概率采用计算统计各自维修时间的方法进行确定。

令分系统节点（子节点）各种状态的维修时限为Tsis～Tsie，相应第1层节点（父节点）各种状态的维修时限为 Tfis～Tfie。子节点最大维修时限为 Tss～Tse，且，则在父节点处于第i种毁伤度时，子节点发生某种毁伤度的条件概率计算方法为：

其中，Tsis为该子节点第i种状态的最小维修时限；Tsie为该子节点第i种状态的最大维修时限；Tfis为第i个父节点的最小维修时限；Tfie为第i个父节点的最大维修时限；Tss为子节点的最小维修时限；Tse为子节点的最大维修时限；Pa（A）为子节点A的父节点。

以反舰导弹武器系统节点毁伤条件概率计算为例，当反舰导弹武器系统所属舱室节点（21、22、31）毁伤状态均为 L（轻损）时，根据式（3），该系统此种状态下的各个毁伤状态的条件概率计算如下：

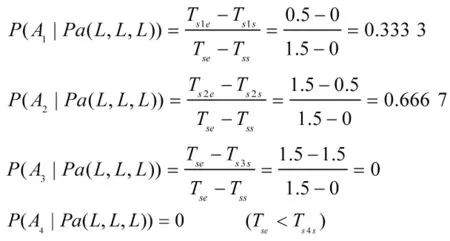
即轻损L概率为0.3333，中损M概率为0.6667，重损H和报废F的概率为0。同理依次计算出该分系统所属舱室节点各不同毁伤状态组合（共64种）的各毁伤等级条件概率。

根据舱室分布统计和实际工作流程分析，可知分系统所包含设备均具有串行工作关系，采用以上方法依次计算出各分系统节点条件概率。

4.2.3 第3层节点参数确定

网络第3层节点主要由五大系统组成，共有5个节点。

1）串联关系系统节点条件概率

如推进系统所包含的3个分系统能源发生系统、推进机组和推进保障系统工作流程上具有串行关系，因此，该系统毁伤状态各等级概率采用统计计算维修时间的方法进行确定。依次计算出该系统所属分系统的各不同毁伤状态组合下（共64种组合）的各毁伤等级条件概率。

2）并联关系系统节点条件概率计算

除了推进系统，其他4个系统武器系统、船体结构、电力系统和警戒与指挥系统所包含的分系统工作流程上均具有并行关系，此4个系统毁伤状态各等级概率采用1～9标度对比的方法进行权重确定。以武器系统为例，构造其各分系统判断矩阵如表3所示，权重计算结果如表4所示。

表3 武器系统各分系统判断矩阵

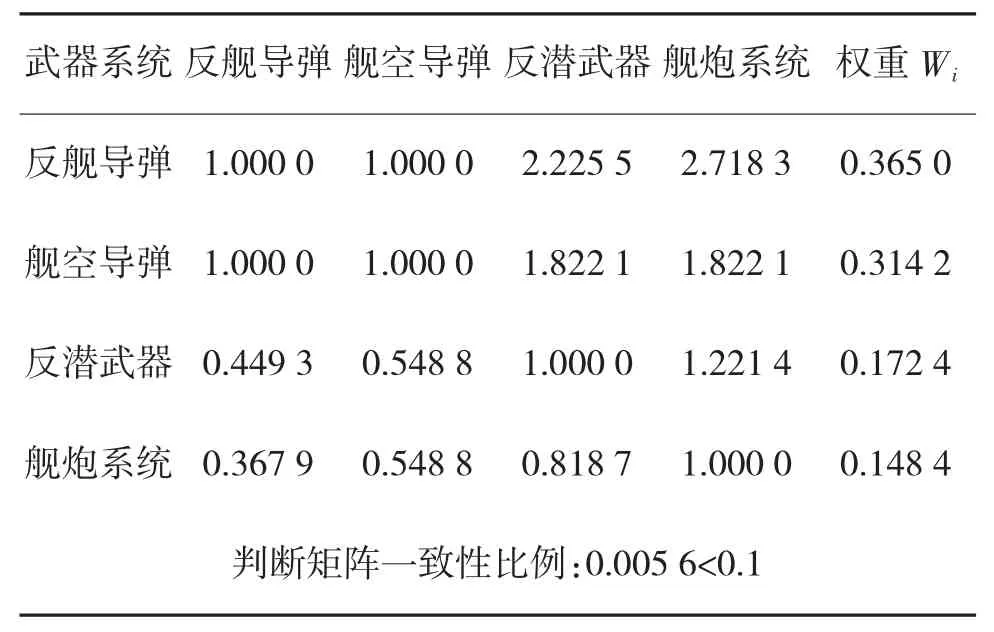
表4 武器系统1～9标度权重计算结果

由此可得武器系统所包含的4个分系统各种不同毁伤状态组合下（共256种组合）的各毁伤等级条件概率，计算结果如表5所示。

表5 武器系统节点毁伤条件概率参数计算结果（部分）

4.2.4 第4层节点参数确定

网络第4层只包含一个节点即评估的最终的目标舰船总体毁伤节点。该节点中五大系统分别具有不同的作战功能，在执行作战任务过程中担负不同的使命任务，各系统间工作流程相对独立［8-10］，因此，舰船总体毁伤节点的各等级毁伤状态概率采用1～9标度权重对比的方法进行确定。

根据1～9标度对比的方法，各系统判断矩阵构造如表6所示，计算结果如表7所示。

表6 舰船总体各系统判断矩阵

由此可得舰船总体所包含的4个分系统各种不同毁伤状态组合下（共1 024种组合）的各毁伤等级条件概率。计算结果如表8所示。

将以上4层节点所包含的条件概率分布参数输入所建立的贝叶斯网络结构模型相应节点后，得到该典型舰船目标毁伤评估贝叶斯网络模型，如图5所示。

该舰船目标毁伤评估贝叶斯网络模型共包含77个网络节点，308个毁伤等级状态，84条节点因果关系射线，3 218个毁伤状态组合和12 872个状态参数。

表7 警戒与指挥控制系统1～9标度权重计算结果

表8 舰船总体毁伤条件概率参数计算结果（部分）

4.3 全工况毁伤概率推理计算

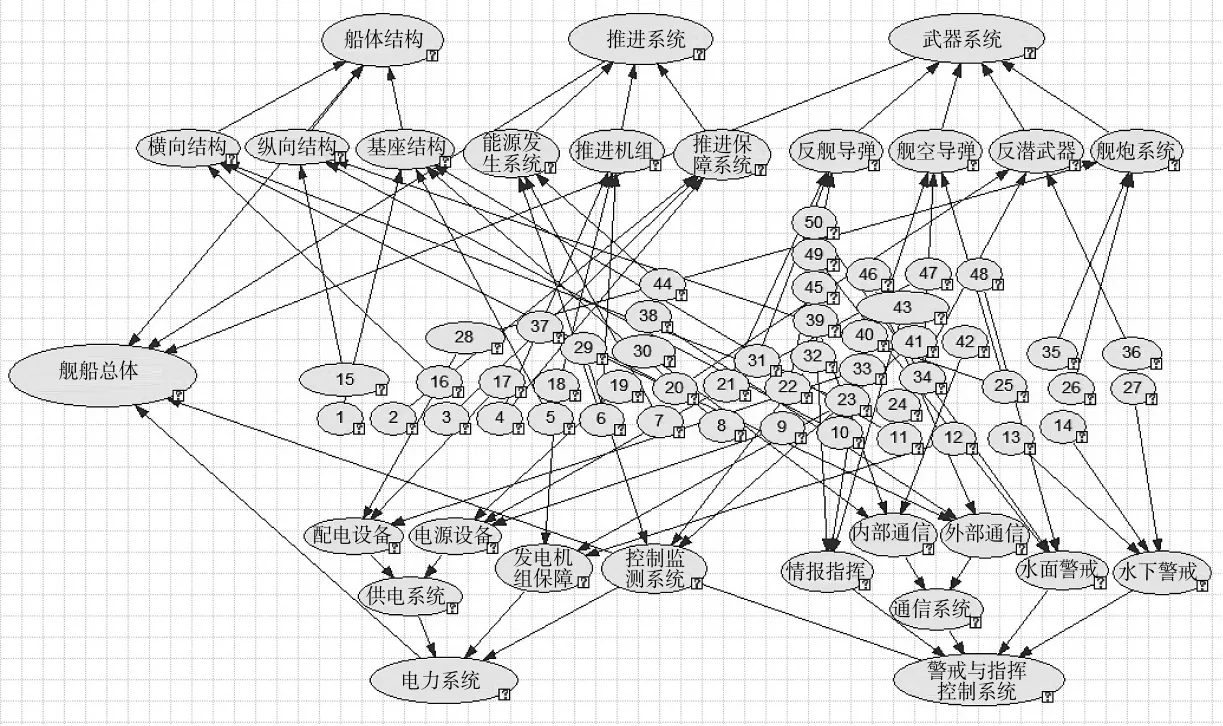
图5 典型舰船目标毁伤评估贝叶斯网络模型

通过4.2节的各毁伤工况仿真计算结果，统计出该型舰船各舱室的毁伤规律，并结合表5中对舰船目标的舱室分布统计，利用建立好的贝叶斯网络模型，输入各工况的初始状态，即反舰导弹命中某一舱室后的全舰各个舱室的毁伤状态，通过贝叶斯网络推导出舰船总体的各毁伤概率。

以031工况为例，当导弹命中第31舱时，本舱和临舱 21、22、31、32 为报废状态，隔舱 7、8、9、20、30、39 为重度毁伤状态，第 2 隔舱 6、19、23、33、38、40、43、44、45为中度毁伤状态，其他舱室为轻度毁伤状态。将此时1～50舱室状态作为证据输入贝叶斯网络模型，进行推理计算，更新网络各节点状态参数，得到舰船目标总体毁伤概率P（A）为：

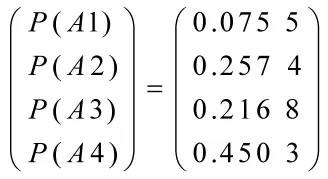
即轻度毁伤概率0.0755，中度毁伤概率0.2574，重度毁伤概率0.216 8，报废概率0.450 3。

分别将001～050工况下1～50舱室状态作为证据依次输入所建立的贝叶斯网络评估模型，并依次推理更新网络其他各系统节点毁伤状态参数，进而得到每种工况下的目标舰船总体毁伤概率，如表9所示。

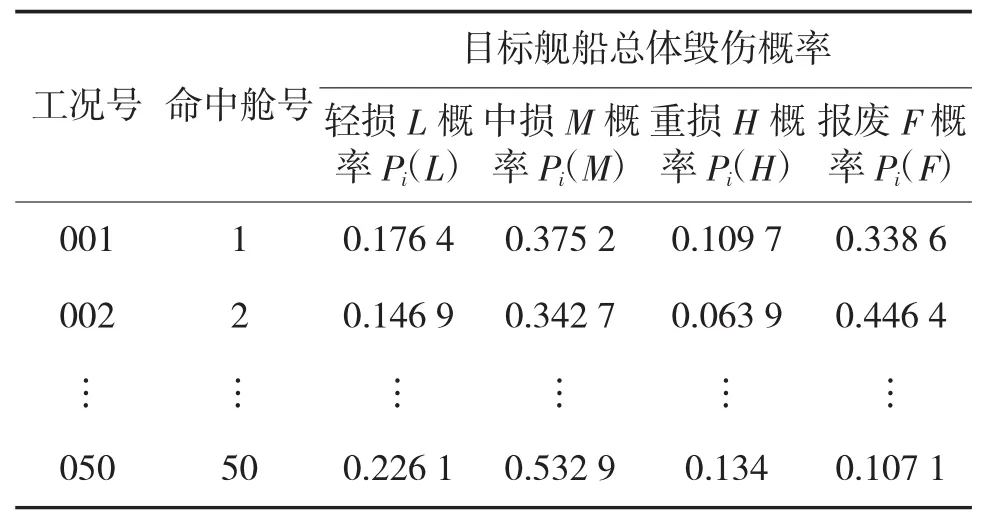
表9 全工况舰船总体毁伤概率计算结果（部分）

导弹命中该舰船目标时，001～050每种工况的发生概率（即每个舱室的命中概率）P（mi），可由表3得到。则舰船目标各毁伤等级概率：

轻度毁伤概率：

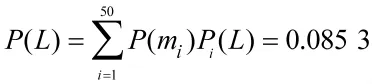
中度毁伤概率：

重度毁伤概率：

报废概率：

舰船目标的毁伤概率分布如图6所示。

图6 舰船目标被击中后毁伤概率分布图

5 结论

利用该评估贝叶斯网络，较好地推理计算了模型中所有可能工况的毁伤结果，得到全工况舰船目标总体毁伤状态表，在实际应用中，作战指挥人员可根据实际的打击工况快速评估舰船的毁伤状态，为制定下一步作战计划提供参考。舰船设计人员可根据推理结果，分析确定较为严重和较轻的工况，合理排布舰船各系统设备的分布设置，或提高舰船敏感部位的防护等级，以提高舰船在执行作战任务过程中的生存能力，提升综合作战效能。该方法为舰船毁伤和导弹威力的评估提供有效途径，充分利用了数值仿真计算的海量数据，挖掘出隐藏于数据之间的逻辑关系并充分加以利用。