基于数值仿真的顺层岩质边坡支护稳定性分析

林 一 夫

(中铁西北科学研究院有限公司， 甘肃 兰州 730000)

随着人类工程建设活动的日益增加，顺层岩质边坡治理问题已成为矿坑治理工程中常见的工程地质问题。由于岩质边坡稳定性受岩体岩性、结构面、层面和地下水等相关因素控制，同时岩质边坡岩体中含大量产状和特性复杂的不连续面，如层面、节理、裂隙、软弱夹层、岩脉和断层破碎带等，造成岩质边坡稳定性计算的困难[1]。因此，合理判辨这些相关因素成为岩质边坡稳定性分析的重难点。

目前，业内对于岩质边坡的稳定性分析主要采用理论计算和工程地质类比法。采用传统的极限平衡法，对于岩质边坡难以合理判定坡体的松弛区域、滑动面位置、及确定结构面抗剪强度参数，总之，对岩质边坡的稳定性分析存在一定局限性[2]。

而采用强度折减法对岩质边坡的稳定性分析可以取得理想的效果。早期郑颖人等[3]，赵尚毅等[4-6]采用强度折减法对岩质边坡变形破坏机制进行了研究分析，并证明方法的可行性。许多学者[7-13]结合此方法对岩质边坡稳定性评价开展了进一步研究，如李大茂等[7]对全强风化岩质边坡失稳破坏机制进行了研究。卜林等[8]对含软弱结构面岩坡稳定性进行了分析。江学良等[9]对层状岩质边坡开挖过程的岩体的变形和应力状态及屈服状态进行了模拟分析，皆取得了一定成果。该方法通过对岩土体的物理力学参数进行折减，直至结构达到极限状态，即为边坡的安全系数[14]。结果可以反映出岩质边坡的松弛区域，判定边坡的潜在滑移面，为岩质边坡的稳定性分析提供有力的判断依据。

本文以长沙某矿坑顺层岩质边坡为研究对象，利用强度折减法的有限元数值分析软件Phase2对顺层岩质边坡潜在变形破坏模式与支护稳定性进行分析。文中对岩质边坡稳定性的分析方法、步骤和结果可为类似工程边坡的稳定性评价提供借鉴。

1 强度折减法计算原理

强度折减法最早是Zienkiewize在二十世纪七十年代提出运用计算，结合有限元分析手段，采用降低岩土强度的方法来计算边坡的安全系数，对边坡稳定性进行评价。

在理想的弹塑性有限元计算中，按照一定的强度准则判断岩土体的屈服破坏情况，从岩土体实际的物理力学性状出发，将边坡的岩土体强度参数黏聚力c和内摩擦角φ以系数F进行折减，如下所示：

c′=c/Fs

(1)

φ′=arctan(tanφ/Fs)

(2)

将c′和φ′带入程序中计算，直至边坡达到极限平衡状态，发生失稳破坏，破坏时对应的折减系数Fs本质上即为边坡的传统意义上的稳定性系数，其代表实际工程岩土体的安全稳定程度。

有限元强度折减法考虑了岩土体内部的应力应变关系，可对任意几何形状或不均匀材料的边坡开展分析，因而此计算方法可得到更接近实际情况的危险滑移面及相应的稳定性系数，同时具有可根据塑性区的逐步发展观察边坡的渐进破坏过程等诸多优点[14]。

本文岩土体材料的本构模型按照理想的弹塑性模型考虑，采用摩尔-库仑的强度屈服准则，运用有限元数值模拟分析软件Phase2，基于强度折减法计算原理的方法，来求解岩质边坡的稳定性系数。

2 边坡计算模型与参数

工点边坡位于长沙某矿坑，该段边坡坡面裸露，坡长约25 m，坡高35 m～39 m，坡顶有植被覆盖，边坡总体倾向211°，坡面上部(距坡脚24 m以上)坡角73°～76°，下部坡角55°～60°，无支护，无地表水及地下水渗出，坡面上无溶蚀沟槽，坡脚有采空区，宽度约10 m，节理裂隙发育，层理面明显，容易发生顺层滑移破坏，见图1。

图1现状边坡影像图

边坡岩体类型为Ⅲ类，主要受两组裂隙控制，裂隙L1和裂隙L2结构面较粗糙，张开度1 mm～2 mm，局部钙质胶结，延伸长度5 m～8 m。结构面结合程度差，属硬性结构面。产状分别为355°∠-53.4°和92°∠-40.0°。岩层层面为外倾结构面，边坡层面产状为210°∠48°，该段边坡可能产生沿岩层层面顺层滑移；裂隙L1、裂隙L2与边坡大角度相交内倾，对边坡稳定性影响小。裂隙与层面在软件中按节理进行定义模拟，结果见图2。

图2边坡工程地质模型图

边坡从上到下岩土层分别为人工填土、黏土层及微风化泥灰岩，对应岩土物理力学参数如表1所示。

结合现场踏勘调查及设计规划资料，如图1中所示，该段边坡坡顶为水泥厂厂房，后期将在该处建设游乐场建筑物，且坡脚为采空区。该段边坡周边环境显得较为复杂，故如何成功治理该段边坡显得十分重要。

表1 岩土物理力学参数

3 数值模拟结果分析

本工点数值模拟边坡治理过程的主要思路是：(1) 采用Phase2软件模拟原状矿坑场地开挖工况，判断现状边坡应力松弛区域；(2) 根据现状边坡稳定状态，推断其安全系数，并反演松弛区域层面与结构面参数；(3) 进行刷方卸载及施加锚固工程，使之安全系数满足现行规范要求≥1.35。

3.1 边坡应力松弛区判定

采用数值模拟Phase2软件，分11步对原状矿坑场地开挖至现状边坡状态，对比现状边坡与原状场地主应力变化情况。

在分析边坡的稳定性时，假定采空区不存在，仅对采空区上部岩土层进行稳定性分析。数值模拟结果见图3所示，该边坡应力松弛区较为集中的区域，集中在边坡上部及坡脚平台外侧向下部区域。该边坡应力集中区域，集中在边坡坡脚下部。

图3现状边坡应力松弛区分布图

提取图3中1、2号直线的应力σ1变化量数值。以2号线为例，分布曲线如图4所示。2#线的应力松弛区可分为两段：0～18 m为应力松弛显著区，18 m～32 m为应力松弛渐变区，32 m之后应力基本不变。同样可得，1号线的应力松弛区可分为两段：0～25 m为应力松弛显著区，25 m～65 m为应力松弛渐变区，65 m之后应力基本不变。

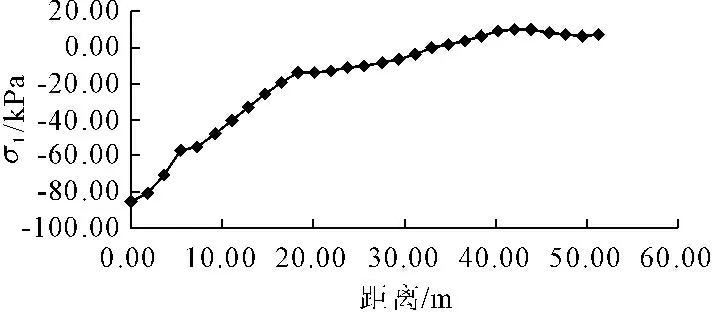
图4 3断面边坡2号线Δσ1曲线图

3.2 边坡潜在变形破坏模式分析

根据现场调查情况及勘察设计资料，初步判定该段边坡处于基本稳定状态。按现状边坡处于基本稳定，即稳定性系数为1.10左右对结构面参数进行数值反演[15]。

模拟过程，结构面参数按照表1参数进行折减计算直至接近1.10为止，数值模拟结果如图5所示，计算结果显示边坡稳定性系数为1.09。反演主要结构面参数见表2所示。

图5 3断面边坡潜在破坏模式(总位移云图)

岩质边坡潜在破坏模式为沿顺倾岩层层面滑移-弯曲破坏。结果与张倬元等[16]提出的岩体变形破坏地质力学基本模式一致。

结合边坡自然坡率、岩层产状，有限元数值模拟边坡松弛区结果，边坡现状变形状态分布，及工程经验对主断面进行综合分析，并判定潜在滑动面位置，如图5所示。

3.3 支护稳定性评价

参照数值模拟边坡现状可能发生的破坏模式和潜在滑动面，对边坡进行加固处理。由于本工点边坡破坏模式主要为沿顺层滑移-弯曲破坏，潜在滑动面位于坡体向内10 m范围内，故选择预应力锚杆进行加固支护，采用系统锚杆对浅表层岩体进行辅助加固，预应力锚杆的锚固段应深入至潜在滑面之下。

确定治理方案如下：对边坡岩土体按照1∶0.5进行浅层刷方；预应力锚杆设计长度15 m，锚固长度5 m，垂直间距4 m，设计荷载250 kN；系统锚杆长度5 m，抗拉强度50 kN。

数值模拟结果见图6～图8，治理之后，边坡稳定性系数为1.71。支护前边坡最大变形为142 mm，支护后边坡最大变形为6 mm，比支护前减少了95.8%。可见，在增加预应力锚杆等措施治理之后，有效的控制了坡体的滑移变形。

图6 3断面边坡潜在破坏模式(总位移云图)

图6为主断面边坡治理后的总位移云图，由图6可见，边坡潜在滑动面明显向深部转移，治理措施效果十分明显。

图7 3断面边坡现状塑性区分布云图

图8 3断面边坡加固后塑性区分布削减云图

图7、图8为边坡治理前后塑性分布区云图，由两图对比可知，治理之后的边坡塑性屈服变形明显改善，加固后的边坡处于稳定状态。

3.4 极限平衡法计算与对比验证

用极限平衡软件Slide对现状边坡与加固后的边坡进行计算。结合判定的潜在滑动面，在模型中定义5 cm的滑动带薄层，用指定非圆弧滑面进行计算，对现状边坡按照稳定性系数1.10左右进行反算。

计算结果如表3所示，边坡治理后稳定性系数Fs=1.392，满足《建筑边坡工程技术规范》[15](GB 50330—2013)稳定安全系数≥1.35的要求。通过极限平衡法的计算，进一步验证支护方案有效性。

表3 数值计算和极限平衡计算结果对比

4 结 论

本文基于数值仿真技术，采用强度折减安全系数的非线性有限元数值极限分析法，对长沙某矿坑顺层岩质边坡潜在变形破坏模式与支护稳定性进行分析评价。分析了矿坑岩质边坡的应力松弛变化特征，根据现场变形迹象与数值模拟结果判定岩质边坡潜在变形破坏模式，选择合理支护措施进行边坡治理，并对其支护后边坡稳定性进行分析评价，最后结合极限平衡软件Slide进一步验证支护的有效性。