高埋深隧洞岩爆预测数值方法适用性研究
2018-08-21王浏刘郭晓利
于 茂 王浏刘 郭晓利
岩爆是高地应力条件下硬岩开挖卸荷过程中常常伴随发生的岩体破坏模式,是一种具有空间和时间随机性的突发性地质灾害问题。岩爆的发生与地质因素、工程环境因素、地下水以及人为施工开挖方式等均有较大关系。由于岩爆的显著危害性,且目前岩爆发生机制不完全清楚,国内外许多学者对岩爆及其岩石失稳理论展开研究,其中具有代表性的理论包括强度理论、能量理论、刚度冲击理论、损伤理论、分形理论和突变理论等[1]。同时,数值模拟逐渐成为一种解决岩爆预测问题的有效手段,并催生了一些具有代表性的硬岩脆性破坏模型。如Hajiabdolmajid[2]等基于M-C模型提出了黏聚力弱化–摩擦力强化模型(CWFS模型);Edelbro等[3]提出了可用于模拟围岩脆性破坏范围的CSFH模型;Martin[4]等基于Hoek-Brown准则提出的m-0准则等。国内学者中有江权等[5]提出的硬岩劣化本构模型RDM、黄书岭等[6]提出的广义多轴应变能强度准则GPSE等。唐春安等[7-8]基于自行开发的有限元分析软件RFPA开展了一系列的数值试验,分析了岩爆过程中岩石的真实破裂过程及声发射现象。
目前,依据理论性的岩爆预测方法和判据仅可对岩爆发生的可能性及等级进行评判,无法给出岩爆的破坏区域和深度。而在高埋深隧洞的实际支护设计与施工中,更关注的是洞周围岩的破坏模式及深度,其对开挖方式、支护类型、支护时机等的相关设计更具指导意义。因此,本文采用弹性模型、理想弹塑性模型、弹脆塑性模型、m-0准则及CSFH模型等,对比分析了各本构模型的适用性,结合工程实例进一步分析了高埋深隧洞的岩爆特性及破坏特征。
1 硬岩脆性破坏本构模型
1.1 理想弹塑性
M-C屈服准则认为当材料内部点的剪应力达到该点的抗剪强度时,该点即发生破坏,剪切强度与作用在该点的正应力呈线性关系。M-C屈服准则可以写为:
式中 τ——正应力作用下的极限剪应力;
c——黏聚力;
φ——内摩擦角。
1.2 m-0准则
Hoek-Brown准则中极限主应力的表达式为:

式中 σ1——破坏时的最大主应力;
σ3——作用于岩石试件上的最小主应力;
σc——完整岩石的单轴抗压强度;
mb——经验参数值;
s、a——与岩体特征有关的常数。
Martin在硬岩脆性破坏的研究过程中发现,当Hoek-Brown准则中的经验参数mb取0,岩体特征常数s取为0.112时,利用Hoek-Brown准则可较好地预测脆性岩体的破坏位置及破坏深度,进而在此研究的基础上,提出了m-0准则。该准则认为岩体发生脆性破坏,主要是黏聚力丢失所致,摩擦角在脆性破坏过程中并未被激发,其作用可忽略。m-0准则的极限主应力表达式为:
σ1-σ3=Aσc
式中, A=sa,对于硬岩,a一般取为0.5,而s通常取为0.112。
1.3 CWFS模型
CWFS模型是在Mohr-Coulomb基础上发展起来的。Hajiabdolmajid在研究ACEL Mine-by试验隧道Lac du Bonnet花岗岩的脆性破坏后,提出了可考虑岩石脆性破坏过程中材料力学性能变化的CWFS模型。该模型假定,在岩石破损的初始阶段,由于微裂纹的增多,岩体内部微观颗粒相互之间的束缚作用逐渐减小或失去,表现为岩体黏聚力逐渐减小。岩体内出现裂纹后,在裂纹面上法向力和剪切力的共同作用下,裂纹面上的摩擦力逐渐发挥作用,随着裂纹的发展、贯通,摩擦强度不断增大。当岩体强度达到峰值、产生一定塑性变形时,摩擦强度发展到其最大值,而岩体的粘结强度则会经历一个快速下降的过程。黏聚力和摩擦强度分量在经历不同的塑性变形(0.2%和0.5%)后分别达到各自的残余强度。
1.4 CSFH模型
Edelbro[3]在深入研究GSI大于75的较为完整岩体的破坏范围后,采用交叉剪切带的深度作为岩体破坏的评判标准,提出了瞬时粘结软化-摩擦硬化模型(CSFH)。在CSFH模型中,考虑岩体一般存在微裂隙等缺陷,一般将岩体的初始摩擦角设为10°(即φpeak=10°),残余摩擦角取为Mohr-Coulomb准则中岩体的内摩擦角(φres=φm);岩体的残余黏聚力一般取为Mohr-Coulomb准则中岩体黏聚力的0.3倍,即有cres=0.3cm,而岩体黏聚力的峰值强度cpeak可以利用Mohr-Coulomb准则式(1)计算得到,具体的计算公式为:
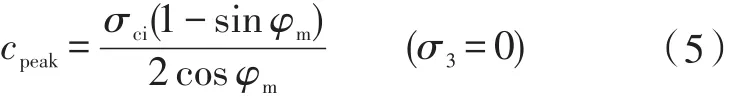
式中 σci——完整岩块的单轴抗压强度。
CSFH模型中“黏聚力的弱化和摩擦角的强化”为瞬时发生,因此,该模型也带有弹-脆塑性模型的特点。
2 计算模型
Mine-by试验隧道是加拿大原子能有限公司(ACEL)于1990—1995年间在其地下研究实验室进行矿用试验时,在Lac du Bonnet花岗岩体中开挖的一条直径3.5 m、长46 m的圆形试验隧道。试验隧道在开挖过程中为减小对原岩的扰动,开挖的循环进尺仅为0.5~1 m,且采用非爆破的排钻技术及机械破碎开挖技术开挖。Mine-by试验隧道沿中主应力 σ2(45±4 MPa)方向开挖,初始最大主应力 σ1和最小主应力 σ3分别为(60±3)MPa和(11±2)MPa。两个方向最大应力比接近于6∶1,开挖加剧了隧道顶部、底部的应力集中,试验隧道开挖后,围岩发生持续性剥落,最终形成了如图1所示的V字形破坏坑(实测破坏坑深度约0.525 m)。
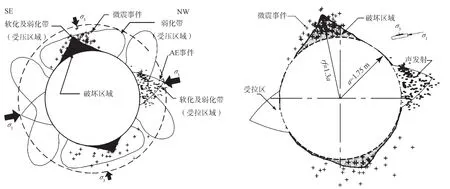
图1 ACEL Mine-by Experiment试验隧道围岩破坏特征
Mine-by试验隧道所在Lac du Bonnet花岗岩的岩块参数、岩体力学指标等见表1。
3 不同本构模型的岩爆预测结果对比
3.1 岩爆破坏特征对比
为对比分析不同本构模型下洞壁岩爆破坏特性及模式,本文采用理想弹塑性模型、CWFS模型、CSFH模型、基于Hoek-Brown模型的m-0强度准则对Mine-by试验中Lac du Bonnet花岗岩隧道的卸荷岩爆进行数值模拟。下面给出各种模型的数值计算结果及其结果分析。
如图2所示,各数值模型均能预测侧拱处的张拉破坏区,弹性模型采用强度系数(岩体强度与所受主应力的比值)进行预测,其余模型采用张拉破坏区预测。而各模型对洞顶附近的V形剪切破坏区域的发生位置及深度的预测结果有明显区别:(1)弹性模型基本无法预测V形破坏区域;(2)由于理想塑性模型无法考虑岩体受扰动后材料劣化过程,M-C模型洞顶附近V形剪切破坏区深度为0.146 m,约为实际破坏深度的1/3;(3)m-0模型计算得到的V形破坏区深度为0.546 m,与实际的破坏深度相差4%;(4)CWFS模型计算所得V形破坏区深度为0.544 m,与实际的破坏深度相差3.6%;(5)CSFH模型计算得到的围岩V形破坏深度为0.535 m,与实际的破坏深度相差1.9%。
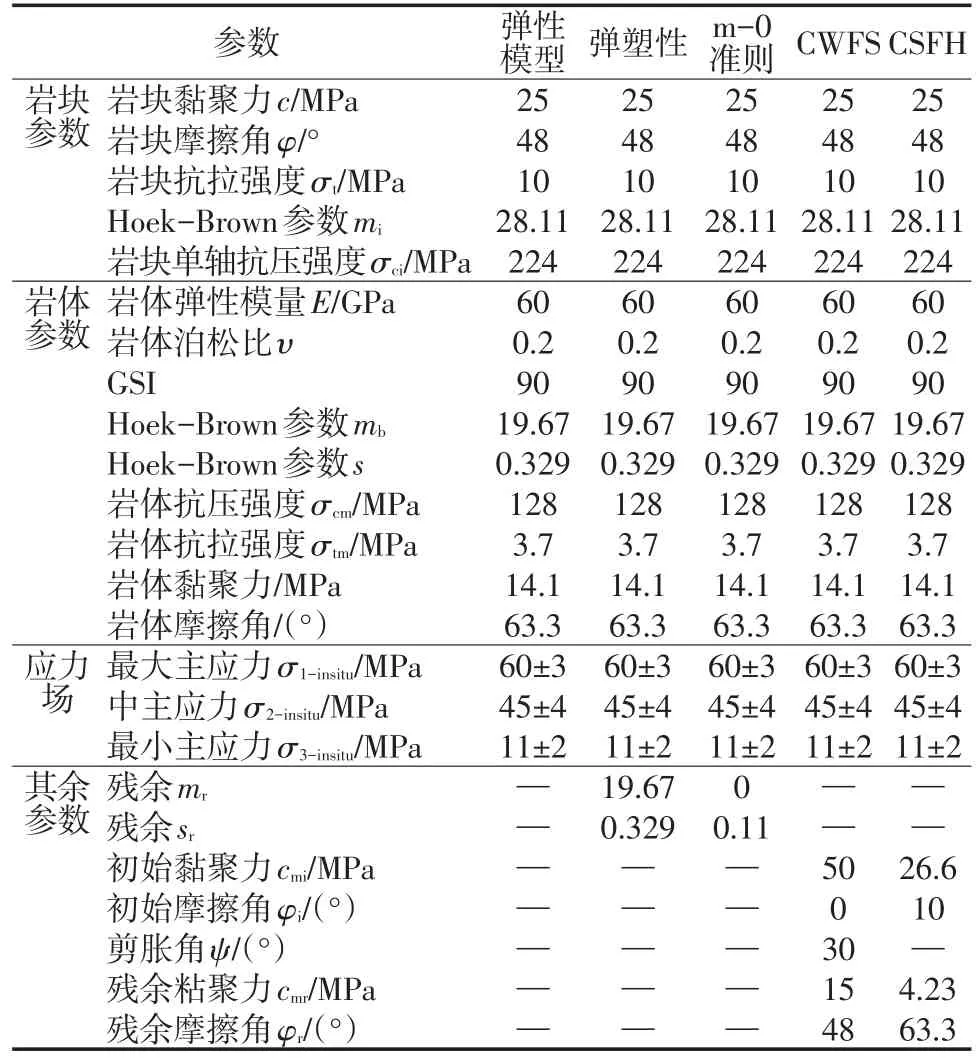
表1 Lac du Bonnet花岗岩物理力学参数[2,3]
3.2 数值模型适用性探讨
从数值模拟实验结果来看,弹性模型和理想弹塑性模型的岩爆预测结果不理想,这2种模型不适用于岩爆预测。而CWFS模型、CSFH模型及m-0准则预测的围岩破坏位置和破坏范围与现场实验结果基本一致,其中CWFS模型的剪切带分布与实际观测结果接近。但CWFS模型及CSFH模型的计算参数如初始摩擦角、初始黏聚力、残余摩擦角、残余黏聚力及相应的塑性应变值需获取包含下降段的应力应变全过程曲线,而难以通过常规试验得到,因此在工程应用方面较受限制。而采用基于Hoek-Brown模型的m-0准则,基于地质勘察得到的GSI指标体系,即可确定本构模型中的所有参数,从而快速进行高埋深硬岩隧洞的岩爆预测,是目前解决工程岩爆问题的有效数值模拟手段。
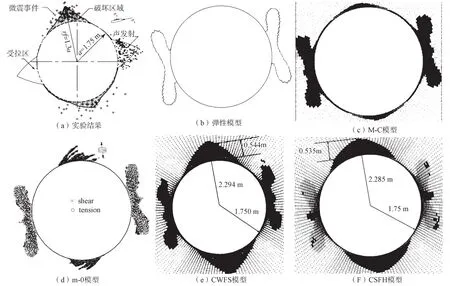
图2 各数值模型的岩爆预测结果对比
4 结 语
本文针对高埋深硬岩隧洞的岩爆预测问题,对隧洞开挖卸荷扰动下岩石的岩爆破坏机理及模式进行了探究。结合现场观测结果,采用多种硬岩脆性破坏准则,对比研究了Mine-by试验隧道在高地应力条件下的破坏机理。研究结果表明,CWFS模型、CSFH模型和m-0准则在高埋深隧洞的岩爆预测方面效果较好,数值模拟结果与实际情形基本一致。但采用基于Hoek-Brown模型的m-0准则,更便于地质GSI参数与计算参数的转化,进而判定洞室岩爆发生区域及破坏特征,该数值算法为深埋隧洞工程设计及施工过程安全提供了相关技术支撑。
