基于滑转率的双电机双轴驱动车辆转矩协调分配

2018-08-21武仲斌迟瑞娟杜岳峰毛恩荣

农业工程学报 2018年15期

武仲斌，谢斌，迟瑞娟，杜岳峰，毛恩荣

（中国农业大学现代农业装备优化设计北京市重点实验室，北京 100083）

0 引言

电动车辆动力传动系统与整车性能密切相关，其结构及工作模式直接影响整车动力性、经济性及行驶稳定性等多项性能。其中，采用四轮驱动方案将驱动力总需求分配至前、后轴，改善轮胎附着状况，有利于提升车辆牵引力及稳定性。作为电驱动车辆特有的四驱结构之一，双电机前后轴独立驱动型式（下称双电机双轴驱动）将 2台驱动电机分散布置在前、后驱动桥输入端或集成到驱动桥内部形成电动车桥[1-3]，传动路线短，传动效率高，且可通过主动调节前后驱动电机之间的动力分配，改变车辆运动行为，提升车辆动力学性能。

在双电机转矩分配方面，Mutoh等[4-6]对双电机双轴驱动车辆电机转矩分配策略做了一定的研究，其考虑到了垂直载荷与附着力的关系及加减速对前、后轴载荷的影响，并提出根据前后轴载荷比主动调节前、后电机的转矩分配关系，从而使转矩更多地转移至垂直载荷较大的驱动轴，一定程度上改善了车轮滑转情况，但在分配转矩时未考虑路面条件，故对附着较差的情形即使垂直载荷较大，仍可能造成驱动轮滑转；范晶晶等[7-9]将双轴独立电驱动结构扩展到多轴，提出分层控制的思路，在上层中根据轴荷比分配各轴电机转矩，在下层中监控各轴实际滑转率并在必要时直接限制滑转轴的驱动转矩，这实际是一种被动控制，且对未滑转轴的附着条件利用不充分；Hyeongcheol等提出了以前、后轴理想转速差为控制目标的主动转矩分配策略[10-11]，在对接路面上对滑转率的抑制作用明显，但在处理均一低附着、对开路面时，与滑转轴直接限制方式相比，效果较差。在驱动防滑控制方面， Fujii等[12]充分利用电机驱动系统自身动力学特性，提出了一种避开车速测量的滑转率实时估计方法；张利鹏等[13]则利用驱动电机转矩可精确估算的特性，提出了一种基于电机输出特性的最佳滑转率识别方法，并以试验验证了其在驱动防滑控制中的可行性；冯彦彪等[14-15]针对一定作业环境下的特种车辆，分别设计了基于模糊规则和 PID的轮胎滑转率控制器，但均属被动控制。

针对双电机双轴驱动车辆的转矩分配问题，本文以抑制车轮过度滑转、提升整车牵引力为目标，基于“附着系数-纵向滑转率”关系，将面向牵引力控制的转矩分配问题归结为对纵向滑转率的控制。综合考虑直行及转弯工况下各个车轮的滑转情况，提出了一种将单轴滑转率最优控制与轴间转速差控制相结合的主动转矩分配策略，并在Matlab/Simulink软件以及dSPACE半实物仿真平台上对控制策略进行了验证。

1 整车动力学建模

1.1 车体动力学模型

车辆行驶在水平路面上，忽略滚动阻力、空气阻力时，考虑纵向、侧向、横摆以及 4个车轮转动，建立用于转矩分配控制器设计的七自由度动力学模型[16-17]如下。

纵向运动

式中m为整车质量，kg；Iveh、Jw分别为整车及车轮转动惯量，kg·m2；δ为轮胎转向角，rad；u,v分别为车辆纵向速度及侧向速度，m/s；γ、ωi分别为车身横摆角速度及各车轮转动角速度，rad/s；a，b，Bw，rw分别为质心到前、后轴的距离、轮距及车轮滚动半径，m；Mdi为作用于车轮上的驱动转矩，N·m；Fxi、Fyi分别为地面对车轮的纵向及侧向反力，N；i = 1,2,3,4,分别代指左前、右前、左后及右后车轮。

按照高选原则，将左右两侧车轮转动方程等效至轴中点处，并将轮边驱动转矩换算成电机输出转矩，如式（5）、（6）所示。

式中ω1，ω2，ω3，ω4分别表示左前、右前、左后及右后4个车轮的转速，rad/s；ωfc，ωrc分别为前、后轴中点处等效旋转角速度，rad/s；Fxf，Fxr分别为前、后轴受到的地面纵向反力，N；Tmf及Tm分别为分配至前电机的驱动转矩和总驱动转矩，N·m；it及ηt为传动系统总速比和效率。

1.2 非线性轮胎模型

为准确反映轮胎动力学特性，本文采用Pacejka魔术公式[18-19]描述轮胎的非线性动力学行为，其统一表达式如式（7）所示。

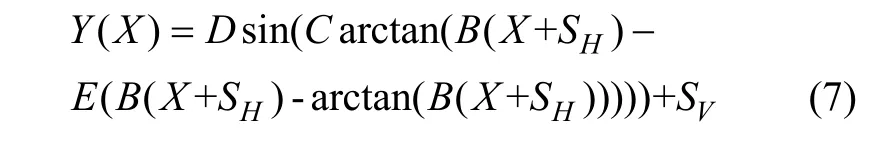
式中Y为纵向力或侧向力，N；X为轮胎纵向滑转率或侧偏角，rad；B、C、D、E分别为拟合曲线的刚度因子、形状因子、峰值因子和曲率因子，SH、SV分别为曲线的水平、垂直偏移常数，均取0。

因此，在计算纯驱动工况的轮胎纵向力Fx0时，有

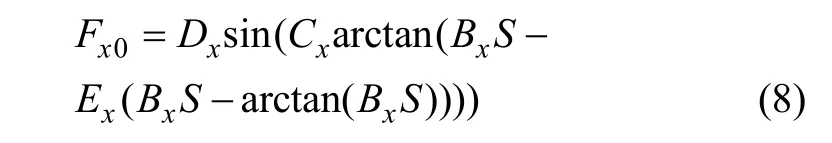
其中，

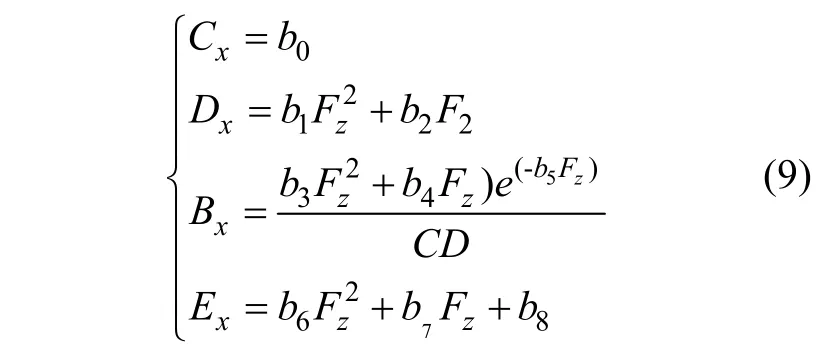
在计算纯转弯工况的轮胎侧向力Fy0时，有

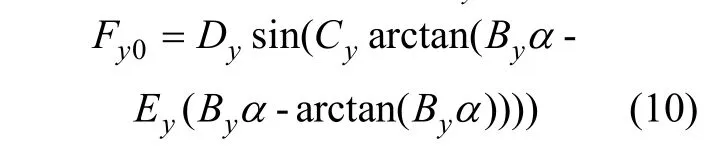
其中

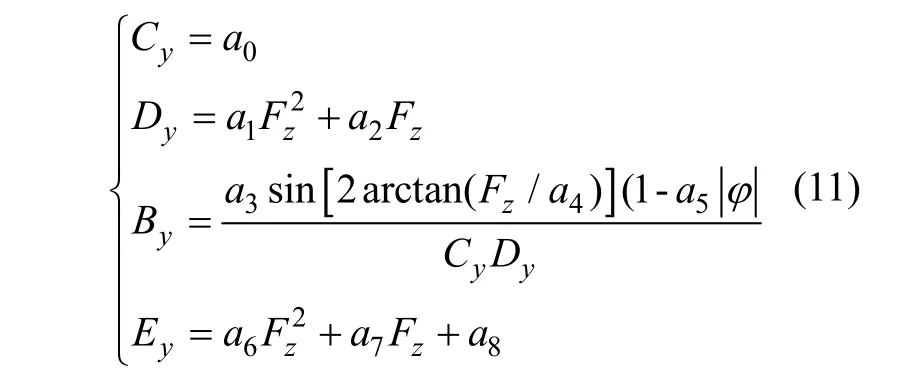
式中a0～a8，b0～b8为拟合参数，取值见表1；Fz为轮胎垂直载荷，N；α、φ分别为轮胎侧偏角和侧倾角[20]，rad；S为轮胎滑转率。

在驱动和转向的联合工况下，轮胎同时承受纵向力和侧向力，受“附着椭圆”条件的约束，最终轮胎力的表达式为

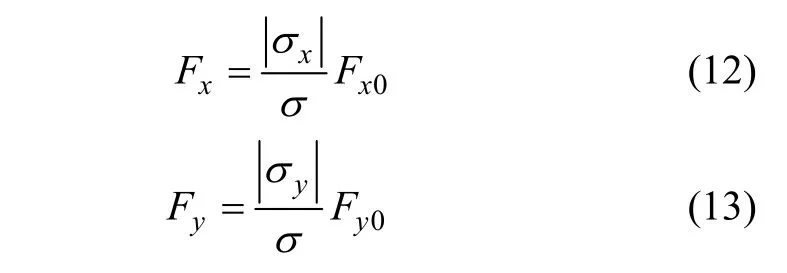
式中Fx、Fy分别为联合工况下的轮胎纵向力和侧向力，N，并且，

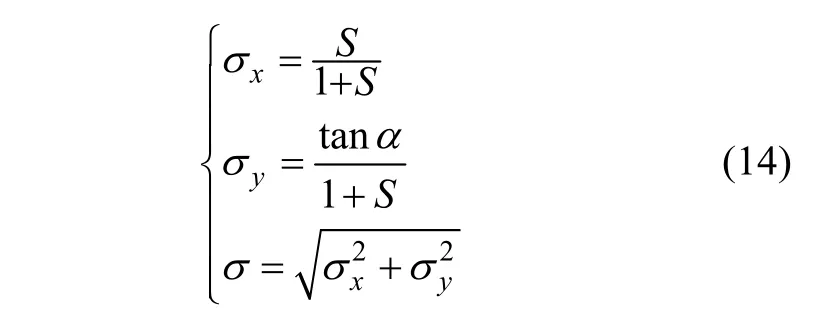
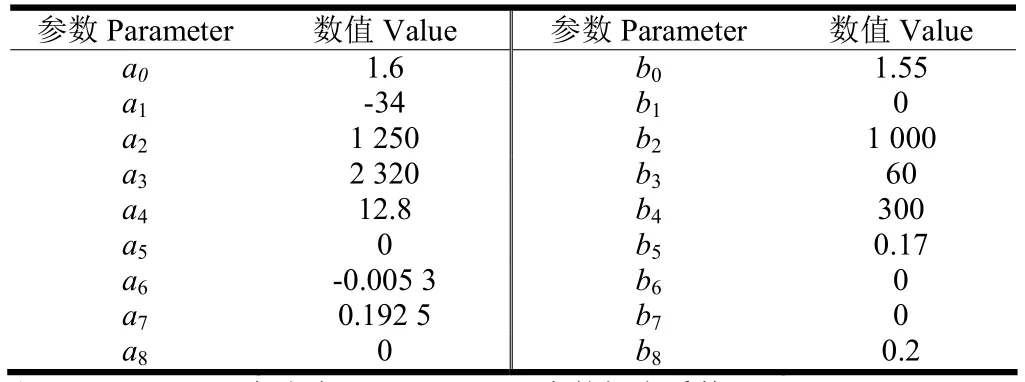
表1 魔术公式轮胎模型参数Table 1 Parameter values of tire model using magic formula

2 控制策略的制定

2.1 控制系统总体结构

本文所讨论的问题可描述为：加速踏板行程决定期望总驱动转矩，以该转矩为约束（上限），如何分配前、后电机输出转矩，以使前后轴不发生过度滑转，即处在稳定附着区[21-22]。将转矩分配控制系统分为上、下2个层次，如图1所示。上层以前、后轴最优滑转率为目标，根据车辆实时反馈回的前后轴实际滑转率等状态信息，由滑模控制器分别给出前、后电机预分配转矩及驱动总转矩，并在总转矩后端引入一饱和环节，以考虑驾驶员期望转矩的限制；下层以前后轴理想转速差为目标，根据车辆实时反馈的前后轴实际转速差等状态，由滑模控制器首先计算出最终分配至前电机的转矩，并结合上层给出的总转矩，得到最终分配至后电机的转矩。

图1 转矩分配控制系统结构Fig.1 Sketch diagram of control system for torque distribution

2.2 控制策略上层-可分配驱动总转矩计算

根据车轮转动方程式（5）、（6），过大的驱动转矩会引起车轮的过度滑转，导致车辆偏离附着稳定区；而驱动转矩过小时，轮胎滑转率也低，势必造成对路面附着条件利用的不充分。暂不考虑驾驶员期望，驱动总转矩应为能使前、后驱动轴实际滑转率均维持在最优滑转率时前、后电机驱动转矩之和，为此，需根据前、后轴实际滑转率和当前路面附着条件，分别计算前、后轴最大驱动转矩。首先考虑前轴并记其滑转率为Sfc，根据滑转率定义

式中ufc为前轴中心处的等效车速，m/s。

对式（15）求导，有

考虑车辆转弯时的情形，当车轮转角δ不大时，求得

式（16）中车速ufc及其一阶导数如下

又车体作平面运动时，满足如下运动学关系

将式（3）、（19）及（20）代入式（18），有

将式（5）、（21）代入式（16），得到转弯工况下关于前轴滑转率Sfc的一阶微分方程，如式（22）。

考虑采用滑模控制算法对前轴滑转率进行控制，在被控对象也即式（22）中，控制量为Tmf，也即前轴电机转矩。加速度ax、ay，横摆角速度γ以及转速ωfc等状态参数可通过加速度计、陀螺仪以及编码器测取。横摆力矩Myaw可通过轮胎模型计算出的轮胎力间接得到。质心速度u、v很难直接测取，通常由相应的参数估计算法[10]得到。

因被控对象式（22）为一阶系统，故设计前轴滑转率最优控制滑模面mSf为前轴实际滑转率Sfc与前轴最优滑转率Sf_opt的偏差[23]eSf，即

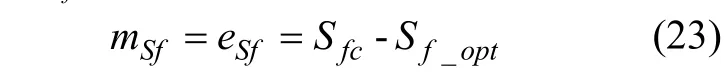
根据滑模可达性条件[13]，采用指数趋近律，设计得到前轴驱动电机控制律为

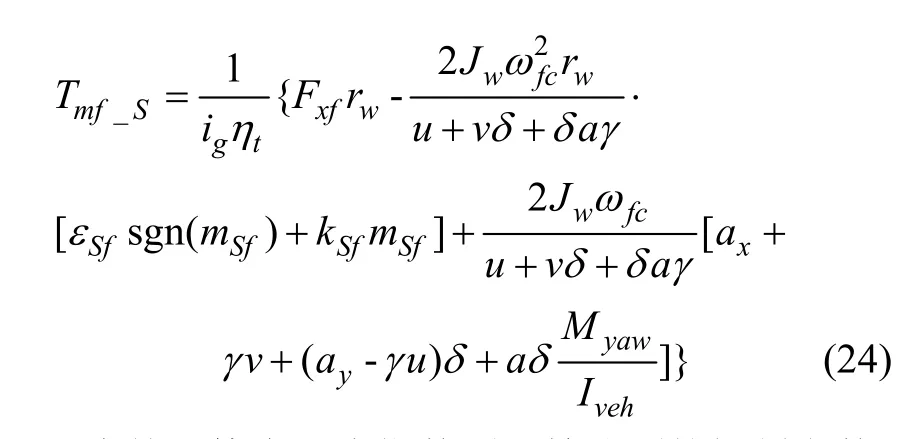
式中εSf和kSf为趋近律中对应指数项和等速项的控制参数，影响前轴滑转率趋向最优滑转率时的速度。sgn(mSf)为关于滑模面mSf的符号函数。

联合式（22）、（23），可证明上式给出的控制律能保证所定义的滑模面可达[24]，即为了进一步减弱控制输入的高频抖动[25]，考虑用连续函数θ(mSf)替代符号函数sgn(mSf)，定义为

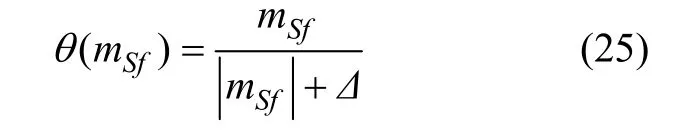
式中Δ是滑模面边界层厚度，为很小的正常数。

因此，由转矩分配控制策略上层计算得到的前电机预分配转矩如式（26）。

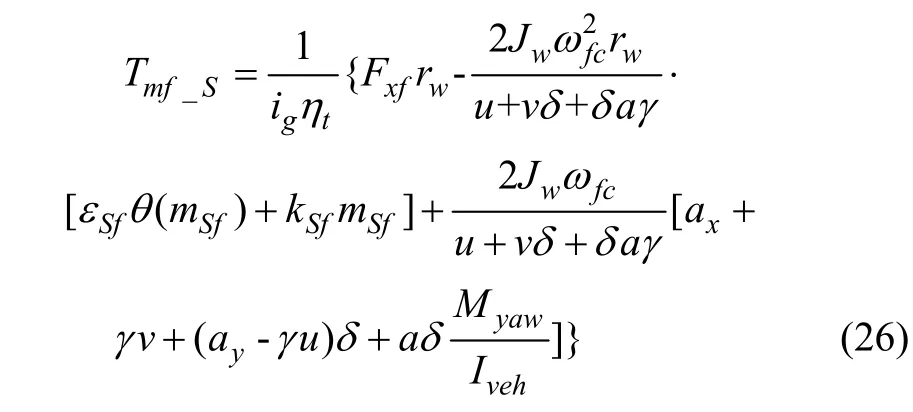
对于直行工况，即δ=0时，式（26）变为

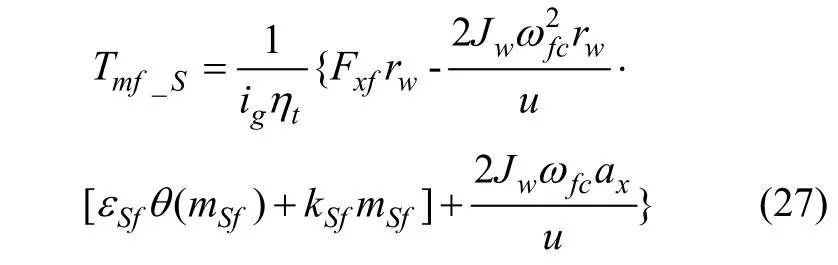
由于后轴两侧车轮在任何情况下都不会发生偏转，因此，后电机预分配转矩表达式在形式上与式（27）给出的前轴电机在直行工况下的表达形式一致，则

式中Tmr_S为控制策略上层给出的后电机预分配转矩，εSr和kSr分别为趋近律中等速趋近项和指数趋近项系数，影响后轴滑转率趋向最优滑转率时的速度。

不考虑驾驶员需求的约束时，可供下层分配的驱动总转矩Tdst为前、后电机预分配转矩之和，即

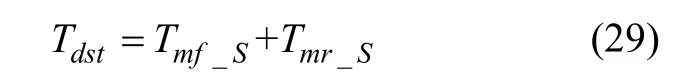
进一步考虑驾驶员期望的约束，即在任何时候由控制律计算出的驱动总转矩绝不应超过由加速踏板行程解析出的驾驶员期望转矩，因此，综合滑转率最优控制和驾驶员期望，最终得到可供下层分配的驱动总转矩Tlmt为

式中Treq为驾驶员期望转矩。Tlmt实质上给出了在不超越驾驶员意志、并且确保车辆处于稳定附着区的前提下，使车辆整体滑转率最逼近最优滑转率时的驱动总转矩，也是使各轮滑转率的均值趋于最优滑转率的必要条件。

2.3 控制策略下层-驱动转矩分配控制

假设前、后轴的最优滑转率是一致的，若以前、后轴滑转率相等为目标分配上层基于最优滑转率计算出的驱动总转矩时，可使前、后轴滑转率共同趋于最优滑转率。考虑到前、后轴车速一致或接近，在实际控制时，前、后轴等滑转率控制可简化为转速差闭环控制。特别地，在转速差闭环控制中，前、后轴转速本身是开环的，因而在前、后轴之间不会产生循环功率。记前、后轴实际转速差及目标转速差分别为Δωfr和Δωfr*，则实际转速差与目标转速差的偏差eω及其导数分别为

采用滑模控制算法时，设计滑模面mω

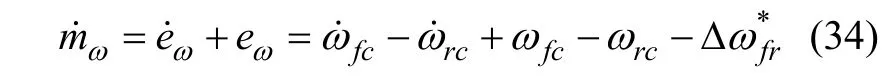
将式（5）、（6）代入式（34），并将总驱动转矩Tm更换为可分配的驱动总转矩Tlmt

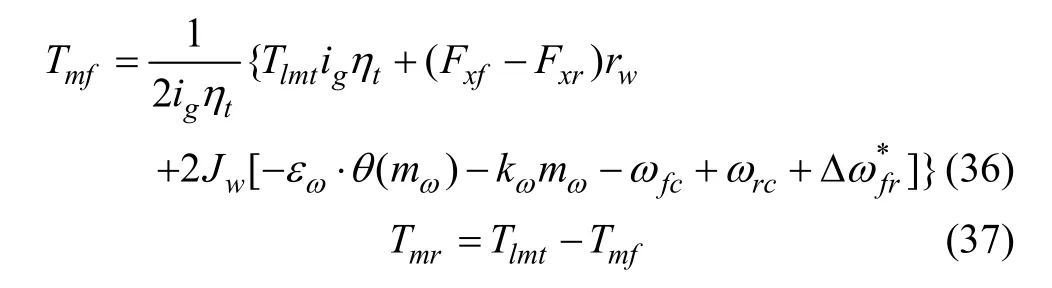
式中Tmf及Tmr分别为分配至前、后电机的转矩，N·m；εω、kω分别为趋近律中等速趋近项和指数趋近项系数。

考虑车辆转向时前、后轴理想转速的差异，忽略轮胎侧偏特性，且假设前、后轴均处于纯滚动状态，则前、后轴理想转速差Δωfr*可由图3求得

显然，当前轮偏角较小时，目标转速差可近似为零。将式（38）代入式（36）、（37），得到最终的前、后轴电机转矩分配律，如式（39）、（40）所示。式中Tlmt由式（30）给出。

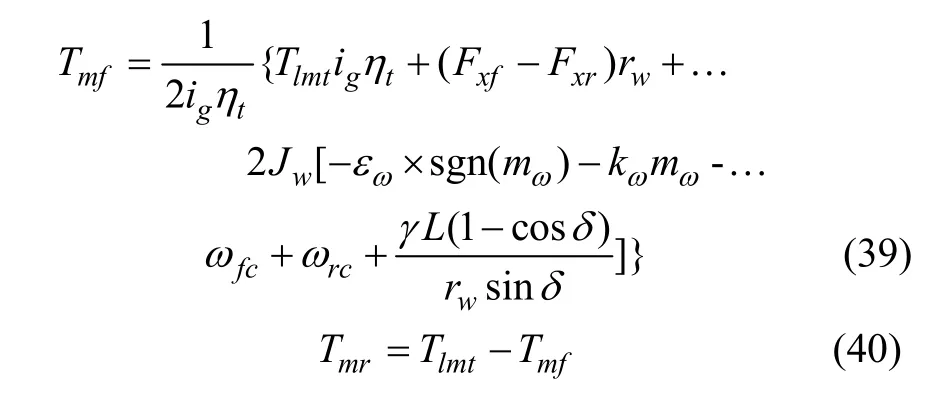
图2 2轮车辆模型转向示意图Fig.2 Steering diagram of two-wheeled vehicle model

3 仿真验证

为验证提出的控制策略，基于Matlab/Simulink平台，搭建了转矩分配控制模型及整车动力学模型，如图 3所示。

其中，电机模型被等效为一阶惯性环节[26]。在仿真计算时，分别对直行和转弯两类工况下车轮滑转率的控制效果进行分析，并且，在直行时取附着系数分离路面和高低附着对接路面两种路况进行仿真，转弯时则取低附着路面上的移线工况进行计算。为说明控制效果，在对转矩主动分配控制仿真的同时，对平均分配时[27]的控制效果也进行了对比分析。车辆基本参数及控制器参数按表2选取。

Solenostoma duthiana Steph.刘胜祥等（1999）（36）大萼管口苔（大萼叶苔）Solenostoma macrocarpum（Schiffn.ex Steph.）Vana

图3 基于Matlab/Simulink的控制器模型在环仿真Fig.3 Controller-model in-loop simulation based on Matlab/Simulink

表2 仿真车辆基本参数及控制参数Table 2 Basic parameters of vehicle simulated and control parameters

3.1 附着系数分离路面直线加速

对于左右侧轮胎附着系数分离路面，前后轴均为低附着。取各轮附着系数 μ左前=μ左后=0.3, μ右前=μ右后=0.8，驾驶员期望转矩300 N·m，车辆由原地起步加速8 s，电机输出转矩和纵向车速、左侧以及右侧轮胎滑转率的仿真结果分别如图4a、4b以及4c所示：转矩平均分配时，前后电机均按150 N·m输出转矩，因左侧附着系数低，故左前轮及左后轮滑转率在加速一开始便很快超过 70%并始终维持在70%到80%之间，在8 s时纵向速度达到24.5 m/s；转矩主动分配时，驾驶员期望转矩受到限制，前、后电机输出转矩分别在124和106 N·m附近，左侧车轮滑转率被控制在最优滑转率0.12附近，而车辆末速度与等比分配时基本相同，这主要是由于低附着路面的“纵向附着系数-滑转率曲线”极为平缓”所致，也即对于低附着路面，转矩主动分配策略对牵引力提升并不明显，但可有效抑制车轮滑转，且由随后的分析可知，其对车辆侧向性能也有一定的改善。

3.2 高低附着对接路面时直线加速

任一车轮遇到低附着路面时，该驱动轴即为低附着情形。取 μ左前= 0.3, μ右前= μ左后=μ右后=0.8，采用与 1）相同的初始条件和驾驶员输入，加速过程中电机输出转矩和纵向车速、前轴以及后轴各轮胎滑转率的仿真结果分别如图5a、5b以及5c所示：转矩平均分配时，左前轮滑转率同样很快超过70%，8 s时车速约为29.1 m/s；而转矩主动分配时，因前轴附着条件较后轴差，故前电机大约有25 N·m的转矩被转移至后电机，即前、后电机分别输出125、175 N·m，以充分利用后轴附着余量，在完全不牺牲驾驶员期望的同时将整体滑转率控制在5%以内。加速8 s时，车速约为32 m/s，比平均分配时提升9.9%。显然，对于对接路面，转矩主动分配策略对牵引力提升极为明显，且能很好地抑制车轮打滑。

图4 分离路面仿真结果Fig.4 Simulation results on split road surface

3.3 前、后轴处于均一低附着路面时转弯

由前面第 2节分析可知，车辆不发生过度滑转而处于附着稳定区时，具有较大的侧向附着力。考虑在低附着路面上车辆从一个车道变换至另一车道的工况，并取路面附着系数为0.3，初速度为 5 m/s，驾驶员给定转矩200 N·m。转弯过程中，前后电机输出转矩如图6a所示，各轮胎滑转率如图6b所示，前轮在2 s时刻开始按“周期为8 s，幅值为0.1 rad（约5.7º）的正弦曲线正半周”偏转，所对应的车身横摆角速度及质心侧偏角如图6c所示。转矩平均分配时，在2～6 s的转向过程中内侧车轮发生明显滑转，而质心侧偏角峰值已远大于 5°（一般认为非专业驾驶员可操控的侧偏角上限[15]为5°），横摆角速度也与期望值（由线性二自由度模型计算得到的参考值[28-29]）相差较远，此时车辆已经失稳；转矩主动分配时，在转向过程中，内外两侧车轮的滑转率均有所增加，但因前、后电机输出转矩均受到一定的限制，使得内侧车轮滑转率被控制在0.12～0.14之间，外侧车轮在0.02～0.06之间，质心侧偏角峰值不超过4°，处于安全上限5°以内，横摆角速度与期望值也比较接近，整个转向过程虽存在一定的转向不足，但基本能够实现转向需求，表明转矩主动分配策略对车辆在低附着路面上的侧向动力学性能有一定的改善作用。

图5 对接路面仿真结果Fig.5 Simulation results on joint road surface

图6 转弯工况仿真结果Fig.6 Simulation results under turning condition

4 控制器在回路测试

4.1 控制器软硬件设计

转矩分配控制器（Torque distribution controller，TDC）主要负责根据驾驶员输入和车辆实时状态，按照所制定的控制策略（式（39）、式（40））决策出前、后电机的目标输出转矩，并发送至前、后电机控制器，其硬件电路主要包括Freescale/MC9S12XEP100最小系统、电源模块、AD采样电路、CAN总线驱动电路等，TDC实物如图7所示。软件部分分为主程序和中断服务程序，主程序主要对各模块进行初始化，并在进入主循环后依次完成车辆输入的协议信息解析、前后电机目标转矩值的计算、更新发送报文内容并按照数据传输协议规定的周期完成前、后电机目标转矩的发送；中断服务程序主要负责从CAN总线上接收车辆实时状态信息，控制流程如图8所示。

图7 转矩分配控制器Fig.7 Torque distribution controller

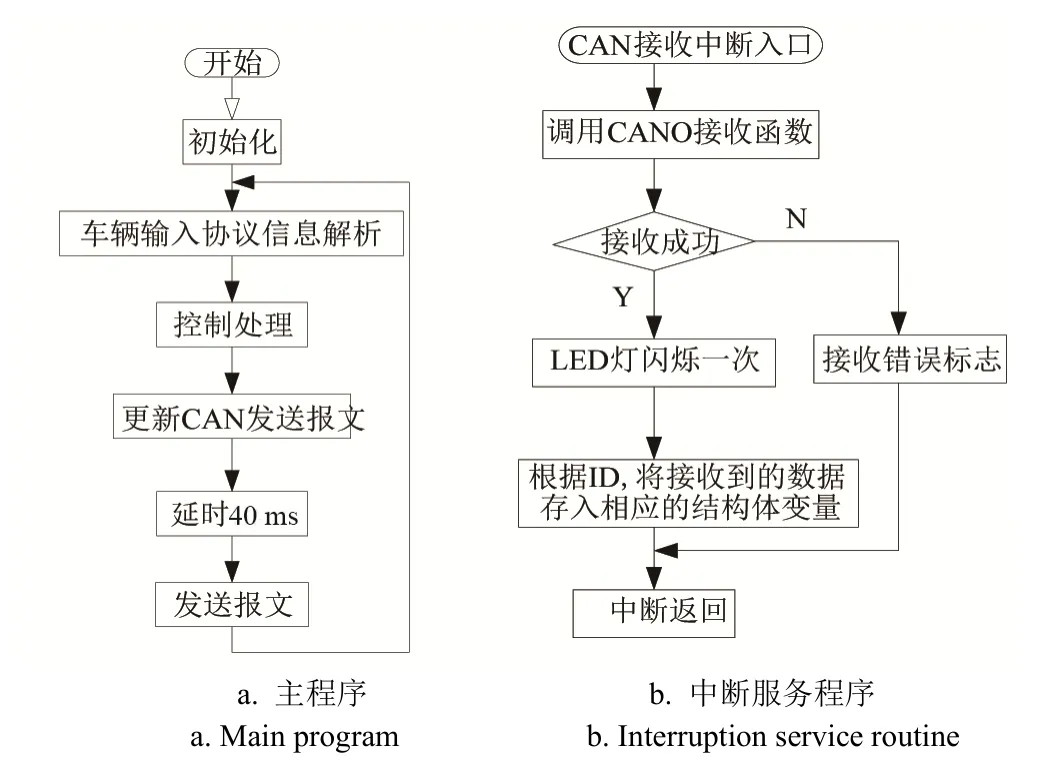
图8 主程序及中断服务程序控制流程图Fig.8 Flowcharts of main program and interruption service routine

4.2 硬件在环平台搭建

硬件在环测试系统（hardware-in-loop test system）以实时处理器运行仿真模型来模拟被控对象的运行状态，实现对真实控制器全面、系统的测试。为了测试TDC在各种工况下的实时性能，设计了基于 dSPACE的控制器在回路仿真测试平台[30]，如图9所示。

图9 硬件在环测试系统Fig.9 Hardware-in-loop test system

搭建测试平台时，针对图 3中的车辆动力学模型，利用 dSPACE/RTI实时接口库对其输入输出接口进行配置，经目标编译器编译成功后，下载至dSPACE/DS1007实时处理器以模拟被控车辆对象，并经专用CAN接口卡/DS4302与TDU相连，实现TDU与被控车辆之间的实时通信，二者之间的协议通信内容主要包括纵向及侧向车速、横摆角速度、车轮转速、纵向及侧向加速度、地面反力及前后电机目标输出转矩，见表3。此外，驾驶员给定的总驱动转矩和车轮偏转角则由TDU通过AD0、AD1两个通道分别采集到的加速踏板和方向盘电压值计算得到。上位机Control Desk可对车辆运行状态进行实时监控和数据记录，同时可作在线调参。

4.3 测试结果分析

下载至dSPACE/DS1007中的整车模型参数取值同表2，以模型仿真时的驾驶员给定作为期望值操纵加速踏板和方向盘，采用转矩主动分配控制策略时，针对分离路面、对接路面以及转弯3种工况的测试结果分别如图10、11及12所示。

表 3 TDC与dSPACE之间的通信内容Table 3 Communication messages between TDC and dSPACE

图11 对接路面测试结果Fig.11 Testing results of joint road surface

图12 转弯工况测试结果Fig.12 Testing results under turning condition

在分离路面时，图10a显示了前、后电机输出转矩的调节过程，由图 10b可知，左侧也即低附着一侧车轮滑转率被控制在0.1附近，与模型仿真结果（图4b）一致；在对接路面上，前轴附着系数较低，为充分利用后轴路面条件，前电机部分转矩被转移至后电机，见图11a，从而将前、后轴滑转率控制在0.05附近，如图11b、11c所示，这同样与模型仿真结果（图5b、图5c）一致；转弯工况中，前轮在6 s时按图12a偏转，内侧（左前、左后）车轮因轮荷较小而滑转率增长较快，在转弯开始不久（约6.5 s时刻）便已超过目标滑转率0.12，如图12e、12f所示，此时，TDC开始对电机输出转矩做出调整，由于地面附着系数较低，且用于转弯的侧向力已消耗了大部分地面附着极限，故前、后电机输出转矩被TDC调整到接近零输出的状态，见图12d，直到转向过程结束。由于转向过程短暂且纵向可用地面附着条件极其有限的缘故，TDC未能在较短的转向时间内通过调整电机输出转矩将内侧车轮的滑转率准确稳定在目标值 0.12（左前轮滑转率略高接近0.2，左后轮略低接近0，见图12e、图12f），同时，与软件仿真结果（图 6c）相比，车身侧偏角和横摆角速度也出现了一定程度的偏差，但基本处于可控范围内，如图12b、12c所示，对车辆在低附着路面上的转向能力仍有较大程度的改善。综合上述分析，所设计的控制器能够按照制定的控制策略合理分配前后电机输出转矩，在3种路况条件下均可避免车辆发生过度滑转。