一种基于新型损失函数的Listwise排序学习方法

龚 安，孙 辉，乔 杰

(1．中国石油大学(华东) 计算机与通信工程学院，山东 青岛 266580；2．中国石油大学(华东) 石油工程学院，山东 青岛 266580)

0 引 言

近年来，排序学习方法以其优异的性能成为信息检索与机器学习交叉领域中的“骄子”[1]。排序学习方法按照训练样本的不同分为点方式、对方式和列表方式[2-4]。研究表明，Listwise是排序学习中效果较好的一种算法，为了获得整个序列的排序情况，在实现过程中将整个文档序列看成一个训练样本，不仅结果展示自然，并且实现了对不同查询文档进行区分的功能[5-7]。在排序过程中，损失函数用来评价预测结果与真实结果之间拟合程度的高低，所以损失函数的构建尤为重要。

针对损失函数，研究人员在优化改进、降低时间复杂度等方面取得了比较大的进步。文献[8]提出了一种SHF-SDCG(smoothed hinge function-smoothing discounted cumulative gain)损失函数融合方法，将Pairwise方法损失函数与Pointwise方法的损失函数相融合，效果显著，但是时间复杂度高。文献[9]提出用位置近似函数来平滑文档位置损失函数，忽视了由单个文档位置变化造成的损失。文献[10]在降低训练过程时间复杂度的同时只考虑列表前端位置，缺乏对位置信息的利用。

基于此，文中提出了一种改进的Listwise排序学习算法，以整排列表作为输入，通过引入Pointwise损失函数及位置加权因子，对Listwise损失函数进行融合，并采用效率更高的Top-k训练方法。最后，在LETOR4.0数据集进行实验，对算法性能进行验证。

1 改进的Listwise排序学习算法

1.1 Listwise排序学习方法

Listwise将整个文档序列看作一个样本，通过优化信息检索和定义损失函数来得到排序函数。

Listwise采用概率模型计算列的损失函数，即通过概率模型把一列得分映射成概率分布，然后使用概率分布的度量作为损失函数[11-12]。度量分布通常有两种方法：组合概率和Top-k概率。当文档数较多时，组合概率会增大计算量，故通常选择Top-k概率来解决这个问题。

1.2 损失函数的融合

排序学习的过程就是不断优化损失函数的过程，在确定损失函数后，对其不断优化，直到找到损失函数最小时的参数，最后得到排序函数模型。

1.2.1 损失函数分类

(1)Pointwise损失函数。

(1)

其中，yj为训练集合中文档位置为j的对象的相关性标注分；f(xj)为学习排序函数对文档xj的相关性预测值。

Pointwise方法的训练样例是单个文档，它关注每个文档与查询的相关性大小，但是忽略了不同文档与查询相关性的大小关系，同时它也是人工神经网络中经常用于衡量训练样例的预测值与真实值之间误差的函数。

(2)Pairwise损失函数。

(2)

(3)

其中，oj=f(xj)，ojk=f(xj)-f(xk)。

Pairwise方法的训练样例是偏序文档对，它将对文档的排序转化为对不同文档与查询相关性大小关系的预测。

(3)Listwise交叉熵损失函数。

(4)

其中，Gk为Top-k前k个对象。

Listwise方法将文档序列作为整体考虑，认为用户关心的主要是位于文档序列前列的文档，从而忽略了每个文档与查询相关性的大小。

1.2.2 引入位置加权因子

排序的目的是将每个文档按照查询相关性进行排序，从而获取文档在整个序列的位置。由于衡量排序预测效果最明显的方法是和真实序列中的每篇文档所处的位置作比较，因此引入位置加权因子，即当文档排列出现错位时，就将该文档所在位置的倒数乘以位置损失的平方(位置损失就是预测得分与实际得分的差值)，就可以使相关文档(根据相关性得分)的排列更靠前，不相关文档更靠后，提高整体的排序质量。

训练集中的数据包含许多查询及查询项对应的文档，每个文档都有相关性得分，假设查询之间服从独立分布。例如，{q1,q2,…,qn}是查询集，qj表示第j个查询，Dj={dj,1,dj,2,…,dj,m}，其中Dj表示查询qj所对应的文档集合，yj={yj,1,yj,2,…,yj,m}，yj表示每个文档所对应的得分。特征向量xj由特征函数φ(·)得到，训练特征集可以表示为x={x1,x2,…,xn}，排序函数为f(x)，则查询每个qj所对应的文档集的位置加权因子为：

(5)

1.2.3 融合产生新型损失函数

综合上述Pointwise、Listwise方法的优缺点分析，引进位置加权因子，依据SHF-SDCG损失函数的融合框架，进行损失函数融合，得到新的损失函数：

L=Lpt×Tm+(1-Tm)×(Lls×Tm+(1-Tm)×Lp)

(6)

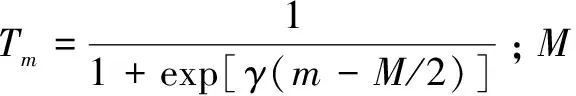
1.3 改进的Listwise排序学习算法

文中采用双层神经网络模型，借助误差反向传播算法以达到调节权值ω的目的，然后使用梯度下降优化损失函数L得到排序模型。其算法具体描述如下：

输入：训练集{(x(1),y(1)),(x(2),y(2)),…,(x(m),y(m))}

参数：设置迭代次数T，学习率η并初始化权重ω0。网络输入层单元数为nin，网络隐藏层单元数为nhidden

输出：改进的Listwise排序模型

1.创建nin个网络输入单元，nhidden个网络隐藏层单元，一个输出单元的网络，按照ω0初始化网络初始权重值。

2.fort=1 tot=T

3.fori=1 toi=m

4.输入查询q(i)的对应特征x(i)到神经网络，并且计算输出得分f(xi)，同时计算Lpt、Lls以及Lp

6.更新网络权重ωt+1=ωt-η×ωt

7.End for

8.End for

其中

f(x)=ω·x

(7)

对损失函数进行梯度计算：

(8)

(9)

Tm×(1-Tm)2

(10)

(11)

2 实 验

2.1 数据集

实验采用Letor4.0数据集中的TREC 2008，该数据集为46维数据，每一行表示一个样本文档，第一列是样本相关度，第二列是查询qid，其他列包含46维文档特征索引以及相应的特征值，例如：BM25、IF、语言模型等内容特征，PageRank等基于网页分析的特征。该数据集采用5折交叉验证策略，分为5组，每组有三个学习子集：训练集、验证集和测试集。规模较小的验证集被用来确定最佳迭代次数以及网络权重。

2.2 评价标准

采用NDCG(normalized discounted cumulative gain)评价指标，它是用来衡量排序质量的指标，当所有相关文档排在不相关文档的前面时，NDCG值最大[13-15]。其定义如下：

(12)

其中，Zn为归一化因子；r(j)为第j个位置文档的标签，j为位置。

2.3 实验设计

文中算法实验设定隐藏层的权值为较小的随机值[-0.2，0.2]，输入层的权值设定为0或者较小的随机值[-0.01，0.01]，初始学习率为0.003，在每次学习中，如果上次迭代的平均误差小于所有样例的平均误差，则将学习率降为一半。最后将文中算法与Pointwise方法中的Regression算法、Pairwise方法中的RankSVM算法和基于SHF-SDCG改进的RankNet算法及Listwise方法中的ListNet算法进行实验对比。

2.4 实验结果对比与分析

采用NDCG@K，实验结果对比如表1所示。为了使结果对比更加直观，将表1数据用直方图表示出来，如图1所示。

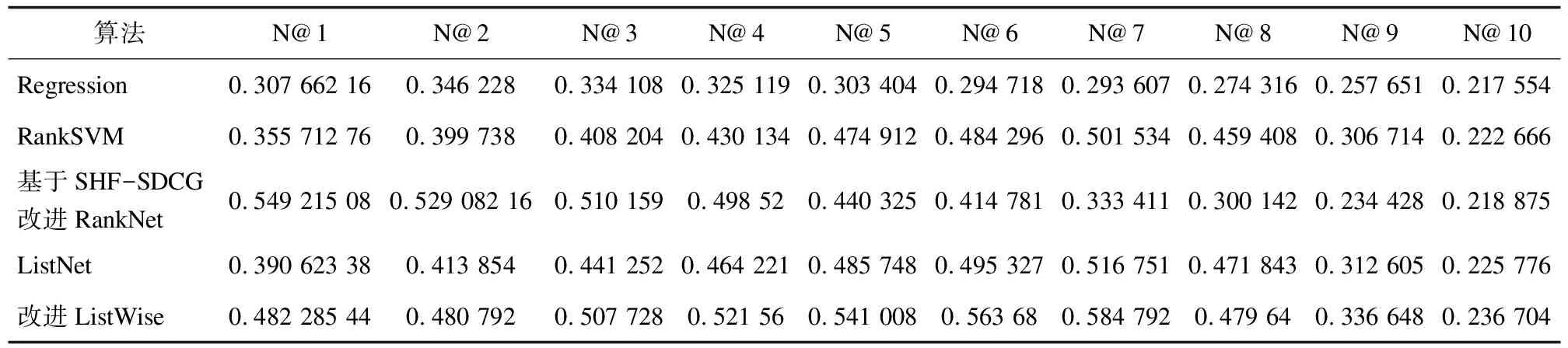
表1 NDCG@K值的比较

图1 NDCG@K值的比较

从图中可以看出，Listwise算法要优于其他算法，主要原因是Listwise方法比Pointwise方法、Pairwise方法更加直接自然，可以区分不同查询中的文档。当k=1,2,3时，基于SHF-SDCG改进的RankNet要优于其他算法，主要原因是在Pairwise方法中增加了对单个文档相关性的考虑，不会出现因为文档对内两个文档的相关性预测错误而导致连锁反应影响最终排序性能的现象，并且当k比较小时，改进Pairwise方法无限接近于Listwise方法，并且在排序性能上要优于Listwise方法。而当k=5,6,…,10时，改进Listwise方法的NCDG@k值比较大且稳定，主要原因是当k较大时，改进Listwise方法较其他方法不仅考虑了相关文档位置，而且引入了Pointwise损失函数，更加全面地考虑了排序的各个方面。

综上所述，改进Listwise方法得到的排序列表中的相关文档排在列表前面位置的情况要优于Listwise、Pointwise、Pairwise等方法。

3 结束语

通过对排序效果最自然、效果较好的Listwise方法进行研究，在现有SHF-SDCG损失函数融合框架的基础上，引入位置加权因子以及Pointwise损失函数，分别采用梯度下降算法和多层神经网络算法训练网络权重值，对Listwise算法进行了综合改进与优化，解决了原算法存在的时间复杂度高、排序位置信息利用度低等问题。为了验证改进之后Listwise算法的优越性，选用Letor4.0数据集中的TREC 2008进行实验，NDCG值的对比证实了改进算法在排序过程中取得了较好的实验效果。