蜂窝网络下行链路中基于干扰图的干扰对齐算法

杨 真 刘祖军 田红心

(西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西西安 710071)

1 引言

干扰会严重降低蜂窝网络的容量，尤其是位于小区边缘的用户受到相邻基站的干扰远强于小区中心的用户。干扰对齐技术[1]作为一种有效提高系统容量的手段，被证明可应用于蜂窝网络通信。

多小区多用户下行链路中，由于多用户共享信道资源，因此同时存在区间干扰(ICI)和用户间干扰(IUI)。目前针对多小区多用户下行链路的干扰对齐算法主要是分布式的迭代干扰对齐算法和基于求封闭解的干扰对齐算法。分布式的迭代干扰对齐算法[2- 4]将最小化干扰泄露或最大化信干噪比的思想应用到蜂窝网络，只需要了解本地信道状态信息(CSI)。但当小区数过大时，目标函数很难收敛，并且时间复杂度随着小区数增加而指数增长。

与之相比，基于求封闭解的干扰对齐算法[5- 6]无需迭代，可以直接求解满足干扰对齐条件[7]的波束赋形矩阵。然而，小区数增加时，信道中的用户对数目也线性增加，研究表明K用户干扰信道的总约束条件依O(K2)增长[8]。干扰对齐需要足够的空间维度，因此当小区数及用户数增加时，每个节点的收发天线数线性增长。为了尽量减少所需天线数，文献[9]将干扰对齐到多维子空间(代替一维)解决两小区下行干扰问题。文献[10]针对两小区两用户提出一种干扰对齐方案，设计接收波束赋形矩阵将ICI对齐到子空间，再用发送波束赋形矩阵对IUI和ICI同时迫零。在文献[10]的基础上，文献[11]提出了一种将邻区干扰进行分组的方法，解决了三小区两用户下行链路的干扰对齐问题。然而，在大型蜂窝网络中，由于约束条件大量增加，这些算法不能实现完全干扰对齐。

如何将上述两小区或三小区的干扰对齐算法应用到庞大的蜂窝网络中？针对这一问题，分簇干扰对齐[12-13]的思想被引入到蜂窝网络。此方法根据已知收发天线数判断出可以分为一簇的小区数，并在每个簇内独立的使用干扰对齐技术。文献[19]提出针对单用户蜂窝网络分簇模型的干扰对齐算法，降低了算法复杂度。文献[14]提出了一种单用户蜂窝网上行链路的干扰对齐算法，采用图论模型表征蜂窝网络的干扰分布(定义为干扰图)，并基于干扰图选定用于干扰对齐的簇，平移簇可以扩展到整个蜂窝网络，从而可以实现整个网络的干扰对齐。文献[14]适用于等效为干扰信道的单用户上行链路，只需要考虑ICI。

多用户蜂窝网络下行链路需要同时考虑ICI和IUI对用户的影响。协作多点传输(CoMP)是消除ICI、提高小区边缘用户吞吐量的关键技术[18]。但协作区域内多用户间干扰会影响系统容量，并且相对于CoMP,利用定向干扰消除，只需要本地单方向信息交换，减少了回程链路。因此本文结合定向干扰消除技术，设计了一种蜂窝网络下行两用户场景下的干扰对齐算法。首先用无向干扰图表示蜂窝网络，利用基站协作按照“从左到右”“从上到下”的顺序消除部分定向干扰，得到有向干扰图。在此基础上，根据小区分布选择五个小区组成簇，在簇内处理ICI和IUI。根据收发天线数分为两种情况进行了讨论：当收发天线数相等时，信道矩阵是可逆的，直接求干扰对齐波束赋形矩阵封闭解；当收发天线数不相等时，先通过设计接收波束赋形矩阵将ICI分组方法，再设计发送波束赋形矩阵与IUI及ICI正交。分别分析两种情况下满足干扰对齐条件的最少收发天线数。最后计算平均每小区可达自由度，并仿真簇数增加到5时蜂窝网络的速率和性能。

2 蜂窝模型

图1 蜂窝模型

图2 复平面的艾森斯坦整数

首先，利用基站间本地回程连接实现发送端协作，蜂窝网络的基站按照“从右到左”“从下到上”的顺序连续编码。例如，考虑两个相邻小区的基站1和2，当基站1排列在基站2的右方或下方时，可以通过回程链路将编码信息传递给基站2，这样消除掉部分定向干扰[14]。为了降低干扰对齐实现的复杂度，将坐标Λ0=2·Z(w)的基站关掉，剩余小区定义为工作小区。用干扰图G(VV0,εε0)表示完成干扰消除及关闭部分基站后的蜂窝网络，如图3所示。其中，基站关闭的小区及其相邻连线(图中灰色部分)记为V0和ε0，工作小区及其相邻连线记为VV0和εε0。

图3 下行干扰图G(VV0,εε0)

自由度是在高信噪比(SNR)情况下，无线通信MIMO系统性能的重要指标，工作小区内自由度定义为

(1)

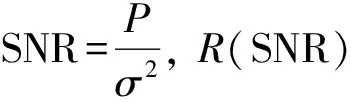
所有工作小区的自由度是相等的，因此整个蜂窝网络(包括工作小区和关闭小区)平均每小区可达DoF定义为[14]

(2)

其中，|V0|表示关闭小区数量，|V|表示全部小区(包括关闭小区)数量。

自由度的计算分为两步：(1)从物理层实现簇内干扰对齐，计算出工作小区的自由度dν；(2)从整个网络层角度计算蜂窝网络平均每小区的自由度dG。

3 基于干扰图的干扰对齐算法

基于干扰图的干扰对齐算法分为三个步骤。首先，基于干扰图合理划分簇，然后使用干扰对齐技术设计簇内小区发送端及接收端的波束赋形矩阵。最后利用簇的平移实现蜂窝网络内全部工作小区的干扰对齐。

3.1 设计同构簇

设计簇时要满足以下几点，首先簇内节点和有向连线都完全相同，我们将其定义为同构簇；然后同构簇经过平移可以得到整个干扰图G(VV0,εε0)；同时簇内小区数尽量少，以使干扰对齐更易实现。因此我们选择如图4所示包含5个小区的同构簇，簇的中心节点坐标为z=Λ0+w(用黑色圆标记)，记为S(z)。

图4 同构簇S(z)

在单用户的蜂窝网络中，只需要考虑消除ICI即可。然而，当每小区增加一个用户后，如图5所示，需要同时处理ICI和IUI。图5中箭头表示区间干扰方向。

图5 同构簇的物理层示意图

每个簇内包含5个小区，每个小区内有两个用户，发送及接收天线数目分别为Nt,Nr。假设接收天线数Nr小于发送天线数Nt，则每个用户数据流数ds≤min(Nt,Nr)=Nr。小区i内的用户k表示为用户[k,i]，用户[k,i]的接收信号表示为

(3)

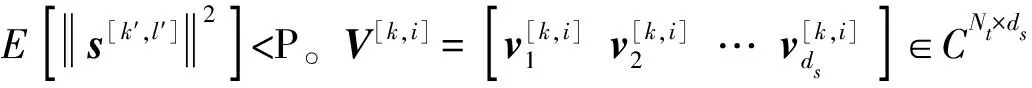
(4)

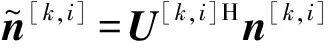
(5)

为了能得到有用信号，ICI和IUI都要对齐到与U[k,i]正交的子空间，因此得到如下干扰对齐可行性条件：

(6)

(7)

(8)

下面分别在对称及不对称信道两种情况下设计波束赋形矩阵，并对各自最少收发天线数进行分析。

3.2 对称信道的波束赋形矩阵设计

假设发送与接收天线数相等，此时波束赋形矩阵设计分为两步。

(1)接收波束赋形矩阵设计

接收波束赋形矩阵设计同样可以分为两步。

步骤1各自设计如图5中簇内小区3、4、5内用户的接收波束赋形矩阵，将来自相邻小区的4个ICI对齐到两个矢量空间。

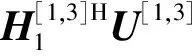
(9)

其中，D1,D2∈CNt×ds分别表示由基站1和2到小区3中两个用户的有效ICI张成的干扰空间，即为与经过接收机处理矩阵相乘之后，由基站1和2到小区3中用户ICI空间的交集。

(10)

其中，D3,D4∈CNt×ds分别表示由基站1和基站3到小区4中两个用户的有效ICI张成的干扰空间。

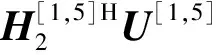
(11)

其中，D5,D6∈CNt×ds分别表示由基站2和基站3到小区5中两个用户的有效ICI张成的干扰空间。

步骤2对式(9)～(11)求解，得到接收波束赋形矩阵。

span(A)表示由A的列向量张成子空间。当Nt=Nr时，存在特征向量，可以得到满足上述条件的封闭解。由式(9)可以得到：

⟹span(U[1,3])=span(E3U[1,3])

U[1,3]=e3

(12)

同样可以得到，对于小区4内的用户有：

U[1,4]=e4

(13)

对于小区5内的用户有：

U[1,5]=e5

(14)

其中，e4,e5分别为矩阵E4,E5的特征向量。

(2)发送波束赋形矩阵设计

通过接收波束赋形矩阵的设计，已经将来自相邻基站的四个ICI分别对齐到两个子空间，因此对于每个用户可以消除掉两个ICI。

(15)

(16)

(17)

引理1假设存在3个小区，每小区2个用户，每个用户期望数据流个数为ds。由式(18)得到发送波束赋形矩阵，式(12)～(14)得到接收波束赋形矩阵。则发送天线数Nt与接收天线数Nr最少为4ds

(18)

证明：已知可行性条件式(8)中信道矩阵满秩，因此当rank(U[k,i])=ds且rank(V[k,i])=ds时，(8)成立。用户[k,i]的发送波束赋形矩阵V[k,i]均为计算某一矩阵L[k,i]的零空间，如式(18)。当且仅当L[k,i]有一个维数至少为ds的零空间时，V[k,i]才存在。L[k,i]的维数是3ds×Nt，因此发送天线数Nt最少为4ds，接收天线数等于发送天线数，同样最少为4ds。

证毕。

3.3 非对称信道的波束赋形矩阵设计

假设发送与接收天线数不相等，可采用分组的方法设计接收波束赋形矩阵，分为以下两步。

(1)用户分组及接收波束赋形矩阵设计

如图5所示，每个小区受到两个相邻小区的ICI，例如小区3内用户受到基站1、2的干扰。依此将5个小区分为三组，小区1、3、4为一组，小区1、2、3为一组，小区2、3、5为一组。每组内再进行分组干扰对齐，思想是将来自其中一个小区的ICI对齐到子空间，达到节省天线数的目的。举例来说，通过设计U[1,4]和U[2,4]将基站1到小区4中用户[1,4]，[2,4]的干扰信道对齐到相同的子空间G1。同理，将基站2到小区3中用户[1,3]，[2,3]的干扰信道对齐到相同的子空间G2，基站3到小区5中用户[1,5]，[2,5]的干扰信道对齐到相同的子空间G3：

(19)

(20)

(21)

通过求解(22)～(24)可得到满足条件(19)～(21)的交集子空间：

(22)

(23)

(24)

(2)发送波束赋形矩阵设计

因为ICI已经对齐，基站1可以将发送到小区4的两个干扰看作一个，小区1内发送波束赋形矩阵V[k,1]设计如式(25)。同样，小区2、3发送波束赋形矩阵设计为式(26)～(27)。

(25)

(26)

(27)

引理2假设存在L个小区，每小区K个用户，每个用户期望数据流个数为ds。由式(28)、(29)分别得到发送和接收波束赋形矩阵，则发送天线数Nt≥[K(L-1)+1]×ds，接收天线数Nr≥[(K-1)(L-1)+1]×ds。

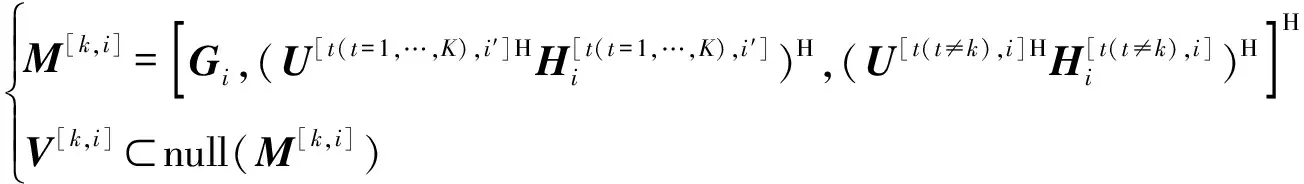
(28)

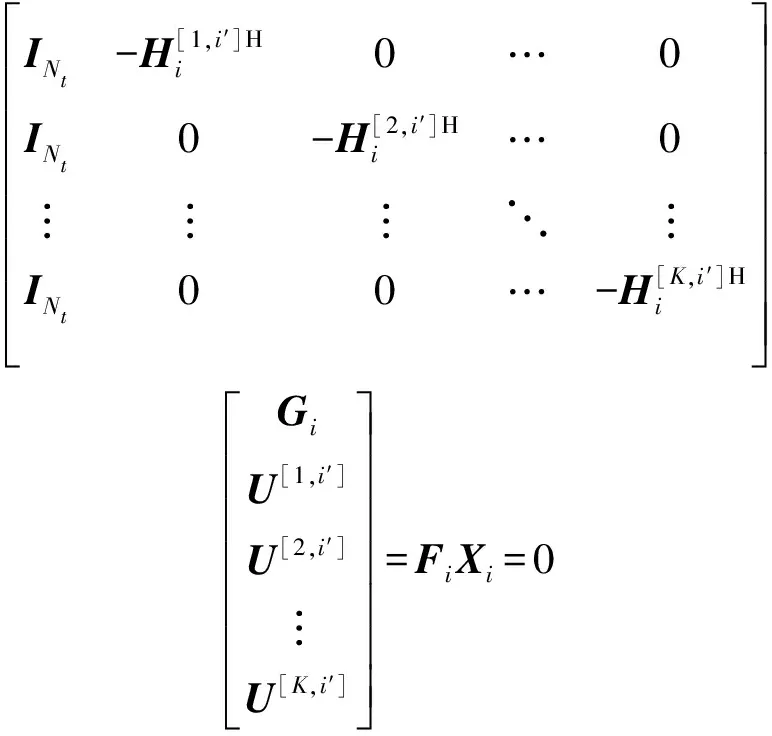
(29)

证明：已知可行性条件式(8)中信道矩阵满秩，因此当rank(U[k,i])=ds且rank(V[k,i])=ds时，(8)成立。用户[k,i]的发送波束赋形矩阵V[k,i]均为计算某一矩阵M[k,i]的零空间，如式(28)。当且仅当M[k,i]有一个维数至少为ds的零空间时，V[k,i]才存在。M[k,i]的维数是[K(L-1)ds]×Nt，因此发送天线数Nt最少为[K(L-1)+1]×ds。

证毕。

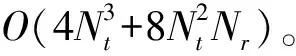
3.4 簇的平移

我们已经设计了簇S(3)内小区1、2、3内基站的发送波束赋形矩阵及小区3、4、5内用户的接收波束赋形矩阵。然后将簇S(3)向右平移到簇S(3′),如图6所示。此时可以在簇S(3′)中计算基站4的发送波束赋形矩阵。此时两个簇间的干扰可以看作小区4与小区3′的ICI，因此消除ICI的同时解决了相邻簇间的干扰。如图3所示，斜框1内是设计的簇，上下左右平移依次可以得到斜框3、5、2、4内的同构簇，继续四周平移最终得到整个干扰图。而在蜂窝网络边缘位置的小区只处理用户间干扰，本文中不再详细讨论。

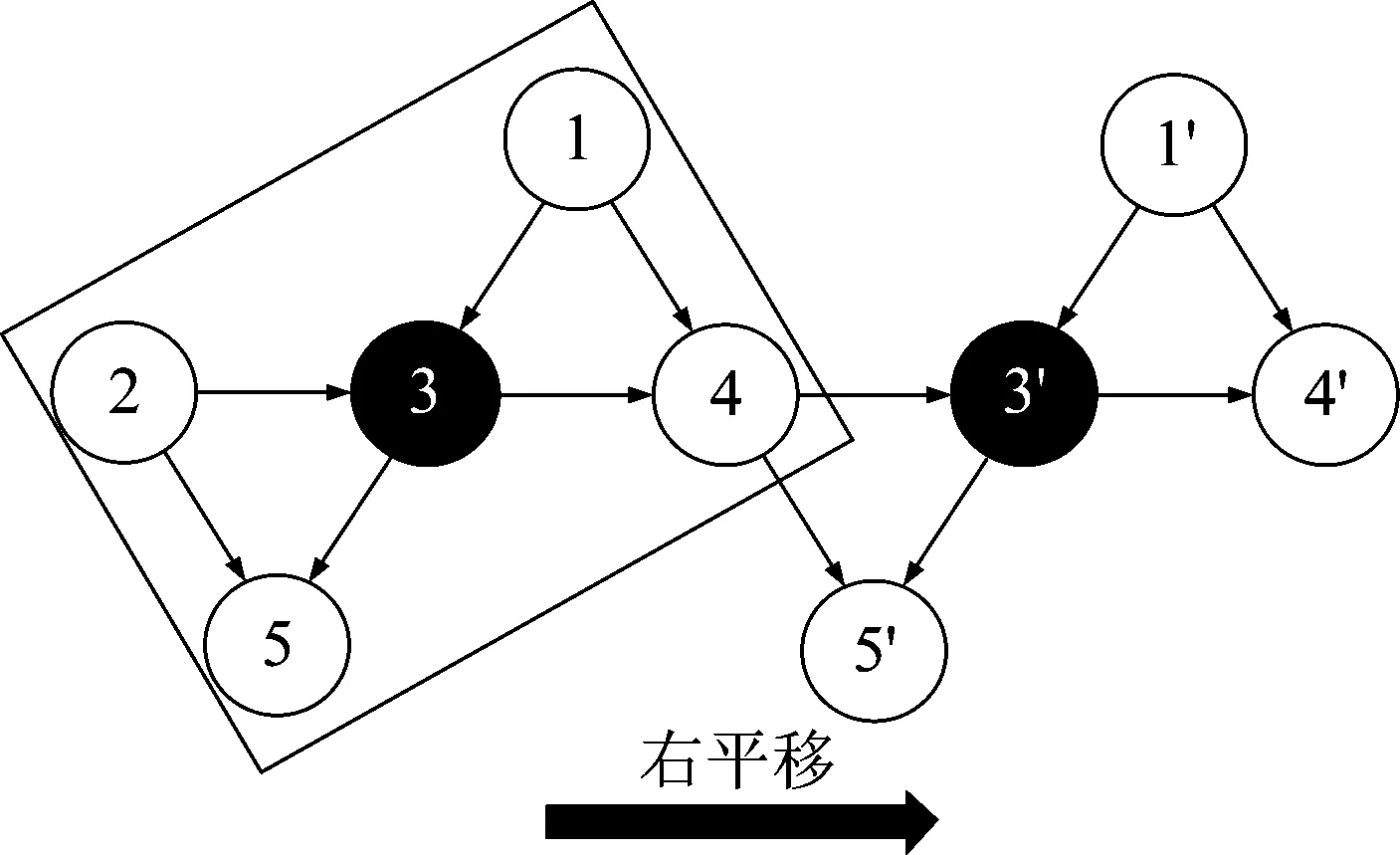
图6 簇的右平移示意图

4 仿真结果

本节对提出的基于干扰图的干扰对齐算法进行仿真。忽略蜂窝网络的边缘小区，图6为簇数1增加到簇数2的情况，当簇数为1时，计算小区1、2和3内用户的速率和，簇数增加到2时，计算小区1、2、3、4和1′、3′共6个小区内用户的速率和。以此类推，分别向四周平移后，仿真簇数增加到5时的速率和性能。

假设所有基站的发送功率固定为P，每个用户所有天线的噪声方差都为σ2。图7和图8分别为系统配置(Nt,Nr,K,ds)=(4,4,2,1)和(Nt,Nr,K,ds)=(5,3,2,1)时的仿真结果。从图中可以看出，高信噪比下速率和线性增加，斜率即为自由度。两图中同构簇数从1到5的曲线斜率分别为6、12、18、24、30。相同场景下，文献[15]提出的基于用户协作的干扰对齐算法接收天线数Nr=5时，DoF可达到6。传统的迫零波束赋形算法需要发送天线数Nt=6[6]，可见本文使用的两种算法均减少了收发天线数。

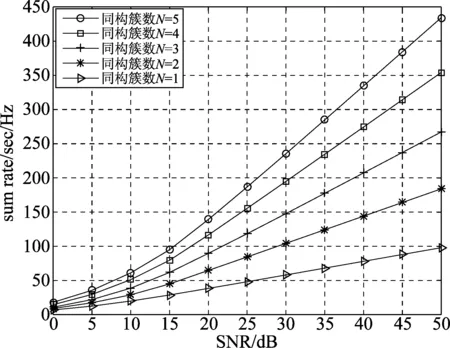
图7 对称信道情况下可达速率和(Nt=Nr=4)

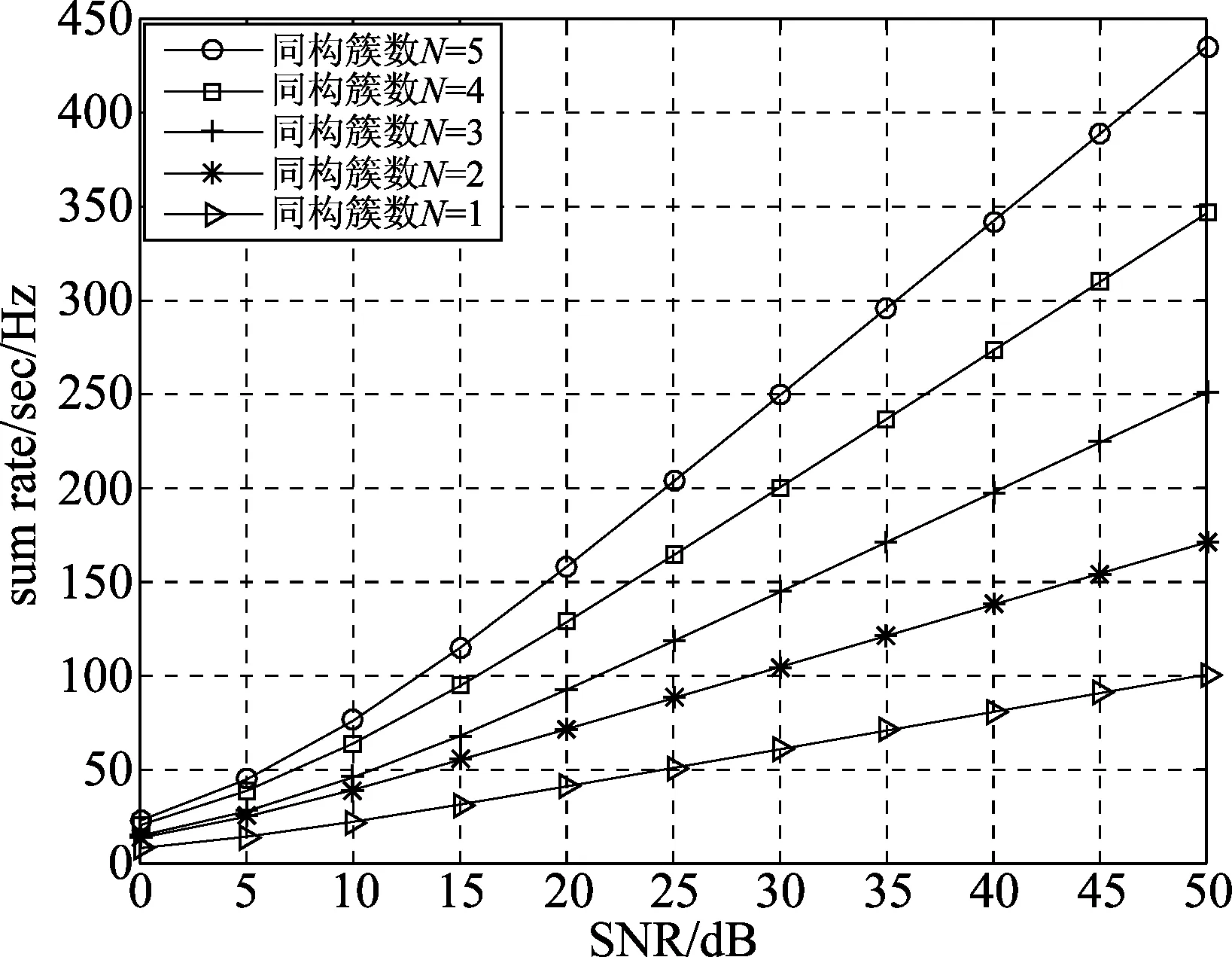
图8 不对称信道情况下可达速率和(Nt=5,Nr=3)

图9及图10分别为系统配置(Nt,Nr,K,ds)=(4,4,2,1)和(Nt,Nr,K,ds)=(5,3,2,1)情况下工作小区平均每小区的自由度。可以发现，随着同构簇数量增加，曲线逐渐重合。因此证明随着簇的平移，算法在消除簇内的ICI和IUI的同时，也消除了簇间干扰，使工作小区达到相同的最优自由度。

图9 平均每小区可达速率和(Nt=Nr=4)

图10 平均每小区可达速率和(Nt=5,Nr=3)

5 结论

为了消除蜂窝网络多用户下行链路的ICI及IUI，本文提出了一种基于干扰图的干扰对齐算法。将蜂窝网络分簇后，分别用求封闭解和分组的干扰对齐算法联合设计了波束赋形矩阵。该算法与传统多小区下行链路的干扰对齐算法相比，小区数不受限制，并且减少了基站天线数和复杂度。仿真结果证明了所提算法不仅可以消除一个簇内的ICI和IUI，并且随着蜂窝网络扩展速率和性能不受影响，提高了蜂窝网络的容量增益。

[1] Cadambe V R, Jafar S A. Interference alignment and degrees of freedom of the K-user interference channel[J]. IEEE Transactions on Information Theory, 2008, 54(8): 3425-3441.

[2] Schreck J, Wunder G. Distributed interference alignment in cellular systems: analysis and algorithms[C]∥Preceedings of European Wireless 2011, Vienna, 2011: 109-116.

[3] Zhuang B, Berry R A, Honig M L. Interference alignment in MIMO cellular networks[C]∥Preceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Prague, 2011: 3356-3359.

[4] Schmidt D A, Shi C, Berry R A， et al. Minimum mean squared error interference alignment[C]∥Signals, Systems and Computers, 2009 Conference Record of the Forty-Third Asilomar Conference on. IEEE, 2009: 1106-1110.

[5] Suh C, Ho M, Tse D N C. Downlink interference alignment[J]. IEEE Transactions on Communications, 2011, 59(9): 2616-2626.

[6] Tresch R, Guillaud M, Riegler E.On the achievability of interference alignment in the K-user constant MIMO interference channel[C]∥Statistical Signal Processing, 2009. SSP'09. IEEE/SP 15th Workshop on. IEEE, 2009: 277-280.

[7] Bresler G, Cartwright D, Tse D. Feasibility of Interference Alignment for the MIMO Interference Channel[J]. IEEE Transactions on Information Theory, 2013, 60(9):5573-5586.

[8] Jafar S A.Interference Alignment-A New Look at Signal Dimensions in a Communication Network[J]. Foundations & Trends® in Communications & Information Theory, 2010, 1(1):1-136.

[9] Suh C, Tse D. Interference alignment for cellular networks[C]∥Communication, Control, and Computing, 2008 46th Annual Allerton Conference on. IEEE, 2008: 1037-1044.

[10] Shin W, Lee N, Lim J B, et al. On the Design of Interference Alignment Scheme for Two-Cell MIMO Interfering Broadcast Channels[J]. Wireless Communications IEEE Transactions on, 2011, 10(2):437- 442.

[11] Tang J, Lambotharan S. Interference alignment techniques for MIMO multi-cell interfering broadcast channels[J]. IEEE Transactions on Communications, 2013, 61(1): 164-175.

[12] Tresch R, Guillaud M,Riegler E. A clustered alignment-based interference management approach for large OFDMA cellular networks[C]∥Joint NEWCOM++/COST2100 Workshop on Radio Resource Allocation for LTE. 2009.

[13] Tresch R, Guillaud M. Performance of interference alignment in clustered wireless ad hoc networks[C]∥IEEE International Symposium on Information Theory. IEEE, 2010:1703-1707.

[14] Ntranos V, Maddah-Ali M A, Caire G. Cellular interference alignment: Omni-directional antennas and asymmetric configurations[J]. IEEE Transactions on Information Theory, 2015, 61(12): 6663- 6679.

[15] Shin W,Lee N,Lim J B.User cooperation-assisted multi-cell MIMO networks[C]∥IEEE Mtt-S International Microwave Workshop Series on Intelligent Radio for Future Personal Terminals. IEEE, 2011:1- 6.

[16] Holmes M P, Gray A G, Isbell C L. Fast SVD for large-scale matrices[C]∥In Workshop on Efficient Machine Learning at NIPS, Whistler,Canada,2007.

[17] Golub G H,Loan C F V.Matrix Computations[M].The Johns Hopkins University Press,1996.

[18] 3GPP TR 36.814 vO.4.1,2009.02．Further Advancements for E-UTRA: Physical Layer Aspects(Release 9)[S]．3GPPTSG RAN，2009.02．

[19] 代龙震, 崔维嘉, 王大鸣. 蜂窝系统自适应K近邻干扰对齐算法[J]. 信号处理, 2016, 32(3):313-320.

Dai Longzhen, Cui Weijia, Wang Daming. An Adaptive K-nearest-neighbor Interference Alignment Algorithm in Cellular System[J].Journal of Signal Processing, 2016, 32(3):313-320. (in Chinese)