利用功率谱最大最小平均比的频谱感知算法

毛翊君 赵知劲 吕 曦

(杭州电子科技大学通信工程学院，浙江杭州 310018)

1 引言

认知无线电(Cognitive Radio, CR)[1]是一种高效频谱管理技术，频谱感知[2]是其关键技术之一。匹配滤波法、能量法[3]、循环平稳特征法和基于随机矩阵理论(Random Matrix Theory, RMT)的频谱感知算法[4 -5]等是常用窄带频谱感知算法。但这些算法各有千秋，前两种算法需已知主用户先验信息或噪声信息，后两种算法复杂度高，门限难以准确确定。近年来，基于功率谱的频谱感知算法[6-11]得到了广泛关注，它不需要特征值分解，计算复杂度低，且能准确得到算法判决门限。文献[7]利用功率谱最大最小值的比作为检测统计量，最小值直接取零频处的功率谱值，由于噪声影响，最小值的随机性降低了算法性能；对此，文献[8-10]采用功率谱分段对消的思想构造检测统计量，文献[11]分析了文献[10]算法检测统计量的随机变量之间存在相关性时的检测性能，指出文献[10]算法存在的不足之处，文献[11]利用功率谱中间一段的平均值代替最小值，提出了基于功率谱的平均比值算法(Power Spectral Ratio Averaging，PSRA)，PSRA算法性能优于文献[7-10] 算法。但实际接收系统中得到的基带信号往往存在载波频偏[12-13]，频偏将影响上述算法性能，针对此问题，本文提出一种利用功率谱最大最小平均比的算法(Power Spectral Maximum Minimum Averaging Ratio，PSMMAR)，将功率谱的最大值的平均值与最小值的平均值之比作为检测统计量，减小频偏和噪声不确定性对算法性能的影响。

2 PSMMAR算法

2.1 检测原理

CR中，次用户(Secondary User, SU)感知主用户(Primary User, PU)存在与否问题可表示成如下二元假设检验：

(1)

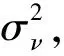
由于x(n)和ν(n)相互独立，则式(1)的二元假设检验模型可用功率谱表示如下：

(2)

其中，Py(w)、Px(w)和Pν(w)分别表示y(n)、x(n)和ν(n)的功率谱。分别对接收信号y(n)、有用信号x(n)和噪声ν(n)进行傅里叶变换，可得：

(3a)

(3b)

(3c)

y=[y(0),y(1),...,y(N-1)]T,x=[x(0),x(1),...,x(N-1)]T和ν=[ν(0),ν(1),…,ν(N-1)]T分别表示y(n)、x(n)和ν(n)的N个采样样本的向量形式，w=[1,e-jw,…,e-j(N-1)w]H,(·)T,(·)H表示向量的转置和共轭转置。通过周期图法可得功率谱估计为：

(4a)

(4b)

(4c)

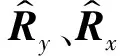
(5)

则有Q(w)|max=λ1，Q(w)|min=λN。又因为wHw=N，则可得：

λN≤Py(w)≤λ1

(6)

在H0假设下，λ1=λ2=…=λN，所以Py(w)|max=Py(w)|min；在H1假设下，λ1≥λ2≥…≥λN，则Py(w)|max=λ1>Py(w)|min=λN。根据功率谱在H0和H1假设下的差异，可得频谱感知的判决统计量T为：

(7)

则二元假设检验可表示为：

(8)

2.2 检测方法与检测门限

实际应用中，为了降低噪声对功率谱估计的影响，应对功率谱进行平滑处理。将接收信号y(n)的N个样本分成连续的L帧，每帧长度为M点，即N=L×M，记第i帧信号为：

yi(n)(i=0,1,…,L-1,n=0,1,…,M-1)

(9)

则平滑处理后的信号y(n)的离散功率谱估计为：

(10)

由此可知，当存在载波频偏时，r(n)的功率谱的最大值偏离了零频率。因此由Py(0)作为Py(w)最大值构成的检测统计量进行判决，将降低检测性能。又由于载波频偏未知和噪声影响，信号功率谱的最大值和最小值很难根据单个频点来准确估计。因此，利用接收信号零频率附近一段功率谱的平均值来估计功率谱的最大值，可以有效降低载波频偏对频谱感知性能的影响。同时，利用功率谱中段附近一段的平均值来估计功率谱的最小值，降低噪声对频谱感知性能的影响。因此本文利用式(11)和(12)分别估计功率谱最大值和最小值：

(11)

(12)

其中，K0表示估计功率谱最大值时所选取的功率谱长度；K1表示估计功率谱最小值时所选取的长度，K2表示功率谱的中点。频谱感知的判决统计量T修改为：

(13)

(14)

下面推导门限γ的计算。将Yi(k)表示成如式(15)所示形式：

(15)

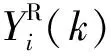
(16)

(17)

(18)

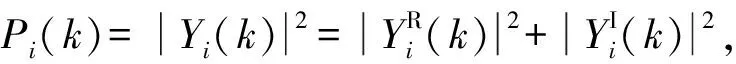
(19)

(20)

(21)

(22)

由于不同帧数据在相同频点上的Pi(k)相互独立，根据中心极限定理可得，当L足够大时，由式(10)可得，Py(k)近似服从如下所示高斯分布：

(23)

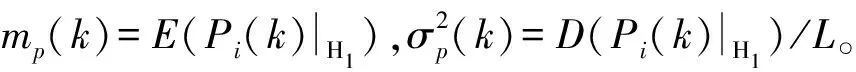
(24)

其中，erf(·)为误差函数。给定虚警概率Pf，则可得检测门限为:

(25)

其中，c表示常数[erf-1(2Pf-1)]2。从式(25)中可以看出，检测门限γ与噪声ν(n)的方差无关，因此理论上本文算法对噪声不确定性是鲁棒的。

2.3 算法流程

综上可得本文提出的利用功率谱最大最小平均比的频谱感知算法(PSMMAR)如下：

(1)根据式(25)计算门限值γ。

(2)利用式(9)和式(10)估计接收信号y(n)的功率谱密度Py(k)。

(4)根据式(13)计算检测统计量T。

(5)将T与γ比较，若T大于γ，则判定为H1成立；否则，判定为H0。

2.4 算法复杂度分析

本节分析PSMMAR算法、PSC算法和PSRA算法的复杂度并进行比较。

三种算法计算功率谱密度方法相同，区别在于检测统计量计算，而后者计算复杂度远小于前者，所以算法复杂度由前者决定。对接收信号y(n)的连续L帧、每帧长度为M点信号yi(n)进行M点离散傅里叶变换的复杂度为O(Mlog2M)，因此，三种算法的复杂度都为O(Nlog2M)。

3 算法仿真与性能分析

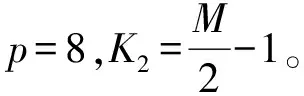
表1 判决门限值和虚警概率仿真值

由表1可知，由判决门限γ1得到的虚警概率与理论虚警概率一致，由判决门限γ2得到的虚警概率远高于理论虚警概率，所以γ1是正确的门限。下文中，每条曲线均是2000次的Monte Carlo模拟仿真结果的平均。

(2)K1对三种算法性能的影响。Pf=0.01，码元数为500，帧长M=48，Δf分别为0.04、0.05和0.06，K0=2，K1为4、6和8时，本文算法、PSRA算法和PSC算法在AWGN信道中的算法性能曲线分别如图1(a)、(b)和(c)所示。由图可见：1)随着Δf的增大，K1在一定范围内取值越大，算法性能越好；当K1值增大到一定值时，算法性能曲线趋于平稳。这是因为在K0确定后，K1越大，参与功率谱最小值平滑的样本就增加，从而功率谱最小值估计更加准确；当样本足够多时，功率谱最小值平滑结果基本不变，因此算法性能曲线就不再受K1值影响。2)在不同载波频偏系数下，本文算法性能受频偏的影响较小，其他两种算法性能受频偏的影响较大，即本文算法对频偏鲁棒性强。

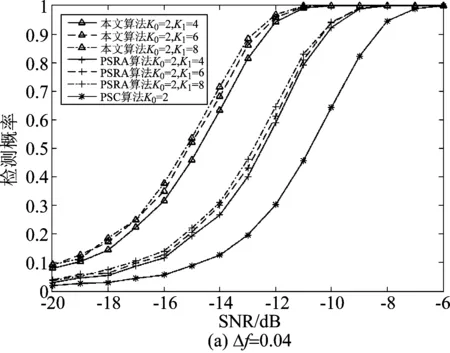
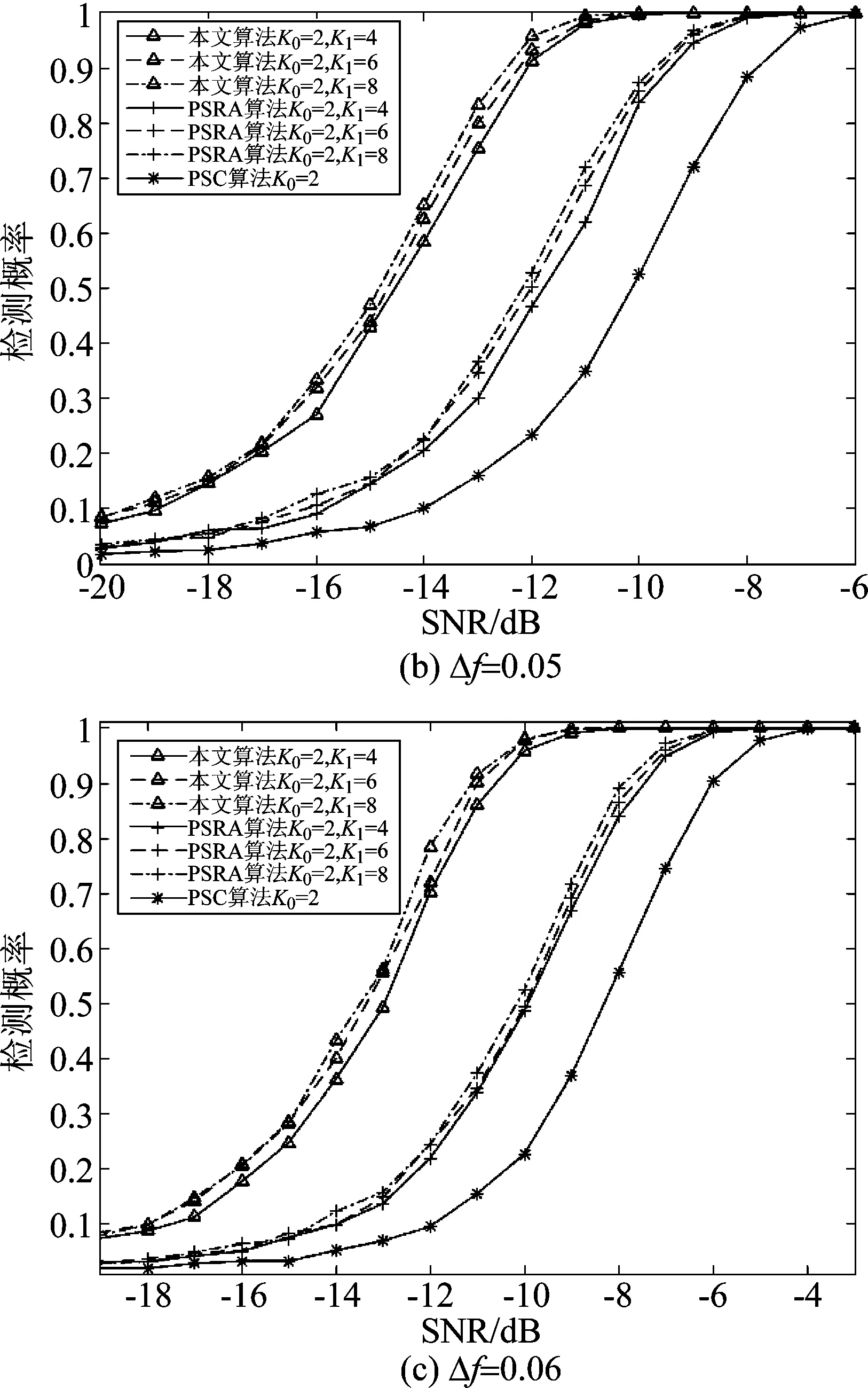
图1 Δf取不同值时，不同K1下的三种算法性能曲线

(3)K0对本文算法性能的影响。Pf=0.01，码元数为500，帧长M=16，载波频偏系数Δf分别为0.04、0.06和0.08，K1=3，K0为1、2、3、4和5时，本文算法在AWGN信道中的检测概率随信噪比变化曲线如图2(a)、(b)和(c)所示。

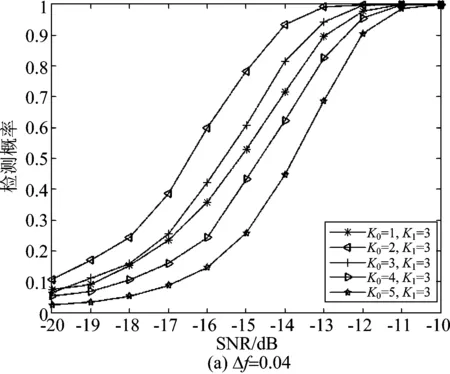
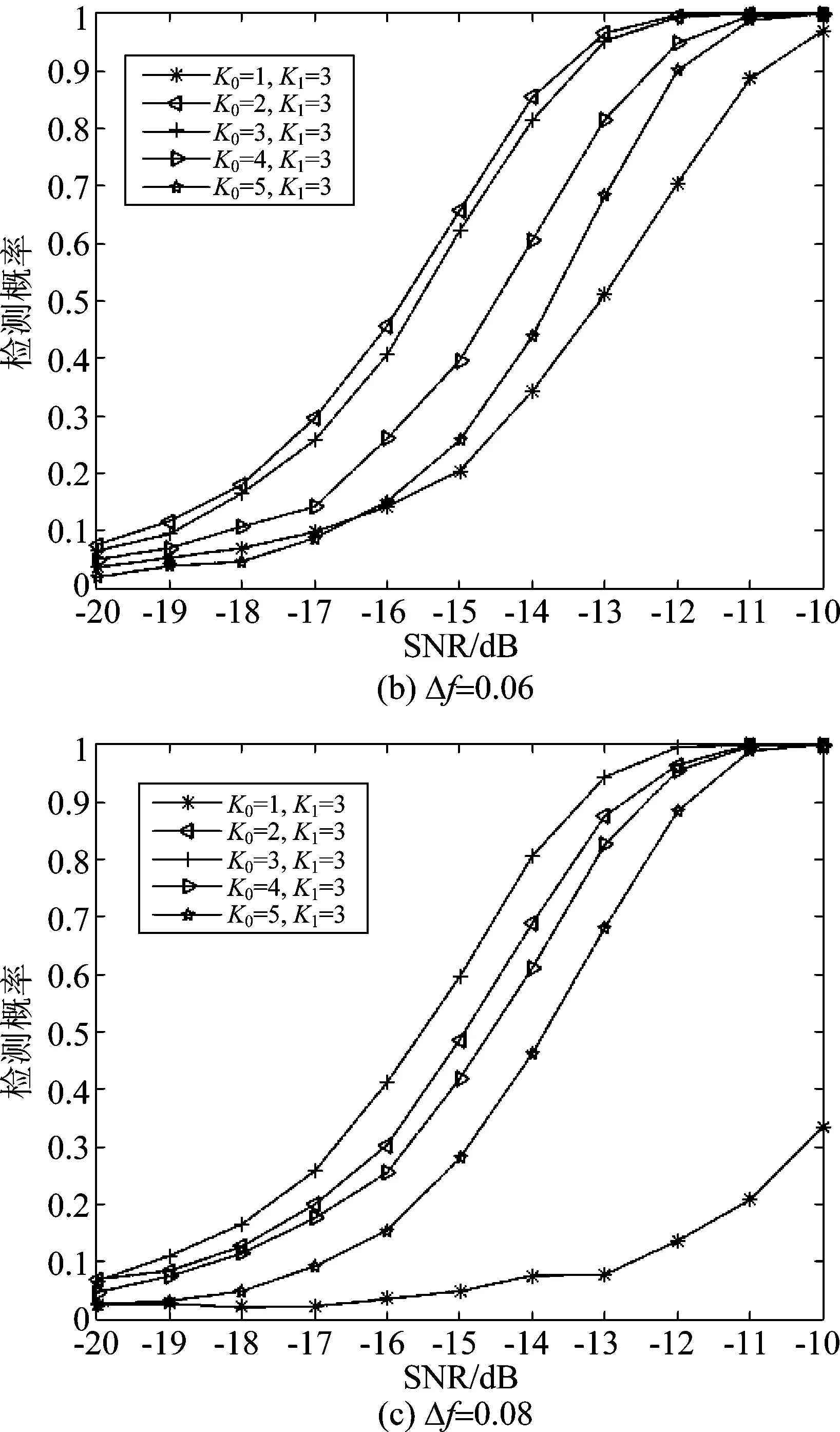
图2 Δf取不同值时，不同K0下的算法性能曲线

由图可见，随着Δf的增大，检测性能最优对应的K0值相对增大。由于Δf是随机且较小，因此K0取2至3。下面以Δf为0.06、K0取最佳值2，仿真分析其他参数影响及算法性能比较。

(4)不同帧长时算法性能比较。当频偏系数为Δf=0.06，Pf=0.01，码元数为500，帧长分别为M=16(K0=2，K1=3)和M=48(K0=2，K1=6)时，本文算法、PSRA算法和PSC算法在AWGN信道中的检测概率曲线如图3所示。其中实线和虚线分别表示M=16和M=48情况。由图可见，不同帧长情况下，本文算法检测概率大于PSC算法和PSRA算法。帧长太长用于功率谱估计帧数偏少，功率谱估计准确性下降，频谱感知性能就下降。下文取M=16。

(5)不同码元数时算法性能比较。频偏系数为Δf=0.06，Pf=0.01，码元数为250和500, 帧长M=16(K0=2，K1=3)时，本文算法、PSRA算法和PSC算法在AWGN信道的检测概率曲线如图4所示。

图3 AWGN信道中三种算法在不同帧长下的性能曲线

图4 AWGN信道中三种算法在不同码元数下的性能曲线

其中实线和虚线分别表示码元数为500和250的情况。由图可见，在不同码元情况下，本文算法检测概率大于PSC算法和PSRA算法，码元数越多算法性能越好。下文取码元数为500。

图5 噪声不确定度对算法影响

(7)算法的ROC(Receiver Operating Characteristics)曲线。频偏系数为Δf=0.06，码元数为500，帧长M=16(K0=2，K1=3)，信噪比为-13 dB时，三种算法在AWGN信道和Rayleigh衰落信道中的ROC曲线如图6(a)和(b)所示。实线和虚线分别表示ρ=1.0和1.1的情况。

由图可见，两种信道中，本文算法对噪声不确定度的鲁棒性优于PSC算法和PSRA算法，具有更优的抗噪声不确定性能力。

图6 三种算法的ROC曲线

4 结论

提出了一种基于功率谱的最大最小平均比值算法，推导了算法的检测门限表达式，该算法不受噪声不确定度的影响，当存在载波频偏时，本文算法的频谱感知性能要优于PSC算法和PSRA算法。

[1] Mitola J I, Maguire Q G. Cognitive radio: making software radios more personal[J]. IEEE Personal Communications, 1999, 6(4): 13-18.

[2] Patel A, Tripathi B, Jagannatham K A J. Robust Estimator-Correlator for Spectrum Sensing in MIMO CR Networks with CSI Uncertainty[C]∥IEEE Wireless Communications Letters, 2014, 3(3): 253-256.

[3] 龙颖贤,张宁,周峰,等. 一种基于噪声估计的能量检测自适应门限新算法[J]. 电信科学, 2012, 28(5): 49-53.

Long Yingxian, Zhang Ning, Zhou Feng, et al. A New Adaptive Threshold Algorithm Based on Noise Estimation for Energy Detection[J]. Telecommunications Science, 2012, 28(5): 49-53. (in Chinese)

[4] 卢光跃,弥寅,包志强. 特征值极限分布的改进合作频谱感知[J]. 信号处理, 2014,30(3): 261-267.

Lu Guangyue, Mi Yin, Bao Zhiqiang. Novel Cooperative Spectrum Sensing Based on Limiting Eigenvalue Distribution[J]. Journal of Signal Processing, 2014, 30(3): 261-267. (in Chinese)

[5] López-Valcarce R, Vazquez-Vilar G, Sala J. Multiantenna spectrum sensing for cognitive radio: overcoming noise uncertainty[C]∥2010 2nd IEEE International Workshop on Cognitive Information Processing (CIP), Elba, Italy, 2010: 310-315.

[6] Bomfin C D V R, Guimarães A D, De Souza A A R. On the probability of false alarm of the power spectral density split cancellation method[J]. IEEE Wireless Communication Letters, 2016, 5(2): 164-167.

[7] 孙哲. 特征值频谱感知算法的研究及改进[D]. 西安: 西安电子科技大学, 2014.

Sun Zhe. Research and Improvement on Eigenvalue Based Spectrum Sensing Algorithm[D]. Xi’an: Xidian University, 2014. (in Chinese)

[8] 齐佩汉, 司江勃, 李赞. 新型抗噪声不确定度谱分段对消频谱感知算法[J]. 西安电子科技大学学报, 2013, 40(6): 19-24.

Qi Peihan, Si Jiangbo, Li Zan. Novel anti-noise-uncertainty spectrum sensing algorithm based on power spectral density segment cancellation[J]. Journal of Xidian University, 2013,40(6): 19-24. (in Chinese)

[9] 齐佩汉, 司江勃, 李赞. 基于功率谱分段对消频谱感知算法研究及性能分析[J]. 电子与信息学报, 2014, 36(4): 769-774.

Qi Peihan, Si Jiangbo, Li Zan. Research and Performance Analysis of Spectrum Sensing Algorithm Based on the Power Spectral Density Segment Cancellation[J]. Journal of Electronics & Information Technology, 2014, 36(4): 769-774. (in Chinese)

[10] Gao Rui, Li Zan, Qi Peihan, et al. A robust cooperative spectrum sensing method in cognitive radio networks[J]. IEEE Communications Letters, 2014, 18(11): 1987-1990.

[11] 吕曦. 认知无线电中频谱感知算法的研究[D]. 杭州：杭州电子科技大学, 2017.

Lv Xi. Research on spectrum sensing algorithm in cognitive radio[D]. Hangzhou: Hangzhou Dianzi University, 2017. (in Chinese)

[12] Pascal C, Sri H M, Aren J, et al. Frequency offset correction in speech without detecting pitch[C]∥IEEE International Conference on Acoustics, Shanghai, China. 2013 :7020-7024.

[13] Fan S H, Yu J J, Qian D Y, et al. A Fast and Efficient Frequency Offset Correction Technique for Coherent Optical Orthogonal Frequency Division Multiplexing[J]. Journal of Lightwave Technology, 2011, 29(13): 1997-2004.

[14] 刘希孺. 数理统计引论[M]. 北京:科学出版社,1999.

Liu Xiru. Statistics Introduction[M]. Beijing: Science Press, 1999. (in Chinese)