通用滤波多载波通信系统中干扰抑制均衡算法

路 娟 何世文 黄永明 杨绿溪

(东南大学信息科学与工程学院, 江苏南京 210096)

1 引言

第五代移动通信系统(5G)将会支持更多的新兴应用,如物联网(Internet of Things, IoT)应用和机器通信应用(Machine Type Communication, MTC)等[1]。为支持5G中的新兴应用,5G系统的物理层空口设计需要具备以下特点[2-3]:首先,需要能够支持不同的帧结构。5G系统中的新兴应用各自具有不同的特点,需要不同的帧长度及载波宽度;其次,需要放松对时频同步的严苛要求。5G系统中将包含大量的MTC应用,在这类应用中将使用大量的传感器设备,这类设备造价较低,不能进行精确的时频同步,同时也不适合运行过复杂的算法;最后,在5G中将有大量的设备需要接入网络,频谱资源显得尤为重要。如何能够提高频谱利用率,合理利用零散频谱将显得尤为重要。为实现以上需求,一种有效的解决方案是对载波技术进行研究和改进。

正交频分复用(OFDM)能够利用IFFT和FFT运算快速地实现调制和解调,被广泛应用于各种通信系统之中,如无线局域网(Wireless Local Area Network,WLAN),长期演进(Long Term Evolution,LTE)系统等。但OFDM调制使用矩形脉冲成型,其频域表现为sinc函数,带外功率泄露较大,对载波间干扰(Inter Carrier Interference,ICI)敏感,因此对时频同步要求严格;同时在OFDM系统中需要添加循环前缀作为保护间隔来避免多径信道所带来的干扰,不能最大化频谱利用率[4]。为满足5G应用的新需求,学者们提出了多种新型多载波技术。

5G中的新型多载波技术主要分为三类:子载波滤波多载波、子带滤波多载波及它们的变形。子载波滤波多载波的典型代表为滤波器组多载波(Filter Bank Multi-carrier,FBMC)和广义频分复用(General Frequency Division Multiplexing,GFDM);子带滤波多载波的典型代表为滤波OFDM(Filter-OFDM,F-OFDM)和通用滤波多载波(Universal-filtered Multi-carrier,UFMC)。

在FBMC中,子载波频谱仅和相邻子载波重叠,因此能够节约频谱资源。但为了实现这一目标,子载波滤波器的长度通常需要为OFDM符号长度的若干倍[5];通常情况下FBMC的子载波频谱相互重叠,为消除相邻载波间的干扰,进一步提高频谱利用率需要和OQAM 技术结合,而OQAM的使用使FBMC难以和MIMO技术结合[5]。

在GFDM中,为避免滤波器拖尾,采用了循环脉冲成型滤波,同时GFDM调制以块为单位进行[6]。但其循环脉冲成型会在块内引起符号间干扰(Inter Symbol Interference,ISI)和ICI,接收端需要使用复杂度较高的均衡算法[7]。

在F-OFDM中,调制参数(如子载波间隔)被设计为是可变的。一个频带可以被分为若干个子带,根据应用的特点,每个子带可以选用不同的调制参数[8]。当系统中存在由不同调制参数生成的子带信号时,这些子带信号不再相互正交,彼此会产生干扰[9],需要使用子带滤波器来避免干扰。

与OFDM相同,UFMC子载波间隔也是固定的,其子带滤波器的引入是为了降低子带外的功率泄露。UFMC中的滤波器应用在子带上,因此滤波器长度较短,适合5G中大量的MTC应用;同时可以利用IFFT和FFT运算快速地实现调制和解调,被认为是5G多载波技术强有力的候选对象[4]。

UFMC作为5G多载波技术强有力的候选对象,对其进行研究具有重要的意义和价值。现有的文献大多着重于对UFMC系统的性能进行分析[10-13],缺少能够推动其在实际系统中应用的文章。文献[10]和[11]分析了在多径信道下,载波频偏对UFMC系统性能的影响。文献[12]和[13]分析对比了UFMC和OFDM的带外功率,说明通过子带滤波器的使用UFMC能够减少带外功率泄露。

5G通信系统中将包含大量的IoT通信业务, MTC是IoT的重要场景之一。MTC主要涉及两种通信类型:一种是MTC设备与一个或多个MTC服务器之间的通信;另一种是MTC设备与设备之间的通信[14]。MTC的主要表现形式为各种传感器设备进行数据信息的采集和传输,通常收发两端的位置相对固定的,信道时变性较慢。本文对慢时变信道条件下,UFMC系统中的信道估计和均衡方案进行了研究。信道估计算法通常分为时域信道估计算法和频域信道估计算法,在OFDM中循环前缀的使用能够将信道和信号的线性卷积转换为循环卷积,因此OFDM系统中使用的是频域信道估计算法。OFDM系统中的信道估计主要分为导频辅助的估计和盲信道估计,盲信道估计需要较多的训练符号且复杂度高,因此实际系统(如LTE、WLAN)中使用的是导频辅助的估计算法,如LS[15]、MMSE[16]、LMMSE[17]。与LS算法相比,MMSE算法能够获得更好的性能,但需要事先得到信道的相关矩阵和噪声方差,同时复杂度较高;与MMSE算法相比,LMMSE算法通过使用信道的频域相关矩阵降低了MMSE算法的实现复杂度。由于相邻UFMC符号间没有循环前缀,因此OFDM系统中的信道估计算法不能直接适用于UFMC系统。为降低信道估计实现的复杂度,本文将借助导频符号进行信道估计。文献[18]中的信道估计算法忽略了多径信道所带来的ICI、IBI和ISI,估计出的频域信道信息存在较大的误差;而文献[19]中的信道估计算法假设了相邻UFMC符号间有足够的ZP(Zero Padding)作为保护间隔,在接收端利用2N点FFT进行频域信道信息估计,该算法需要使用2N点FFT,复杂度较高,并且需要添加ZP,将占用较多的传输资源。

本文首先对通用滤波多载波在慢时变多径信道下的性能进行了分析;其次提出适用于该多载波系统的信道估计方案,该方案设计了具有重复样式的导频结构并利用N/ 2点的FFT变换进行信道估计,算法复杂度较低,同时不需要添加额外的ZP,能够节约传输资源;最后提出基于干扰消除的Zero-Forcing均衡算法和基于迭代干扰消除的均衡算法。仿真结果表明,本文提出的信道估计和均衡算法能有效消除通用滤波多载波在多径信道下所经受的ISI、ICI和IBI,提升其在多径信道下的性能。

2 UFMC系统模型

令si=[si(0),…,si(k),…,si(N-1)]T表示第i个待发送的复数符号,其中si(k)表示第k个子载波上的发送数据。如图1所示,待发送的数据被分为B个子带分别进行N点IFFT变换,经并/串转换后再经各子带滤波器进行子带滤波,最后各子带上的数据被叠加在一起通过射频发送至无线信道。

为简单其见,令N1=N2…=NB=M(MB=N),即各子带大小相同。各子带滤波器可以通过将原型滤波器进行频谱搬移得到,具有相同的长度。本文假设所有子带滤波器长度均为L,且第j个子带滤波器的系数为{fj(0)fj(1) …fj(L-1)}。经UFMC调制后得到的符号长度NU=N+L-1。令xi=[xi(0),xi(1),…,xi(NU-1)]T表示第i个UFMC符号,则有:

(1)

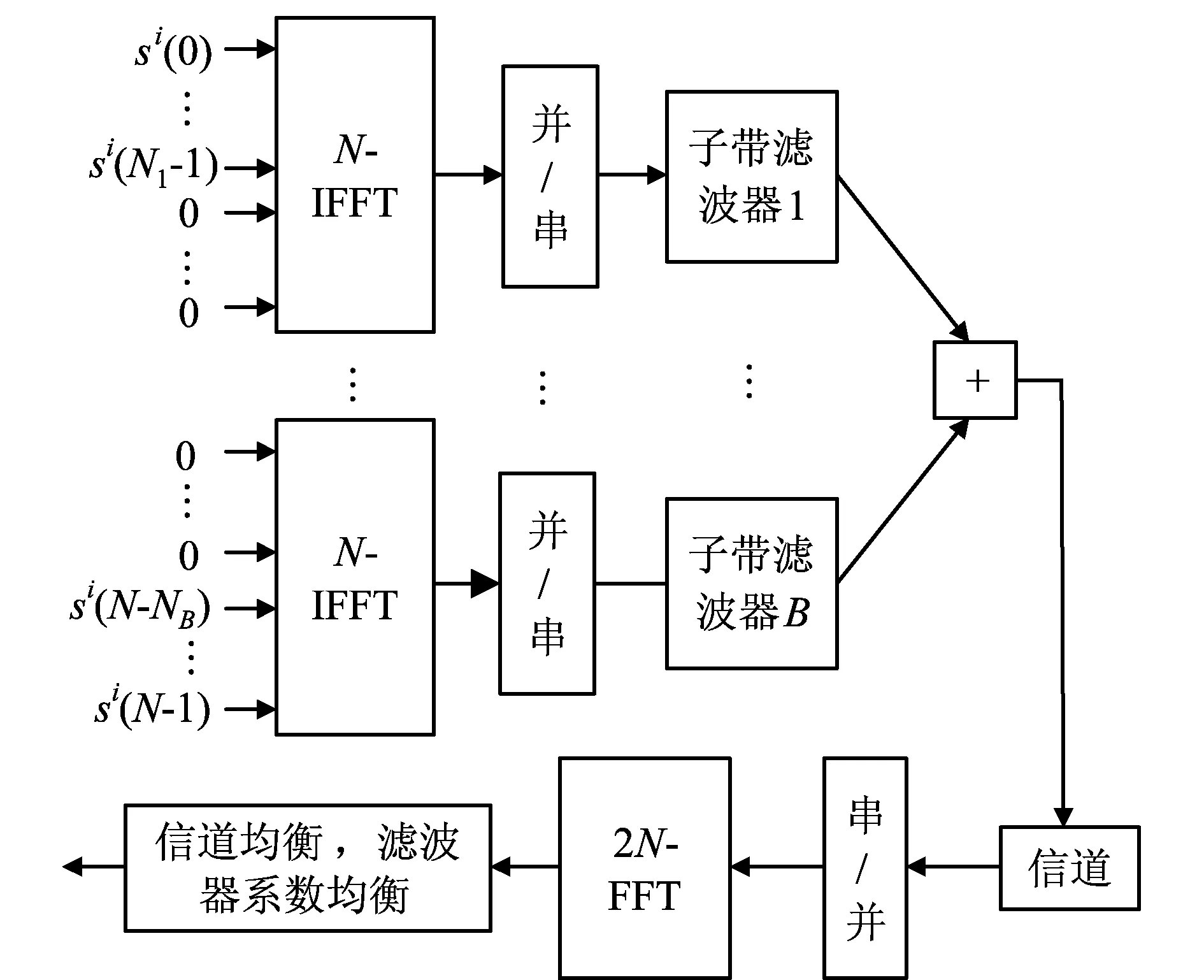
图1 UFMC系统模型图Fig.1 UFMC system structure

本节对UFMC的系统模型进行了介绍,接下来的章节将定量分析多径信道对UFMC系统的影响,并对适用于UFMC系统的信道估计和均衡方案进行研究。

3 信道影响分析

在OFDM系统中为消除多径信道带来的影响,两个连续的符号之间需要插入保护间隔,可以通过插入ZP或循环前缀(Cyclic Prefix,CP)实现。而在UFMC系统中,相邻符号没有添加CP或ZP就直接被发送至无线信道。在本文中假设信道为慢时变信道,信道在同一帧时间内近似不变,而在不同帧之间的变化相互独立。在5G系统中由于通信业务的多样性使得帧结构设计与4G LTE相比更加复杂,目前还没有国际标准来定义5G的帧结构,但有一点已达成共识——5G的子帧长度明显比4G LTE短[20]。本文假设信道长度为Lh且Lh-1≤NU(即多径信道仅影响相邻UFMC符号[注]当Lh-1>NU时,多径信道将影响多个UFMC符号。),多径信道的系数为{h(0)h(1) …h(Lh-1) }。如图2所示,当经过多径信道后,接收端的第i个UFMC符号将遭受两种干扰:第一种干扰来自第i-1个符号在信道作用下的拖尾;第二种干扰来自第i个符号自身的截断,一部分符号信息被丢失。

图2 UFMC经过多径信道示意图Fig.2 UFMC symbol through the multipath channel

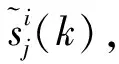
(2)

为定量分析多径信道对UFMC性能的影响,将yi表示为:

yi=H1xi+H2xi-1+ni

(3)

在式(3)中,xi-1=[xi-1(0),xi-1(1),…,xi-1(NU-1)]T为第i-1个UFMC符号。H1和H2均为由信道系数组成的矩阵,两者的大小均为NU×NU。H2xi-1表示由多径信道带来的来自第i-1个UFMC发送符号的ISI。ni表示噪声矢量。

H2=

(4)

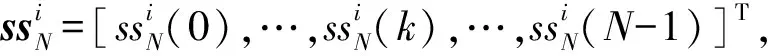
0≤k≤N-1

(5)

其中:

(6)

(7)

(8)

(9)

h(N+L-1+n-l)fj(l-m)

(10)

4 信道估计及均衡方案设计

4.1 信道估计

为消除多径信道所带来的ISI、ICI和IBI,本小节提出一种简单易行的信道估计方案,该方案利用具有重复结构的导频进行信道估计。

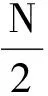
(11)

图3 导频过滤波器前后变化Fig.3 Pilot’s change before and after sub-band filter

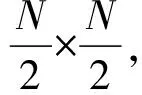
进一步可以得到:

(12)

4.2 信道均衡

(1) 基于干扰消除的Zero-Forcing均衡算法

为提高UFMC在多径信道下的性能,本文提出一种基于干扰消除的Zero-Forcing均衡算法。UFMC在多径信道下遭受的ISI主要来自上一个UFMC符号,而其遭受的ICI和IBI主要来自符号内部。为实现该均衡算法,将xi表达为式(13)所示,yi表达为式(14)所示。在式(13)和(14)中,F是大小为NU×(NB)的矩阵,F=[F1F2…FB];V是大小为(NB)×N的矩阵,V=diag(V1,…,Vj,…,VB),其中Vj大小为N×M,是由N点IFFT矩阵WN的第(j-1)M+1至jM列组成的矩阵。

xi=FVsi

(13)

yi=H1FVsi+H2FVsi-1+ni

(14)

为消除ISI、ICI和IBI,本小节提出的基于干扰消除的Zero-Forcing均衡算法包含的主要步骤如下:

1)利用本文4.1节所述的信道估计算法进行信道估计,得到时域的信道系数。

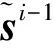
(15)

(16)

(2)基于迭代干扰消除的均衡算法

从第3节的分析中可以看出ICI和IBI由UFMC符号自身的截断造成。如图2所示,第i个UFMC发送符号在多径信道的作用下会有一部分数据被扩散至第i+1个接收符号中产生ISI,而第i个接收符号则会因为丢失该部分数据而形成ICI和IBI。因此本小节提出一种基于迭代干扰消除的均衡算法,在消除ISI的基础上,通过迭代补偿接收符号所丢失的数据逐步消除ICI和IBI。此算法包含的主要步骤如下:

步骤 1利用本文4.1节所述的信道估计算法进行信道估计,得到时域的信道系数。

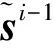
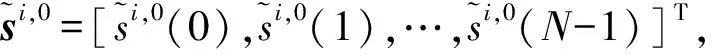
(17)

步骤 5令l=l+1,如果l>Imax则迭代终止,否则继续执行步骤4中的操作。

5 仿真结果

本节通过仿真的方法验证本文所提出的信道均衡算法以及信道估计算法的性能。仿真参数设计为:FFT大小为128,子带大小为12,子带个数为9,第0～4号和123～127号子载波上不发送数据;调制方式为4QAM;子带滤波器的类型为Dolph-Chebyshev滤波器,其旁瓣衰减为40 dB,长度为11;仿真使用的多径信道的抽头时延为[0 3 5 6 8],各个抽头对应的抽头功率(dB)为[0 -8 -17 -21 -25]。

多径信道下UFMC和OFDM的误码率(Symbol Error Rate,SER)随信噪比的变化曲线如图4所示。从中可以看出在低信噪比时UFMC和OFDM性能相近,此时噪声对两者的性能影响较大。而当信噪比较高时,UFMC的误码率比OFDM更大,此时UFMC所经受的ISI、ICI和IBI成为影响UFMC性能的主要因素。图5为在信噪比为25 dB时,UFMC各子载波上所经受的ISI、ICI和IBI的相对大小,从中可以看出子载波所经受的ICI和IBI要高于ISI。

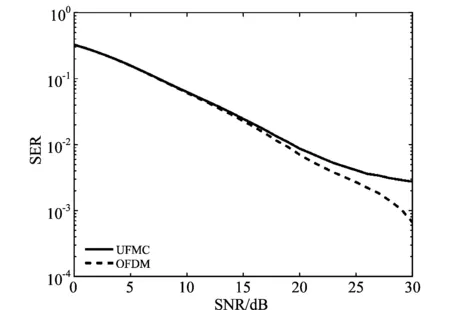
图4 UFMC和OFDM在多径信道下性能比较Fig.4 Performance comparison of UFMC and OFDM under multipath channel

多径信道下UFMC各种均衡算法的性能如图6所示。图6中分别比较了基于2N点FFT的频域单点均衡算法[10-11,18]、消除ISI的2N点FFT频域单点均衡算法,本文所提出的基于干扰消除的Zero-Forcing均衡算法及基于迭代干扰消除的均衡算法在不同信噪比下的误码率大小。从图6可以看出,基于2N点FFT的频域单点均衡算法的性能最差,而本文提出的基于干扰消除的Zero-Forcing均衡算法具有最好的性能。基于迭代干扰消除的均衡算法可以在一定程度上消除ISI、ICI和IBI干扰,但在迭代过程中由于均衡得到的信号中已经包含干扰,所以性能不如基于干扰消除的Zero-Forcing均衡算法。

图5 各子载波上的ISI和ICI、IBI大小Fig.5 Estimation and comparison of ISI、ICI and IBI on each subcarrier

图7显示了在使用不同的信道估计和均衡算法后,UFMC在多径信道下的误码率随信噪比的变化。与文献[18]中的信道估计和均衡算法作相比(即为频域单点信道估计和均衡所对应的曲线),本文所提出的信道估计和均衡方案具有更好的性能,其中采用了本文所提出的信道估计算法和基于干扰消除的Zero-Forcing均衡算法的性能最好。

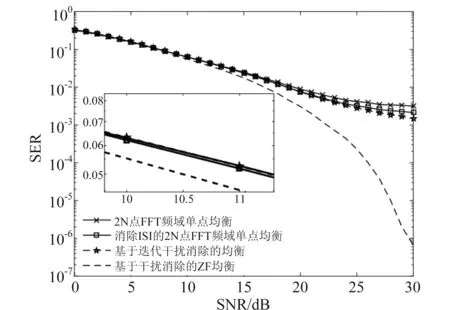
图6 各种均衡算法性能比较Fig.6 Performance comparison of various equalization algorithms

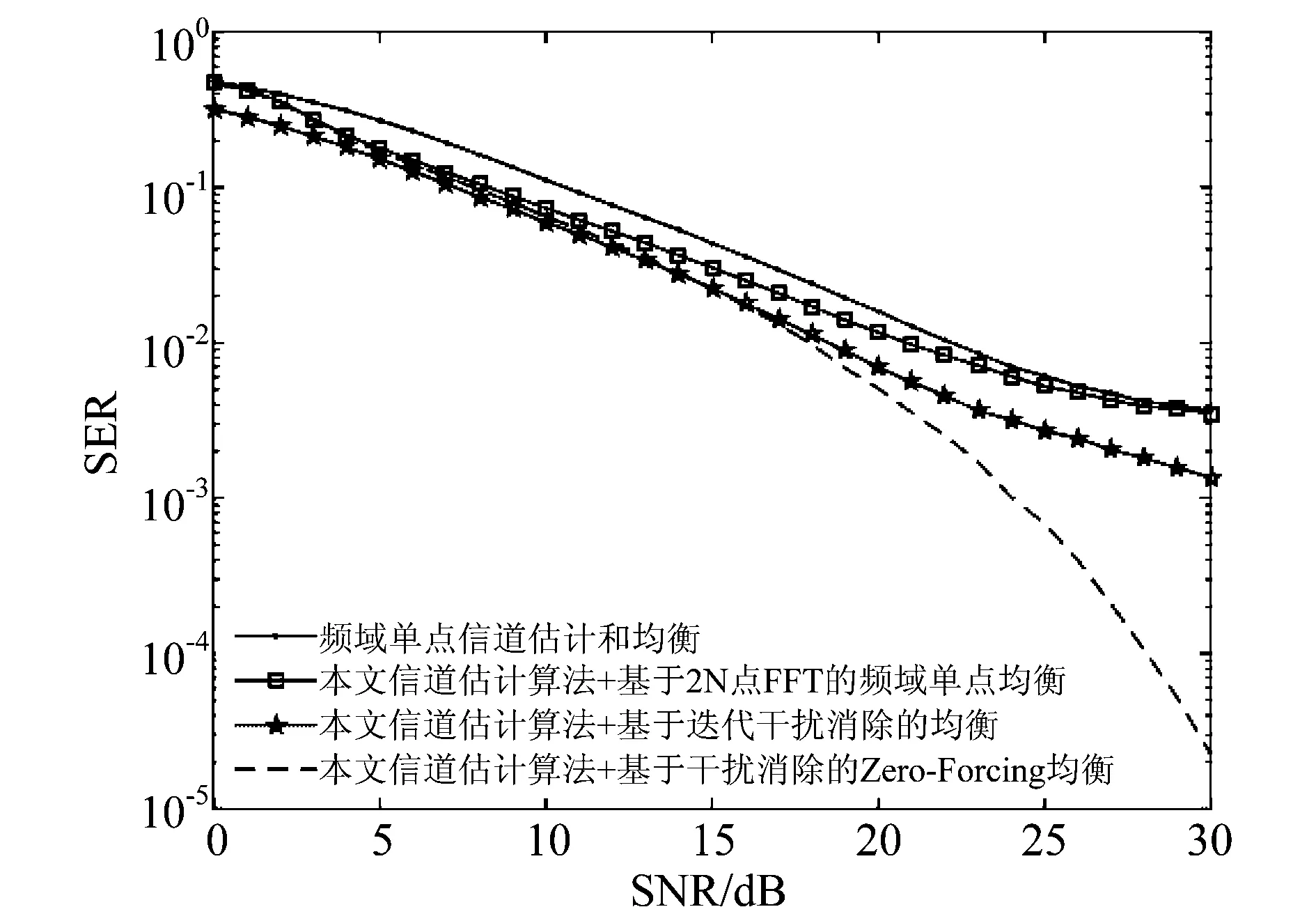
图7 不同信道估计和均衡算法性能比较Fig.7 Performance comparison of various equalizationalgorithms based on estimated channel

6 结论

本文分析了UFMC在多径信道下的性能,并提出适用于该多载波的信道估计和均衡方案,为UFMC在实际系统中应用打下了基础。所提出的信道估计方案简易可行,同时基于干扰消除的Zero-Forcing均衡方案能有效地提升UFMC系统在多径信道下的性能。

[1] Series M. IMT Vision-Framework and overall objectives of the future development of IMT for 2020 and beyond[J]. Radiocommunication Sector of ITU, 2015.

[2] Andrews J G, Buzzi S, Choi W, et al. What will 5G be?[J]. IEEE Journal on Selected areas in Communications, 2014, 32(6): 1065-1082.

[3] Wunder G, Jung P, Kasparick M, et al. 5GNOW: non-orthogonal, asynchronous waveforms for future mobile applications[J]. IEEE Communications Magazine, 2014, 52(2): 97-105.

[4] Cho H, Yan Y, Chang G K, et al. Asynchronous Multi-User Uplink Transmissions for 5G with UFMC Waveform[C]∥Wireless Communications and Networking Conference (WCNC), 2017 IEEE. San Francisco, CA, USA: IEEE, 2017: 1-5.

[5] Bellanger M, Le Ruyet D, Roviras D, et al. FBMC physical layer: a primer[J]. PHYDYAS, 2010, 25(4): 7-10.

[6] Tang N, He S, Xue C, et al. Iq imbalance compensation for generalized frequency division multiplexing systems[J]. IEEE Wireless Communications Letters, 2017, 6(4): 422- 425.

[7] Gaspar I, Michailow N, Navarro A, et al. Low complexity GFDM receiver based on sparse frequency domain processing[C]∥Vehicular Technology Conference (VTC Spring), 2013 IEEE 77th. Dresden, Germany: IEEE, 2013: 1- 6.

[8] Zhang X, Jia M, Chen L, et al. Filtered-OFDM-enabler for flexible waveform in the 5th generation cellular networks[C]∥Global Communications Conference (GLOBECOM), 2015 IEEE. San Diego, CA, USA: IEEE, 2015: 1- 6.

[9] Zhang L, Ijaz A, Xiao P, et al. Filtered OFDM Systems Algorithms and Performance Analysis for 5G and Beyond[J]. IEEE Transactions on Communications, November, 2017, PP(99): 1-1.

[10] 田广东,王珊,段思睿,等.UFMC系统在多径衰落信道中的干扰消除[J].电讯技术,2017,57(3): 335-340．

Tian Guangdong, Wang Shan, Duan Sirui, et al. Interference suppression of universal filtered multicarrier system in multipath fading channel[J]．Telecommunication Engineering, 2017, 57(3): 335-340. (in Chinese)

[11] 麻超,张晓瀛,习勇,等．多径时变信道中存在频偏的 UFMC 系统性能分析[J]．通信技术,2017,50(7): 1357-1361．

Ma Chao,Zhang Xiaoying, Xi Yong, et al. Performance Analysis of UFMC Systems with Residual Carrier Frequency Offset over Multipath Time-Varying Channels[J]. Communications Technology, 2017,50(7): 1357-1361．(in Chinese)

[12] Bochechka G, Tikhvinskiy V, Vorozhishchev I, et al. Comparative analysis of UFMC technology in 5G networks[C]∥Control and Communications (SIBCON), 2017 International Siberian Conference on. Astana, Kazakhstan: IEEE, 2017: 1- 6.

[13] Kishore K K, Umar P R, Naveen V J. Comprehensive Analysis of UFMC with OFDM and FBMC[J]. Indian Journal of Science & Technology, 2017, 10(17):1-7.

[14] 宫诗寻, 陶小峰. 5G 大规模机器类通信中的传输技术[J]. 中兴通讯技术, 2017, 23(3): 20-23.

Gong Shixun, Tao Xiaofeng. Transmission Technologies in Massive Machine Type Communication for 5G[J]. ZTE Technology Journal, 2017, 23(3): 20-23.(in Chinese)

[15] Coleri S, Ergen M, Puri A, et al. Channel estimation techniques based on pilot arrangement in OFDM systems[J]. IEEE Transactions on Broadcasting, 2002, 48(3): 223-229.

[16] Van De Beek J J, Edfors O, Sandell M, et al. On channel estimation in OFDM systems[C]∥Vehicular Technology Conference, 1995 IEEE 45th.Chicago, IL, USA: IEEE, 1995, 2: 815- 819.

[17] Edfors O, Sandell M, Van de Beek J J, et al. OFDM channel estimation by singular value decomposition[J]. IEEE Transactions on Communications, 1998, 46(7): 931-939.

[18] Wang X, Wild T, Schaich F, et al. Pilot-aided channel estimation for universal filtered multi-carrier[C]∥Vehicular Technology Conference (VTC Fall), 2015 IEEE 82nd.Boston, MA, USA: IEEE, 2015: 1-5.

[19] Zhang L, He C, Mao J, et al. Channel Estimation and Optimal Pilot Signals for Universal Filtered Multi-carrier (UFMC) Systems[C]∥28th PIMRC Workshop 2017 Proceedings.Montreal, QC, Canada: IEEE, 2017.

[20] Pedersen K I, Berardinelli G, Frederiksen F, et al. A flexible 5G frame structure design for frequency-division duplex cases[J]. IEEE Communications Magazine, 2016, 54(3): 53-59.

[21] Raghavendra M R, Giridhar K. Improving channel estimation in OFDM systems for sparse multipath channels[J].IEEE Signal Processing Letters,2005,12(1):52-55.

[22] Li H, Liu D, Li J, et al. Channel order and RMS delay spread estimation with application to AC power line communications[J]. Digital Signal Processing, 2003, 13(2): 284-300.