多跳频信号的2D-DOA估计
2018-08-20杨银松于欣永东润泽
杨银松 郭 英 于欣永,2 李 雷 东润泽
(1. 空军工程大学信息与导航学院, 陕西西安 710077; 2. 空军通信士官学校, 辽宁大连 116100)
1 引言
跳频通信具有良好的抗干扰性、低截获性及强组网能力,在军事通信中得到广泛应用,也给通信对抗侦察带来了严峻挑战[1]。网台分选是跳频信号侦察的一个关键步骤,它可以从复杂的电磁环境中分选出跳频网台,为电子对抗实施精确干扰或恢复信息提供支援,同时也可以达到对抗跳频跟踪干扰的目的。
信号波达方向(DOA)在跳频信号网台分选中发挥着重要作用,也一直是研究的热门领域。文献[2- 4]最早提出空时频的概念,并将空时频处理方法用于非平稳信号的DOA估计和盲源分离中,性能优于传统方法;文献[5- 6]将空时频分析法引入跳频信号DOA估计,先用多向滤波器组得到清晰稳算法估计出DOA,为跳频信号DOA估计提出了新的思路,即先将宽带跳频信号简化为窄带信号,但是MUSIC算法需在参数空间进行谱峰搜索,占用大量的计算资源,并且没有考虑二维DOA情况,无法定位三维空间目标;文献[7- 8]在文献[5- 6]的基础上,引入极化信息,提出基于空间极化时频分布与ESPRIT算法结合的跳频信号二维DOA估计算法,既避免了峰值搜索,又能实现三维空间目标的定位,但是该算法存在复数域特征值求根以及参数配对问题,计算复杂度仍然较高;文献[9]在MUSIC算法的基础上,利用噪声子空间降维的思想构造空间谱,最后通过半谱搜索实现DOA估计,计算复杂度相比MUSIC算法降低了一半;文献[10]考虑到实际应用中天线阵列存在分布不均匀的情况,提出了基于随机布局天线的跳频信号DOA估计算法,但是计算过程过于复杂;文献[11]比较了LS-ESPRIT算法、TLS-ESPRIT算法和酉ESPRIT算法在W-CDMA中的DOA估计性能,得到酉ESPRIT算法在信噪比大于0 dB时,估计性能最优;文献[12-17]提出将酉 ESPRIT算法用于MIMO雷达的DOA估计,该算法将接收数据从复数运算转化为实数运算,克服了ESPRIT算法在低信噪比、低快拍数据的情况下,存在估计精度不高、需要参数配对的问题,并且文献[12]、[16]仿真结果均表明,与ESPRIT算法相比,酉ESPRIT算法的DOA估计精度更高,运算处理时间更短;文献[18]将酉ESPRIT算法用于跳频信号的一维DOA估计,高信噪比下估计性能好于LS-ESPRIT算法,但是存在低信噪比下估计性能差且鲁棒性也较差的问题。
综合以上问题,本文提出一种基于酉ESPRIT算法的多跳频信号2D-DOA估计算法。首先建立平面天线阵列接收模型并据此推导建立跳频信号的阵列快拍数据模型; 然后在时频分析过程中采用形态学滤波的方法对时频图修正,提高算法在低信噪比下的鲁棒性能,并基于修正的时频图将跳频信号分解为一个个有效hop;在此基础上,任取某一有效hop进行分析,采用酉ESPRIT算法完成跳频信号2D-DOA估计。
2 跳频信号的阵列快拍数据模型
假设跳频信号sn(t)的跳周期为Tn,在观测时间Δt内总共有L个跳,并且第l跳(l=1,2,...,L)的载频为wnl,初始相位为φnl,起始那个非完整跳在观测时间内的持续时长为Δt0n,则跳频信号sn(t)的数学表达式可描述为[8]
(1)
其中,νn(t)是跳频信号sn(t)的基带复包络;t′=t-(k-1)Tn-Δt0n为瞬时刻;rect表示单位矩形窗函数。
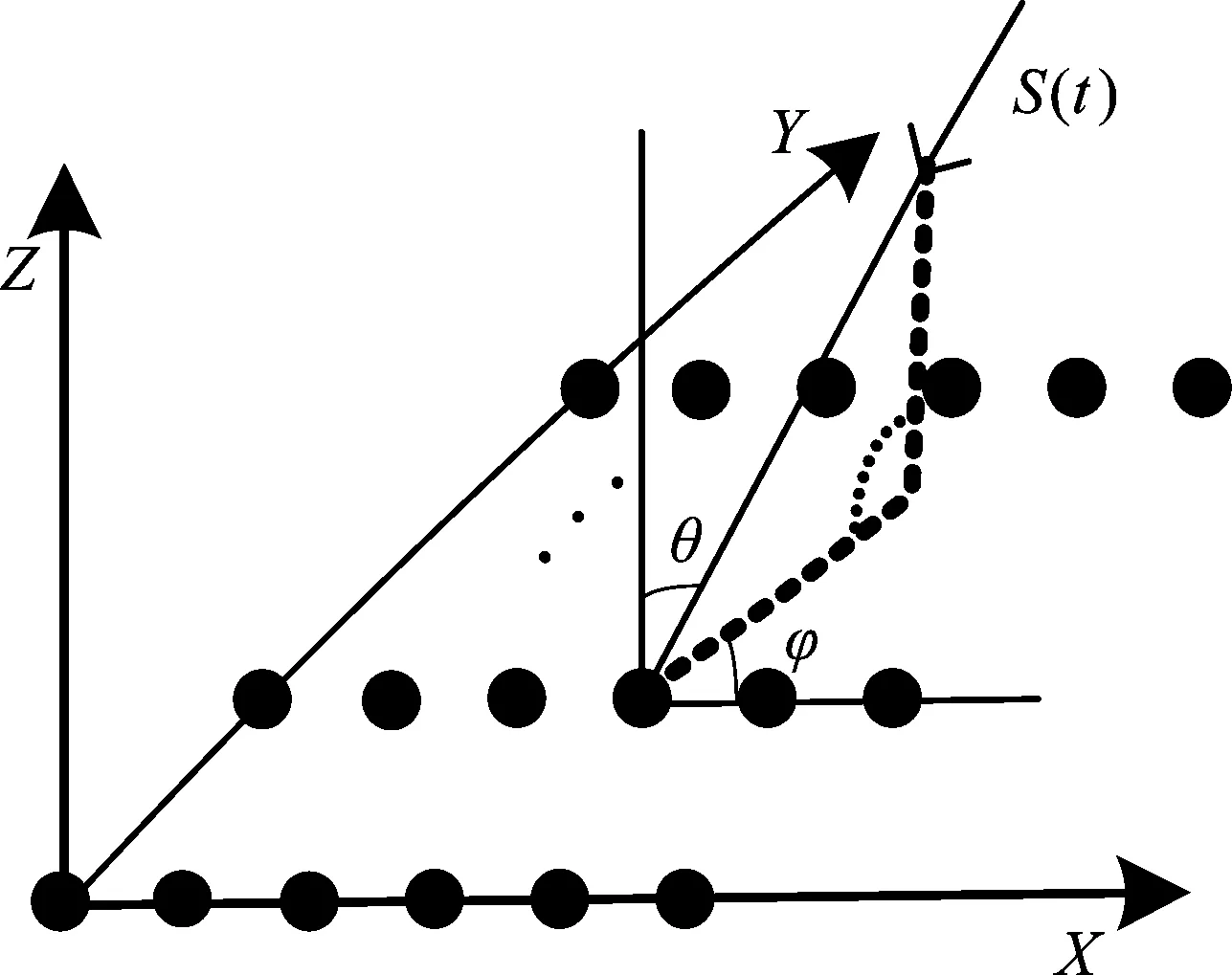
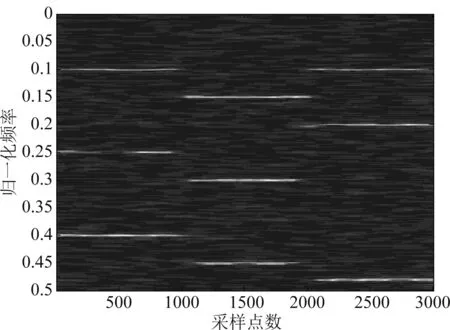
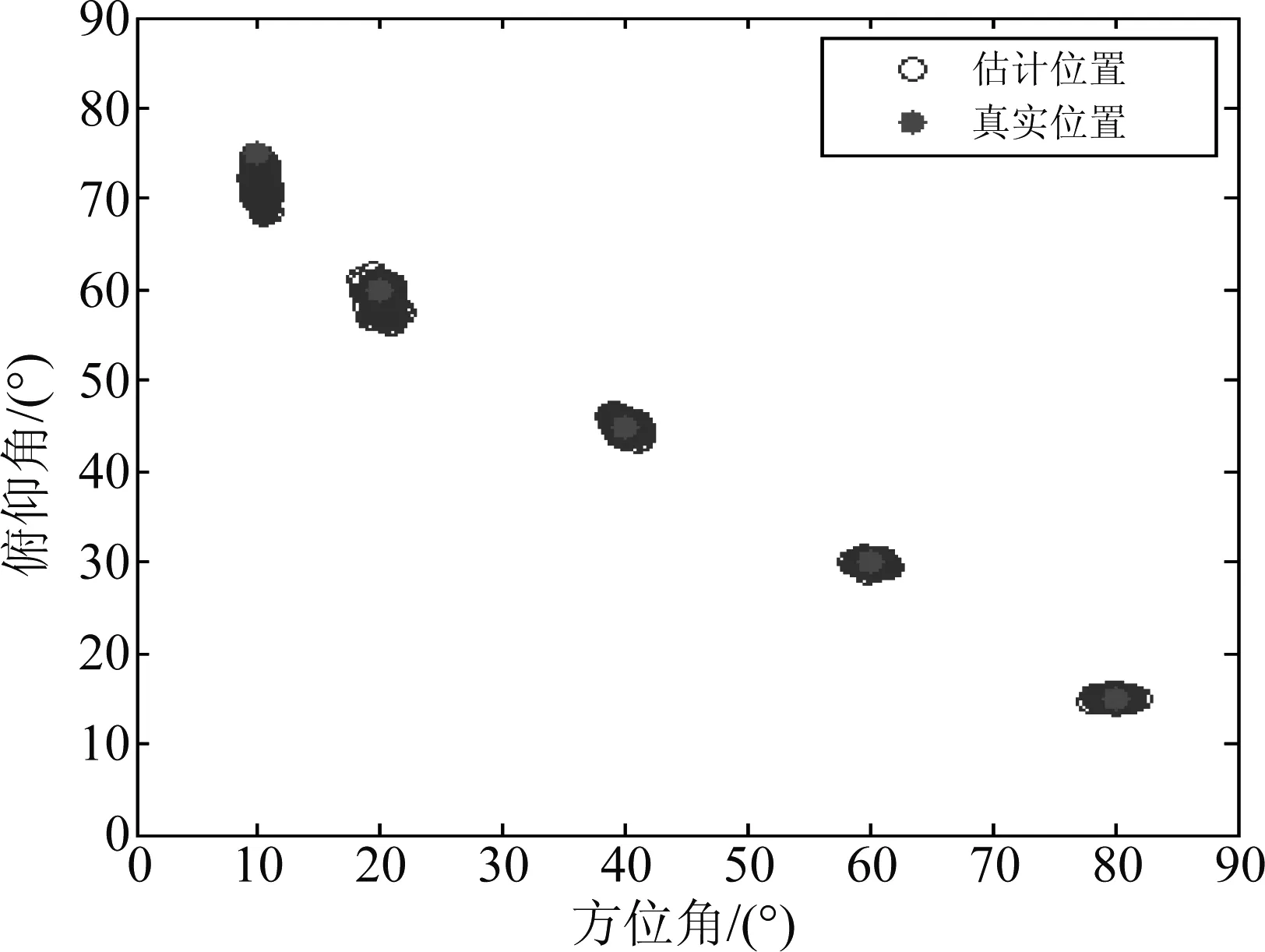
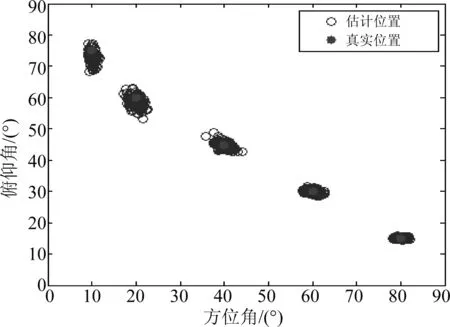
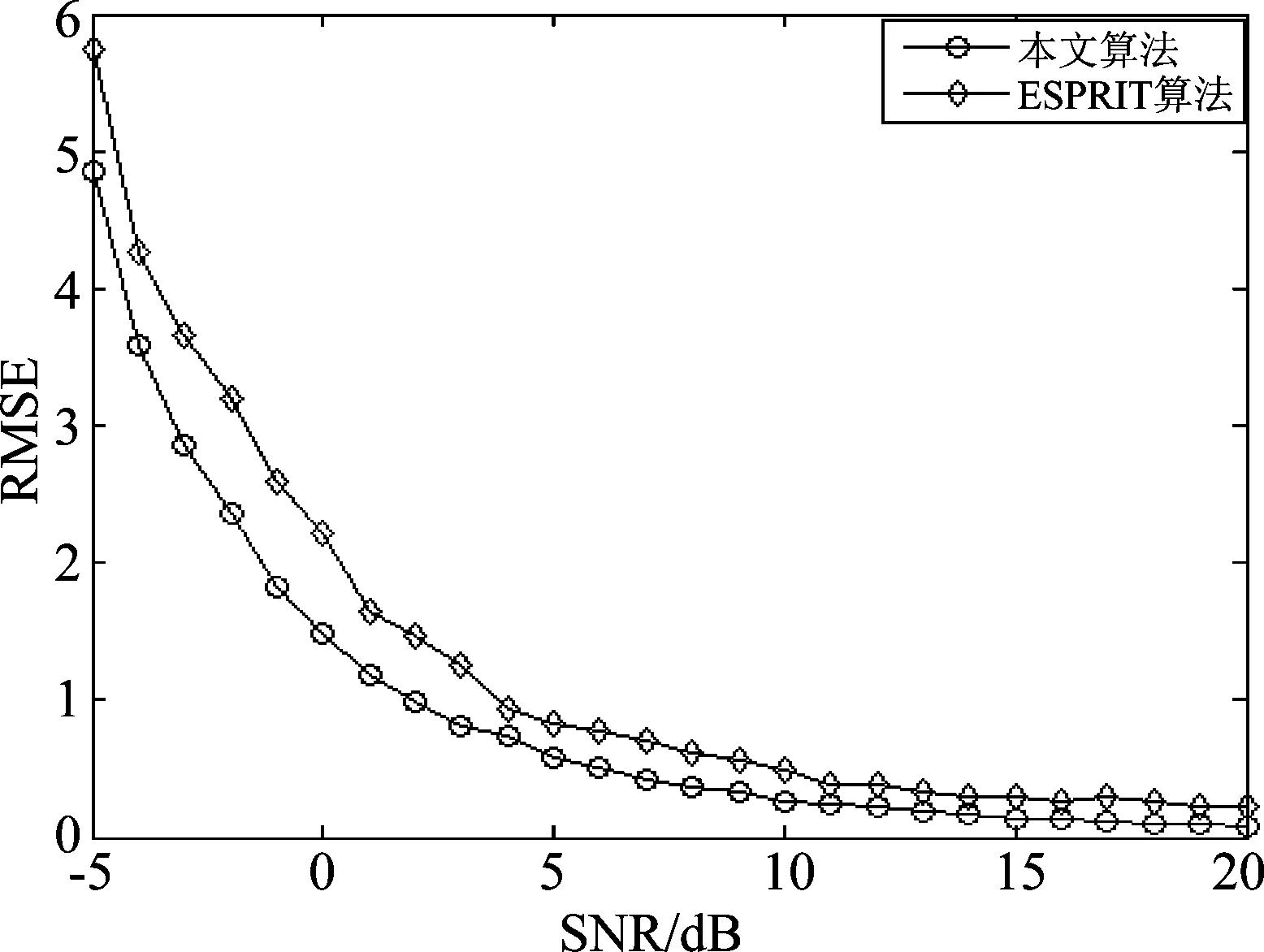
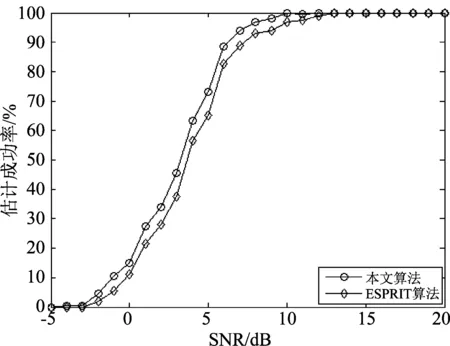
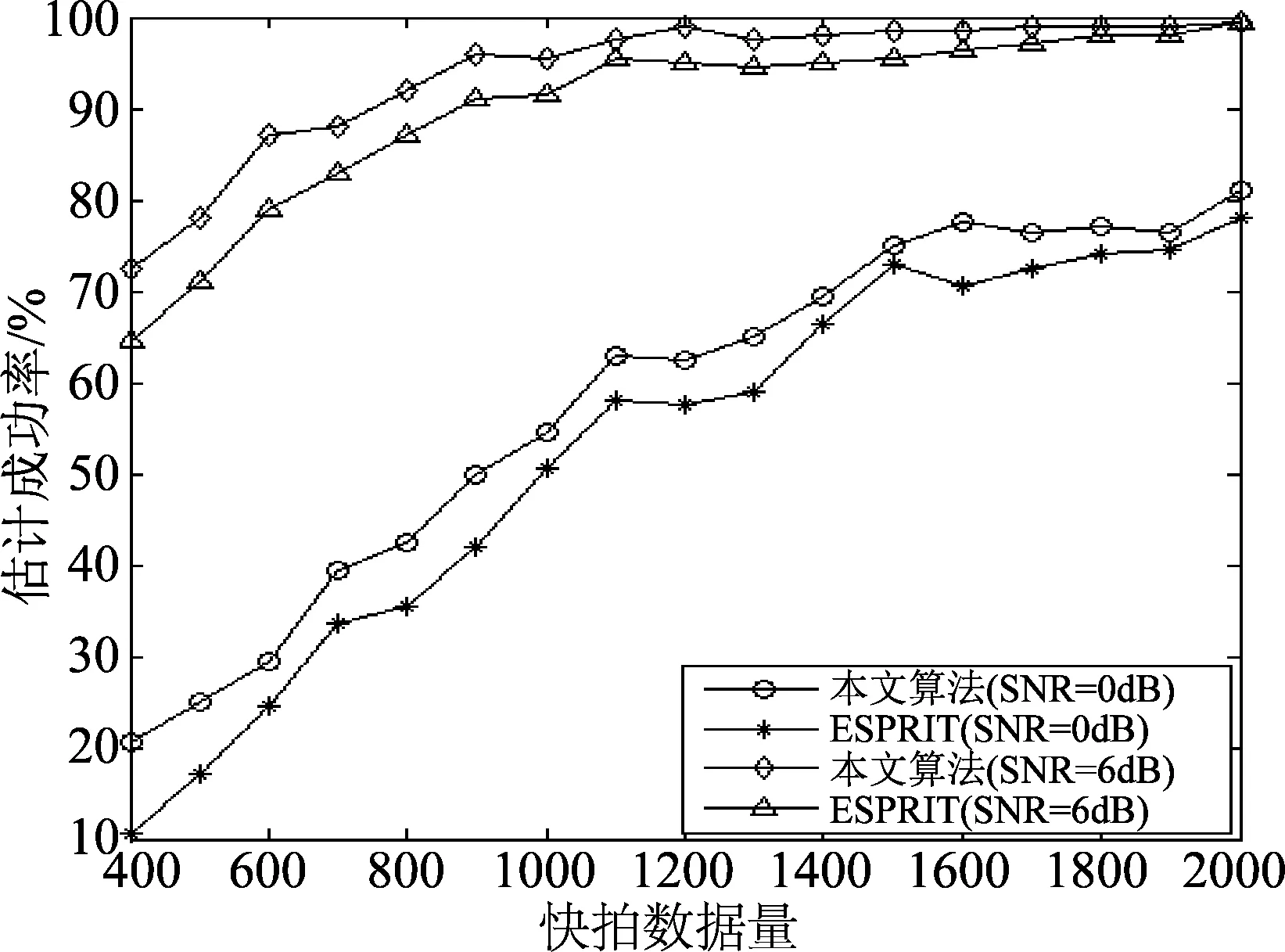
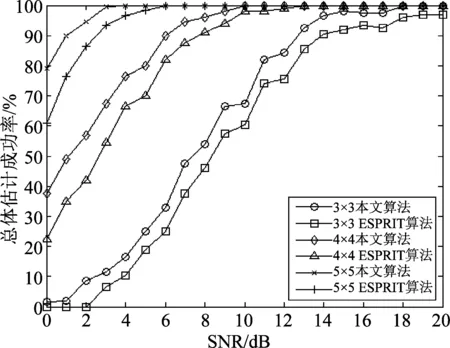
阵列结构如图1所示,阵元总数为N×M个,相邻阵元间距分别为d1、d2,并且满足max(d1,d2) 图1 N×M平面阵列Fig.1 The planar array of N×M 图2 信号波达方向示意图Fig.2 The 2D-DOA of FH signals 定义坐标原点阵元为参考阵元,X轴上N个阵元对应的方向矩阵为[17] Ax=[a1(θ1,φ1),a2(θ2,φ2),...,aK(θK,φK)] (2) 其中,ak(θk,φk)=[1,ej2πd1cos φksin θk/λ,...,ej2πd1(N-1)cos φksin θk/λ]T。Y轴上M个阵元对应的方向矩阵为 Ay=[b1(θ1,φ1),b2(θ2,φ2),...,bK(θK,φK)] (3) 其中,bk(θk,φk)=[1,ej2πd2sin φksin θk/λ,...,ej2πd2(M-1)sin φksin θk/λ]T。把N×M面阵分成M个子阵,子阵列2~M相当于子阵列1沿Y轴的偏移,相邻子阵列的方向矩阵之间相差一个固定值Ψ=diag(ej2πd2sin φ1sin θ1/λ,ej2πd2sin φ2sin θ2/λ,...,ej2πd2sin φKsin θK/λ),所以可得面阵的流型矩阵为 (4) 其中,Dm(·)表示由矩阵的m行构造的一个对角矩阵。因此,阵列的快拍矢量模型为[17] X(t)=AS(t)+N(t) (5) 其中,S(t)为信源的K×1维数据矢量,X(t)为NM×1维接收信号的数据矢量,N(t)为阵列的NM×1维高斯白噪声数据矢量。 跳频信号是宽带信号,每一跳的载频随机跳变,面阵的流型矩阵也随着载频跳变而跳变,但是在某一跳持续时间内,不管阵列接收到多少个跳频信号,每个跳频信号的载频都是恒定的,因此流型矩阵也是固定的,可以将其简化为窄带信号处理。针对跳频信号简化为窄带信号处理问题,已经有一些学者对其做了研究,得到跳频信号的清晰时频图是最为关键的步骤,因为时频图会直接影响有效hop的提取,进而影响DOA估计和网台分选的性能。文献[5]采用多相滤波器组的方法得到跳频信号的全景时频图,然后提取出跳频信号的有效hop,再根据有效hop进行DOA估计;文献[6]采用短时傅里叶变换(STFT)和平滑魏格纳分布(SPWVD)的组合时频方法提取出跳频信号有效hop;文献[7- 8]在文献[6]的基础上,对组合时频方法做出了不同的改进,抑制了交叉项,并结合时频单源点设置噪声门限,有效的去掉了噪声,得到了清晰稳健的时频图,提高了提取有效hop的性能。为了进一步提高DOA估计性能,本文采用形态学滤波的方法对跳频信号的时频图进行修正,完成有效hop的提取。 (6) f⊙P=min{W(x-x′,y-y′)- P(x′,y′)|(x′,y′)∈DP} (7) f⊕P=max{W(x-x′,y-y′)+ P(x′,y′)|(x′,y′)∈DP} (8) 其中,DP为P的定义域。 考虑到采用结构元素对图像进行处理时,只能提取与结构元素形状大小相同的结构,因此取结构元素P取为矩阵[1 1 1]。经过腐蚀和膨胀可以得到一个比较清晰的时频矩阵,再通过坐标变换将时频矩阵从二值图像转化为清晰稳健的时频图。图3和图4分别为经过SPWVD处理得到的时频图及形态学滤波修正后的时频图。对比图3和图4,用形态学滤波处理之后的时频图更加清晰。 图3 SPWVD变换后的信号时频图Fig.3 TF image after SPWVD 图4 形态学滤波处理后的时频图Fig.4 TF image after morphological processing 针对跳频信号任意一跳,采用酉ESPRIT算法进行2D-DOA估计,该算法将接收数据从复数域转化为实数域,然后特征值分解和矩阵运算都在实数域处理,大大降低了算法的计算复杂度,并根据相同的T矩阵,得到配对好的俯仰角和方位角信息。假设跳频信源个数为K,并且在任意时频点上信源个数小于阵元数。 采用酉ESPRIT算法第一步就要把复数域数据X矩阵转化为实数域矩阵。定义矩阵 (9) (10) 分别为偶次阶和奇次阶的酉变换矩阵,其中,Πn为反对称单位矩阵。构造酉变换矩阵QN和QM,将复数矩阵X转化为实数矩阵Y,即 (11) 定义选择矩阵 J1=[I(N-1)(N-1),0(N-1)×1] (12) J2=[0(N-1)×1,I(N-1)(N-1)] (13) (14) (15) (16) 同理,对于Y轴方向输出推导可得 (17) 考虑接收到K个跳频信号的情况,即 (18) (19) 由于是相同的T矩阵,可将其合并成一个新矩阵 (20) 对得到的P矩阵进行特征值分解(设特征值为λk) (21) 最后由μk和νk得到俯仰角和方位角估计值,即 (22) 基于以上分析,利用酉ESPRIT算法可以对多跳频信号的俯仰角和方位角进行联合估计。算法具体步骤如表1所示。 表1 本文算法步骤 续表1 (23) 在Step4中构造矩阵E以及求解信号子空间时,算法复杂度为 (24) O3≈4T(MN)2 (25) 表2 Step5的算法复杂度 在Step6中,主要计算公式(21)、(22)处理的矩阵维数都比较低,计算复杂度可以忽略不计。综上所述,可得酉ESPRIT算法的计算复杂度为 OU-ESPRIT=O1+O2+O3= (26) 根据文献[14]、[15]可知,对于面阵结构阵列,传统的最小二乘ESPRIT算法的计算复杂度为 OLS-ESPRIT=O(20(MN)3+10T(MN)2) (27) 对比公式(26)和公式(27)可知,一般情况下,由于采样点数T远大于MN, 因此,本文算法的复杂度可以减小到传统ESPRIT算法的0.65倍左右。 本节通过仿真实验对算法性能进行验证。假设空间中存在5个远场跳频信号FH1、FH2、FH3、FH4、FH5的俯仰角分别为θ1=15°、θ2=30°、θ3=45°θ4=60°、θ5=75°,方位角分别为φ1=80°、φ2=60°、φ3=40°、φ4=20°、φ5=10°,跳频周期为10 μs,载频归一化频率在0~0.7之间跳变。进行200次蒙特卡洛实验作为实验结果,将DOA估计的总体均方根误差和总体估计成功率作为衡量算法性能的标准。其中,总体均方根误差定义为[10] (28) ζ=P1/P (29) 其中,P1代表所有估计值偏差均小于1°成功的实验次数和。 实验1为了验证本文算法能够同时对多个跳频信号进行DOA估计,假设阵列结构为4×4均匀面阵,d1=d2=0.5 m,空间中存在5个跳频信号,采样点数为600,信噪比为5 dB,进行200次蒙特卡洛仿真。图5和图6分别为本文算法及ESPRIT算法估计得到的俯仰角和方位角散列图。 图5 本文算法散列图Fig.5 The hash map of algorithm of this paper 图6 ESPRIT算法散列图Fig.6 The hash map of ESPRIT algorithm 由图5和图6的仿真结果表明,本文算法和ESPRIT算法都可以实现5个跳频信号的DOA同时估计,但是本文算法得到的散列图比ESPRIT算法得到的散列图分布更集中,表明200次实验中得到的大多数估计值与真实值的差距更小,估计精度更高。此外,在用ESPRIT算法进行DOA估计时,需要考虑角度配对问题,跳频信号源越多,配对难度就越大,而本文算法则可以自动配对。 实验2为了验证信噪比对算法性能的影响,假设信噪比从-5 dB以1 dB为步进逐渐增加到20 dB,各信噪比下进行200次蒙特卡洛仿真,其他实验条件同实验1。图7和图8分别为总体均方误差曲线和总体估计成功率。 图7的实验结果表明,随着信噪比的增大,本文算法和ESPRIT算法DOA估计的总体均方根误差都逐渐减小;当信噪比小于10 dB时,本文算法的均方根误差明显小于ESPRIT算法;当信噪比大于10 dB时,本文算法的均方根误差与ESPRIT算法接近,并且逐渐趋于稳定。图8的实验结果表明,随着信噪比的增大,本文算法与ESPRIT算法DOA估计成功率都逐渐增大,本文算法估计成功率略大于ESPRIT算法;本文算法在信噪比为9 dB时,估计成功率达到100%,而ESPRIT算法需要达到12 dB左右。 图7 实验2的总体均方根误差Fig.7 The total RMSE of Experiment 2 图8 实验2的总体估计成功率Fig.8 The total success rate of Experiment 2 实验3为了验证快拍数据量对算法性能的影响,假设各跳快拍数从400逐渐增加到2000,信噪比分别取0 dB和6 dB时,其他实验条件同实验1。本文算法及ESPRIT算法DOA估计的总体均方根误差及总体估计成功率如图9和图10所示。 图9的实验结果表明,在不同信噪比下,随着快拍数据的增加,本文算法与ESPRIT算法总体均方根误差都逐渐减小,即跳频信号持续时间越长,采样获得的观测数据越多,估计性能越好。图10的实验结果表明,在不同信噪比下,两种算法的总体估计成功率都随着快拍数据增加而逐渐增加,各快拍数据下,本文算法估计成功率均优于ESPRIT算法。 图9 实验3的总体均方根误差Fig.9 The total RMSE of Experiment 3 图10 实验3的总体估计成功率Fig.10 The total success rate of Experiment 3 综合图9和图10的实验结果表明,快拍数据较大时,ESPRIT算法的估计性能与本文算法比较接近;快拍数据较小时,本文算法估计性能明显大于ESPRIT算法。 实验4为了验证阵元数量对算法性能的影响,假设信噪比从0 dB逐渐增加到20 dB,阵列结构均为均匀面阵,阵元数量为3×3、4×4、5×5,其他实验条件同实验1。图11和图12为算法性能与阵元数目的关系曲线。 从图11可见,在相同阵型下,随着信噪比递增,本文算法比传统ESPRIT算法始终表现出更好的估计性能,并且更适用于低信噪比的情况;在估计算法一致的情况下,阵元数越多,估计精度越高。图12的仿真结果表明,在相同阵型下,随着信噪比的增大,本文算法的总体估计成功率始终更高,低信噪比下两种算法差距更加明显。 图11 实验4的总体均方根误差Fig.11 The total RMSE of Experiment 4 图12 实验4的总体估计成功率Fig.12 The total success rate of Experiment 4 实验5为了验证本文算法相比较ESPRIT算法在算法复杂度上的优势。假设空间存在5个跳频信号,信噪比为5 dB,各跳快拍数据为3000,接收阵列结构分别为3×3、4×4、5×5、6×6、7×7、8×8时两种算法DOA估计所需时间(单位:s)如表3所示。 表3 两种算法2D-DOA估计所需时间比较 由表3可见,随着阵列数量的增加,本文算法与ESPRIT算法计算耗时都逐渐增加,但是ESPRIT算法的耗时增加更显著;在阵列数量相同时,本文算法计算耗时均小于ESPRIT算法,并且本文算法的耗时大于为ESPRIT算法耗时的0.6~0.75倍。 综上仿真实验表明,本文算法的估计精度会随着快拍数、信噪比、阵列元数的增加而逐渐提升;在低信噪比、低快拍数据、阵列元数较少的情况下,本文算法的性能会变差,但是与传统的ESPRIT算法相比,本文算法的估计性能仍然更优,体现了本文算法具有更强的适用性和更好的估计性能。 跳频信号的空域信息可以有效辅助跳频信号网台分选,为了获得精确的2D-DOA信息,本文首先建立跳频信号的平面阵列快拍数据模型;然后用形态学滤波的方法对时频图进行修正,提取出跳频信号的有效hop,针对某一跳,把它当作一个窄带信号处理;最后采用酉ESPRIT算法实现跳频信号2D-DOA联合估计。与传统ESPRIT算法相比,酉ESPRIT算法将复数域的特征值分解和矩阵运算转化到实数域处理,使得计算复杂度大大降低;构造实数矩阵时,重复利用了接收数据,提高了估计精度,且可实现参数自动配对。仿真结果验证了本文算法能够更为精确地估计2D-DOA,具有更高的适用性,有一定的工程实用价值。 [1] Sha Z C, Liu Z M, Huang Z T, et al. Online Hop Timing Detection and Frequency Estimation of Multiple FH Signals[J]. ETRI Journal, 2013, 35(5):748-756. [2] Belouchrani A, Amin M G. Time-frequency MUSIC[J]. IEEE Signal Processing Letters, 2002, 6(5):109-110. [3] Belouchrani A, Amin M G. Blind source separation based on time-frequency signal representations[J]. IEEE Transactions on Signal Processing, 1998, 46(11):2888-2897. [4] Li Q, Liu Y, Chen H. Direction of arrival estimation using array model in time-frequency domain[J] International Conference on Audio Language and Image Processing. IEEE, 2010:1112-1116. [5] 陈利虎,张尔扬.基于数字信道化和空时频分析的多网台跳频信号DOA估计[J].通信学报,2009,30(10):68-74. Chen L H, Zhang E Y. Directions of arrival estimation for multi frequency-hopping signals based on digital channelized receiver and spatial time-frequency analysis[J]. Journal on Communications, 2009, 30(10):68-74. (in Chinese) [6] 陈利虎,王永明,张尔扬.基于空时频分析的多FH/DS信号DOA估计[J].信号处理,2009,25(8):1309-1313. Chen L H, Wang Y M, Zhang E Y. Directions of arrival estimation for multicomponent frequency-hopping direction sequence spread spectrum signals based on spatial time-frequency analysis[J]. Signal Processing, 2009, 25(8):1309-1313.(in Chinese) [7] 张东伟, 郭英, 齐子森,等. 多跳频信号2D-DOA与极化参数的联合估计[J]. 华中科技大学学报:自然科学版, 2015(9):84- 88. Zhang D W, Guo Y, Qi Z S, et al. A joint estimation of 2D-DOA and polarization estimation for multiple frequency hopping signals[J]. Journal of Huazhong University of Science & Technology,2015(9):84- 88. (in Chinese) [8] 张东伟, 郭英, 齐子森,等. 跳频信号2D-DOA与极化参数的欠定估计[J]. 哈尔滨工业大学学报, 2016, 48(4):121-128. Zhang D W, Guo Y, Qi Z S, et al. Underdetermined estimation of 2D-DOA and polarization for frequency hopping signals[J]. Journal of Harbin Institute of Technology, 2016,48(4):121-128. (in Chinese) [9] 于欣永, 郭英, 张坤峰,等. 基于STFD & SCMUSIC的多跳频信号DOA估计与网台分选[J].信号处理, 2017,33(10):1344-1351. Yu X Y, Guo Y, Zhang K F, et al. DOA Estimation and Network Sorting Based on STFD & SCMUSIC of Multi-FH Signal[J]. Journal of Signal Processing, 2017,33(10):1344-1351. (in Chinese) [10] 程标, 于宏毅, 胡赟鹏,等. 随机布局天线系统的跳频信号分选研究[J]. 信号处理, 2015,31(8):1020-1028. Chen B, Yu H Y, Hu Y P, et al. The Study of Frequency-Hopping Networks Sorting Based on Randomly Distributed Antenna System[J]. Journal of Signal Processing, 2015,31(8):1020-1028. (in Chinese) [11] Almidfa K, Tsoulos G V, Nix A. Performance analysis of ESPRIT, TLS-ESPRIT and Unitary-ESPRIT algorithms for DOA estimation in a W-CDMA mobile system[J]. 3G Mobile Communication Technologies, 2000. First International Conference on. IET, 2000:200-203. [12] Zheng G M, Chen B X, Yang M L. Unitary ESPRIT algorithm for bistatic MIMO radar[J]. Electronics Letters, 2012, 48(3):179-181. [13] Wang X, Zhang M, Zhao J. Efficient Cross-Range Scaling Method via Two-Dimensional Unitary ESPRIT Scattering Center Extraction Algorithm[J]. IEEE Geoscience & Remote Sensing Letters, 2015, 12(5):928-932. [14] Zhou Y, Fei Z, Yang S, et al. Joint Angle Estimation and Signal Reconstruction for Coherently Distributed Sources in Massive MIMO Systems Based on 2D Unitary ESPRIT[J]. IEEE Access, 2017, PP(99):1-1. [15] Zheng G, Tang J, Yang X. ESPRIT and Unitary ESPRIT Algorithms for Coexistence of Circular and Noncircular Signals in Bistatic MIMO Radar[J]. IEEE Access, 2017, 4(99):7232-7240. [16] 刘帅琦, 王布宏, 李龙军,等. 二维混合MIMO相控阵雷达的DOA估计算法[J]. 西安电子科技大学学报:自然科学版, 2017,44(3):157-163. Liu S Q, Wang B H, Li L J, et al. DOA estimation method for two-dimensional hybrid MIMO phased-array radar[J]. Journal of Xi’an University of Electronic Science and Technology: Natural Science Edition, 2017, 44(3):157-163. (in Chinese) [17] 闫金山,彭秀艳,王咸鹏. 基于Unitary ESPRIT的双基地MIMO雷达目标定位算法[J]. 哈尔滨工程大学学报,2012(3):342-346. Yan J S, Peng X Y, Wang X P. Target localization for MIMO radar based on Unitary ESPRIT[J]. Journal of Harbin Engineering University, 2012(3):342-346. (in Chinese) [18] 杨银松,郭英,于欣永,等.基于酉ESPRIT的跳频信号DOA估计[J]空军工程大学学报:自然科学版,2018,19(2):60- 67. Yang Y S, Guo Y, Yu X Y, et al. DOA Estimation of Frequency Hopping Signal Based on Unitary ESPRIT[J]. Journal of Air Force Engineering University: Natural Science Edition, 2018,19(2):60- 67. (in Chinese) [19] 张小飞,陈华伟,仇小峰,等.阵列信号处理及MATLAB实现[M].北京:电子工业出版社,2015.1. Zhang X F, Chen H W, Chou X F, et al. Array signal processing & MATLAB[M]. Beijing: Electronic Industry Press, 2015.1. (in Chinese) [20] 宫翔, 王振华, 王晨光. 基于时频分析与形态学滤波的跳频参数估计[J]. 空军预警学院学报, 2011, 25(4):243-246. Gong X, Wang Z H, Wang C G. Parameter estimation of frequency hopping signal based on time-frequency analysis and morphological filtering[J]. Journal of Air Force Radar Academy, 2011, 25(4):243-246. (in Chinese)
3 跳频信号有效跳的提取
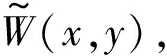
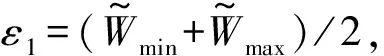

4 基于酉ESPRIT算法的跳频信号2D-DOA估计算法步骤

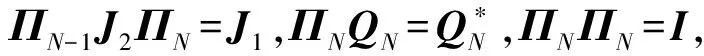
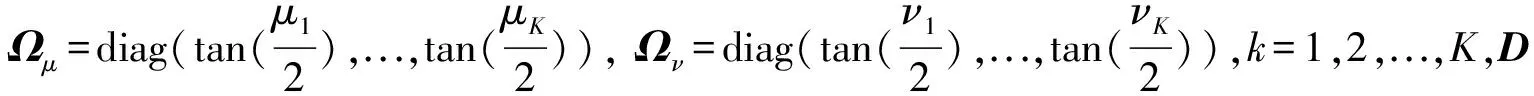




5 算法复杂度分析
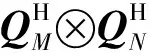

6 仿真与分析




7 结论
