设置横系梁的双柱式桥墩地震易损性分析

陈静恭， 张于晔， 耿 波

(1. 南京理工大学 理学院， 江苏 南京 210094； 2. 招商局重庆交通科研设计院有限公司， 重庆 400067)

桥墩作为桥梁结构中重要的承重和抗侧力构件，其在地震作用下较易发生破坏，从而影响整个桥梁结构的抗震安全性[1,2]。当双柱式桥墩高度较高时，为保证桥墩的整体性和抗侧移能力，通常需在双柱墩间设置横系梁。一般而言，横系梁设置会对双柱式桥墩的抗震性能有较大影响，但对其抗震性能影响程度的定量评估一直是难点问题[3,4]。

为定量分析桥墩在不同强度地震作用下的破坏概率水平，可基于易损性方法进行计算评估。地震易损性分析指桥梁结构在不同水平地震作用下超越某一极限状态或性能水平的概率。易损性曲线分为经验易损性曲线和理论易损性曲线。Shinozuka等[5]利用实际工程中桥梁地震破坏的数据得到经验易损性曲线。Hwang等[6,7]提出了桥墩理论易损性曲线方法。由于横系梁的存在，导致双柱式桥墩在横向地震作用下墩顶位移能力的不确定性，顺桥向计算墩顶位移能力方法无法适用于横桥向墩顶位移能力的计算，墩顶弹塑性位移能力比顺桥向时更加复杂，国内外研究大多针对桥梁在顺桥向地震波作用下桥梁结构或构件的易损性。因此，对于在横向地震波作用下双柱式桥墩的易损性分析，还需进行深入研究。

鉴于此，本文基于易损性方法研究横向地震作用下横系梁设置对桥墩抗震性能的影响。首先，基于Pushover分析和位移破坏准则，得到双柱式桥墩在横桥向地震作用下墩顶的位移，在此基础上提出计算其墩顶位移能力的经验公式。然后，建立典型梁桥非线性分析模型，并改变横系梁刚度、高度、根数等设计参量，研究其对双柱式桥墩地震易损性的影响。最后，通过非线性时程分析得到桥墩位移响应，并与其位移能力进行对比，从而获得双柱式桥墩在横向地震作用下的易损性曲线。

1 易损性分析方法介绍

1.1 易损性曲线

结构地震易损性分析是指在可能遭受的各种强度地震作用下，结构发生某种程度破坏的概率，可用式(1)来表示。

(1)

式中：Pf为失效概率；Dd为地震需求；Dc为结构抗力；IM为地震动参数。

为了得到易损性曲线，需要得到结构的需求和能力。Gardoni[8]通过贝叶斯方法建立了概率地震需求模型(Probabilistic Seismic Demand Model，PSDM)。PSDM建立了结构需求Dd和地震动参数IM之间的关系。本文通过建立双柱式桥梁的概率地震需求模型进行非线性时程分析，选取桥墩位移延性比μd为结构需求指标，以地面峰值加速度PGA作为地震动参数。

1.2 形成双柱式桥墩易损性曲线主要步骤

横系梁的设置会使双柱式桥墩受横向地震作用时的损伤机制发生改变，从而使得桥墩在顺桥向的位移能力和横桥向的位移能力完全不同。针对这一特点，本文基于可靠度概率分析的理论分析方法，形成双柱式桥墩在不同横向地震作用下对应不同破坏状态的易损性曲线，主要步骤如下：

(1)利用OpenSees建立合理的桥梁有限元模型；

(2)从太平洋地震工程研究中心选取56条合适的地震波，形成一系列“桥梁-地震动”样本；

(3)基于位移破坏准则，利用Pushover找到桥墩在不同破坏状态时墩顶的位移，确定桥墩在不同破坏状态下的位移能力，形成桥墩在横向地震作用下对应于不同破坏状态时的损伤指标，并且提出计算桥墩墩顶横向位移能力的经验公式；

(4)对步骤(1)中桥梁有限元模型进行非线性时程分析，得到桥墩的响应；

(5)得到结构在不同等级地震动作用下超过某一破坏状态的概率函数，最终形成双柱式桥墩易损性曲线。

2 双柱式桥墩分析实例

2.1 模型构建

以某4跨混凝土连续梁桥为例，跨径布置4×30 m，墩高为30 m，主梁采用C50混凝土，桥墩和横系梁用C40混凝土，墩柱为2.1 m×2.1 m的实心方形混凝土柱，纵筋和箍筋都采用HRB335，纵向配筋率为0.852%，配箍率0.485%。支座GJZ为550 mm×600 mm×130 mm，橡胶层厚度t=95 mm，最大承载力为3186 kN，地质条件是Ⅱ类场地。桥梁结构布置和分析模型如图1所示。

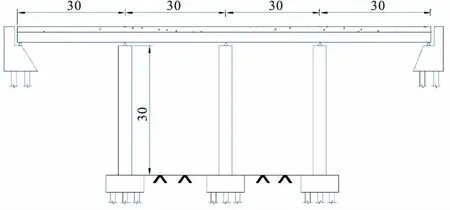
图1 桥梁结构示意/m

在地震作用下，桥梁上部结构通常不会进入塑性范围，因此本桥模型主梁采用弹性梁单元模拟。墩柱在强烈地震动作用时下部会形成塑性铰区域，横系梁和墩柱均使用弹塑性梁柱单元进行模拟。桥墩与上部结构之间利用板式橡胶支座连接，支座采用零长度单元模拟，桥墩墩底采用固接形式。

2.2 不同墩柱工况

为了研究横系梁对双柱式桥墩在横向地震作用下易损性的影响，改变横系梁根数(1～2根)、高度(0.3H，0.5H，0.7H，H为墩柱高度)、横系梁与墩柱刚度比(0.15，0.34，0.54，1)，形成八种不同工况。工况示意图如图2所示。详细不同参数变化情况列于表1。

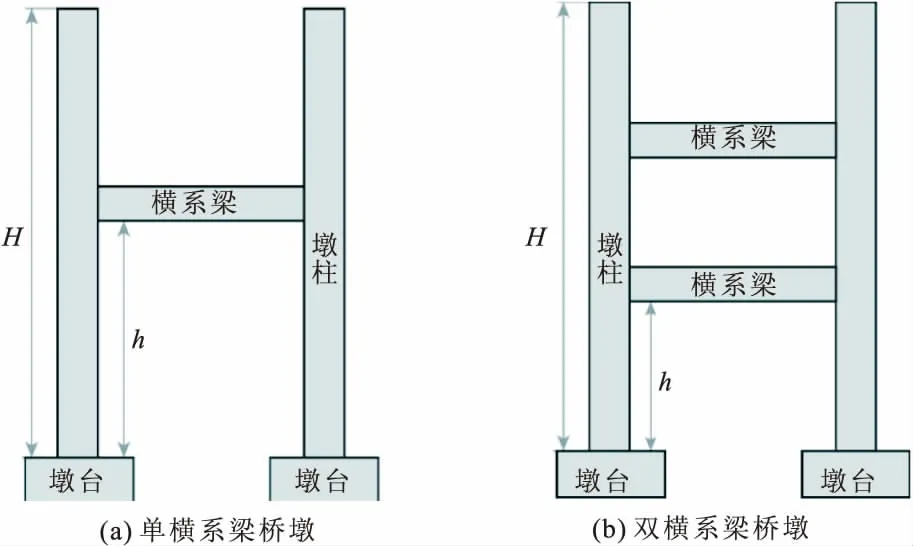
图2 双柱墩结构示意

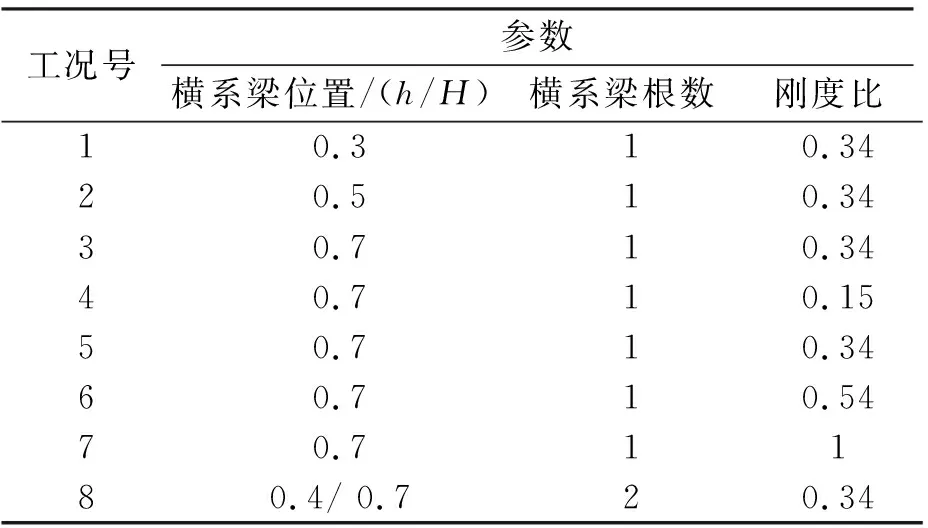
表1 桥墩工况参数变化

2.3 地震动输入

本文根据实际桥梁的场地类型选用地震波，从美国太平洋地震工程研究中心强震数据库中选取。从强震数据库中选取了56条地震记录，震波选取的时候尽量广泛。56条地震波的PGA分布如图3 所示，PGA范围0～0.8g。

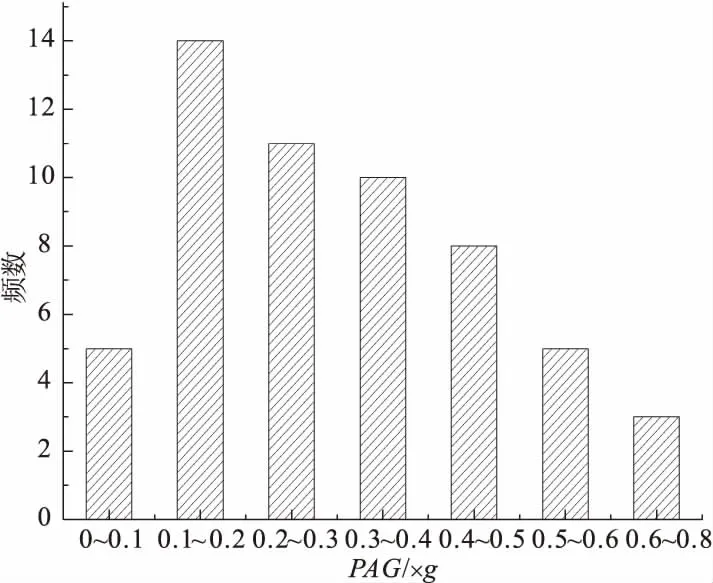
图3 56条地震波PGA频数分布

3 损伤指标确定

要评价桥梁结构的易损性，首先要根据性能水准来确定结构的破坏状态并量化其损伤指标。Berry等[9]选取混凝土开裂和钢筋弯曲作为破坏状态。Hwang等[10]选取桥墩延性需求作为判定标准。基于位移的抗震设计方法强调以位移作为控制设计的主要参数。基于位移破坏准则，本文通过Pushover找出了几种破坏状态所对应的位移，确定横桥向方向的损伤指标。

Hwang采用相对位移延性比来对桥梁的破坏状态进行定义，研究分析不同破坏状态下对应的桥梁性能。并根据HAZUS99[11]中的定义，将桥梁的五种破坏状态表述为：无破坏、轻微破坏、中等破坏、严重破坏和完全破坏，如下表2所示。μd是柱顶相对位移最大值Δ与初始屈服位移Δcy1)的比值。

(2)

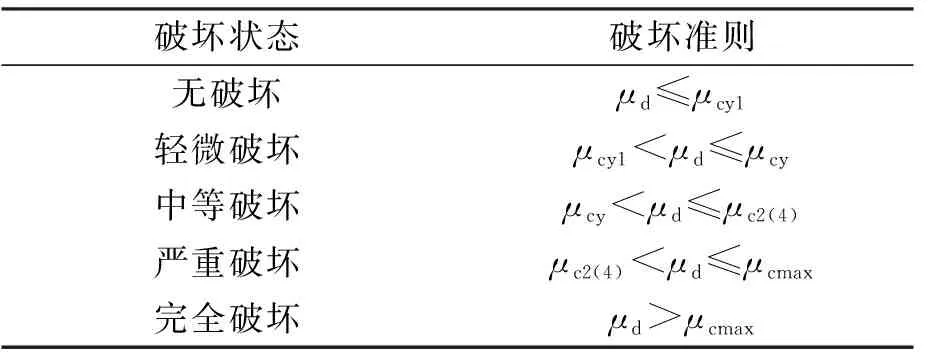
表2 桥墩相对位移延性比所对应的破坏状态

注：表中μcy为屈服位移延性比；μc2(4)为柱截面边缘钢筋混凝土压应变达到0.002或0.004 时的位移延性比；μcmax为最大位移延性比，μcmax=μc4+3

由于桥墩横系梁的设置，上述方法不完全适用于分析有横系梁的双柱式桥墩。考虑横系梁的作用，利用OpenSees建立30个桥墩模型，改变其横系梁高度，高度的变化从0.2H～0.7H等距增加，对其进行Pushover分析。分别找到桥墩钢筋首次屈服和柱截面边缘混凝土压应变达到0.004时桥墩的墩顶位移。基于计算单柱墩弹塑性位移能力公式，引入一个与横系梁高度h相关的系数对单柱墩位移公式进行调整，使其适用于双柱墩弹塑性位移能力计算。

在OpenSees桥墩模型中，墩柱和横系梁使用弹塑性梁柱单元模拟，墩顶轴力为5600 kN，模拟桥墩上部荷载作用，墩底固接。桥墩的Pushover部分分析结果如表3所示。

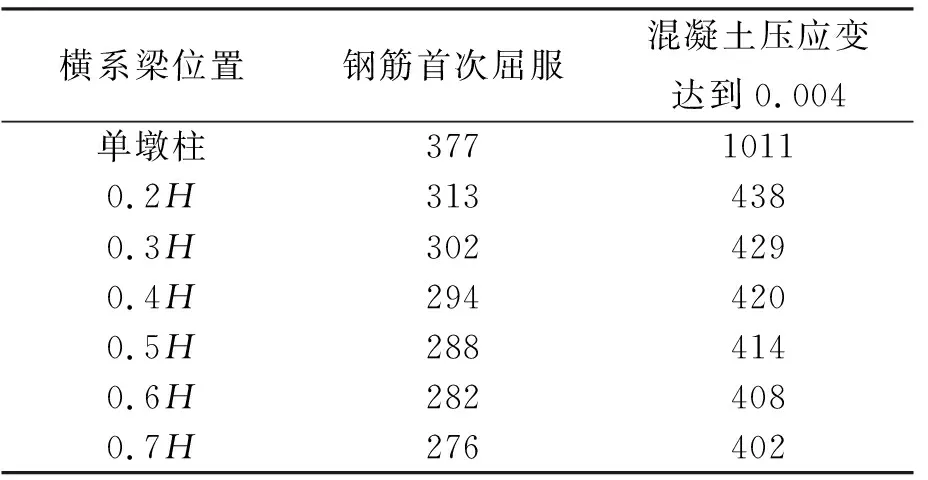
表3 Pushover分析得到的部分墩顶位移mm

将所有Pushover分析结果，以横系梁高度为横坐标，墩顶位移为纵坐标进行拟合分析。其结果如图4所示。

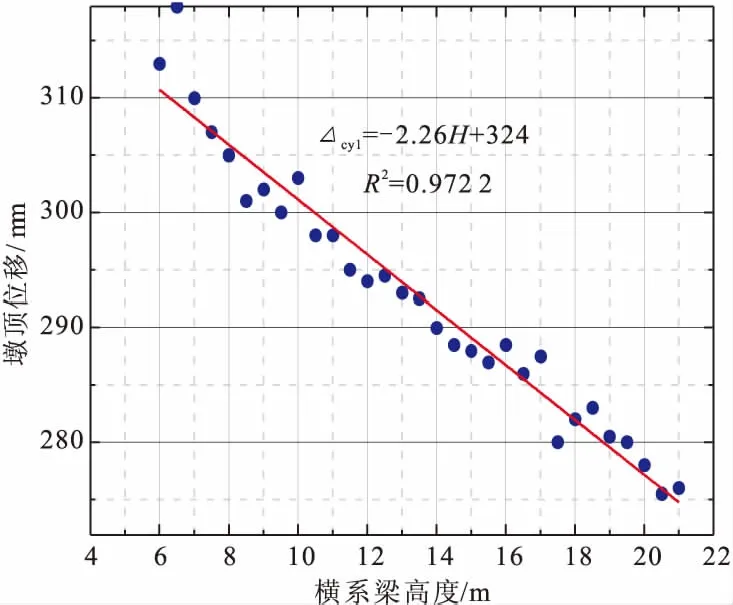
图4 桥墩位移回归分析

根据文献[12]规范可知，单柱墩计算其墩顶屈服位移公式为：

(3)

式中：φy′为截面屈服曲率。

将图4中的拟合公式提出计算单柱墩墩顶屈服位移公式部分，则公式(3)变换为：

(4)

确定合理的塑性铰长度是精确计算墩顶塑性位移能力的关键。由Priestley等[13]提出的塑性铰长度计算经验公式被广泛认同，其公式为：

Lp=0.08H+0.022fyds≥0.04fyds

(5)

式中：Lp为塑性铰长度；fy为纵向钢筋强度代表值；ds为纵筋直径。

根据文献[12]，塑性转角计算公式为：

(6)

式中：θu为塑性转角；φu为截面极限破坏状态曲率；φy为等效屈服曲率；k安全延性系数(一般取值为2)。

最终得出双柱墩墩顶横向极限位移能力公式为：

(7)

通过Pushover分析发现，双横系梁在横向地震作用下位移和单横系梁在0.5H处位移能力相近。因此，双横系梁墩顶位移能力的计算可以此替代。

4 结构能力与响应概率分析

4.1 结构能力概率分析

在结构易损性分析中，地震作用下的结构需求概率分布μc可以用对数正态分布函数表示[14]：

(8)

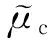
利用所拟合出的公式可求出桥墩不同破坏状态承载力均值。设置横系梁的双柱墩相对于单墩柱，初始屈服时的位移延性比相差不大，但最大延性比双柱墩明显低于单墩柱。详细数据如表4所示。

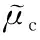
表4 不同破坏状态承载力均值

4.2 结构响应概率分析

结构响应同样可用对数正态分布函数来表示。

(9)

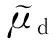
基于非线性时程分析，可得到桥墩在不同地震强度作用下的响应，将桥墩的响应值与地震动峰值加速度进行对数回归分析，如图5所示(工况5)。所有桥墩概率地震响应的概率需求模型，如表5所示(工况1～8)。

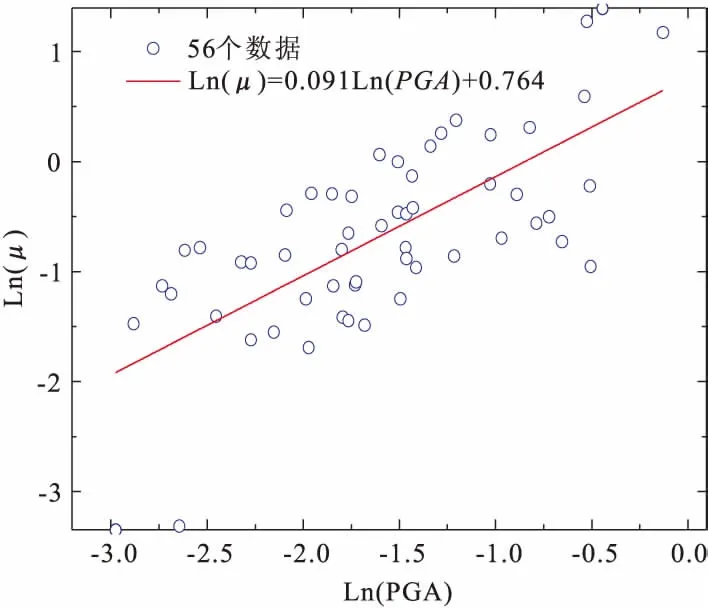
图5 桥墩需求响应值和峰值加速度对数回归分析

表5 桥墩概率地震响应的概率需求模型

注：表中μd1～μd8依次为八种工况的位移延性比；R2为结构地震需求样本方差

4.3 桥墩易损性曲线

桥墩需求μd超越桥墩能力μc的概率可用式(10)表示：

(10)

式中：由于μd，μc都服从标准正态分布，式(10)可变形为如下标准正态函数：

(11)

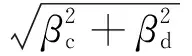
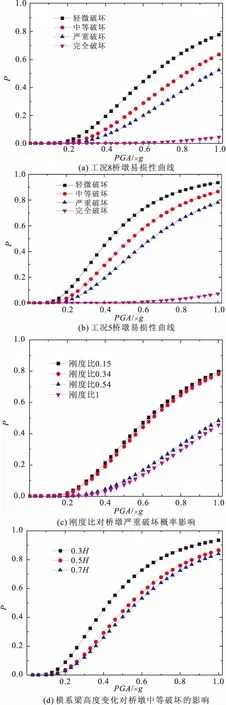
图6 双柱式桥墩不同工况下易损性曲线

图6a为设置双横系梁的双柱式桥墩(工况8)的易损性曲线，图6b为设置单横系梁且横系梁高度为0.7H的桥墩易损性曲线。通过对比图6a，6b可知，对于相同的破坏状态，设置双横系梁的桥墩破坏概率均比单横系梁桥墩低10%以上。这体现出设置双横系梁在抗震方面的优势。

为分析横系梁与墩柱的不同刚度比对桥墩易损性曲线的影响，将严重破坏阶段易损性曲线列于图6c进行对比。当PGA为0.8g时，刚度比为0.15，0.34，0.54，1时的破坏概率分别为66.8%，64.6%，32.8%，29.4%，随着刚度比的增加，桥墩的破坏概率逐渐减小。刚度比0.15相较于刚度比为1，前者破坏概率增加超过30%。当刚度比大于0.54时，破坏概率减小的幅度大幅降低。

图6d为横系梁高度分别为0.3H，0.5H，0.7H时桥墩中等破坏的易损性曲线。曲线表明，在PGA为0.6g的地震动作用下，当横系梁高度为0.3H时，桥墩破坏概率为72.7%，当横系梁高度为0.5H时，桥墩破坏概率为57.3%，而当横系梁高度为0.7H时，桥墩破坏概率降低到53.2%，横系梁位置的高度对桥墩横向破坏影响显著。

5 结 论

本文针对设置横系梁的双柱式桥墩的横向位移能力计算复杂的特点，对大量双柱式墩桥有限元模型进行Pushover分析，提出了计算双柱式桥墩在受横向地震作用下对应不同破坏状态墩顶位移能力的经验公式。通过典型桥梁的分析，研究了横系梁刚度、高度、根数等参数对双柱式桥墩易损性的影响，得到以下结论：

(1)相对于设置单横系梁的双柱式桥墩，设置双横系梁的双柱式桥墩的破坏概率可降低10%以上。同等地震作用下，后者具更好的抗震安全性。

(2)横系梁与墩柱的刚度比对桥墩的破坏概率影响显著。当刚度比在0.15～1之间时，刚度比的增大能够明显降低墩柱的破坏概率，相对于刚度比为0.15，刚度比为1时的破坏概率会低30%以上，刚度比设置在0.5～1之间比较合适。

(3)在横桥向地震输入下，横系梁的位置高度对桥墩的破坏概率有一定的影响。当横系梁位置在0.3H～0.7H之间时，桥墩的破坏概率会随着横系梁高度的减小而增加。