三维无线电能传输线圈磁场的仿真分析
2018-08-18余成波
余成波 张 林 曾 亮
三维无线电能传输线圈磁场的仿真分析
余成波 张 林 曾 亮
(重庆理工大学,重庆 404000)
感应线圈作为一种无线电能发射装置,其产生的磁感应强度是影响其电能传输效率的重要因素之一。本文利用ANSYS建立了感应线圈的3D有限元模型,采用棱边单元法对发射线圈进行了求解分析,给出了发射线圈磁场强度的分布情况。通过改变线圈直径、线圈匝数、线圈匝间距的不同设计参数,分析研究影响磁场强度的因素以及改变这些关键因素来增强磁场强度,分析结果为优化感应线圈提供了理论依据。
发射线圈;有限元;磁场强度
传统电缆具有线路老化,尖端放电以及因为接触产生电火花等安全问题。无线电能传输没有导线连接,将电源侧电能安全的传输到用电侧,具有灵活、安全、低维护等优良特性[1-2]。但由于其松耦合的结构特点,传输效率较低,而影响系统传输效率的其中一个重要因素就是发射线圈产生的磁感应强度大小[3]。因此,研究线圈不同结构参数对磁感应强度的影响,具有重大的研究意义。
感应线圈的设计参数主要为:线圈总高度、线圈直径、线圈匝数、线圈匝间距、截面形状。感应线圈可以采用多种不同设计。目前国内外对线圈结构研究文献较少,主要集中在以下几个方面:①增加线圈的个数,如在装置中增加中继线圈[4];②设计不同截面形状的线圈,如MIT研究小组WPT系统采用稀疏圆形截面线圈作为发射线圈[5],法国AREVA公司的冷坩埚装置采用多匝密绕型矩形截面线圈作为发射线圈[6];③采用不同的绕制方式,如盘式谐振器和双层嵌套线圈[7];④设计发射和接受线圈的不同的放置位置,如共轴平行放置的Helmholtz线圈能满足较大范围的磁通量穿过[8]。以上方法虽然在一定程度上提高了系统的传输效率,但复杂的物理结构,给谐振频率的设计带来了一定的困难。利用ANSYS建模发射线圈,避免了复杂的物理结构设计。通过改变线圈自身参数进行磁场仿真计算,可以快速得到磁感应强度云图,大大地减少了工作量,简化了系统发射结构物理模型,为优化感应线圈提供了理论依据。
1 ANSYS电磁场基本理论
电磁场理论由一套麦克斯韦(Maxwell)方程组描述,由4个定律组成,分别是安培环路定律、法拉第电磁感应定律、高斯电通和高斯磁通定律。其微分形式如式(1)至式(4)所示,以其为基础可以导出有限元处理电磁问题的微分方程。
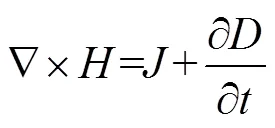
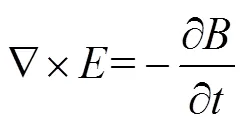
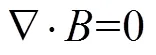
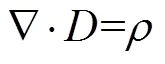
式中,为自由电荷体密度;为传导电流密度;/为位移电流密度。在介质内,上述麦克斯韦方程组尚不完备,需补充三个描述介质性质的方程,对于各同性线性介质式如(5)至式(7)所示。
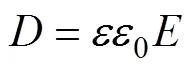

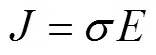
式中,、和分别为(相对)介电常量、磁导率和电导率。Maxwell式(1)至式(4)加上描述介质性质式(5)至式(7),全面总结了电磁场的规律,是电动力学的基本方程组,利用他们原则上可以解决各种电磁场问题[9]。
2 ANSYS仿真
本文建立的模型为载流绞线圈,空气不均匀地分布在线圈间距和空心范围内,故采用单元类型为SOLID236的单元棱边法进行3D建模。SOLID236是一个能够对电磁场进行建模的具有20个节点的3D单元,该单元具有电和磁的自由度,磁自由度基于边缘通量公式。
2.1 发射线圈模型的建立
以平面为圆平面,轴为高度建立线圈圆环模型,空气模型为砖形,如图1所示。通过布尔操作中的over运算将空气介质与线圈浇筑在一起。材料属性和模型参数设置见表1。

图1 线圈模型和砖型空气模型

表1 材料属性和参数设置
对所做的仿真,本文假设和约定如下:
1)近似认为材料各向同性。
2)不考虑温度变化的影响。
3)近似认为空气区域无限远。
2.2 模型的网格划分
网格划分对有限元的求解及其重要,单元越小,网格越细,则离散域的近似度越好,计算结果也越精确,但计算量及误差都将增大。本文建立的线圈模型是一个规则的柱体,采用体扫掠方式划分网格。空气模型经过浇筑之后形状变得复杂,采用自由方式划分网格。图2为线圈和空气的有限元模型,最后通过numcmp命令将其浇筑在一起。
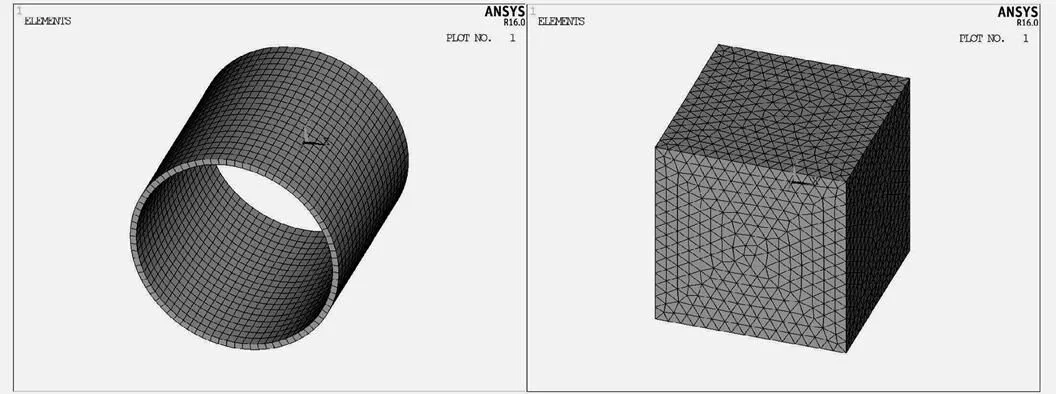
图2 线圈和空气网格划分图
2.3 施加载荷和边界条件
线圈作为载流块导体,模型是柱形,所以加载电流时需加载环形电流。切换当前坐标系为柱坐标系,将环形电流加载在有限元单元上,电流方向水平向右。线圈单元采用电磁场分析操作选项,源电流密度可以直接加在有限元单元上,如图3所示。
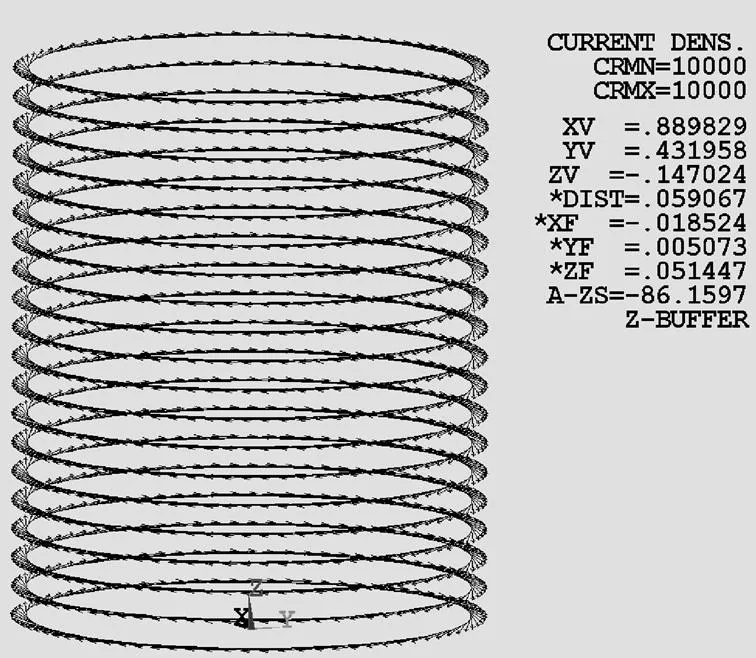
图3 环形电流模型
2.4 求解
对模型施加幅值为10kA的恒定电流,图4给出了线圈的加载情况。加载完毕后,选择波前求解器进行求解。
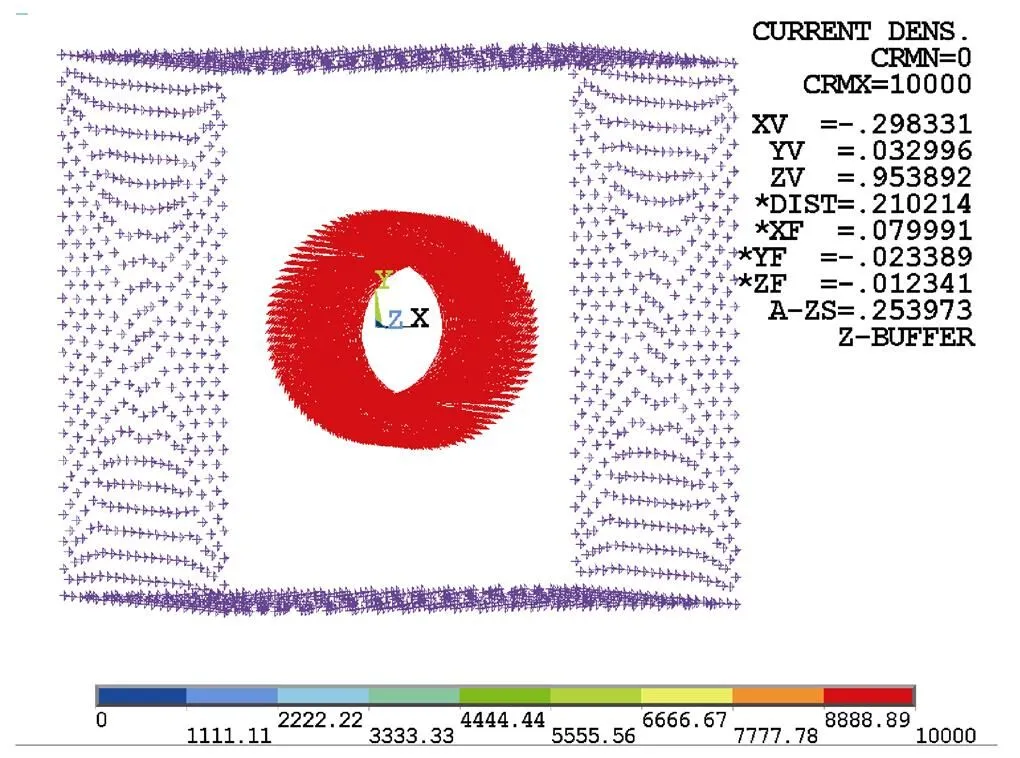
图4 施加载荷和边界件的模型
3 发射线圈磁场分布规律
采用波前求解器求解,在后处理器中查看求解结果。图5至图7给出了线圈在不同轴向分量上的磁场的分布情况。
图5为磁场强度()和磁感应通量()在轴方向上的磁场,由图可知,磁场强度与磁感应通量云图的分布规律一致。其原因为对于各同性线性介质来说,由式(5)可知,磁场强度与磁感应通量成线性关系,因此云图的分布规律一致,数值上为相对磁导率的倍数,理论与实验结果一致。
由图5至图7可知:不同颜色区域在轴中心处大致呈圆形沿平面向外扩大,并且每种颜色都在一定的圆形或环形柱体内。磁通量密度和磁场强度在平面内,沿着内径按梯度增大,并且在距离轴中心一定范围内有最大值。电流加载方向水平向右,磁力线方向在线圈内部竖直向上,外部磁力线向下,符合右手螺旋定则。同时,磁通密度矢量箭头在线圈两端分布为浅蓝色,磁通密度相对较弱。线圈中间分布呈橙红色,磁通密度大,线圈外部磁通密度急剧降低。越靠近感应线圈中心,磁力线分布越密集,磁通量密度越大。反之,则相反。发射线圈周围磁场分布规律符合其理论分布特性。
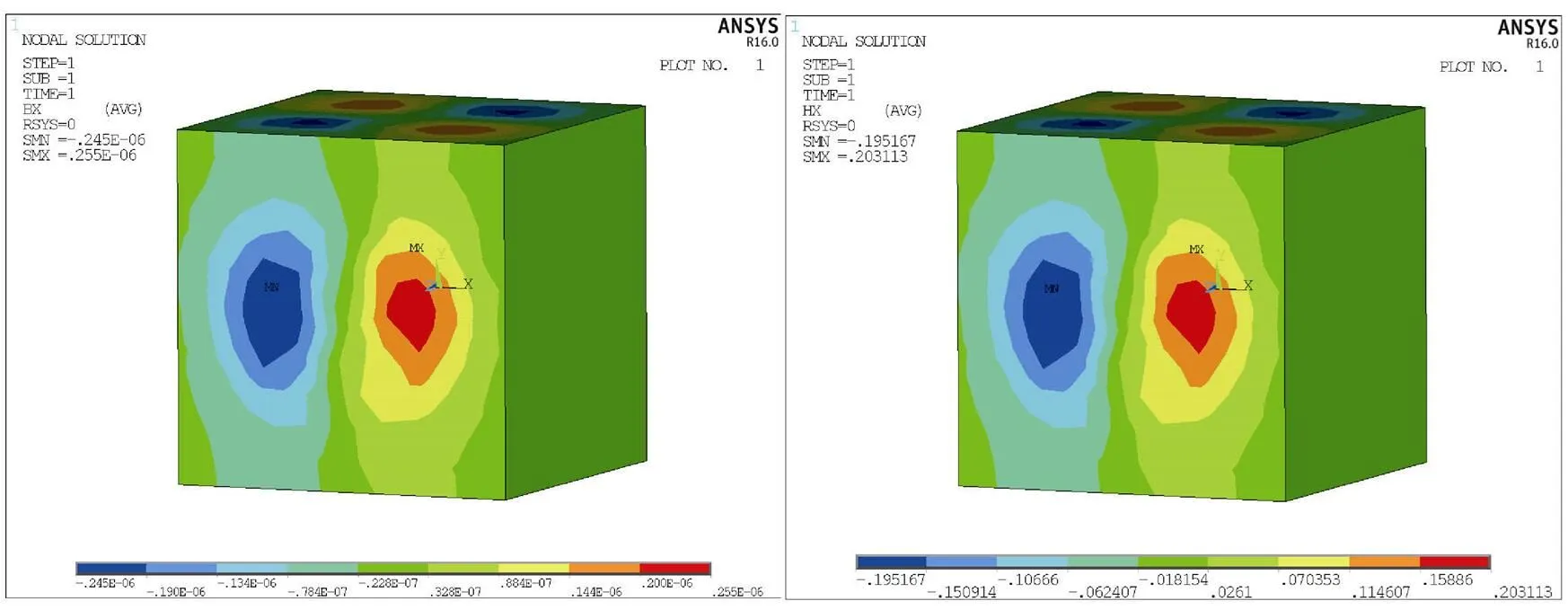
图5 X轴方向上H和B的分布云图

图6 Y轴方向上H和B的分布云图
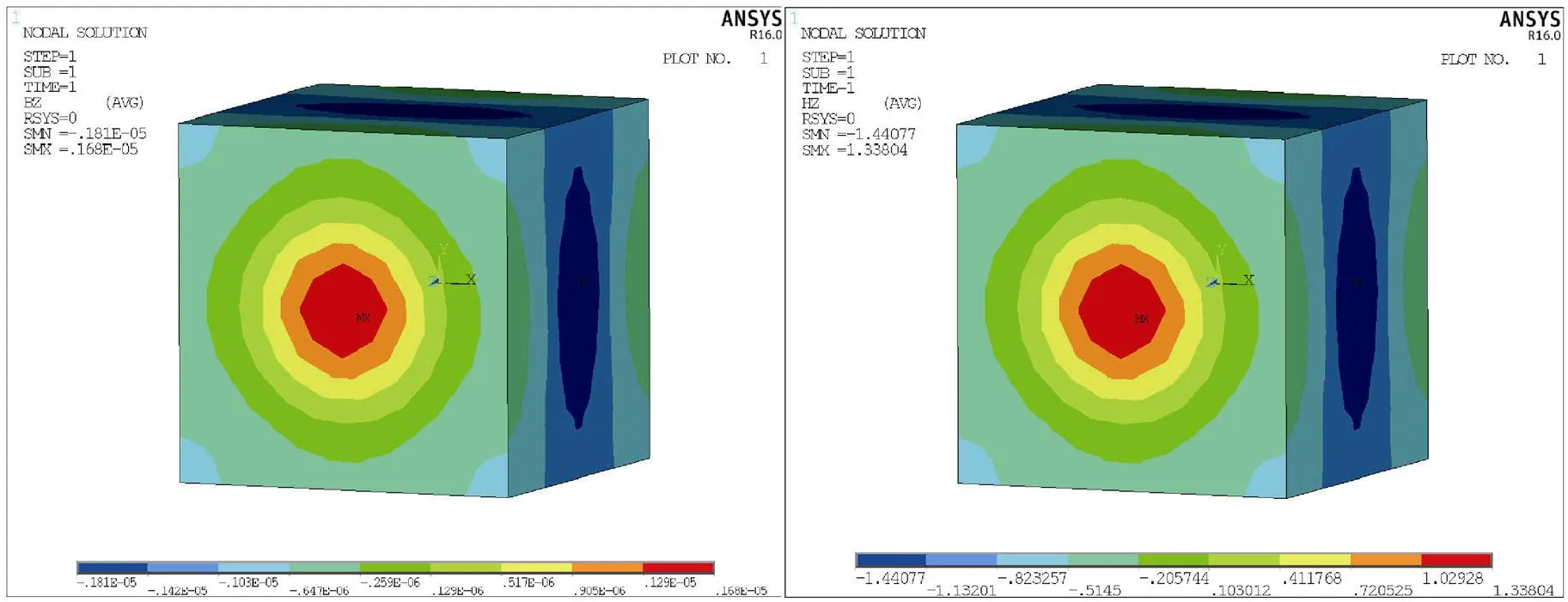
图7 Z轴方向上H和B的分布云图
4 线圈的结构因素对磁场强度的影响
本文采取控制变量的方法验证不同的线圈设计参数对线圈产生磁场强度的影响。从磁场强度云图中提取不同位置的磁场强度数据,绘制磁场强度曲线,分析不同参数下同一坐标位置下的磁场强度,得出结论。通入线圈电流幅值为10kA,发射线圈的结构参数见表2。
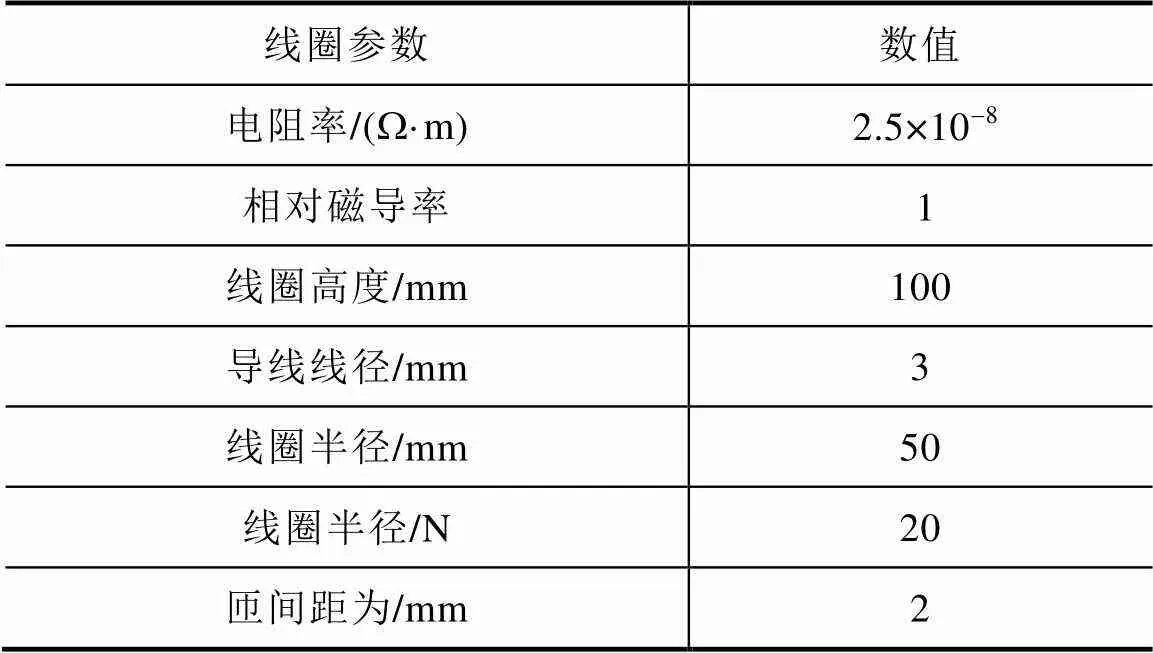
表2 发射线圈的结构参数
4.1 线圈半径对磁场强度的影响
设置线圈不同半径大小,见表3。
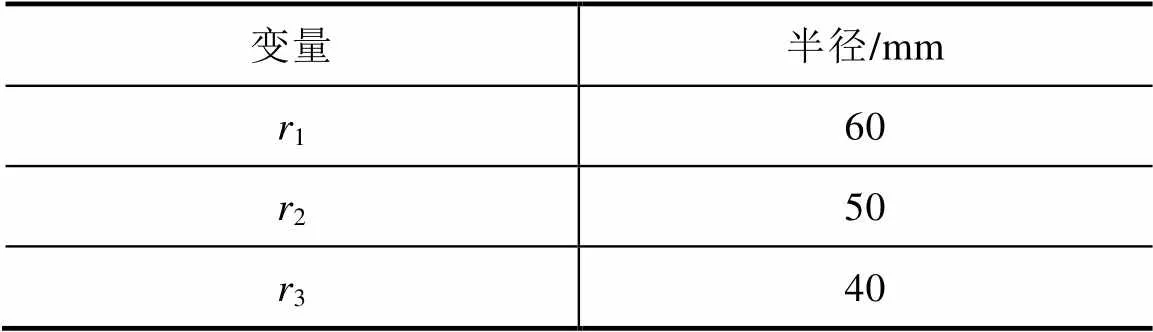
表3 不同半径
计算线圈在不同径向距离(平面方向)和纵向距离(轴正方向)下产生的磁感应强度,其分布曲线如图8所示。
图8可以看出:发射线圈半径的差异对磁场强度有着明显的影响。线圈半径从0.04m增加到0.06m过程中,当径向距离d<时,径向方向上的磁场强度在同一位置处随着半径增大而减小;当径向距离d>时,径向方向上的磁场强度在同一位置处随着半径增大而增大。原因是在线圈内部,半径越小,则磁通越密集,导致磁场强度反而增大。在线圈外部,由于空气介质,磁通量向外扩散没有约束,因此同一位置距离线圈较近,磁场强度较大。纵向方向上的磁场强度在同一位置随着半径增大而减小。其原因是轴上的每一点的磁场强度由每匝线圈产生的磁场强度的叠加,线圈半径的增大,线圈距离轴的距离增大,因此磁场强度减小。
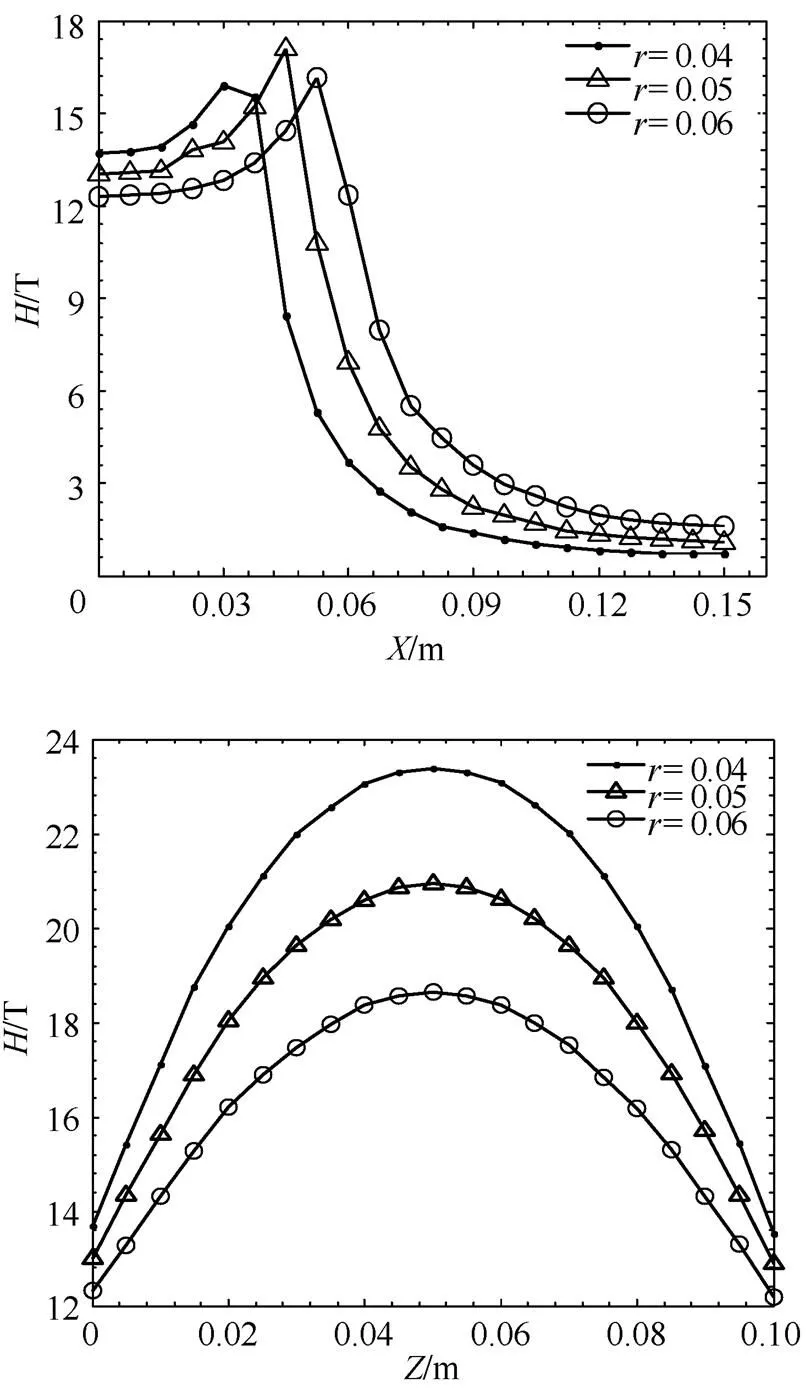
图8 不同半径下磁场强度H分布曲线
当一定时,径向方向的磁场强度在半径范围外随着径向距离的增大显著减少;纵向方向的磁场强度随着纵向距离的增大先增大后减小。磁场强度在=处有最大值。同时,随着线圈半径的增大,磁场的覆盖范围也增大。综合考虑,在物理尺寸允许的范围下,为了获得较强的磁场强度和范围较广的磁场,应选择半径较大的线圈,纵向方向的磁场的减弱可以通过增大通入电流来弥补。
4.2 线圈匝数对磁场强度的影响
设置线圈不同匝数,见表4。
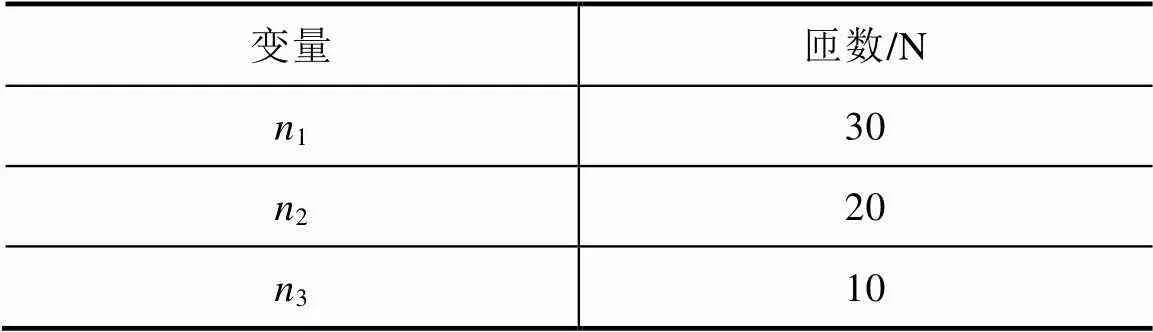
表4 不同匝数
在匝间距一定的情况下,线圈匝数的变化会导致线圈高度的变化。不同匝数的发射线圈在径向和纵向的磁场强度分布曲线如图9所示。
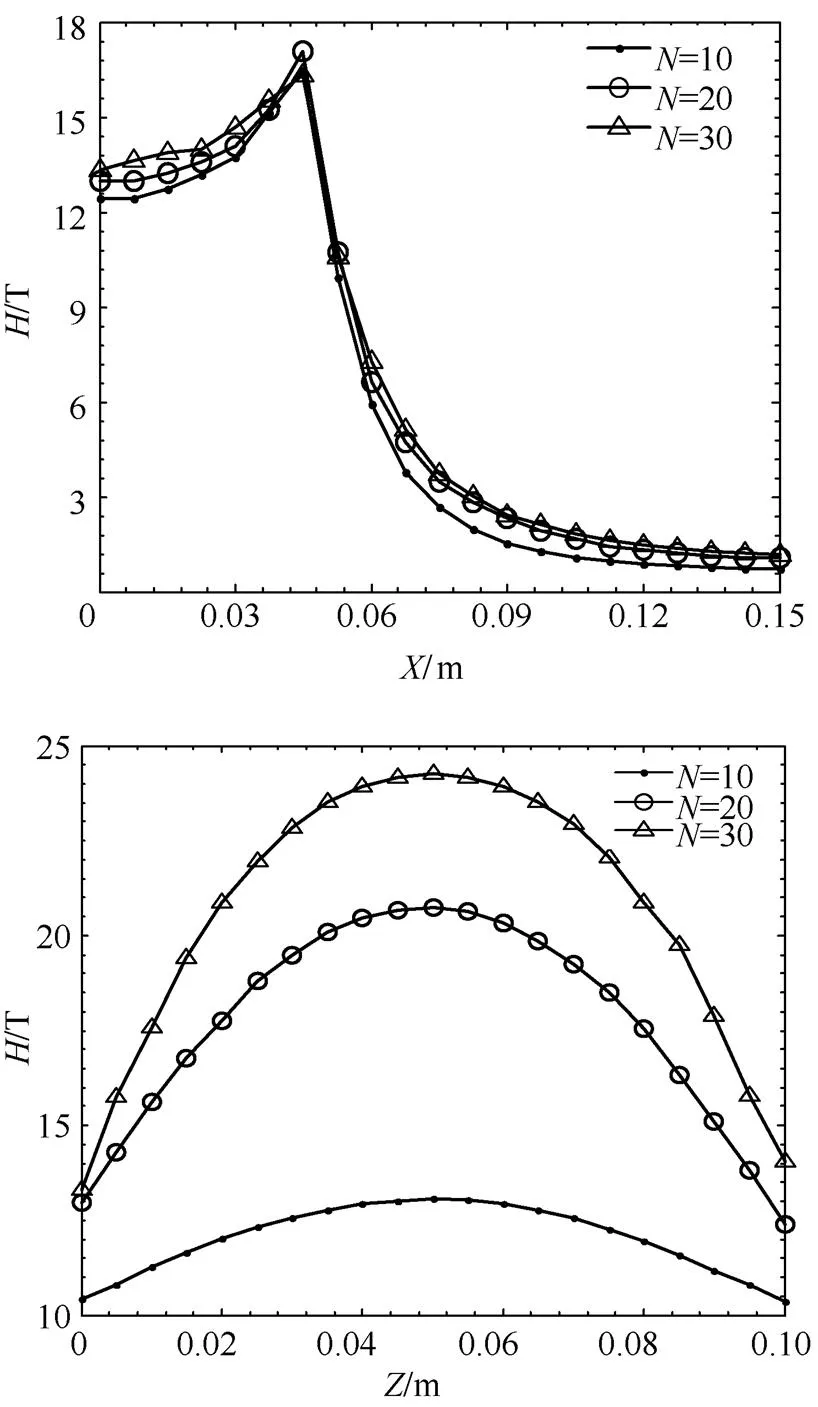
图9 不同匝数下磁场强度H分布曲线
从图9可以看出:线圈匝数从10N增加到30N过程中,径向方向的磁场强度在同一位置处几乎没有变化,而纵向方向的磁场强度在同一位置处随着匝数增加明显变大,并且在纵向上的磁通量辐射的距离也随着匝数的增加而变广。
当一定时,径向距离上的磁场强度随着距离的增大而显著减小,沿纵向距离的增大先增大而减小。磁场强度在处有最大值。综合考虑,虽然匝数的增加对径向距离方向上参数的磁场强度几乎没有影响,但线圈匝数会影响设计电路的电感,因此在设计WPT系统电路时,应该灵活考虑,满足电路要求。
4.3 线圈匝间距对磁场强度的影响
从目前各国对发射线圈的实际设计上来看,感应线圈在匝间距的设计上可采用密绕型和稀疏型,二者的代表性设计分别来自法国AREVA和INEEL[10]。设置线圈不同匝数,见表5。
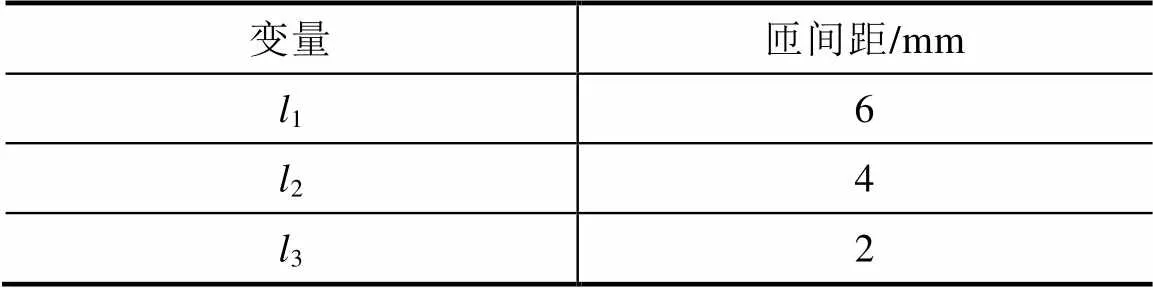
表5 不同匝间距
在匝数一定的情况下,匝间距的变化也会引起线圈总高度的变化。不同匝间距发射线圈在径向和纵向的磁场强度分布曲线如图10所示。
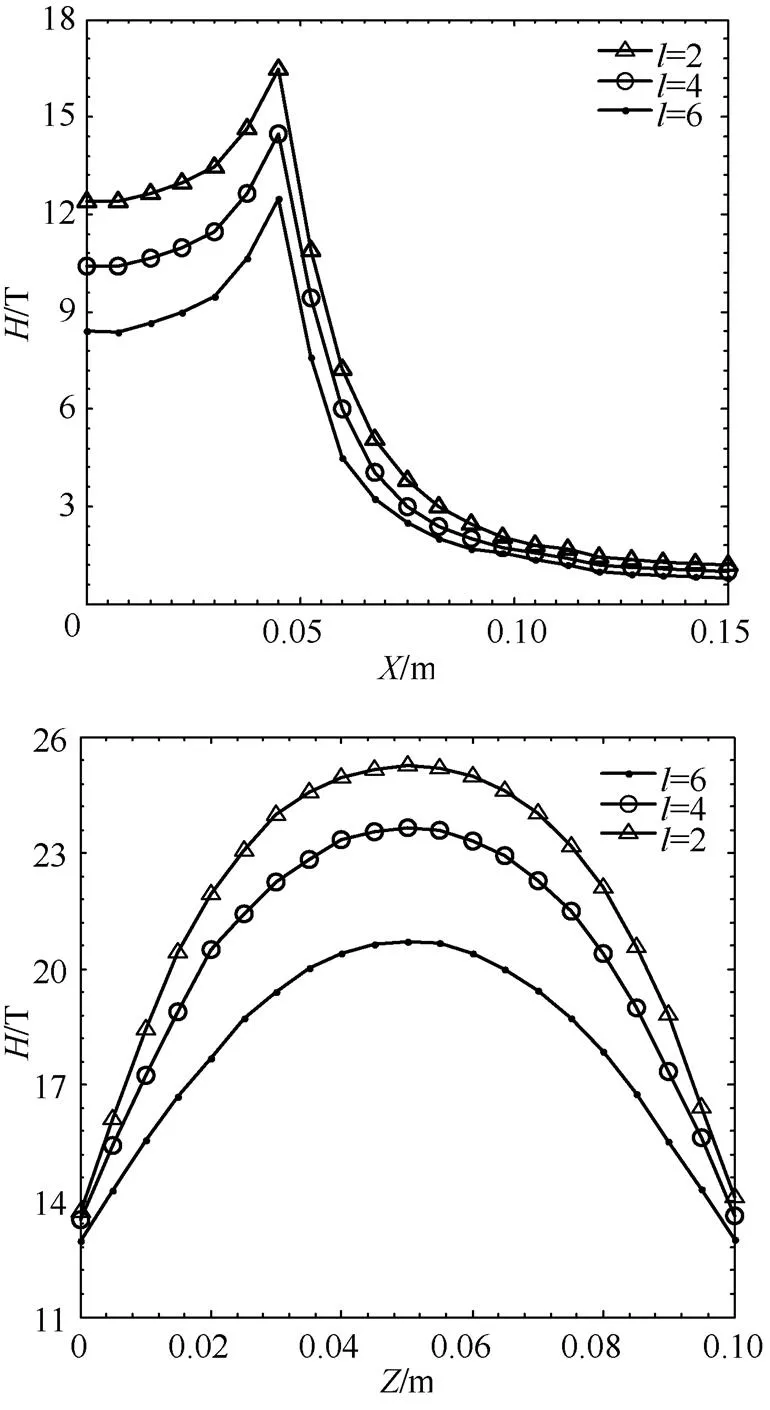
图10 不同匝间距下磁场强度H分布曲线
从图10可以看出:随着线圈匝间距从2mm增加到6mm,径向方向和纵向方向上在同一位置处的磁场强度均显著减小。这是因为径向或者纵向上任意一点的磁场强度由每匝线圈产生的磁场强度叠加和,匝间距的增大,使得相同位置距离其他线圈的距离变远,因此叠加的磁场强度减弱。
当一定时,径向距离上的磁场强度在半径范围外随着距离增大显著减小。纵向距离的磁场强度随着距离增大先增大后减小。在=m处,磁场强度均有最大值,同时,匝间距的增大使得线圈的总高度增加,磁场覆盖范围增加。综合考虑,匝间距的增大虽然增大了磁场覆盖范围,但对径向和纵向方向上的磁场强度有着明显的削减。因此在设计发射线圈时,应该尽量减少匝间距,建议根据实际情况考虑设计在2~4mm之间,而磁场的覆盖范围可以通过增加匝数来弥补。
5 结论
本文基于ANSYS软件对无线电能传输系统的发射线圈进行了有限元仿真分析,研究了线圈附近磁场分布的规律,并根据仿真数据利用Matlab软件绘制了磁场强度的曲线分布图,分析了感应线圈半径、匝数以及匝间距这3个设计参数对磁场的影响,得到以下结论:
1)线圈产生的磁场强度在径向上由线圈半径附近向两端衰减,纵向上线圈上下两端处磁场强度有最大值。
2)线圈半径的增大有利于增大线圈径向上的磁场强度,纵向上磁场强度有一定程度的衰减,可以通过增大通入电流来增大纵向上的磁场强度。
3)线圈匝数的增加对径向上的磁场分布几乎没有影响,由于线圈总高度的增加,纵向上磁场强度有所增大。在具体设计时还应考虑实际电路中匝数对线圈电感的影响。
4)线圈匝间距的增加会显著降低径向和纵向上的磁场强度。
综上几点考虑,在实际电路中,建议发射线圈半径设计尽量满足最大物理要求,匝数可根据电路特性自由选取,线圈采取密绕型绕法,建议匝间距为2~4mm。
[1] 卢文成, 丘小辉, 毛行奎. 磁谐振无线电能传输系统的最大效率分析[J]. 电气技术, 2015, 16(4): 14-17, 21.
[2] 高世萍, 麦瑞坤. 基于LC网络的感应电能传输系统动态供电方法[J]. 电气技术, 2018, 19(1): 20-23.
[3] 黄云霄, 张强, 牛天林, 等. 磁耦合谐振式无线电能传输系统线圈优化研究[J]. 计算机仿真, 2017, 34(10): 172-176, 304.
[4] 孙悦, 李云涛, 叶兆虹, 等. 三线圈ICPT系统中继线圈的位置优化[J]. 电工技术学报, 2016, 31(13): 172-179.
[5] Pere J M, Bickford D F, Day D E, et al. High-level waste melter study report[M]. Richland, WA: pacific Northwest National Laboratory, 2001: 58-60.
[6] Zhao J F, Huang X L.Wireless power transfer with two dimensiona lresonators[J]. IEEE Transaction on Magnetics, 2014, 50(1): 1-4.
[7] 张强, 牛天林. 磁耦合共振双发单收系统特性仿真分析[J]. 测控技术, 2017(36): 11.
[8] 李中启, 黄守道, 袁小芳. 线圈非同轴时磁耦合谐振式无线电能传输系统的效率优化[J]. 电工技术学报, 2017, 32(8): 151-159.
[9] 赵凯华, 陈熙谋. 电磁学[M]. 北京: 高等教育出版社, 2011.
[10] Zhong W X, Hui S Y R. Maximum energy efficiency tracking for wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 4025-4034.
Simulation analysis of magnetic field of three-dimensional wireless power transmission coil
Yu Chengbo Zhang Lin Zeng Liang
(Chongqing University of Technology, Chongqing 40400)
Induction coil act as an excellent wireless power transmitter,the magnetic flux density resulting is an important factor affecting the efficiency of its energy transfer. Therefore, in this paper, ANSYS was used to establish the 3D finite element model of induction coil and the edge-element method was used to solve the transmitting coil, the distribution of the magnetic field intensity of the transmitting coil is given. By changing the coil different design parameters such as coil diameter, coil turns and the distance of each turn of the coil, Analyze the factors that affect the strength of the magnetic field and change these key factors to enhance the magnetic field strength. The analysis results provide a theoretical basis for optimizing the induction coil.
induction coil; finite element; magnetic induction intensity
2018-03-20
余成波(1965-),男,教授,主要研究方向为电气设备故障在线检测与诊断、信号与信息处理、远程测试与控制技术。
重庆市研究生科研创新项目(CYS17279)
