带LCL滤波的基于状态空间控制的有源滤波器
2018-08-18郑成伟胡金高
郑成伟 胡金高
带LCL滤波的基于状态空间控制的有源滤波器
郑成伟 胡金高
(福州大学,福州 350108)
并联有源电力滤波器(SAPF)是一个典型的电流跟踪控制系统。在APF系统中引入LCL型输出滤波器对开关谐波有良好的衰减效果,但易发生谐振。本文探索了一种对补偿电流的快速跟踪及抑制谐振问题的新型控制方法。在同步旋转坐标系下进行复数形式下建立状态空间模型,可使有功无功解耦控制,且可直接分离获得谐波电流,实现APF系统由谐波检测和补偿控制两个环节的一体化;利用观测值反馈,通过状态反馈极点的配置,来改善系统的动态响应和稳定性,实现抑制谐振及减少阻尼损耗。在控制器设计中还综合了母线电压稳定和电网电压前馈环节。最后给出一些仿真结果,验证了该设计的有效性。
有源电力滤波器;LCL滤波器;状态反馈;降阶观测器;前馈补偿
绿色电网需要净化电网中的谐波,有源电力滤波器(APF)使用并网的逆变器来实现电网中的谐波的反向低效补偿。为了抑制逆变器功率开关器件产生的噪声谐波,需要在并网逆变器和公共电网有一个高效的滤波环节,如采用传统中的单电感滤波器,虽然结构简单,但是需要较高的开关频率或较大的电感才能满足要求,较大的电感增加系统的重量、体积与成本,而且降低了电流响应动态性能。为了克服单电感的缺点和不足,目前LCL型滤波器以其小型化、低成本以及优异的高频开关噪声抑制能力,成为系统研究的热点。
LCL滤波器是三阶系统,频率响应在谐振频率处存在谐振尖峰,同时相位发生-180°跳变,本身难以稳定控制。这就需要增加在谐振频率处的阻尼,一般有两种,即无源阻尼和有源阻尼。无源阻尼一般是在电容支路串联或者并联电阻,因其实现简单而被广泛应用。但是阻尼大小的设置在稳定性和损耗之间是相互矛盾的,且在高压大功率场合下,额外的阻尼损耗以及其带来的发热,会给应用带来较大的不便[1]。
同时,为了高次谐波的可控有效补偿,系统的动态响应频带也应该需要足够的宽度(如40次谐波,频宽就是40×50Hz=2kHz),这显然也是传统方法难以满足的,因此采用基于状态变量反馈的有源阻尼方法成为关注焦点。
以状态反馈为基础的控制理论中,通过合理选择反馈增益阵来改变对象的动力学特性,采用不同极点的配置,实现不同的控制效果,能有效解决LCL滤波器的谐振现象,并且相对于阻尼电阻,降低了系统的损耗。文献[2-4]中新型控制方法是建立在SAPF仿射非线性模型的基础上,通过状态反馈线性化后进行PI控制,简单容易实现,且动态性能优于传统方法。并且是利用坐标变换,在同步旋转坐标系dq下建模,实现了有功电流与无功电流,以及谐波电流与直流侧电压的解耦控制。然而,该新型方法是建立在L型滤波器模型基础上的,这种变换下d轴和q轴之间并不独立,存在交叉耦合关系;对于LCL型采用park变换,则由原来三阶微分方程变成六阶微分方程,这样增加了控制的难度,并不具有实用性。文献[5-7]是基于离散状态空间的LCL滤波器模型上,应用全状态反馈来抑制谐振,采用全阶观测器,在不增加传感器的基础上,实现良好的动态和稳定性能。为了解决稳态误差,文献[5]加入了PI环节;在文献[7]考虑到电网电压作为扰动必然会对系统补偿产生影响,加入了电网电压作为前馈,该方法是在给定电流为零时系统bode图中查看其在50Hz处的增益,以此系数进行适当操作,消除了电网输入的影响。
鉴于上述考虑,本文尝试基于状态变量反馈的有源电力滤波器系统控制,在同步旋转dq坐标系下进行复数形式下的数学模型建立,模型仍是三阶系统,在d、q轴下独立控制,巧妙的实现了有功和无功的解耦。
补偿电流控制器设计是SAPF的核心,其是在全状态变量反馈基础上,综合了给定电流以及电网电压前馈控制,设计出谐波电流跟踪控制器,增加了系统的阻尼,抑制LCL环节的谐振,实现无损耗的有源阻尼以及快速响应;控制律中加入的电网前馈解决了稳态误差。其次,全状态变量控制增加了传感器应用,设计合理的降阶观测器,预测状态变量。由于SAPF逆变器的直流侧一般采用直流电容作为储能环节,所以通过dq坐标系下的附加直流有功分量能方便地维持直流侧电压的恒定。
1 带LCL滤波的并网式逆变器系统及建模
1.1 系统建模
图1所示为基于LCL滤波器的SAPF系统的主电路拓扑。
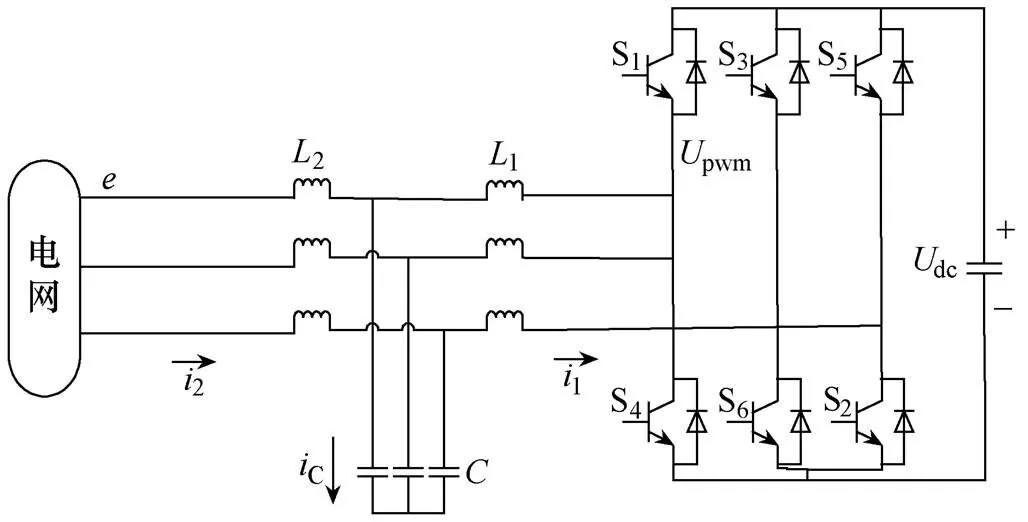
图1 基于LCL型滤波的并网式逆变器
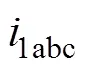
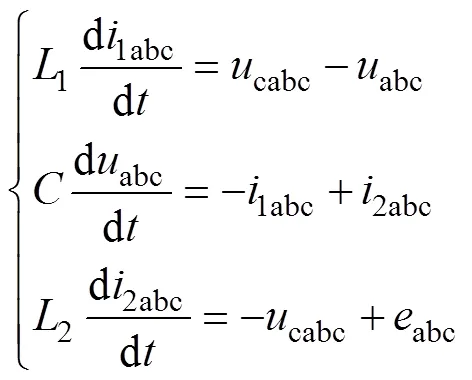
三相abc静止坐标系下需要控制的量很多,且被控量均为交流量,为了降低三相系统的控制的难度,同时考虑逆变器采用的空间矢量的控制方便性,一般将其转换到两相dq同步旋转坐标系下成为两相直流量。首先通过Clarke变换,可以将abc静止三相坐标系转换到两相ab静止坐标系下,微分方程形式保持不变。
在两相ab静止坐标系下,a轴为实轴,b为虚轴,则各个状态矢量可以表示成复数形式:
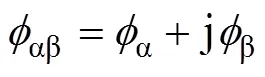
两相静止坐标系以电网同步频率进行旋转,则得到旋转dq坐标系,即。
因此,得到同步旋转坐标下复数形式的微分方程为
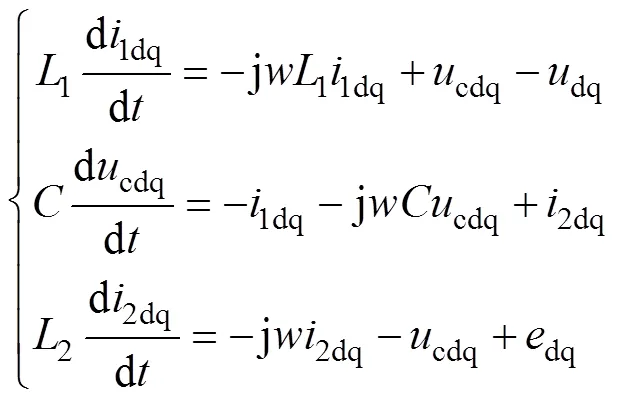
为了方便简洁,在本文以后下标dq将不再标注。
由该状态方程可以得到并网逆变器LCL滤波器的状态空间方程:
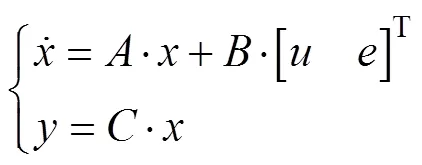
其中:
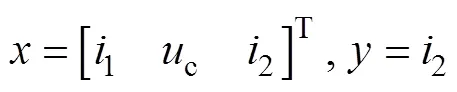
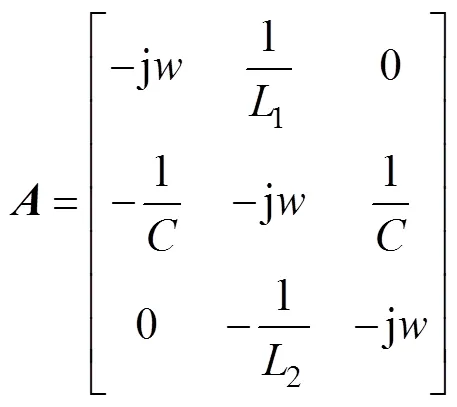
对上面的状态空间方程离散化后,可得
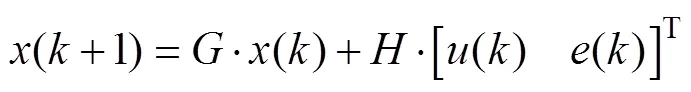
1.2 解耦
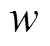
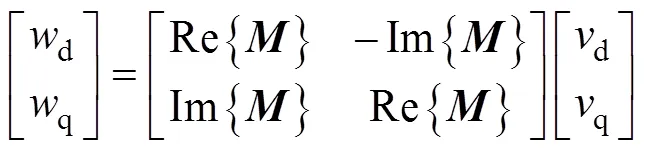
这个过程可以用如图3所示。
2 基于离散化状态空间的控制器设计
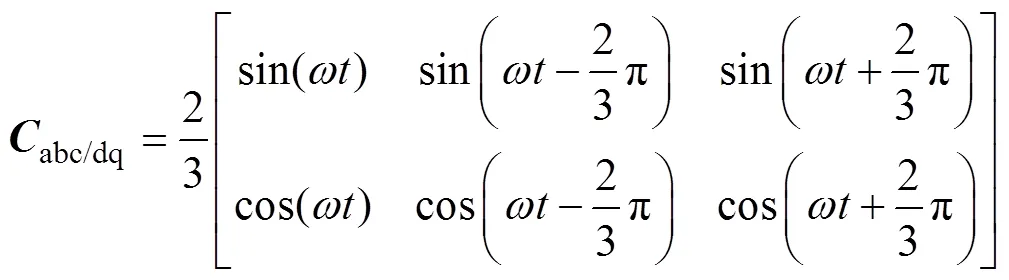
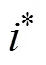
2.1 设计状态反馈律
首先设计一个状态控制反馈控制律,即
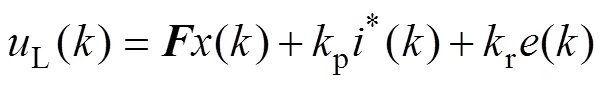
LCL是三阶欠阻尼系统,因此本文采用基于状态反馈的有源阻尼方案,通过任意不同极点的配置,实现不同的控制效果,有效解决了LCL滤波器的谐振现象,相对于阻尼电阻,降低了系统的损耗。
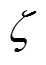
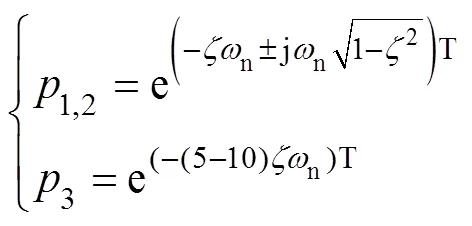
将式(8)代入式(5)中可以得到
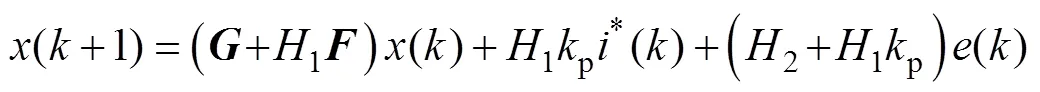
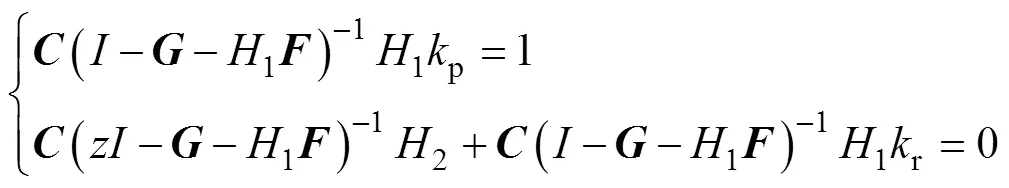
由上式可得
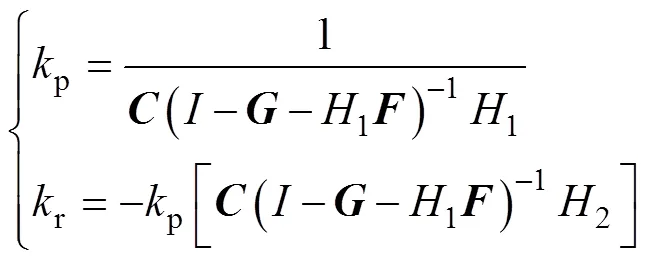
2.2 设计降阶观测器
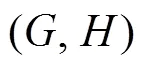
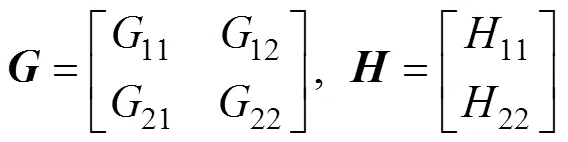
得到观测器为
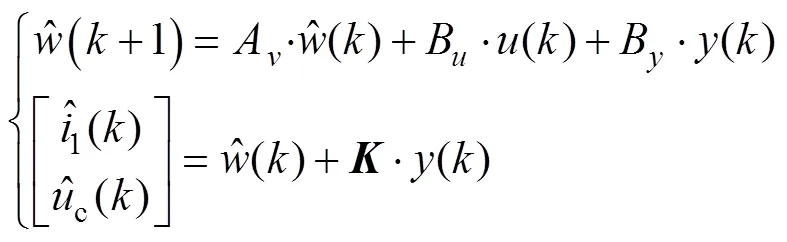
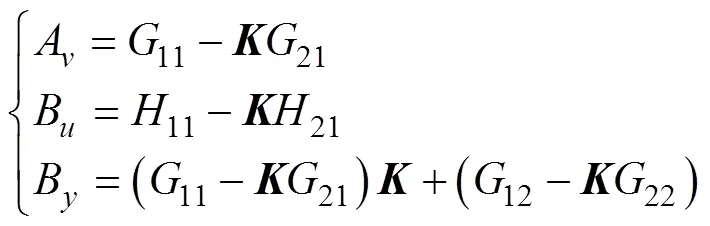
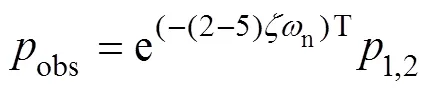
2.3 对控制律及观测器进行综合
将控制律以及降阶观测器合并成为最终的控 制器,即
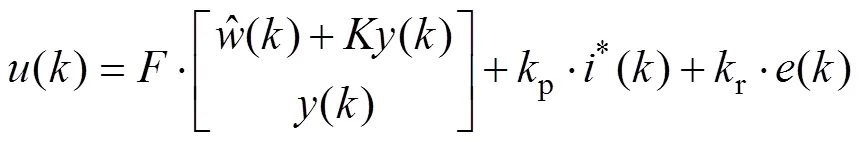
控制器结构示意图如图4所示。
3 有源滤波器的搭建与仿真分析
依据上述思路,可以搭建如图5所示的并联型有源电力滤波器系统框图。
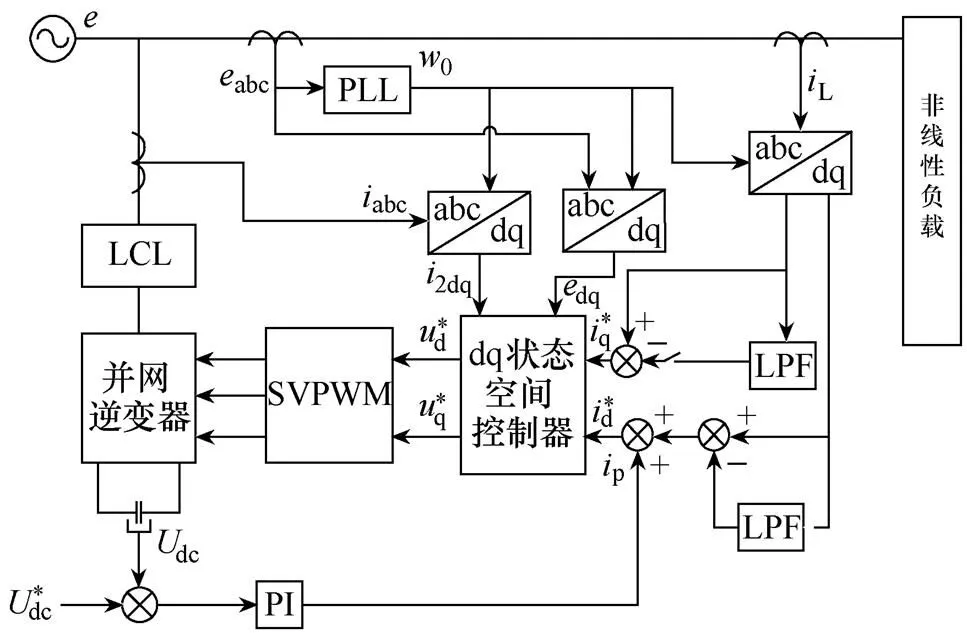
图5 基于状态空间的一体化测量与控制框图
3.1 电网谐波的测量
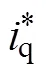
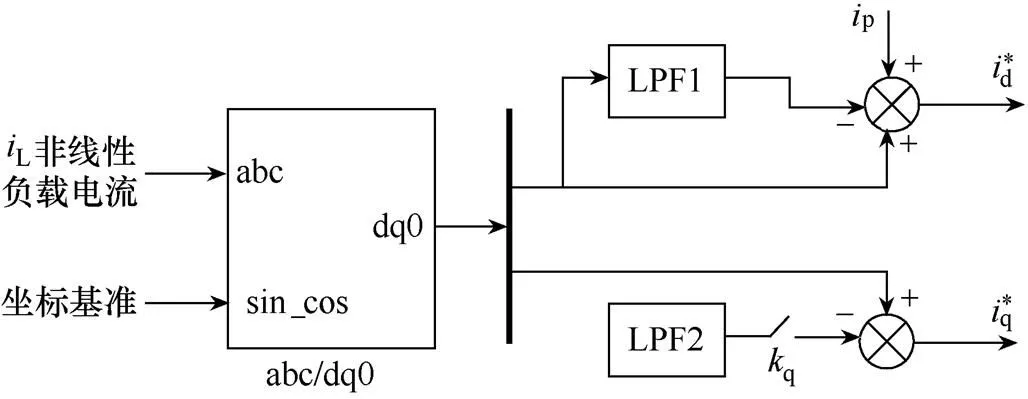
图6 非线性负载的谐波检测与控制给定
这样使APF控制系统中两大组成部分在一个统一的环节中完成,较好实现了检测-控制一体化。图7为三相不可控整流桥负载下,在0.30s时直流负荷从100A变成200A时的q检测波形。
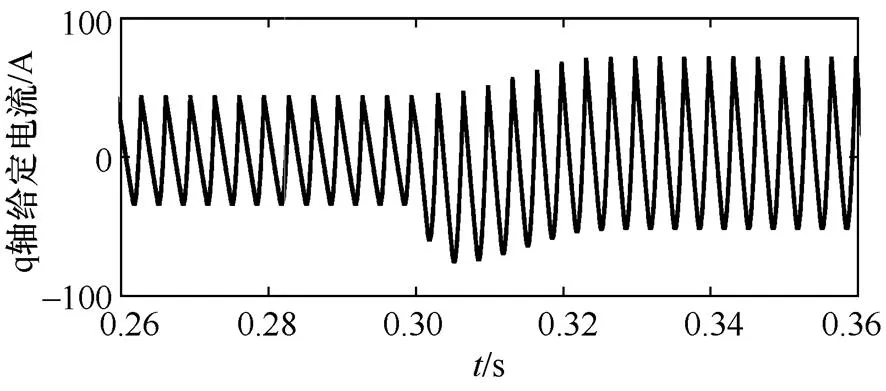
图7 整流桥负载下Iq检测到的谐波波形
3.2 直流母线电压的稳定控制
补偿电流的时变性以及开关损耗等会使逆变器的直流侧电容电压产生波动,这将会影响SAPF的谐波补偿性能。在图5中,在dq坐标系下同样可以注入附加的有功直流分量p来稳定直流侧电压。p为稳定母线电压需要电网加入有功功率。采取简单的PI调节电压闭环控制,在电压过低时注入+p,在电压过高时注入-p。如图8所示,电压过低注入+p,0.2前为预充电和泵升过程,电压稳定之后分别在0.2s和0.3s突加负载,直流侧母线电压能够快速调整并趋于稳定。
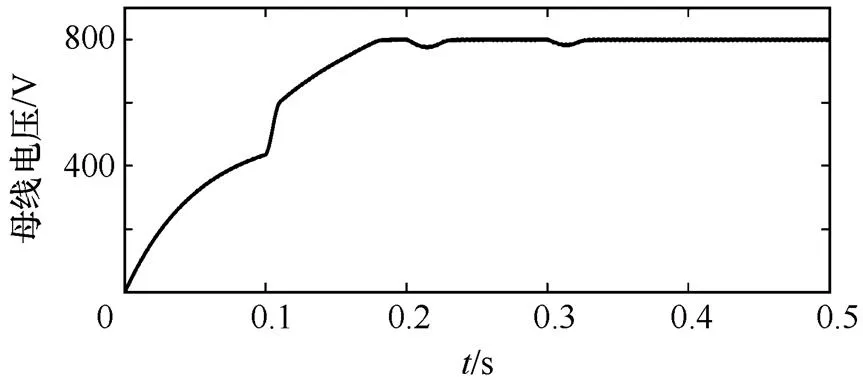
图8 直流侧母线电压波形
3.3 系统仿真波形分析

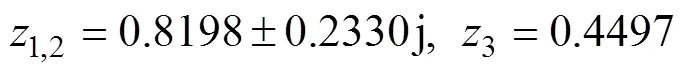
则按照上述设计的控制律计算得

接着,观测器极点在域的实部是系统极点实部的2.1倍,虚部保持一致,即观测器极点取为
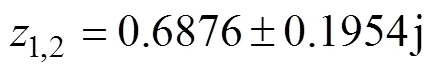
得观测器增益为

按照设计式(15),可得到观测器方程为

为验证控制器的控制率,得出以下仿真波形,如图9所示,补偿前带有谐波的负载电流通过补偿电流的补偿后电流波形接近正弦波。由图10所示的电流频谱图可以得到,经过SAPF补偿后,畸变率由原来20.71%降低为4.84%。
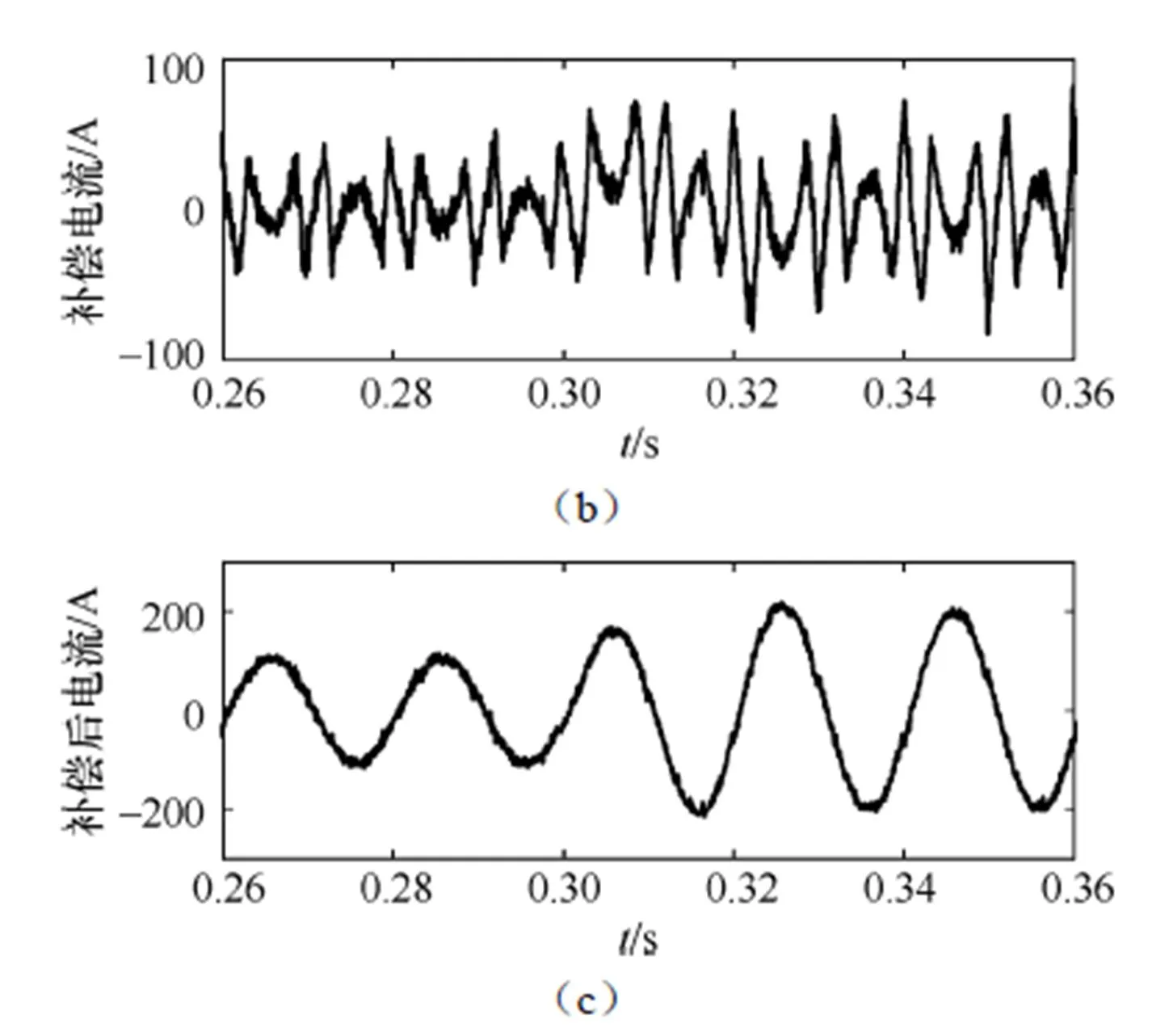
图9 A相补偿前电流、补偿电流及补偿后电流波形
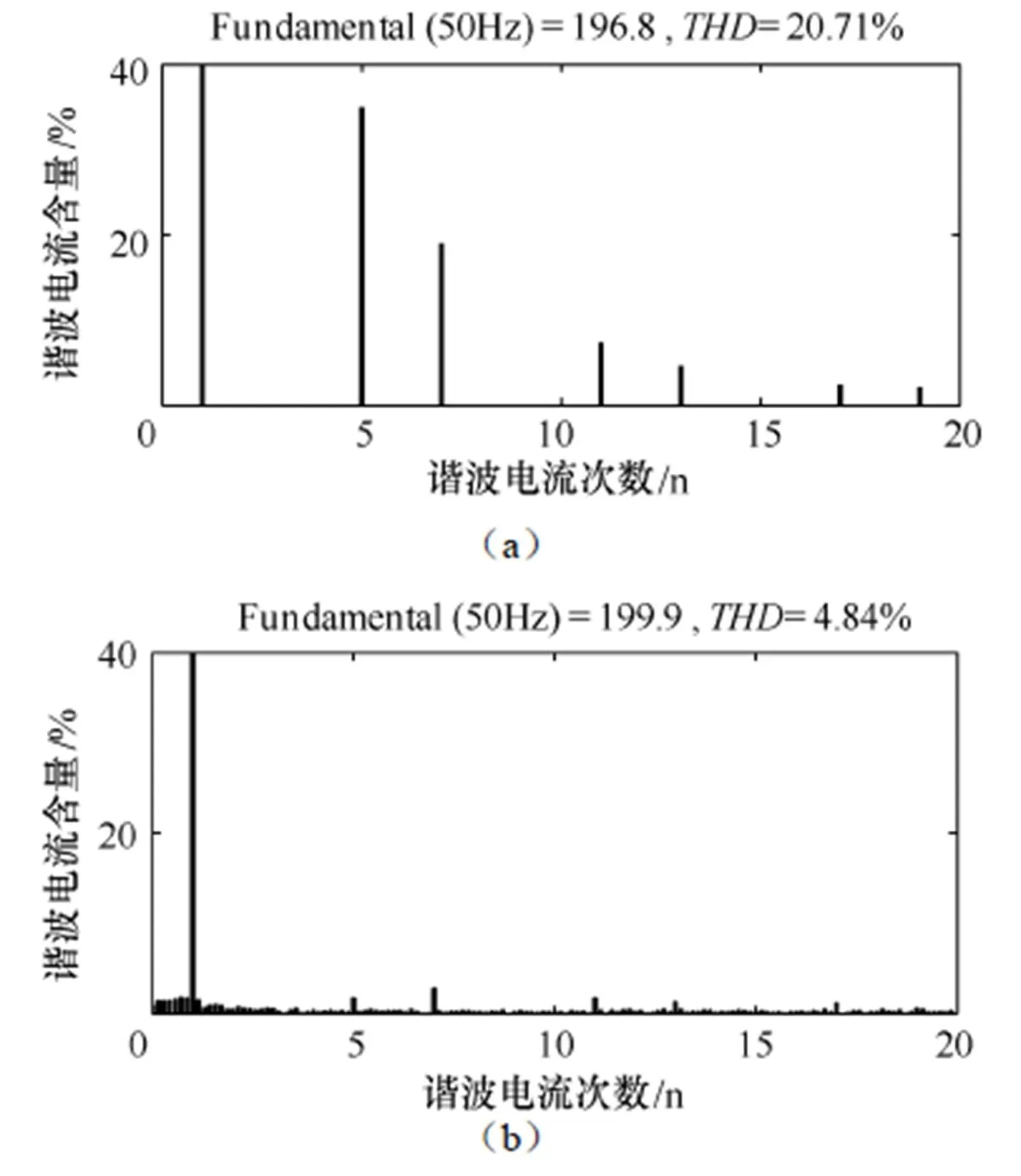
图10 A相补偿前后电流频谱图
4 结论
本文提出了一种新型的APF控制方案,该控制律是在复数状态空间矩阵基础上,引入了给定参考和电网电压扰动的前馈补偿,并利用降阶观测器减少传感器的使用数量,用于跟踪负载谐波和无功电流,使补偿电流与负载中的谐波和无功电流相抵消。并在Matlab/Simulink中进行了仿真实验。结果表明,提出的控制律能较好地抑制LCL滤波器的谐振现象,系统在负载稳态下时,有良好的电流补偿性能。在负载突变的情况下,网侧电流和直流母线电压都能快速跟踪响应。
[1] 王兆安, 杨君, 刘进军, 等. 谐波抑制和无功功率补偿[M]. 北京: 机械工业出版社, 1998.
[2] 乐江源, 谢运祥, 张志, 等. 有源电力滤波器状态反馈精确线性化控制[J]. 电力自动化设备, 2010, 30(2): 81-85.
[3] 王一军, 吴伟标. 一种新型的并联有源滤波器非线性解耦控制方法的研究[J]. 现代电力, 2012, 29(1): 37-41.
[4] 陈兆岭, 杨辰星, 刘国海. 新颖的有源电力滤波器复合控制方法[J]. 电测与仪表, 2013, 50(3): 69-74.
[5] 谷雨, 陈国柱. 基于状态空间的电力有源滤波器控制策略[J]. 机电工程, 2008, 25(7): 76-79.
[6] 侯朝勇, 胡学浩, 惠东. 基于离散状态空间模型的LCL滤波并网变换器控制策略[J]. 中国电机工程学报, 2011, 31(36): 8-15.
[7] 李宾, 姚文熙, 杭丽君, 等. 基于状态观测器的LCL滤波器型并网逆变器状态反馈最优化设计[J]. 电工技术学报, 2014, 29(6): 80-90.
[8] Kato T, Inoue K, Donomoto Y. Fast current- tracking control for grid-connected inverter with an LCL filter by sinusoidal compensation[C]//Energy Conversion Congress and Exposition (ECCE), 2011 IEEE: 2543-2548.
[9] Mingyong Cui, Rui Yao. Input-output feedback linearization control of grid-connected inverter with LCL filter[C]//Renewable Power Generation Conference (RPG 2013), 2nd IET Year: 2013: 1-5.
[10] 郭邵卿, 何星晔, 朱鸥, 等. 改进的谐波电流检测法及其在有源滤波器中的应用[J]. 电气技术, 2015, 16(7): 84-87, 102.
[11] 况秋霞, 胡金高. SAPF在不同补偿方式下的直流侧电压取值分析[J]. 电气技术, 2015, 16(1): 27-31, 35.
[12] 许胜, 费树岷, 赵剑锋, 等. 多模块APF并联系统高频谐波环流分析与控制[J]. 电工技术学报, 2016, 31(5): 60-68.
[13] 张雨潇, 戴珂, 陈新文, 等. 检测电流包含电容电流的SAPF谐波抑制和谐振阻尼新方法[J]. 电工技术学报, 2017, 32(S1): 58-67.
The active filter with LCL filtering based on state-space control
Zheng Chengwei Hu Jin’gao
(Fuzhou University, Fuzhou 350108)
Shunt active power filter is a typical current tracking control system. The output LCL filter used in APF has a good damping effect to switch harmonics, but is prone to resonance. This article explores a new control method for fast tracking of compensation current and suppressing resonance. The complex form of state-space model is first established in the synchronous rotating d_q coordinate, which can make the active and reactive power components decoupled, and at the same time the harmonic current can be directly extracted, thus the harmonic detection and compensation control in the APF system are unified in the same realization. Using the observer-based feedback, the dynamic response and stability of the system can be improved through pole placement in state feedback, while effectively suppressing resonance and reducing the damping loss. Also incorporated into the main controller design are the stabilization of the DC-link voltage and the feed-forward compensation of grid voltages. Finally some simulation results are given to verify the effectiveness of the design.
active power filter; LCL filter; state feedback; reduced-order observer; feed-forward compensation
2018-01-16
郑成伟(1992-),男,硕士研究生,从事控制理论与控制工程方面的研究工作。
福建省自然科学基金(2017J01747)
