分布式发电系统中同步发电机励磁系统的动态性能对比
2018-08-18杨希刚刘爱军
曹 沂 杨希刚 刘爱军
分布式发电系统中同步发电机励磁系统的动态性能对比
曹 沂 杨希刚 刘爱军
(国电科学技术研究院有限公司,南京 210023)
本文比较分析了分布式发电系统中的同步发电机几种励磁系统动态性能,对系统的/关系变化、短路电抗、故障清除时间、最大有功功率和电压曲线进行了仿真分析,并对其性能进行了讨论。结果表明,静态励磁系统抗动态干扰性能更好,维护成本更低。从应用性方面讲,静态励磁系统相对于其他励磁系统更具优势。
分布式发电;同步发电机;励磁系统;动态性能
分布式发电系统应用日益广泛,尤其是同步发电机型[1]。励磁系统为发电系统重要的组成部分[2],主要供给同步发电机所必需的励磁,维持发电机的机端电压稳定,改善同步发电机运行的稳定性。同步机型发电机系统框图如图1所示。
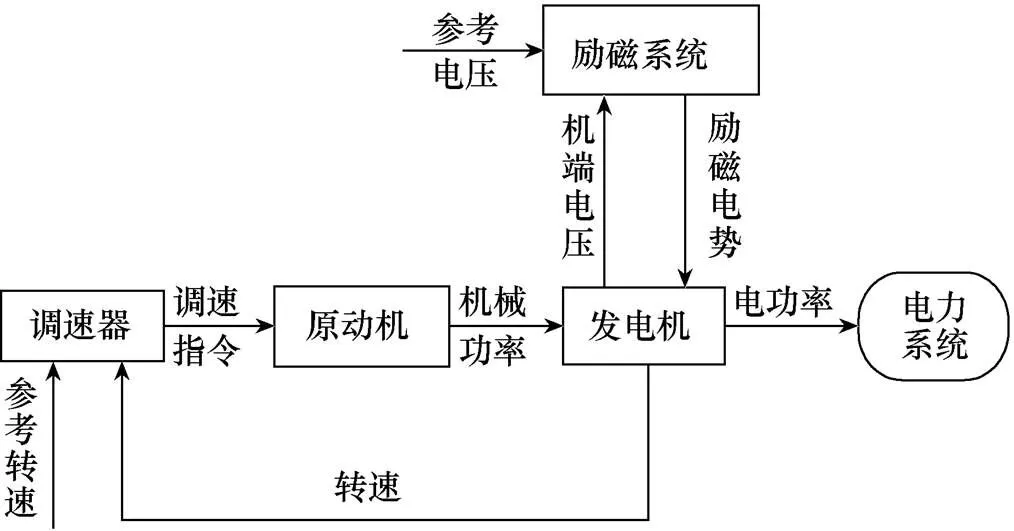
图1 同步机型发电机系统
分布式同步发电机中常见励磁系统配置类型 有[3]:①直流励磁系统,其代表是IEEE DC1A模型,主要用于工业;②无刷交流励磁系统,其代表是IEEE AC1A模型,利用率最高;③静态励磁系统,其代表是IEEE ST1A模型,技术性能高,维护成本低[4-5];④复合励磁系统,其代表是IEEE ST2A模型,在石油和天然气发电厂广泛使用。本文基于Matlab/ Simulink环境,对分布式发电同步机型励磁系统模型开展了仿真研究,考虑以下因素:
1)更改系统的/关系。
2)短路电抗。
3)不计发电损失的故障清除时间。
4)电机可以在不损失稳定性的情况下注入系统的最大有功功率。
5)同步发电机端子电压曲线。
1 仿真模型
本文使用Matlab/Simulink平台附加的SIMPOWERSYSTEM软件包进行仿真,使用POWERGUI作为初始化工具。电力系统组件由三相模型表示,采用电磁仿真,网络变量由瞬时值表示。系统组件模型见表1。

表1 Matlab/Simulink组件
在动态稳定性仿真期间考虑了表示为恒定阻抗的静态负载。另外,在电压稳定情况下还使用异步电机动态模型进行仿真[6-7]。
1)同步发电机模型
使用八阶模型(次暂态模型)来表示同步发电机,其在仿真研究中被减少到六阶模型,忽略定子瞬变。用实际的18.75MVA发电机进行仿真。
2)励磁系统模型
对于连接到配电网络的同步发电机励磁系统,通常可用两种控制形式,即恒定电压或恒定功率因数(无功功率)[8-9]。本文仅考虑最常用的恒压控制策略。
IEEE DC1A型的励磁机表示现场控制直流换向器激励器,具有连续作用的电压调节器。其在行业里获得广泛应用,并且在详细数据不可用或需要简化模型时用于表示其他类型的系统[10-11]。IEEE DC1A模型如图2所示。
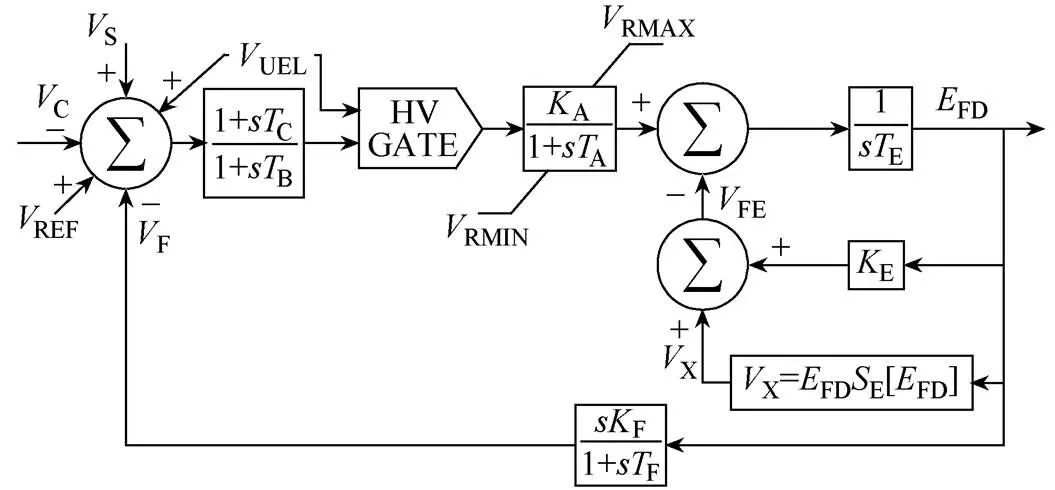
图2 IEEE DC1A模型
在求和点,从设定值参考REF减去实际端子电压C和稳定反馈电压F,所得到的信号在调节器中通过时间常数A和增益A放大。励磁饱和曲线通过X信号并入。通过使用发电机励磁电流FD来表示励磁器对负载的显著影响。交流励磁机输出端的二极管特性保证了励磁机输出电压下限为零。模型对整流器调节曲线EX、以及由整流调节C和励磁机同步和瞬态电抗D引起的励磁机输出电压降都进行了解释。IEEE AC1A型的交流励磁机如图3所示。在大型电力系统稳定性研究中,该模型被广泛用作无刷系统。

图3 IEEE AC1A模型
励磁系统还能够不使用旋转激振器就为发电机领域提供必要的直流电流。因此,该系统被称为静态系统。在静态系统中,无论是受控源还是非控制源,电压都可以通过整流器转换到适当的电平。
电势源控制整流器励磁系统模型(IEEE ST1A静态系统模型)如图4所示。模型展示IEEE ST1A系统通过变压器从发电机端子或发电单元的辅助总线提供励磁功率并由受控整流器调节。
这种系统可获得的最大励磁电压与发电机端电压直接相关。电压调节器增益和励磁系统时间常数分别由A和A表示。由于桥式整流器的触发角信号对于大多数系统是线性的,所以A是线性值。一些静态系统利用发电机电流和电压源来构成电源。根据相量组合,IEEE ST2A励磁器模型代表这种复合源整流器励磁系统。
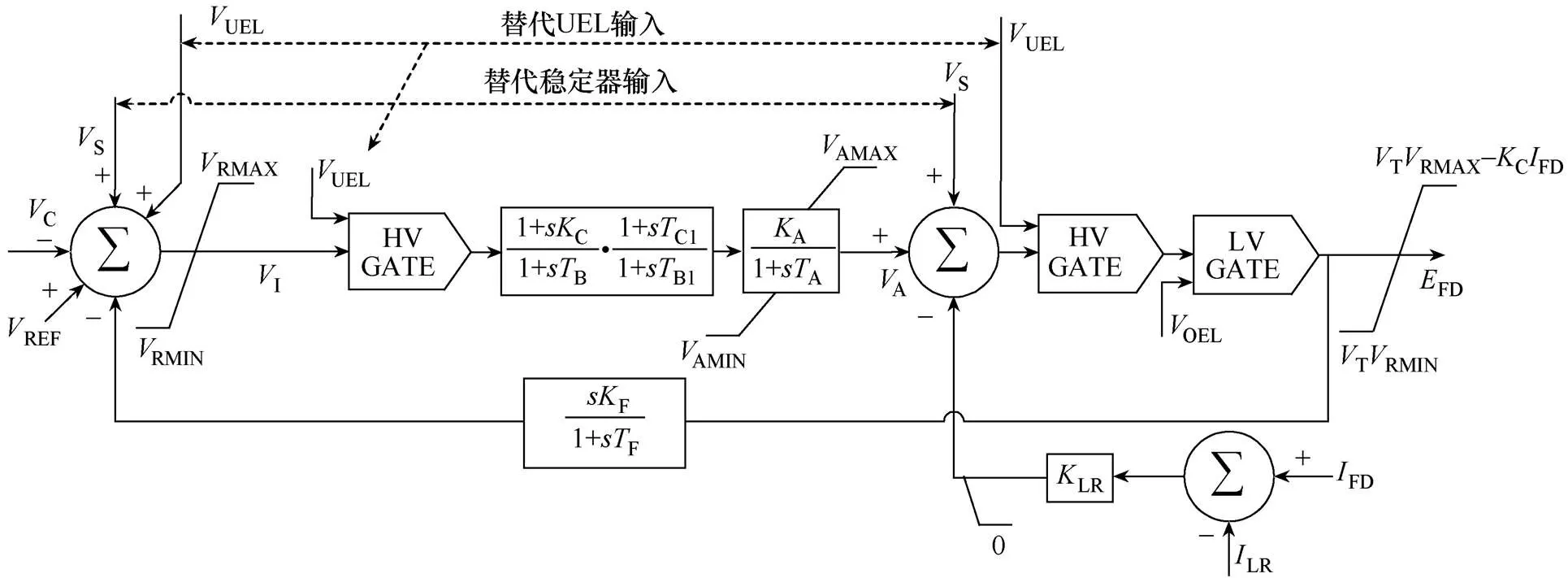
图4 IEEE ST1A模型
图5所示模型的应用主要与大用户相关。主发电机端子附近的馈线发生短路可能导致发电机保护动作引发停电,从而导致维护成本上升,停机时间延长,进而降低了用电可靠性。因此,复合系统的概念是指通过使用短路电气特性或负载突变(即发电机端子电压和电流)以及为此专门设计的复合变压器来馈送主机场或励磁机。整流器加载和换向效果表示为EX函数。
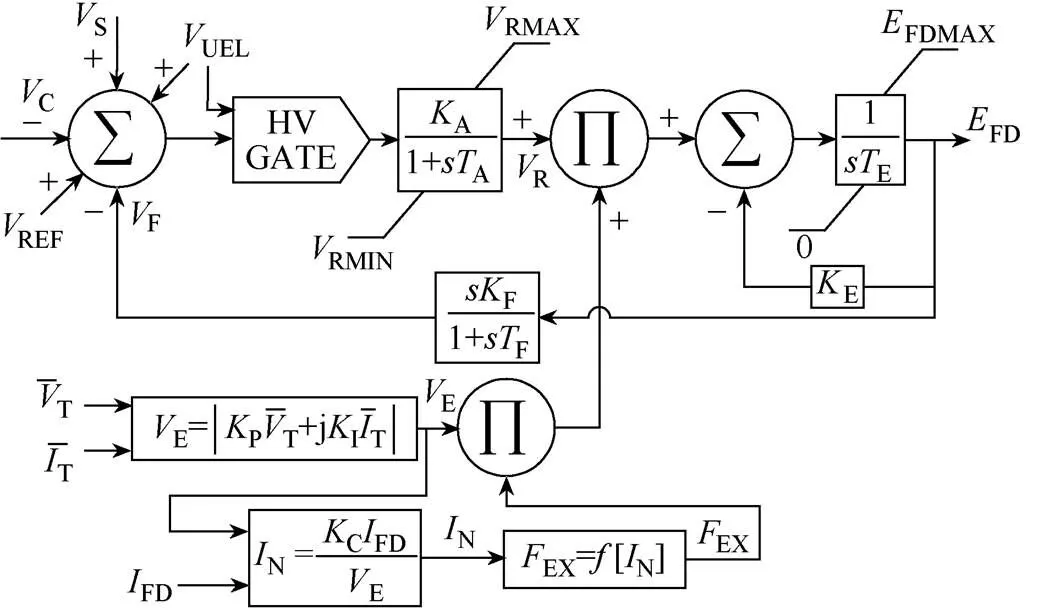
图5 IEEE ST2A模型
2 仿真结果
1)故障清除时间(CRIT)
本节的仿真和计算结果均考虑了在靠近同步发电机终端发生三相短路时同步发电机可以不失步而继续运行的时间。对每种励磁系统都分别进行了连续故障清除时间计算的仿真,其结果见表2。
因为故障发生在发电机端子附近,所以故障清除时间的仿真结果值较低。对于DC1A、AC1A和ST1A,也出现了类似的情况,ST2A具有更好的性能。事实上,这种性能在用作保护目的时可能并没有优势,因为电机与配电网并联,最容易造成电力系统故障。

表2 临界故障时间
2)最大有功功率(CRIT)
与配网中同步发电机的安装相关的一项重要研究证明最大发电机有功功率应注入网络节点,就不会在网络或发电机附近的干扰中失去稳定性。对短路持续时间为200ms的系统进行分析,并且再次监视电机转子角度直至系统失稳,其结果见表3。

表3 最大有功功率
在仿真中,ST2A的性能比DC1A、AC1A和ST1A更好,在所有负载水平下都能提供较低的电机故障角。ST2A在相同加载点处对所有的配置施加了离散的较高的场电压值。这有助于其在其他有效功率值以上的稳定性损失(面积标准)和相同负载水平下的离散较低的预失真角度[12]。这只是理想状态下的结果,实际上达不到。为了研究方便,总是忽略发电机损耗,所有配置都能够超过能力曲线的5%。
(2)与大豆产量挂钩的补贴政策效果不会改善政策的经济效率。根据国家发改委文件,大豆目标价格取消后会实施和玉米一样的生产者补贴政策,即实施与种植面积或产量挂钩的补贴政策。挂钩的补贴政策同样会产生扭曲,而且进口依存度越大产生的扭曲越大,政策的经济效率越低。实质上目标价格政策就是一种差价补贴,在市场环境没有发生改变的情况下,若取消目标价格政策转而实施与大豆产量挂钩的补贴政策仍不会提高政策的经济效率。
3)转子角度与故障清除时间
只要被检测到并消除的故障是由转子角造成的,转子角瞬态响应值就会增加。因此,同步发电机将会变得更加紊乱,这可以在所有配置中看到。图6显示了DC1A的转子角度具有不同故障清除时间。仿真表明,ST1A配置具有最高的转子角,因为它的时间常数较小。此外,其暂态响应非常快。
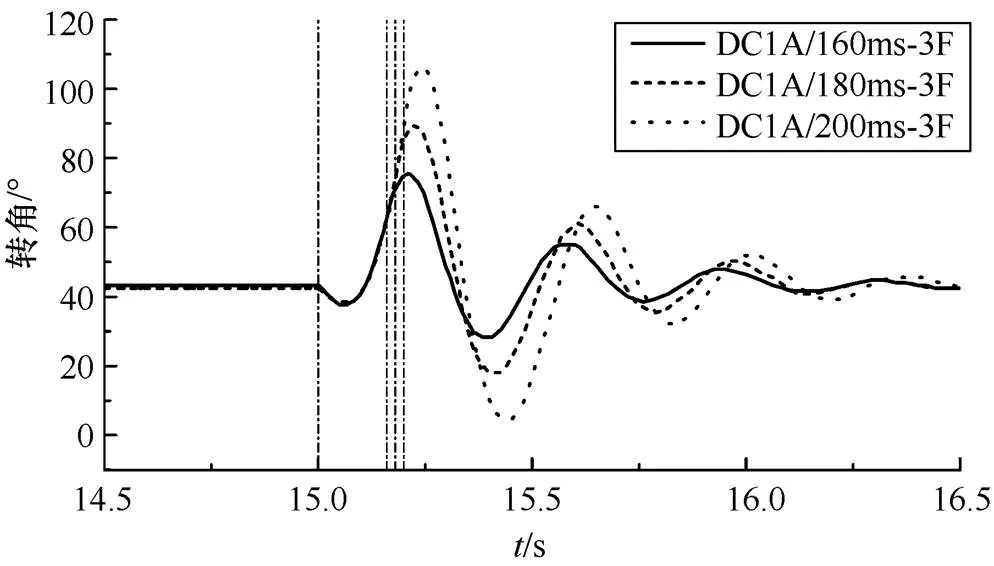
图6 转子角与故障清除时间
4)转子速度偏差与故障清除时间
发电机阻尼率由仿真中的动态特性得到。为确保得到预期的有功功率的振荡阻尼流,期望发电机阻尼率在每种情况下具有最高的可能值。停止振荡所需的时间取决于发电机自然和系统阻尼的值。在仿真过程中,转子速度振荡被视为二阶动力系统,为了估计阻尼比,对每条曲线采用对数递减法[13]获得两个对应于顶部和底部包线的阻尼率。对同一个指数,计算这两个阻尼率的算术平均值。
一般来说,随着故障清除时间的增加,阻尼率的降低,同步发电机的波动会变得更大。ST1A和ST2A配置的性能与DC1A和AC1A在任何时候都非常相似,如图7所示。

图7 转子转速偏差率与故障清除时间
5)转子角度与系统短路能力
短路电抗是与配电系统相关的重要因素,因为当发生诸如负载变化大、故障严重等干扰的情况时,短路电抗对配电系统稳定性有重要影响。在配电网络和输电网络互连的电路中,对3种不同的短路电抗进行了仿真。传输功率依次为500MVA、3500MVA和9500MVA,故障清除时间为200ms。在3500MVA和9500MVA下获得的ST1A的仿真结果如图8所示。

图8 系统短路电抗的转子角
总体结果表明,在同样条件下,系统短路电抗越低,故障后角度值越高,从而增加发电机失步的概率。由于发电机贡献必须随着系统短路电抗的降低而增加,所以其动态性能将会恶化。
DC1A、AC1A和ST1A配置与最小系统贡献500MVA非常相似。所以,与具有交流或直流励磁器的励磁系统相比较,ST1A具有较低的时间常数和快速响应时间。
仿真结果显示ST2A配置在所有电压水平下的故障后转子角度更低,这可以再次通过离散的较低的预故障角度来解释,因此不能代表相对于其他配置具有更好的动态反应[14-15]。
6)转子速度偏差与系统短路能力
由于通常发电机对维持短路影响最大,所以随着短路电抗的降低,阻尼率也随之降低。在500MVA短路电抗下,ST1A具有最高的转子速度偏差,这确保了较低短路能力的电气系统也能从ST1A获得更好的响应,如图9所示。此外,DC1A和AC1A配置对于相同的短路电抗具有较低的转子速度偏差,这表明即使具有高时间常数(时间常数作为主发电机和励磁机的总和),ST1A的性能也是最差的。对于更高的短路电抗,ST1A与ST2A的性能相似。
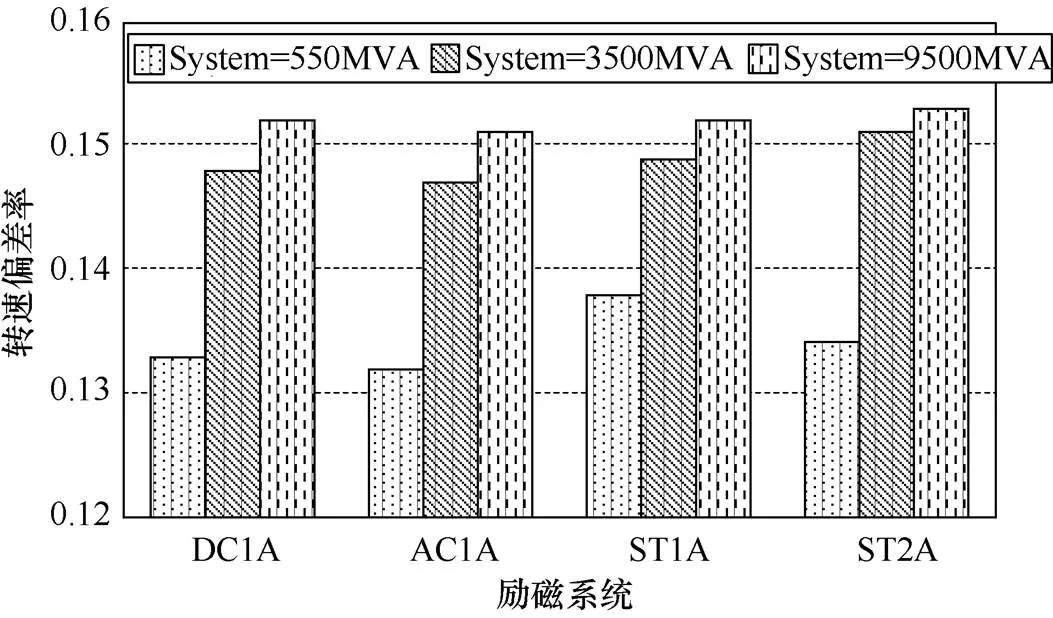
图9 转子转速偏差率与系统短路电抗
7)转子角度与系统/
/比是与分布式发电相关的一个重要因素,因为在系统中,较低的/比值不允许考虑q和V形式的去耦系统,所以励磁系统对无功电压(系统节点电压)和损耗都有影响。在配电网和输电网络互连的3个/比下进行仿真。故障清除时间依然设定为200ms内。
当/比值从0.5增加到接近3.0(基本情况)时,所有配置的转子后故障角最大值都有所下降,因为电力系统对于短路故障影响更大。与预期相反的是,随着/比从3.0增加到0.8,故障后转子角也增加了。
在相同的短路能力和短路电抗下,/变化导致也发生了变化。/比值的增加导致仿真过程中/对值的影响减小,从而表征扰动发生在发电机附近。因此,发电机失步还取决于同步发电机(其励磁系统)对扰动时间的损耗的贡献。
8)转子转速偏差与系统的/
在仿真时观察到,在3个/值(0.5、3.0和8.0)处,ST1A配置呈现闭合比,这表明ST1A优于其他配置。此外,其性能接近ST2A,一般优于DC1A和AC1A。
3 结论
经过对不同励磁系统在故障清除时间、最大有功功率等方面的仿真计算比较表明,以IEEE ST1A代表的静态励磁系统应被视为分布式发电新装(更换)的最佳选择,因为其抗动态干扰的性能优于直流和无刷励磁系统,在大多数情况下接近成本最高的复合系统。
静态励磁系统的维护成本低于本文中提出的所有研究类型的成本,不使用特殊变压器,并且设计难度低,可以在较高的电压限值下运行,在扰动期间达到理想的上限电压和电流。从应用性方面讲,静态励磁系统相对于其他励磁系统更具优势。
[1] 姚辉. 同步发电机励磁实时仿真测试系统研究[D]. 西安: 西安理工大学, 2005.
[2] 任小超, 刘丛洲. 阿海水电厂静态励磁系统的应用与设备选型分析[J]. 电气技术, 2015, 16(12): 157-159.
[3] 李阔. 自并励励磁系统灭磁原理与工程应用[J]. 电气技术, 2014, 15(7): 48-50.
[4] Artale G, Cataliotti A, Cosentino V, et al. Smart interface devices for distributed Generation in smart grids: the case of islanding[J]. IEEE Sensors Journal, 2017, 17(23): 7803-7811.
[5] Manassero G, Santo S D, Souto L. Heuristic method for fault location in distribution feeders with the presence of distributed Generation[J]. IEEE Transa- ctions on Smart Grid, 2017, 8(6): 2849-2858.
[6] Freitas W, Vieira J M, Morelato A, et al. Influence of excitation system control modes on the allowable penetration level of distributed synchronous generators[J]. IEEE Transactions on Energy Conversion, 2005, 20(2): 474-480.
[7] Delgado Saa J F, Çetin M. Discriminative methods for classification of asynchronous imaginary motor tasks from EEG data[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering : a Publication of the IEEE Engineering in Medicine and Biology Society, 2013, 21(5): 716-724.
[8] 郭培源. 同步电机励磁系统动态特性模型的研究[J]. 工业工程, 1993(2): 22-29.
[9] Gonzalez-Longatt F, Fortoul C. Review of distributed generation concept: attempt of unification[C]//Inter- national Conference on Renewable Energies and Power Quality (ICREPQ). España: 2005. 16-18.
[10] De Abreu L L. Dynamic performance of synchronous generators connected to electric power distribution systems[Z]. 2005.
[11] Oliveira M O, Paz MCR, Bretas A S, et al. Active power control of hydro-electric power unit auxiliary synchronous generator connected to distribution systems[C]//Power and Energy Society General Meeting. San Diego, CA, USA: 2012.
[12] 蒋忠玮, 李岩. 无刷励磁同步发电机系统数字仿真分析与计算[J]. 微特电机, 1995(1): 6-9.
[13] Price W. Load representation for dynamic performance analysis[J]. IEEE Transactions on Power Systems, 1993, 8(2): 472-482.
[14] Price W W, Taylor C W, Rogers G J, et al. Standard load models for power flow and dynamic performance simulation[J]. IEEE Transactions on Power Systems, 1995, 10(3): 1302-1313.
[15] 刘承榆, 刘维友. 同步发电机参数和试验的数字仿真[J]. 天津大学学报, 1994(1): 77-82.
Dynamic performance comparison of excitation system of distributed generation synchronous generator
Cao Yi Yang Xigang Liu Aijun
(Guodian Science and Technology Research Institute Co., Ltd, Nanjing 210023)
This paper mainly analysis the dynamic performance of several excitation systems of synchronous generator in distributed generation system. Through the use of related software simulation environment,/relationship changes, short-circuit reactance, fault clearing time, maximum active power and voltage curve of the system are simulated and its performance is under discussion. The results show that the static excitation system has better dynamic disturbance resistance and lower maintenance cost. The static excitation system has more advantages than other excitation systems in terms of applicability.
distributed generation; synchronous generator; excitation system; dynamic performance
2018-05-20
曹 沂(1962-),男,江苏人,高级工程师,主要从事发电厂设备管理和研究工作。
