某大跨度钢箱连续梁支撑体系仿真优化分析

周细辉，黄 坤

（南昌市城市规划设计研究总院，江西 南昌 330000）

0 引言

仿真分析是钢箱梁设计计算最为有效的途径[1-4]。但通过仿真分析准确把握钢箱梁的受力特性是建立在一定条件基础之上的，因此要求所建立的仿真分析模型必须能够充分反映所分析结构的力学行为本质并尽可能逼近其实际受力状态[5-6]。建立符合钢箱梁受力实际的仿真分析模型是采用数值分析方法进行钢箱梁力学特性研究的基础和基本前提。数值模型不可能和实际结构完全一致，这一过程不可避免地存在近似和简化。通过数值模型充分反映钢箱梁的力学行为本质并尽可能逼近结构的实际受力状态是仿真分析的关键和获取结构真实受力状况的基础。

本文以一座跨海钢箱连续梁大桥为研究对象，研究钢箱梁仿真分析模型边界条件的模拟方法，并辅以理论方法和钢箱梁实际工作状态对于所建立的模型及其分析结果进行对比分析，以期为今后大跨度钢箱连续梁支撑体系的仿真优化分析提供参考[7-9]。

1 工程概况

研究对象为某跨海大桥其中一联，此联采用110 m+150 m+110 m的变截面连续钢箱梁形式，材料均采Q345q。主梁采用带翼板钢箱梁，支点处梁高6.5 m，跨中等截面处梁高4.5 m，梁底高度变化为二次抛物线线型，等宽段的桥面宽33.1 m，桥型布置如图1、图2所示。梁段各板件厚度参数如表1所示。

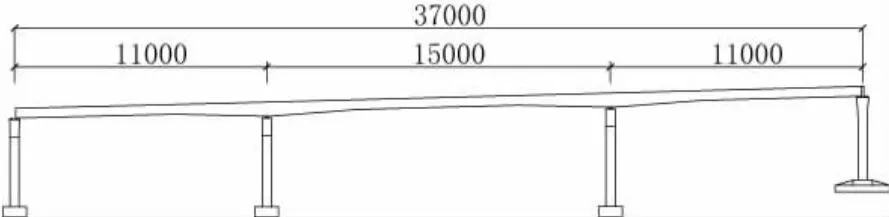
图1 桥型立面布置简图（单位：cm）

图2 钢箱梁标准断面（单位：mm）

表1 构件尺寸参数

2 有限元模型

2.1 箱梁有限元模型的建立

采用ANSYS14.0软件，建立了全桥的运营阶段分析模型。模型的板件尺寸、板件厚度等参数均严格按照设计图纸来模拟，有限元模型未考虑桥梁的纵坡和横坡。

有限元模型单元均采用shell63壳单元进行模拟。shell63单元是ANSYS的典型板壳单元，既具有弯曲能力，又具有膜力，可以承受平面内荷载和法向荷载，可以考虑材料应力钢化效应和结构大变形效应，适用于钢箱梁三维仿真分析。该模型建立了整个桥梁的1/2结构，全桥运营阶段模型共划分为809 979个单元，节点总数为847 251，如图3所示。

图3 有限元模型示意图

为了提高计算效率，对横隔板上人孔、管道等进行了简化，如图4所示。

图4 横隔板几何模型简化

2.2 箱梁有限元模型边界条件

运营阶段全桥模型的边界条件主要是支座约束，支座约束情况如图5所示。由于建立的是一半结构，故在对称面处施加沿顺桥向的对称约束。

图5 全桥运营模型支座约束情况（单位：mm）

2.3 箱梁有限元模型荷载工况

对于全桥运营模型，其所受荷载有梁体自重作用、二期恒载作用、车辆荷载作用、温度荷载作用、风荷载作用和支座沉降作用。其中：二期恒载的线集度为77 kN/m；支座沉降考虑桥梁的最不利效应，并根据工程经验取支座沉降量为15 mm，沉降的桥墩为0#、2#墩，沉降量均为15 mm。

3 箱梁有限元计算分析

3.1 有限元模型边界条件模拟方式

钢箱梁边界条件的模拟采用3种方式。

模拟方式A：未考虑支座刚度，未释放支座转动。按照设计约束体系对各个支座位置底板上的节点施加竖向、横桥向或顺桥向方向的约束。

模拟方式B：考虑支座刚度，未完全释放支座转动。据设计单位提供的支座刚度（如表2所列）对模型的支座约束条件进行了改善，改善的方式为：为支座底板上的所有节点添加单向竖向弹簧单元，弹簧单元的总刚度即为该处支座的刚度，然后将弹簧单元的另一个节点固结。

表2 各个支座竖向刚度表

模拟方式C：考虑支座刚度，完全释放支座转动。为支座底板上的所有节点添加单向竖向弹簧单元，但竖向弹簧单元的另一个节点与底板下方一主节点耦合，主节点上再设置单向竖向弹簧单元，从而完成转角的完全释放。

3.2 计算结果对比分析

分别对恒载工况下钢箱梁关键部位特别是支座处主要板件的应力进行分析对比，如图6、图7所示。

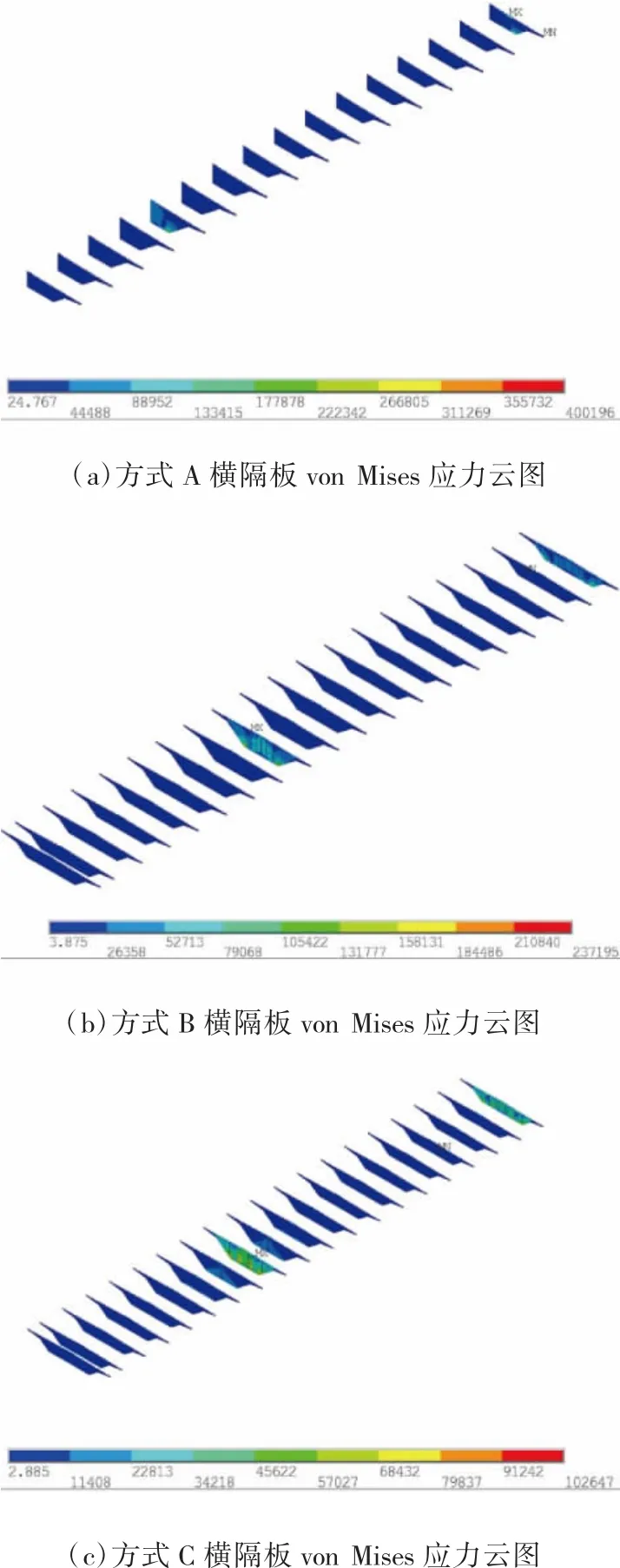
图6 横隔板von Mises应力云图（单位：kPa）

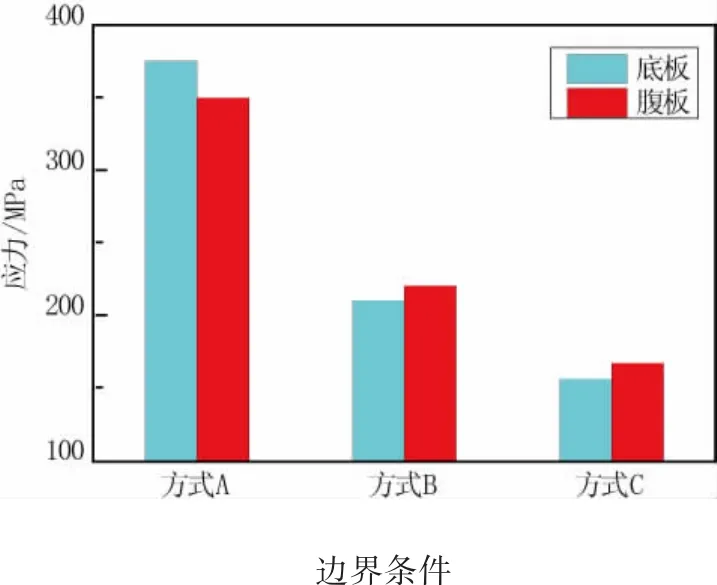
图7 不同边界条件模拟方式下的板件最大应力

在恒载工况下钢箱连续梁竖向挠度（下挠）计算结果如表3所示。

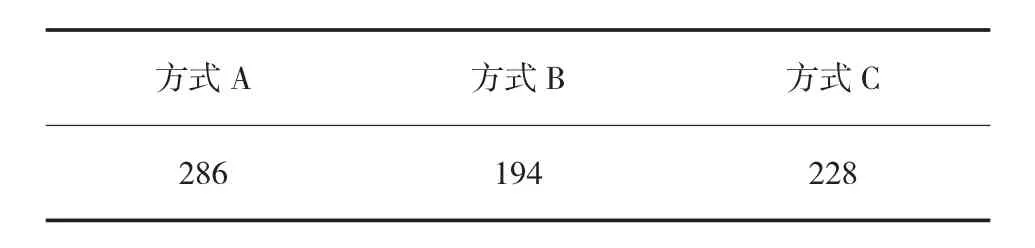
表3 不同边界条件模拟方式下的主梁最大挠度 mm

从计算结果来看，以方式A模拟钢箱梁边界条件底板的高应力区域主要集中在中跨支座附近。恒载工况下计算结果为：底板处最大Mises应力达到376 MPa，实腹式横隔板最大Mises应力为400 MPa，中腹板最大Mises应力为345 MPa。结合已建成的钢箱梁桥工程实例分析，这显然无法准确模拟支座的实际约束情况，局部存在较大的计算失真。原因主要是此方式支座上底板上全部节点的相应平动自由度被限制，相应梁体的转动自由度也被限制住，从而造成此处梁体无法转动，故造成此处的高应力。

与方式A相比，以方式B模拟钢箱梁边界条件的模型计算结果得到了较大改善。仍以恒载工况为例：底板处最大Mises应力为180 MPa，实腹式横隔板最大Mises应力为237 MPa，中腹板最大Mises应力为192 MPa。显然，与方式A计算结果相比，其应力情况得到了很大改善，改善的主要原因在于设置了支座竖向刚度之后，在外力作用下，支座上各节点可以产生不同位移，从而体现出支座的转动释放。但进一步分析发现，其应力值仍然偏大，如其中实腹式横隔板的最大Mises应力为237 MPa，经过对模型应力云图的分析研究后发现在中跨支座处底板的应力并不连续，主要是由于其转角并未完全释放，所以应力值仍然偏大。

以方式C模拟钢箱梁边界条件，底板处最大Mises应力为116 MPa，实腹式横隔板最大Mises应力为103 MPa，中腹板最大Mises应力为130 MPa。该结果相对于方式A、方式B的计算结果大为改善，且结合钢箱梁历史设计经验可知，用方式C来模拟钢箱梁边界条件能够更为准确地模拟结构的实际受力状态。

4 结论

（1）在相同工况作用下，不同边界条件模拟方式的钢箱连续梁有限元模型计算结果存在显著差异。边界条件模拟方式的选择在钢箱连续梁有限元仿真分析中应结合历史设计经验和理论分析慎重选择。

（2）在钢箱连续梁的仿真分析中，考虑支座刚度、完全释放支座转动是十分必要的，它能够更为准确地模拟钢箱梁支座体系处结构的实际受力状态。