基于最优权阈值ELM算法的锂离子电池RUL预测

刘 柱 ，姜媛媛 ,2，罗 慧 ，周利华

（1.安徽理工大学电气信息与工程学院，淮南 232001；2.南京航空航天大学自动化学院，南京 210016；3.南京农业大学工学院，南京 210031）

锂离子电池是一种具有比能量大、自放电率低、安全性能好、循环寿命长等优点的绿色充电电池，因而被广泛用于消费数码类、动力安防类、医疗保健类和航空航天等领域[1-4]。锂离子电池良好的工作状态既可以保证仪器设备的正常使用，也可以避免严重的故障事故。锂离子电池剩余寿命RUL（remaining useful life）的预测作为农业技术领域的关键技术之一，目前已经成为国内外的研究热点。

目前国内外主流的锂离子电池RUL预测方法是基于数据驱动的方法，其利用锂离子电池寿命特征参数，借助算法模型，如贝叶斯推理概率[5]、支持向量机[6]、高斯过程回归[7]、回声状态网络[8]、极限学习机[17]等，进行分析与预测，以得到电池寿命参数趋势和退化程度等信息。极限学习机ELM（extreme learning machine）具有训练速度快、预测精度高和参数设置简单等优点，被广泛用于电力价格预测[9]、风力发电预测[10]、工业指标参数预测[11]等方面。ELM用于预测时，由于其输入层与隐含层间的权值以及隐含层阈值的随机选取，导致每次的训练结果不同，并存在细微偏差，进而影响模型的预测精度，因此可寻求最优的ELM权阈值以获取最好的预测效果。文献[12]基于遗传算法GA（genetic algorithm）优化ELM的权阈值，但GA寻优过程中容易陷入局部最优，致使预测精度也呈现局部最好而非全局最好。蚁群算法ACO（ant colony optimization）是一种具有正反馈机制的模拟进化算法，能够较大概率地发现最优解且搜索过程不易陷入局部最优，但蚁群算法需要较长的搜索时间，不适用于在线搜索。

为此，本文充分利用遗传算法的快速性、随机性、收敛性与蚂蚁算法的并行性、正反馈性、求解精度高等特点，融合GA和ACO两种算法，构造基于遗传蚂蚁算法GAAA（genetic algorithm ant algorithm）的最优权阈值ELM锂离子电池性能预测模型，基于间接参数（等压降放电时间）和直接参数（实际容量）的两种预测方法，最终实现锂离子电池剩余寿命的快速准确预测。

1 最优权阈值ELM预测方法

1.1 极限学习机

极限学习机ELM是Huang等[13]提出的单隐层前馈神经网络SLFN（singlehidden layer feedforward neutral network），其机理简单描述如下。

首先给出m个输入变量，M个隐含神经元，n个输出隐含层神经元。ELM的数学表达式为

式中：g为激活函数，取Sigmoid函数；Win为输入权值；ω为输出权值；b为隐含层偏差值；N为样本总数；uk为m维输入变量；vk为输出变量。

设有 N 个样本对为（ui，Ii），1≤i≤N。训练时，输入权值Win和偏差值b随机初始化并保持不变，只要确定隐含层神经元个数及隐含层激活函数，即可计算出输出权值ω，具体算法为

式中：H+为隐含层输入矩阵 H的摩尔-彭洛斯（Moore-Penrose）广义逆矩阵[14]；I为期望输出矩阵，I=（I1，I2，…，IN）T。将 H 展开为

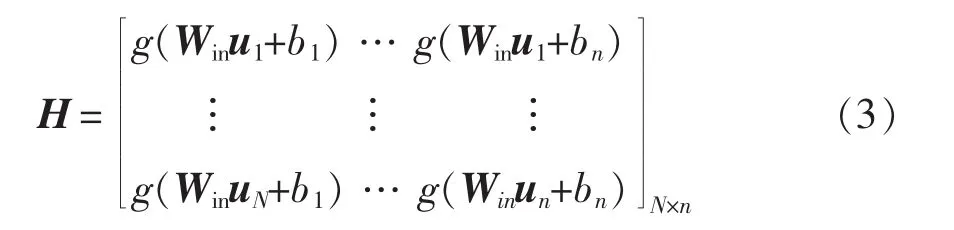
相比于传统的梯度下降理论算法，极限学习机学习速度更快，具有更好的泛化性能，应用于锂离子电池RUL预测能够极大地提高预测的速度与准确性，尤其在输入权值Win和隐含层偏差值b最优时预测精度最佳。

1.2 基于GAAA的最优权阈值ELM预测

GA是以生物进化方式编制的全局搜索算法[15]，其只需进行选择、杂交、变异3种遗传运算就可寻出最优解，具有快速性、随机性和收敛性等优点。ACO是一种基于种群寻优的启发式搜索算法[16]，通过对不同种群间的信息素识别选择合适的搜寻路径，具有并行性、正反馈性、求精解效率高等优点。GAAA采用GA初步寻优，生成初始信息素分布，再利用ACO深度寻优，使两种算法优劣互补，在求解效率上优于GA，在时间效率上优于ACO。

ELM具有良好的训练速度和泛化性能，由于ELM固有的权阈值随机性会影响其泛化性能和预测精度，故采用GAAA优化ELM的权值与阈值。其实现流程如图1所示。

具体实现步骤可分为以下4个阶段。

（1）数据预处理。先将数据集划分为训练样本与测试样本，再将训练样本划分为训练样本输入与训练样本输出，对训练样本输入编码，产生初始种群。

图1 GAAA融合算法对ELM寻优流程Fig.1 Flow chart of ELM optimization using GAAA fusion algorithm

（2）遗传算法。定义适应度函数，生成初始种群，对于得到的群体进行选择、复制、交叉、变异操作，生成下一代种群，辨别算法终止条件；算法终止后，得到权阈值的初始信息素分布，进入蚁群算法。

遗传算法中，以ELM训练集预测平均误差作为其适应度函数，即

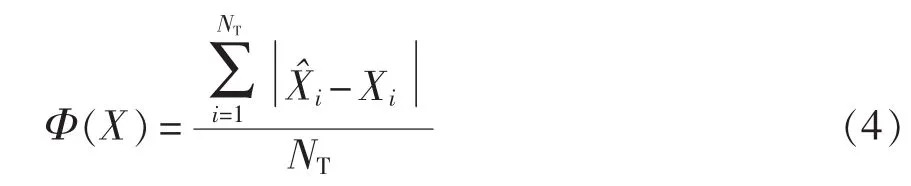
（3）蚁群算法。适应度函数的选择与遗传算法相同，设置初始信息素λ和蚂蚁数量N0，辨别算法是否终止。若满足，则算法终止；若不满足，则信息素挥发，继续寻优。算法终止后，得出最优权值与阈值，用于ELM预测。

蚁群算法中，适应度函数的选取与遗传算法相同；初始信息素λo设置由GA优化解得出；经过s个时间段，蚂蚁完成1次循环，信息素的更新方程为

（4）ELM预测。由步骤（3）获取ELM预测模型，将测试样本输入ELM预测模型，得出结果。

2 实验结果与分析

2.1 实验数据的获取

本文对NASA PCoE研究中心测试的锂离子电池数据集进行RUL预测。采用型号为18650、容量为2 A·h的市售锂离子电池，实验分为多组进行，测试温度为25℃。测试方式为：先以1.5 A恒流充电，电压达到4.2 V后，再以2.0 A恒流放电至2.5 V；如此循环进行，测量监测数据。本文以第3组5号电池实验数据作为ELM预测模型验证实例，以锂离子电池额定容量的70%作为失效阈值[7]，失效阈值为1.38 Ah。

2.2 间接寿命特征参数

锂离子电池寿命特征参数分为直接参数（实际容量）与间接参数（电压、电流、阻抗等）。实际应用中，常用传感器难以检测锂离子电池内部机理状态，直接参数的获取一般通过安时法估算得出，对于有限数据，采用直接预测方法会因为缺少历史数据导致预测建模模型不准确。因此，本文离线监测采用直接预测方法，而在线监测采用间接预测方法。本文选用等压降放电时间作为锂离子电池间接寿命特征参数，即温度恒定时，锂离子电池从一高电位恒流放电到一低电位所用的时间即为等压降放电时间，数学表达式为

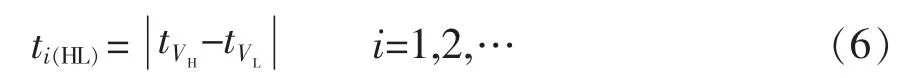
式中：ti（HL）为第 i个循环寿命周期下等压降放电时间差；为高电压时所对应的时间；为低电压时所对应的时间。

等压降放电时间与实际容量如图2所示。通过一阶偏相关系数法[17]确定等压降放电时间序列与实际容量序列之间的相关性，基于NASA的锂离子电池数据得出相关系数为0.784 4，为强相关性，表明间接寿命特征参数可以表征锂离子电池的健康状况，能够用于锂离子电池RUL预测。因此，基于锂离子电池特征参数时间序列，构建最优权阈值ELM预测模型，预测出锂离子电池未来时刻的特征参数，以评估其RUL。

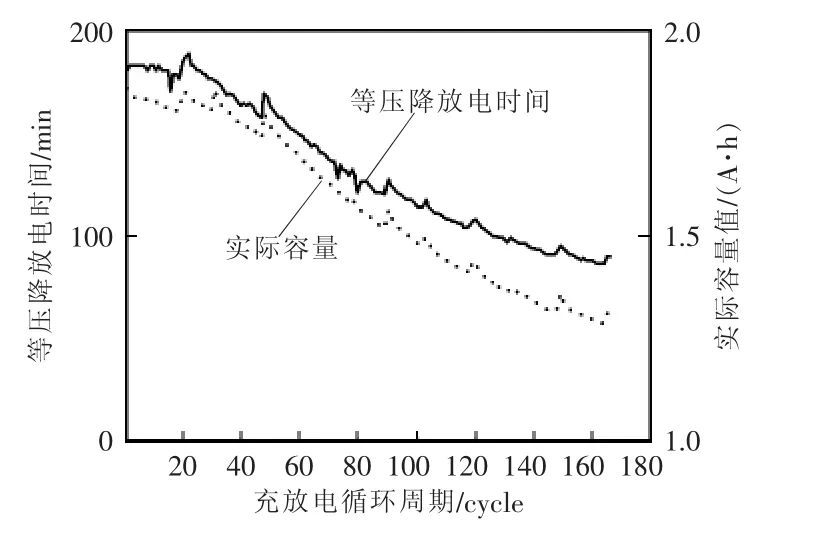
图2 等压降放电时间与实际容量Fig.2 Time interval to equal discharging voltage and the actual capacity

2.3 等压降放电时间预测实际容量的GAAA-ELM模型

选取放电阶段为tVH（对应高电压为3.8 V）至tVL（对应低电压为3.5 V），以等压降放电时间Ti作为模型输入，实际容量Qi作为模型输出。其中，B5中共有168组等压降放电时间和实际容量数据，取前100组作为训练集，后68组作为测试集，运行GAAA优化ELM神经网络模型。根据实测，相关参数设置如表1所示，模型预测结果如图3所示。

由图3可知，此时预测实际容量失效阈值Qf所对应的等压降时间失效阈值Tf即为间接寿命特征参数的预测失效阈值。

2.4 等压降放电时间的GAAA-ELM预测模型

构建等压降放电时间预测的GAAA-ELM神经网络模型，以B5中168组等压降放电时间的前100组作为训练集，后68组作为测试集，参数设置与等压降放电时间与实际容量的关系模型相同，实现的等压降放电时间迭代预测，等压降放电时间失效阈值Tf已由图3结果求出，预测结果如图4所示。

表1 GAAA优化ELM神经网络参数设置Tab.1 Parameter setting of ELM neural network using GAAA optimization

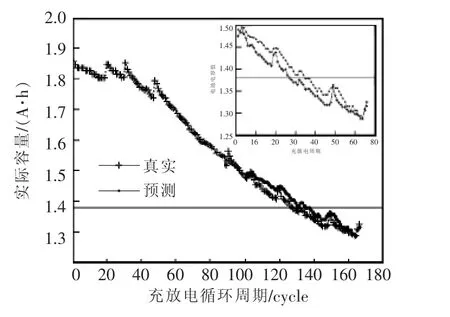
图3 真实实际容量与GAAA-ELM模型预测的容量Fig.3 The true actual capacity and the capacity predicted using GAAA-ELM model

2.5 等压降放电时间预测锂离子电池RUL实验结果分析

利用等压降放电时间作为寿命特征参数，将本文提出的GAAA-ELM预测模型与传统BP（back propagation）神经网络（BP神经网络采用与ELM神经网络相同的节点数与激活函数）、ELM及GA-ELM预测模型相比较，结果如表2所示。

图4 基于GAAA-ELM预测模型的等压降放电时间预测结果Fig.4 Prediction result of the time interval to equal discharging voltage based on GAAA-ELM prediction model

表2中，RULerror为锂离子电池剩余寿命预测误差，MAPE为预测结果平均相对误差，时间为预测所花费时间，则有

式中：RULpr为剩余寿命预测值；RULtr为剩余寿命真实值。

式中，Nl为测试次数。

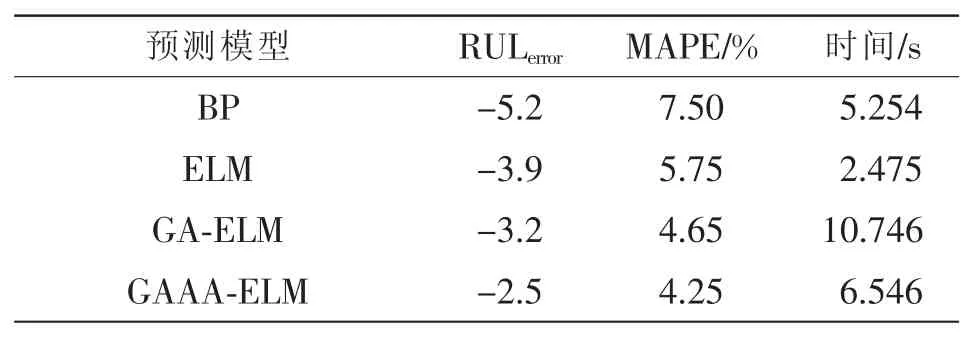
表2 基于等压降放电时间的4种锂离子电池RUL预测模型性能对比Tab.2 Performance comparison among four kinds of lithium-ion battery RUL prediction models based on pressure drop discharge time

由表2可知：ELM预测方法在预测时间和精度上面都明显优于传统BP方法，训练效率得到了提升；GAAA-ELM预测方法在时间和精度上都优于GA-ELM预测方法，并且相对于ELM预测方法具有更好的预测精度，具有良好的实用价值。

2.6 实际容量预测锂电池RUL实验结果分析

利用容量作为寿命特征参数，将本文提出的GAAA-ELM预测模型与传统BP神经网络、ELM及GA-ELM预测模型相比较，4种预测模型参数设置与利用等压降放电时间参数设置相同，结果如表3所示。

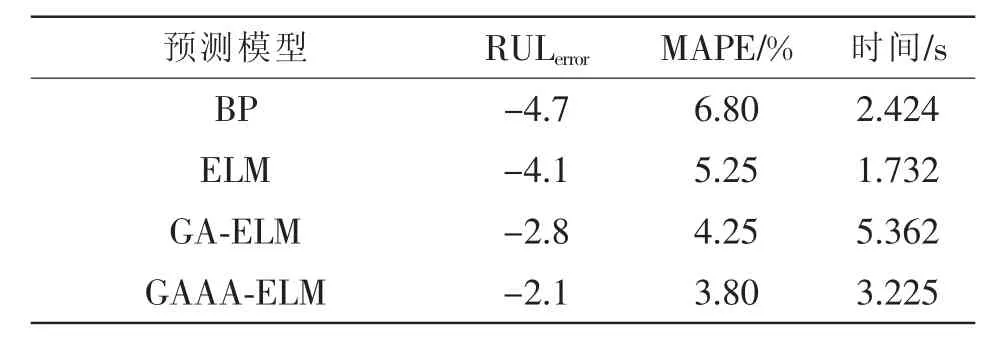
表3 基于实际容量值的4种锂离子电池RUL预测模型性能对比Tab.3 Performance comparison among four kinds of lithium-ion battery RUL prediction models based on real capacity

由表3可知，ELM的学习速度比BP神经网络快的多，而ELM参数设置比BP神经网络更少。优化后的ELM神经网络具有更高的训练精度，符合锂离子电池RUL的实际预测。

3 结语

本文通过对等压降放电时间与实际容量进行锂离子电池RUL预测，给出了基于GAAA优化ELM最优权阈值的方法体系。采用NASA公开的锂离子电池数据集测试验证了GAAA-ELM方法具有良好的RUL预测能力，符合数据测量方便、算法简单、处理速度快、结果准确等优点；并与传统的BP方法、ELM预测方法和GA-ELM预测方法相比较，其结果表明本文所提出的GAAA-ELM预测方法具有更好的实用性与更高的预测精度。