基于单相H桥级联变换器的高斯模糊算法电压平滑调制策略
2018-08-17韩鹏程何晓琼
韩鹏程,何晓琼
(西南交通大学电气工程学院,成都610031)
多电平变换器近年来在高压大功率的场合得到了广泛的应用[1-3]。级联型变换器由于其模块化、可扩展性以及简单的布局,其拓扑结构近年来得到了广泛的研究[4-5]。级联变换器的一种拓扑结构是基于H桥级联的整流器CHBR(cascaded H-bridge rectifier),它可以将高压交流电转换为低压直流电,并且被应用于电力电子变压器PETT(power electronic traction transformer)和固态变压器 SST(solid state transformer),从而取代传统的变压器[4-6]。但是一旦各模块输入功率或者输出功率不相等,CHBR各模块直流侧电容电压将会不均衡。
为了保证直流侧电容电压的均衡,很多的方法在工业界和学术界被提出[4-20]。文献[4]将电力电子变压器的整流侧通过直直变换器将CHBR的输出电压隔离,然后把每个单元并联实现所有模块输出相等。但是,PET仍然通过使用PI控制器保持电压的均衡。如果上述结构中没有将输出电压并联,就必须需要通过加入控制策略,保证当模块输出功率不平衡时输出电压的平衡。文献[8]中分别讨论了3种以PI控制器为基础的CHBR电压均衡策略,并通过理论分析与仿真找到了其中正确的控制策略;文献[9]分析并验证了PI控制电压均衡的限制问题,尤其是在文献[10]中,一种新型的模块化级联多电平变换器也被应用于电压均衡,这种转换器有着使用PI控制器的多绕组高频变压器。上述文献都阐述了PI控制器如何改变每个模块输入输出功率来控制直流侧电压的均衡,该方法具有较好的鲁棒性,并且在工业中得到了广泛的应用。
基于上述文献的研究,本文提出了一种模糊调制策略,用于CHBR直流侧电压的均衡,能够保证每个模块开关器件的平稳变化。由于这种调制策略是通过计算得出开关状态的脉冲序列,因此可以适用于N模块。实验结果表明,当CHBR的一个负载被去除时仍然可以保证直流侧电压的均衡。
1 系统结构
1.1 拓扑结构和控制算法
图1(a)所示为CHBR的拓扑结构,级联H桥变换器将网侧电压Us从交流转换成直流Vdc。CHBR的数学描述为

式中:Ls为整流器的滤波电感;is为网侧电流;Un为CHBR的输入电压;ui为H桥的输入电压;W为网侧角频率。
CHBR的控制算法过程示意如图1(b)所示。整流器采用瞬态电流控制策略,当取得瞬态电流控制计算结果,该电压将会通过载波层叠调制计算;然后通过高斯模糊函数对直流侧电压进行模块化排序;最后由序列脉冲发生器确定了每个模块的开关状态。
瞬态电流控制是为了保持电网电流正弦化和功率因数统一从而得出直流侧参考电压的总和,它是由电压外环和电流内环组成的。如图1(b)所示,直流母线参考电压之和与每个模块直流母线电压 Vdci(i=1,2,…,n)的误差通过 PI调节器后获得网侧参考电流。
相位和频率可以通过锁相环PLL(phase-locked loop)检测,并且被用作的相位和频率。电网电流is可以通过比例控制器跟踪,从而保证is为正弦波。因此系统能够获得参考电压uref,表示为
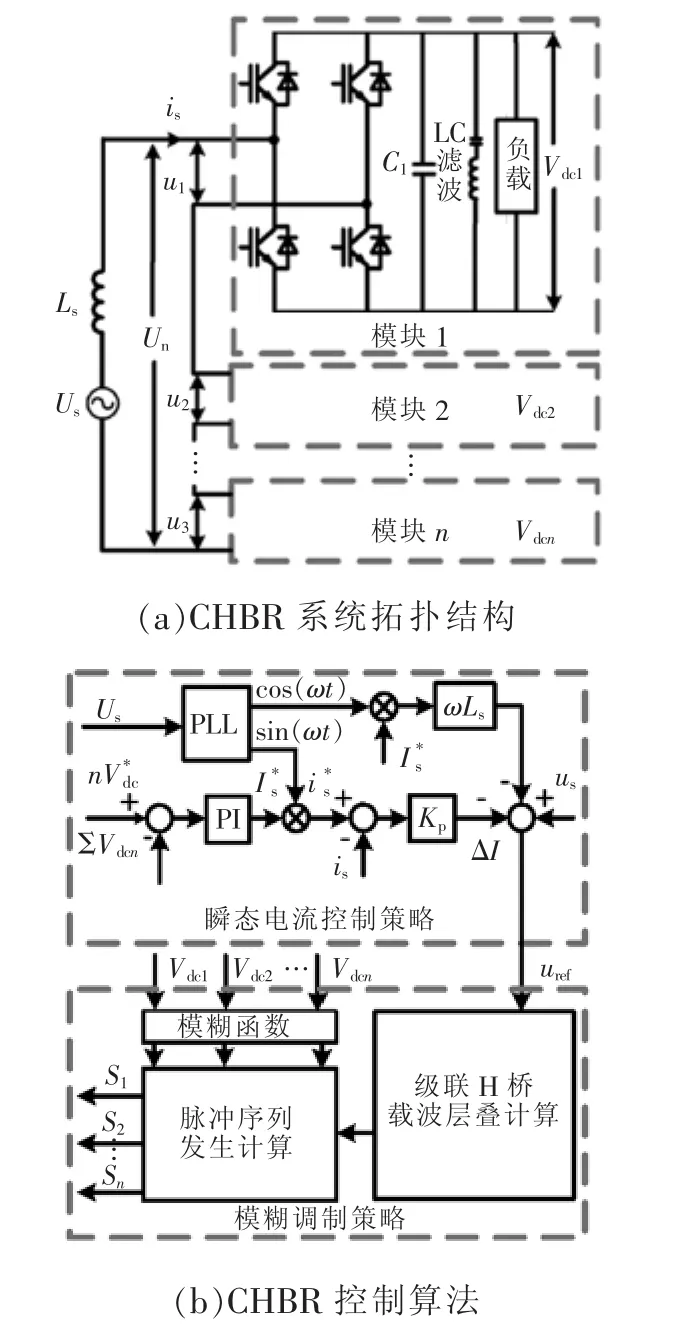
图1 CHBR系统拓扑结构与控制算法Fig.1 System topology configuration and control algorithm for CHBR
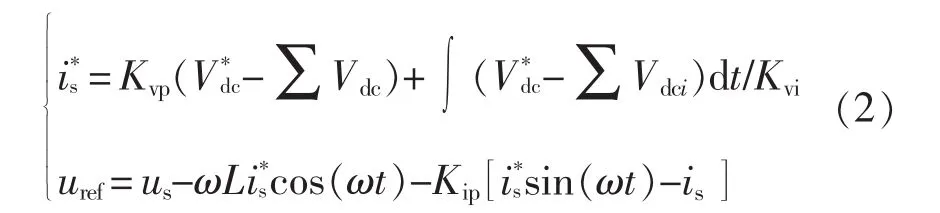
1.2 CRHB拓扑结构分析
为了清楚地阐述载波层叠调制计算、模糊算法调制,本节给出了CHBR分析。通过基尔霍夫电压定律 KVL(Kirchhoff’s voltage law),CHBR 的 Un可以表示为

式中:n为模块的数量;Si为模块i的开关状态。
图2为一个模块的开关状态。根据H桥的不同IGBT的状态,Si的3种结果可以表示为

其中IGBT状态展示了功率半导体S1~S4的状态。把IGBT视为一种理想开关,1代表开通,0代表关断。因此,忽略每个模块Vdc之间的偏差,对于任意一组满足式(3)的开关状态序列,可以将Un由CHBR的直流电压以及开关状态表示。
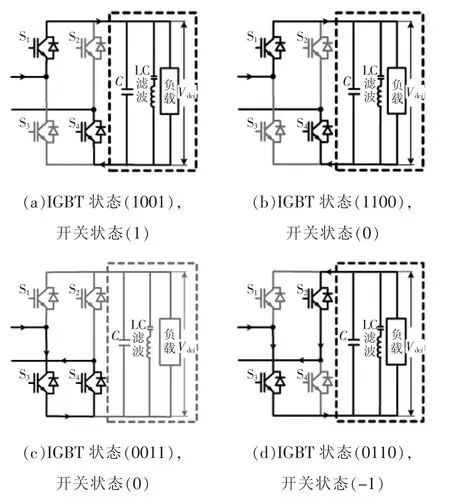
图2 H桥开关状态Fig.2 Switching states of H-bridge
根据H桥模块开关状态,则模块输入功率为

式中,Pi为模块输入功率。当直流环节电压为正时,功率流动是否为正取决于开关状态Si和电流is。基于能量守恒,模块的输出功率为

Pout的可能出现的状态有:
(1)当Si和is同为正或者同为负时,Pout为正。根据式(6),模块从电网吸收功率并且Vdci上升。
(2)当 Si或 is为 0 时,Pout为 0。模块不从网侧吸收功率。根据式(6),Vdci或许会下降。但当模块空载时,Vdci仍然不变。
(3)当Si和is相反时,Pout为负。模块向网侧发出功率,根据式(6),Vdci会下降。
2 模糊算法调制
2.1 载波层叠的计算
本文以4模块H桥级联整流器为例分析模糊算法调制策略。基于载波层叠调制,载波层叠调制计算的结果。如图3所示,调制的电平由CHBR模块的数量决定,载波层叠调制计算的输出被认为是Si总和的参考。
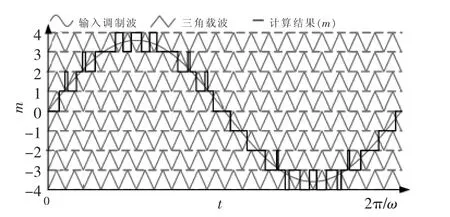
图3 CHBR载波层叠计算Fig.3 Carrier stacked calculation of CHBR
表1所示为传统H桥级联整流器输出开关状态。可以看出,状态在开关发生变化时会产生跳变。为了解决这个问题,首先根据H桥电容电压大小进行排序用以决定各H桥输出的波形,从而控制各H桥电容电压的充放电,平衡各桥的直流侧电容电压。此方法不用独立控制每个桥直流侧电容电压,通过比较交换的方式使得控制方法变得简单。但是为了均衡各模块电容电压,每个模块的输出电平会发生跳变。根据CHBR拓扑结构分析以及开关状态特性,可得到开关状态的排序如表2所示。
表2说明了当Si改变一次时IGBT的动作个数。由表可知,当从1跳变至0或从0跳变至-1或1时,开关变化2次,当从1直接跳变至-1时,开关变化4次,因此,在同一开关周期内,开关状态在1和-1之间变化个数最多。
为了给每个模块选择最合适的开关状态,特分析开关状态特性如下:
(1)Si=1。如果 is>0,则 Pi为正;如果 is<0,则 Pi为负。该状态能够改变Vdci,有利于平衡直流侧电压。
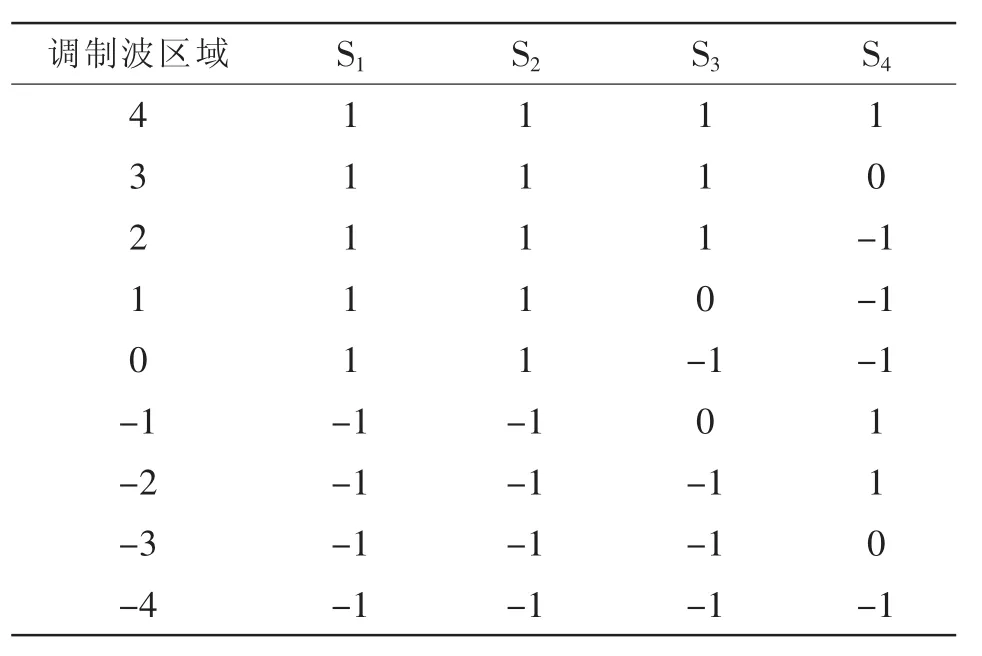
表1 传统H桥级联整流输出开关状态Tab.1 Switching states of the traditional cascaded H-bridge rectifier output
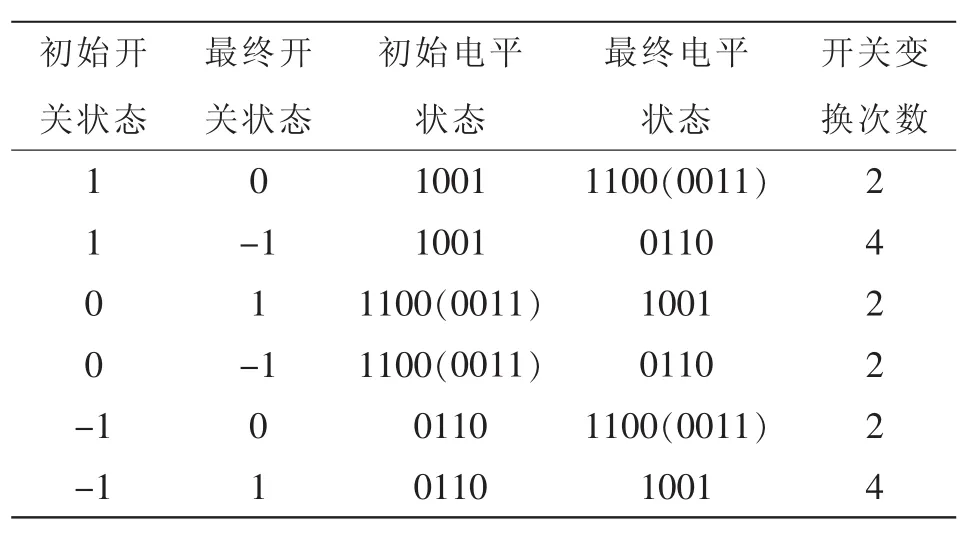
表2 电压等级和开关信号Tab.2 Voltage levels and switching signals
(2)Si=0。无论 is为何值,Pi为 0,这不利于平衡直流侧电压。但是,0状态是必要的,因为该状态能够通过保护开关状态,防止从1跳变到-1,从而实现平滑调制。
(3)Si=-1。如果 is>0,则 Pi为负;如果 is<0,则 Pi为正。该状态能够改变Vdci,有利于平衡直流侧电压。
2.2 基于高斯模糊算法的电压平滑调制
高斯模糊是一种基于高斯函数的二维图像处理技术,是为了避免图像颜色交错部分锐化的一种技术手段,其原理为
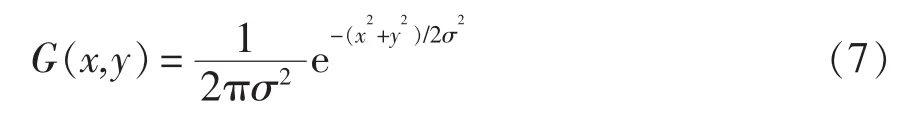
式中:G(x,y)为二维空间向量;x、y 分别为二维空间坐标。将二维高斯函数化简为一维高斯函数,有
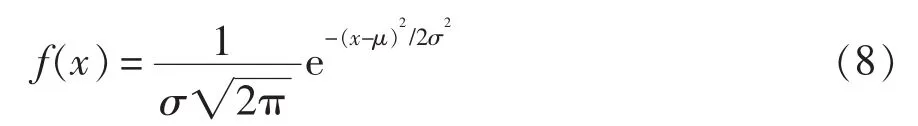
由于级联整流模块的输出状态为 1、0、-1,因此只有当状态从1到-1或者从-1到1时会发生矢量跳变,则根据上述公式可以推广到级联整流器的开关状态产生,即
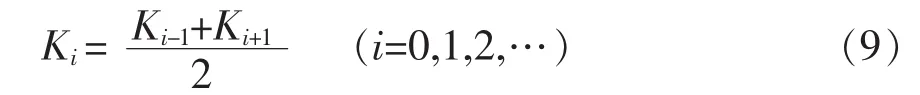
式中:Ki为每个开关周期需要的输出状态;Ki-1为上一开关周期的输出状态;Ki+1为下一开关周期的输出状态。又每个模块的开关状态均为从1开始,-1结束,因此可补充K0=1,Kn+1=-1。根据上述推导,模糊算法的调制波产生模式如下:
(1)等待触发。为了使开关状态平滑改变,仅当KiKi+1≠0,即KiKi+1+1=0时,调制函数才会作用。在此步骤中,flag将会重新置为0。
(2)触发。当 KiKi+1+1=0 时,将 KSi-1寄存到调制函数中,则有 Ki=(Ki-1+Ki+1)/2,交换 rank,其 flag 将会变为1;否则,其flag仍为0。
高斯模糊算法平滑调制流程如图4所示,则根据上述函数产生的调制波如表3所示。
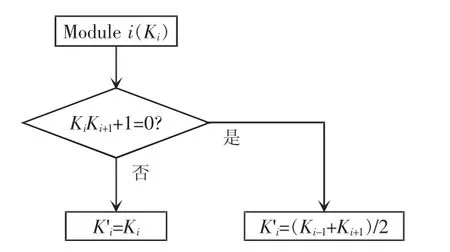
图4 高斯模糊算法平滑调制流程Fig.4 Flow chart of smooth modulation with Gaussian blur algorithm
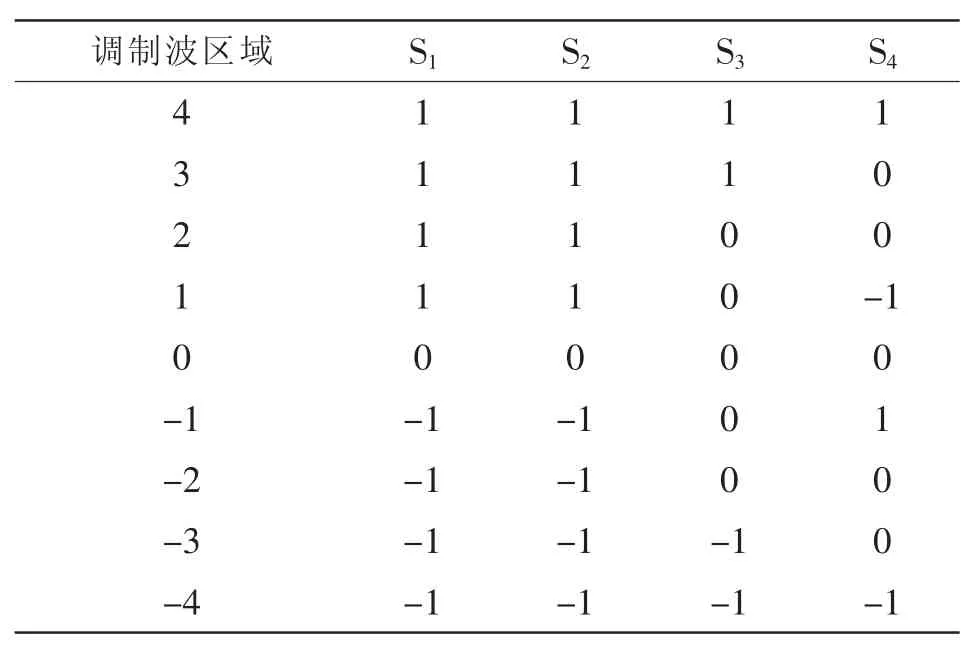
表3 基于模糊算法的电压平滑调制输出开关状态Tab.3 Switching states of the smooth voltage modulation output based on blur algorithm
3 实验验证
为了验证模糊算法电压平滑调制的正确性,本文搭建了4模块H桥级联变换器,如图5所示。系统的输入电压是工频100 V,输出电压是38~60 V。本文控制器选择EP3C55F484C8型的FPGA,实验具体参数如表4所示。

图5 实验模型平台Fig.5 Experimental model platform
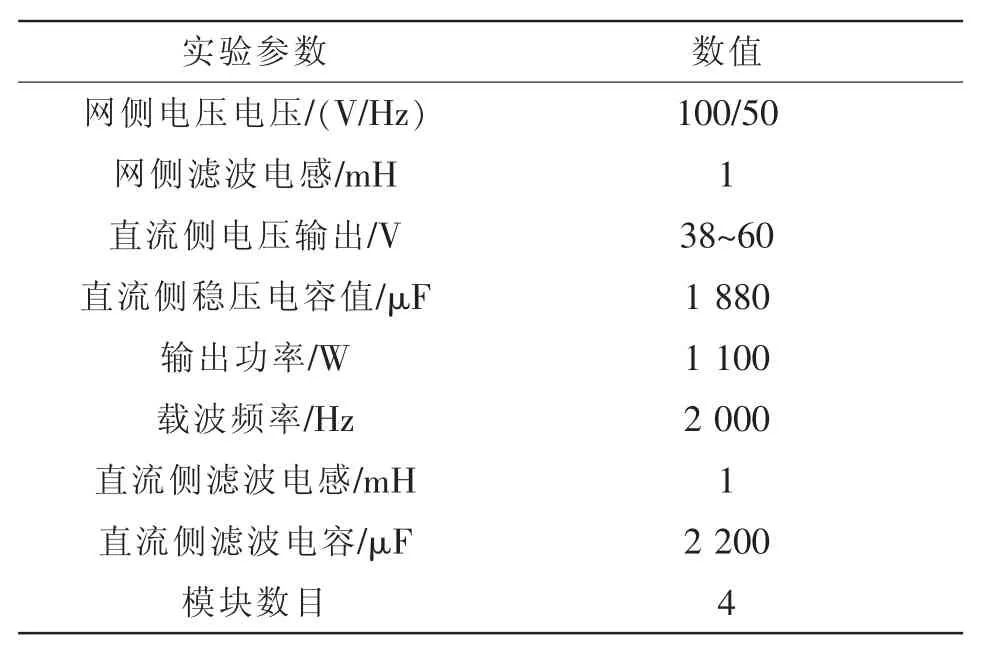
表4 实验参数Tab.4 Experimental parameters
图6(a)所示为常规排序调制策略下4模块输出电压波形与网侧级联波形。由图可知,4模块为了保证模块间均压,因此会产生电平跳变。当4模块的直流侧电压 Vdc1<Vdc2<Vdc3<Vdc4时负载不平衡对模块的开关状态产生影响,此时等效频率大于给定载波频率2 000 Hz。当负载平衡时,频率会自动均衡每个模块的输入功率。图6(b)所示为CHBR输入电压,可由载波层叠调制计算出来,每个模块的输入电压合成之后来作为PDC的参考电压,并且展示了当负载不均衡条件下模糊调制策略下电压没有跳变的波形。图6波形中,模糊调制策略下输入电压改变是平滑的。
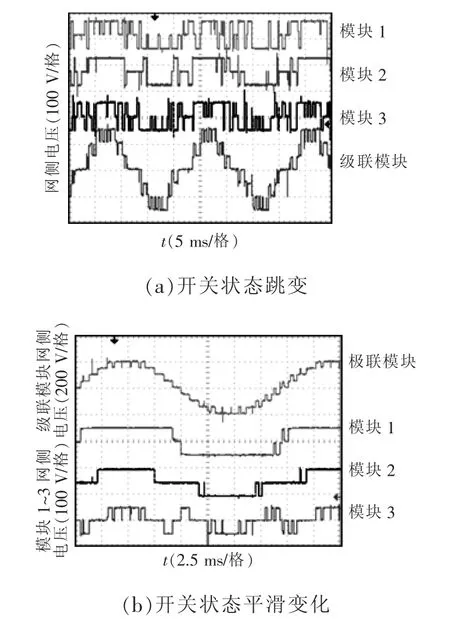
图6 开关状态跳变与平滑变化实验波形Fig.6 Experimental waveforms of jumps and smooth changes of switching states
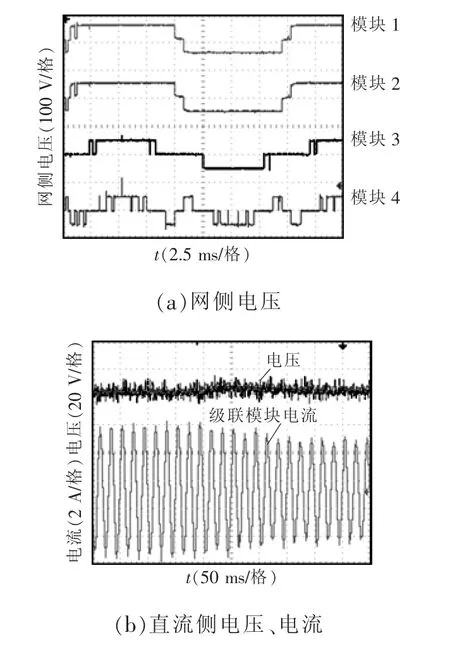
图7 网侧电压与直流侧电压电流波形Fig.7 Waveforms of grid-side voltage and DC-side voltage and current
模糊算法电压平滑调制工作下,网侧电压和直流侧电压电流波形如图7所示。当调制度M=0.83时,4个模块中的一个模块的负载被移除,此时Δy=0,每个模块的直流侧电压可以保持均衡,如图7(a)所示。如图7(b)所示,当模块1负载被移除之后,网侧电流下降到没有移除之前电流的3/4,每个模块的直流侧电压均保持稳定。
如图8所示为图7实验波形负载均衡和不均衡时的THD测量参数。由于CHBR会减小THD,因此网侧电流会在负载均衡时保持正弦化。由于每个模块的开关状态由于模糊算法电压平滑调制被重新分配,因此CHBR每个模块的直流侧电压Un在模糊调制策略下保持不变。

图8 负载均衡和负载突变网侧电流THDFig.8 THD of grid-side current when the load is balanced or changes suddenly
4 结论
本文通过分析CHBR级联拓扑在整流工作时的工作状态,研究了电压均衡策略调制的原理。基于模糊调制策略原理,本文提出了有关电压不均衡度的计算,并且通过实验对模糊调制策略进行了验证。基于CHBR级联拓扑结构的模糊调制策略的研究结论如下。
(1)当开关状态在1和-1之间跳变时,CHBR的开关频率变高。
(2)当1个负载被移除时,模糊调制策略依然可以保证4模块CHBR的直流侧电容电压均衡。
(3)在模糊调制策略下开关状态平滑变化。
