高压隧洞裂隙渗流的离散元数值分析

林太清，高江林

(江西省水利科学研究院，江西南昌330029)

0 引 言

引水式电站与抽水蓄能电站输水隧洞呈现大埋深、长距离的特点。受隧洞围岩裂隙发育的影响，防渗措施往往必不可少，也对隧洞的安全运行起到了至关重要作用。固结灌浆是一种常用的处理措施，针对其渗流控制效应的分析，对工程设计的优化、工程运行安全的保障和工程投资的合理利用具有重要的现实意义。裂隙岩体的渗控分析方法有连续介质法[1]、离散裂隙网络法和双重介质法[2]。Cundall于1971年提出的一种基于非连续介质力学的数值计算方法[3]，即离散单元法，认为岩体是岩块和岩块间的不连续接触面组合体。二维离散元程序(UDEC)是ITASCA公司基于离散单元法开发的二维离散元程序，Min KB等[4- 8]学者运用UDEC在裂隙岩体渗流问题的研究和实际工程的应用上取得了很好的效果。

本文基于离散单元法，采用二维离散元程序(UDEC)，对高压隧洞裂隙岩体的渗控效应进行了数值模拟分析，得到了高压隧洞裂隙岩体的优势渗透路径和渗控效应规律，可为渗控措施优化设计提供参考。

1 裂隙渗流分析的离散单元法

1.1 基本原理

离散单元法将所研究的岩体假定为离散块体的集合体，而节理、裂隙、断层等结构面被当作是这些离散体之间相互作用的接触面。块体之间相互作用力可以根据力和位移的关系求出。假定块体之间的法向力Fn正比于它们之间的法向“叠合”量，即

Fn=KnUn

(1)

式中，Kn为法向刚度系数；Un为位移的法向“叠合”量，这里所谓法向“叠合”量是计算时引入的1个假定的量，将它乘上1个比例系数，即接触法向刚度后，作为在计算中法向力的度量。

由于块体所受的剪切力与块体运动和加载的历史或途径有关，对于剪切力要用增量ΔFs来表示。设2个块体之间的相对位移为ΔUs，即

ΔFs=KsΔUs

(2)

式中，Ks为接触剪切刚度系数。

以上所示的力与位移关系均为弹性情况。对于塑性剪切破坏情况，按照摩尔-库仑准则计算。

单个块体的运动根据该块体所受的不平衡力和不平衡力矩的大小，按牛顿运动定律确定，即

采用中心差分法，可将式(3)左边改写为

将式(4)代入式(3)可得

利用Δt/2时刻的速度，可求解出Δt时刻的位移，即

之后，利用力-位移关系，可由位移求解出力。

对于承受外力荷载及重力作用的二维块体，可按下式计算其速度，即

从式(4)中得到速度后，可按下式求得块体的坐标位置，即

式中，θ为块体转角；xi为块体质心坐标。

综上所述，在每1个时步中计算出块体新位置，而后得到接触力。利用合力、合力矩求解块体线加速度与角加速度，再对时间积分求得块体速度与位移。重复上述计算过程，直至系统达到稳定状态或者发生失效。

1.2 离散元水力计算方法

离散元水力计算中，裂隙网络是流体运动的通道(块体不透水，但可变形)，流体在裂隙网络中的运动按平板层流模型，单位宽度的流量采用立方定理，即

考虑到裂隙水力开度增大时将导致雷诺数变大而超过层流的临界值，使水流变为紊流9- 10。同时，节理的水力开度不能降低到零，即使在很高的应力条件下节理中仍然会有少量的残余流体通过。Witherspoo[11]建议采用如下形式修改立方定律，即

式中，um为节理的法向变形；F为修正系数，比较式(9)与式(10)，有

Detournay提出节理的水力开度与节理的变形关系如下

uh=fum=uh0+fΔum

(12)

基于上式能更普遍采用立方定理来解释试验结果。由此可得到

未知参数uh0和f可以由试验结果按线性回归计算得出。式(10)和式(13)的有效性可由试验数据证实。Alvarez分析了已有的节理渗流的试验数据，也确认了修改立方定律的有效性。参数f反映了节理粗糙度对紊流的影响。对光滑平直的节理，f接近1.0；而对于具有一定高度起伏的不匹配节理，f小于1.0。

表1 优势裂隙特征

离散元中由线性的弹簧代表节理法向及切向刚度，节理的抗剪强度采用带剪胀角的摩尔-库仑本构模型。一般计算中假定f=1.0，而节理的初始水力开度及残余水力开度为模型参数，节理水力开度与有效应力关系可采用双线性或非线性关系。裂隙水力开度等于裂隙初始水力开度与裂隙面法向位移之和，裂隙的水力开度随块体的运动与变形发生变化。裂隙水力开度在法向荷载作用下，将趋于一残余值。裂隙交汇处，流体的运动服从连续方程。

2 数值模型建立与参数选择

2.1 模型建立

根据某工程地质构造(见图1)和优势裂隙发育情况(见表1)，选取高压隧洞的典型剖面建立DFN模型(见图2)。模型计算范围为：x向160 m、y向120 m。

图2 典型剖面DFN模型

2.2 模型计算

模型四周为位移约束边界；模型上下游水头边界按随高程线性变化设置，其中高压隧洞所在高程取325 m；模型底部为不透水边界，上部为自由边界；高压引水道钢筋混凝土衬砌段为定水头边界，水头根据不同的工况设定，钢衬段为不透水边界。考虑高压隧洞混凝土衬砌段固结灌浆情况，选取4种工况进行高压隧洞围岩裂隙渗透规律的计算分析，见表2。计算中所需的力学参数根据地质报告和相关规范及工程经验选取。岩体与节理裂隙力学参数分别见表3、4。

表2 计算工况

表3 岩体力学参数

表4 节理力学参数

3 优势渗透路径的分析

裂隙岩体优势渗透路径的形成因素是多方面的，一般而言可分为2类，一类称之为原生优势渗径，这类渗径是由于原生因素造成岩体的各向异性，如层理、裂隙等，致使介质导水能力不同，造成水流在介质中不均匀穿越；另一类称之为次生优势渗径，这类渗径是岩体在水-力作用下内部裂隙发生变形或形成新的扩张裂隙，使岩体内部水流发生了新的集中穿越。

根据数值模拟结果，高压隧洞围岩体裂隙渗流优势路径分布见图3。高压隧洞围岩体中，NW-NWW和SN向的节理裂隙渗透性较强，容易成为水流渗透的优势路径。其中，3号引支管左上侧f733附近为较明显的裂隙渗流优势路径，洞室周围裂隙在高水头下渗透性也较明显。工况①优势渗透路径的流量分布见图4。最大流量达到9.305×10-5m3/s，即5.6 L/min左右。

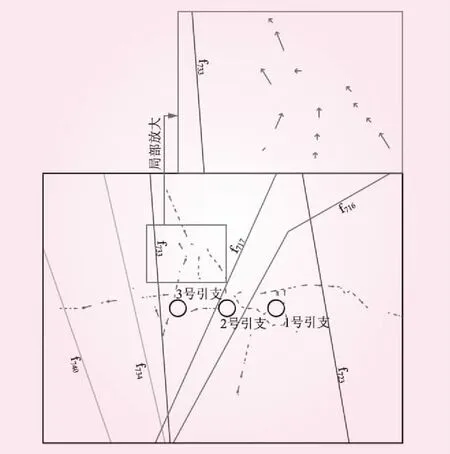
图3 优势渗透路径分布

图4 优势渗透通道的流量分布(单位：m3/s)

4 高压隧洞裂隙岩体渗控效应分析

高压隧洞在充水条件下，4种工况下裂隙水压力等值线分布数值分析结果见图5。从图5可知，裂隙水压力等值线从高压隧洞边缘向外凸呈依次降低趋势，隧洞周边断层附近区域表现出强渗透性。4种工况下沿断层f733的裂隙网络渗透性较强(方框范围)，水力梯度降低到1左右，与优势渗透路径相吻合。此外，1、2号引支管下部100 m左右也出现高水头与高水力梯度区域。

图5 裂隙水压力等值线(单位：m)

隧洞设置深度为4、6 m和8 m的高压固结灌浆后，高压隧洞外边缘水压力呈明显的下降趋势，表明固结灌浆圈起到了一定的防渗降压作用。但在高压隧洞进行8 m固结灌浆处理后，岔管分岔处的水力梯度依然达到35以上，表明高压隧洞设置固结灌浆起到了一定的防渗效果，但对降低水力梯度的效果有限。在岔管分岔处，可对围岩做进一步的固结灌浆或进行帷幕灌浆处理。

5 结 语

本文采用离散单元法，选取高压隧洞典型剖面建立数值模型，对高压隧洞裂隙岩体的优势渗透路径和渗控效应进行分析。结果表明，采用离散元数值分析法可以较为逼真地模拟高压隧洞裂隙岩体的渗透规律，真实反应裂隙岩体的优势渗透路径。高压隧围岩的优势渗流路径主要分布在断层和裂隙上。固结灌浆对防渗起到一定的效果，可有效地降低围岩的孔隙水压力及其水力梯度。但仅在固结灌浆的处理下，钢衬段裂隙水压力依然很大。本文分析方法可为工程进一步的渗控措施优化设计提供参考。