基于GPU的高效稀疏矩阵存储格式研究

程 , ,

(上海工程技术大学 电子电气工程学院,上海 201620)

0 概述

求解大规模稀疏线性系统是数值计算中的一个重要问题,广泛应用于力学、大气建模、地球物理、生物学、电路仿真以及计算科学与工程的其他领域。就大规模数值模拟而言,求解大规模稀疏线性系统Ax=f占据了大量的计算时间和资源,即需要计算稀疏矩阵A与向量x的乘积,这一类计算问题统称为稀疏矩阵与向量乘(Sparse Matrix-Vector Multiplication,SpMV)。电磁问题复杂程度的提高使得计算规模愈加扩大,如何加快大规模稀疏线性方程组的求解速度显得愈加重要,目前,解决该问题的重要方法之一就是运用高性能计算技术。

目前,常用的求解稀疏线性系统的方法有直接法与迭代法。直接法是通过对方程组的系数矩阵进行变换,将原方程组转化为形如三角矩阵等形式,继而使用回代或追赶的方法得到方程组的解。迭代法是从解的某个近似值出发,构造一个无穷序列去逼近精确解的过程。在实践中,迭代法受迭代矩阵的影响,其所适用于解的线性方程组类型不尽相同。当稀疏矩阵为病态矩阵时,舍入误差大大降低了收敛速度,因此,需用各种预处理技术加以改进以达到良好的计算效果。本文结合直接法的可靠性和迭代法的易并行性,采用不完全LU分解预条件共轭梯度(Incomplete LU factorization preconditioned Conjugate Gradient,ILUCG)法进行研究。

文献[1]提出IC/ILU预条件CG/BiCGSTAB算法,并采用CUBLAS[2]、CUSPARSE[3]库对其进行实现。文献[4]提出基于GPU的稀疏线性系统的预条件共轭梯度法,并采用对角预处理法实现算法。文献[5]在文献[1]和文献[4]方法的基础上,提出基于GPU加速的ICCG法。文献[6]研究基于GPU的矩阵乘法优化,提出一种基于HYB(Hybrid)格式的新存储格式。文献[7]研究了基于HYB格式稀疏矩阵与向量乘在CPU+GPU[8]异构系统中的实现与优化。

本文在文献[6-7]研究的基础上,提出一种稀疏矩阵的混合存储格式HEC(Hybrid ELL and CSR),并在CUDA[9]平台上实现基于HEC格式的ILUCG方法,以测试其加速效果。

1 存储格式

SpMV的求解是科学计算中的一个经典问题,为提升其运算性能,对稀疏矩阵存储格式的优化显得非常重要。文献[10]在CUDA平台上实现了利用不同的压缩存储格式的SpMV运算,并对性能进行了比较分析。文献[11]提出一种新的压缩矩阵存储格式CDIA(Compress format DIA gonal),并成功地在CUDA平台上对该方法进行实现。文献[12]针对CSR存储格式提出在GPU上的实现方法和优化策略。目前,这些对单一存储格式优化的研究取得了较大的进展,NVIDIA公司的CUSPARSE线性代数库也对这些单一的存储格式提供了强有力的支持。

然而,由于稀疏矩阵中非零元素分布的不规则性,导致采用单一的压缩存储格式进行运算时,取得的效果并不理想,因此多种对矩阵压缩存储格式进行优化的方法被相继提出:一种是对行进行合并分块来缓解行与行间非零元素差异过大的情况,如BCSR[13]格式、BELLPACK[14-15]格式等,此外,文献[16]研究了基于GPU的SpMV运算的优化,对分段行合并及按行分块存储策略进行了深刻剖析;另一种是采取混合格式进行存储,以适应不同矩阵不规则的稀疏特征。如针对准对角矩阵采用的DIA和CSR混合的HDC(Hybrid Dia and CSR)[17]存储格式以及混合ELL(ELLPACK)和COO(Coordinate)格式的HYB[18]存储格式等。

目前,HYB存储格式应用尤为广泛,现有的HYB Kernel函数大都是在GPU上运行ELL部分,在CPU上运行COO部分,进行异构计算,考虑到CSR格式存储的数据量较COO格式更少,且GPU具有天然的并行性,因此,本文提出一种矩阵的混合存储格式HEC,即将矩阵存储为ELL格式和CSR格式,并在GPU上运行该存储格式的Kernel函数,以获得一定的加速效果。

1.1 ELL存储格式

如图1所示,ELL格式用2个二维数组Values[ ]和Col[ ]来存储一个n×k的矩阵(k为包含非零元素最多行的非零元数目,这里为n为4,k为2),将一个稀疏矩阵采用类稠密的方式存储,更适合于并行计算。ELL格式对非零元较为集中于部分行的稀疏矩阵具有良好的存储效果,二维数组Values大小为n×k,它存储原稀疏矩阵中每行非零元的值,若该矩阵的所有行中最大非零元数为s,每行的非零元总数为c,则每行(s-c)的部分由0来填充;二维数组Col大小也为n×k,它用来存储相应非零元素在原系数矩阵中的列索引,它的相应位置也可以用0来填充。

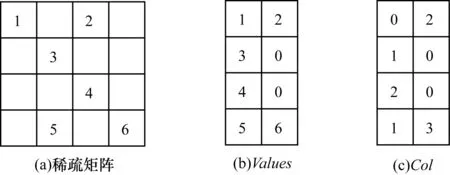
图1 ELL存储格式

ELL格式的优点是只用2个数组就可以存储一个稀疏矩阵,在一定程度上节省了存储空间,降低了访存开销,且其SpMV算法在加速器内易于并行实现。然而,ELL格式不适用于行之间非零元素相差较大的稀疏矩阵,若有一行每一个元素都是非零元,则ELL数组Values[ ]的列数和原稀疏矩阵的列数相等,就完全起不到压缩的效果。

1.2 CSR存储格式

如图2所示,CSR格式采用3个数组Values[ ]、Rowptr[ ]、Colind[ ]来存储一个稀疏矩阵,若矩阵的大小为n×n,且其总非零元数为m,则数组Values[ ]与Colind[ ]的长度为m,数组Values[ ]保存原稀疏矩阵中的所有非零元的值,数组Colind[ ]存储了各非零元在原稀疏矩阵中的列索引,数组Rowptr[ ]的长度为n+1,它存储了每一行元素在压缩存储格式中的起始位置。在图2中,数组Rowptr[ ]中的元素是每一行起始位置的指针,Rowptr[0]表示第0行,即从数组Values[ ]的0号位置1开始,Rowptr[1]表示第1行,即从数组Values[ ]的2号位置3开始,以此类推。

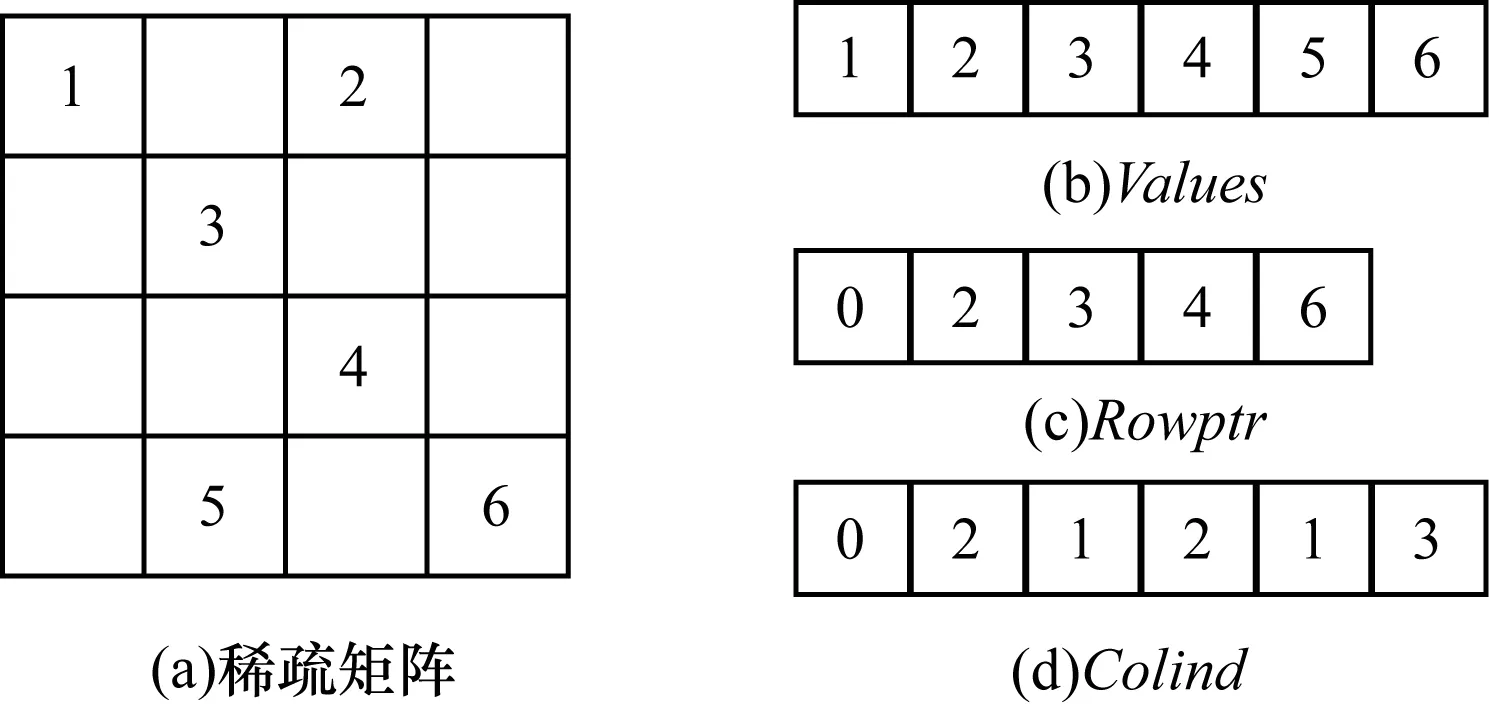
图2 CSR存储格式

需要注意的是,若原稀疏矩阵有一行元素全为0(以第1行元素全为0举例,该矩阵的行编号分别为0、1、2、3行),则Rowptr[1]与Rowptr[2]的值都是2,表示该存储格式中没有保存第1行的元素。CSR存储格式可有效地表示任何形式的稀疏矩阵,因此,其在目前大规模稀疏线性系统的科学计算中应用尤为广泛。

1.3 COO存储格式

如图3所示,COO格式采用3个数组Values[ ]、Row[ ]、Colind[ ]来存储一个稀疏矩阵,它与CSR格式的区别在于数组Row[ ]存储了原稀疏矩阵中所有非零元的行索引。

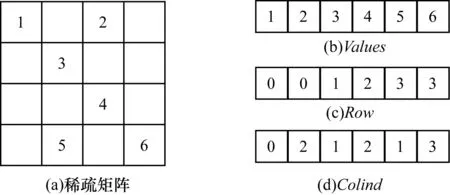
图3 COO存储格式

1.4 HYB存储格式

如图4所示,HYB存储格式由ELL与COO存储格式混合而成,用2个二维数组Values和Col来存储一个n×k的矩阵(k为包含非零元素最多行的非零元数目),二维数组Values大小为n×k,它存储稀疏矩阵中每行非零元的值;二维数组Col大小也为n×k,它存储稀疏矩阵中非零元的列索引。

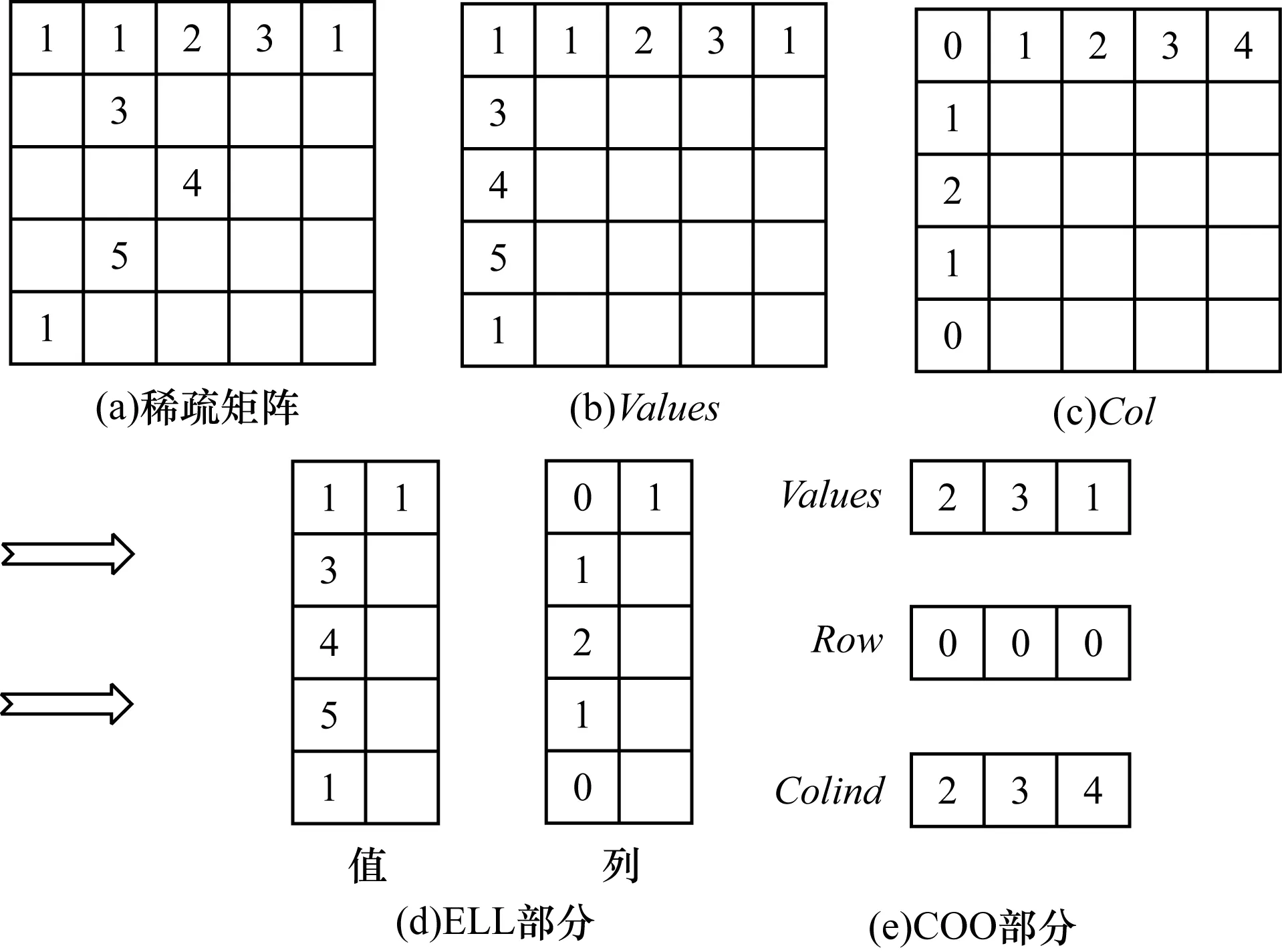
图4 HYB存储格式

HYB格式依据阈值K将矩阵划分为ELL格式与COO格式存储,即将数组Values第K(阈值)列左边的部分(包括K列)存储为ELL格式,右边的部分存储为COO格式。对于此,产生了一个重要的问题是阈值K的划分,即如何划分可以获取最优的性能,这里采取界限法,划分规则如下:

先求得ELL格式存储的矩阵,在这之中,若第K列的元素加到划分的ELL部分后,若ELL部分的总非零元数超过其总元素的二分之一,那么第K列将会被划到ELL部分。

阈值K划分算法描述如下:

求出第1列的非零元数

for j=2:1:sf

//j为矩阵Values的列,sf为矩阵Values的总列数

求出前j列的总非零元数s

求出前j列的元素的总数量c

IF s>(c/2),则 K=j;ELSE break

求出阈值K

例如,在图4中,在将稀疏矩阵的第1列划分为ELL格式后(共有4列,编号为1、2、3、4),若将第2列划分为ELL格式,则ELL部分元素的总数量为10,总非零元数为6>5,因此,第2列应该划分为ELL格式;若将第3列划也为ELL部分,则总元素为15,总非零元数为7<7.5。因此,第3列不应该被划分为ELL部分,即此时的阈值K应取2。

1.5 HEC存储格式

如图5所示,HEC格式由ELL与CSR存储格式混合而成,根据阈值K将矩阵划分为ELL格式与CSR格式两部分存储,阈值K的划分规则与HYB格式相同,即K仍取2。ELL部分的内容仍与HYB格式相应的部分相同,遍历剩余部分所有非零元的所在行,将其划分到CSR部分,由于剩余部分的3个数2、3、1位于同一行,因此CSR部分的数组Rowptr只需存储2个数0、3,即为起始位置索引0和划分到CSR部分元素的个数3。

图5 HEC存储格式

若存储为HYB格式,则COO部分的数组Row需存储 3个数0、0、0,即为原稀疏矩阵中相应部分各非零元的行索引。在本例中,稀疏矩阵的行列数及非零元数较少,相较于HYB格式只少存储了1个数,但在大规模稀疏线性系统的求解中,随着稀疏矩阵行列数及非零元数的增多,HEC存储格式的效率将会显著提升。

HEC格式保留了ELL格式适合于并行算法的优势,并且它可克服ELL格式只适合于矩阵各行间非零元数相差不大情况的缺点,从而减少填充元素的数量,因而其具有良好的性能。

此外,HEC存储格式比CSR格式多存储了2组数据Val_ELL和Col_ELL(分别为以ELL格式存储的值和列),会对读取带来一定的开销,但在真实应用中,SpMV操作会在下一个迭代求解器中对矩阵A反复进行。在每一次迭代求解时,向量x和向量y(y=Ax)会发生改变,但矩阵A不变,因此,生成HEC存储格式的工作可摊销在多次的迭代求解中。

2 不完全LU分解的预条件共轭梯度法

2.1 预条件共轭梯度法

本文采取的预条件共轭梯度法是通过采取一系列的预处理技术减少共轭梯度法中的迭代次数,从而加速其收敛的一种方法。

共轭梯度法[19]是迭代法的一种,迭代法采用逐次逼近并用迭代公式得到一系列近似解,从而逐渐地逼近于真实解,最终可得满足一定误差条件的近似解。共轭梯度法是依赖于向量正交性的,对舍入误差的影响十分敏感,其收敛速度和系数矩阵的条件数紧密相关。理论上,它用小于n(矩阵的大小为n×n)的迭代次数即可得到求解结果。但当稀疏矩阵呈现病态时,在舍入误差的影响下,迭代次数大于n,收敛速度较慢,会出现数值解与理论解严重偏离的现象。

文献[20]对共轭梯度法进行分块处理,最终得到解决最小二乘问题的算法。

2.2 不完全LU分解

不完全LU分解是一种相当高效的预处理技术。LU分解是矩阵分解的一种,可将一个矩阵分解为一个下三角矩阵和上三角矩阵的乘积,或为上、下三角矩阵和一个置换矩阵的乘积。对式(1),若n阶稀疏矩阵A对称且正定,则如式(2)所示,可确定一个正定矩阵M,在求解向量x时可比式(1)获得更好的性能,矩阵M称为预处理矩阵,构造预处理矩阵的方法[21]有多种,如对角预处理构造法、多项式预处理构造法和不完全LU分解预处理法,本文正是采用了不完全LU分解预处理法。

在式(1)中,对n阶稀疏矩阵A进行分裂式近似分解,可得式(3),其中,L为下三角矩阵,P为剩余矩阵。式(2)为预处理后的方程组,矩阵M与矩阵A具有相似的稀疏性,因此,为提高算法的求解速率,用矩阵M代替矩阵A进行迭代运算。若将矩阵M进行LU分解,可得式(4),其中,LM为下三角矩阵,UM为上三角矩阵。

Ax=f

(1)

M-1Ax=M-1f

(2)

A=LLT+P=M+P

(3)

A≈M=LMUM

(4)

2.3 ILUCG算法

基于LU分解的ILUCG算法描述如下:

设定初值x0

r=f-Ax0,p=r,rw=r

for i=0,1,2,3,…,maxit

ρi=rwT×r

if ρi==0.0 then?

method failed

end if

求解 M×ph=p,得到ph

计算q,q=A×ph

s=r-α×q

x=x+α×ph

if ‖s‖2≤tol then

method converged

endif

求解 M×sh=s,得到sh

计算 t=A×sh

求得 x=x+ω×sh

求得 r=s-ω×t

end for

3 算法实现

3.1 基于CUSPARSE和CUBLAS库的ILUCG法

利用CUDA中的CUSPARSE和CUBLAS库可以对ILUCG算法进行实现,在运算过程中,GPU负责迭代前和每次迭代过程中的矩阵与向量,向量与向量间的并行计算,CPU负责迭代循环和收敛条件的控制以及标量相除等操作。算法描述如下:

初始化CUSPARSE和CUBLAS库

对矩阵A进行不完全LU分解,得到一个下三角矩阵L和上三角矩阵U,分别读取矩阵A、L、U的值、行索引和列,分别为(Data,Row_ptr,Col_index)、(data_L,row_ptrL,col_indexL)、(data_U,row_ptrU,col_indexU)

创建descr_L、descr_U、descr_A、info_L、info_U并初始化

用cudaMalloc函数给各变量分配内存

用cudaMemcpy进行数据传输

用cusparseDcsrsv_analysis函数生成info_L、info_U

用cusparseDcsrmv函数计算r=A×x0

用cusparseDcsr2hyb函数将矩阵A以HYB格式保存在hybA中

用cusparseDhybmv函数计算r=A×x0//以HYB格式计算

用cublasDscal函数计算r=-r

用cublasDaxpy函数计算r=b+r=-A×x0+b

用cublasDcopy函数赋值p=r,rw=r

用cublasDnrm2计算nrmr0=(r12+r22+…+rN2)0.5

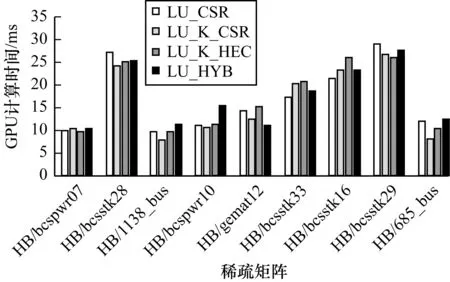
for(i=0;i

rhop=rho,进行rho值的更新,使得rhop[i]=rho[i-1]

用cublasDdot函数计算內积(r,rw)

if (i>0) then

β=(rho/rhop)×(α/ω)

用cublasDaxpy、cublasDscal函数计算p=r+β×(p-ω×q)

end if

用cusparseDcsrsv_solve函数计算ph,ph=M-1×p

A.用cusparseDcsrmv函数计算q=A×ph

B.用cusparseDhybmv函数计算q=A×ph

用cublasDdot函数计算內积(r,q),即temp=rT×q

计算a=rho/temp

用cublasDaxpy函数计算s=r-a×q,x=x+a×ph

用cublasDnrm2计算nrmr=(r12+r22+...+rN2)0.5

若(nrmr/nrmr0)

用cusparseDcsrsv_solve函数计算sh,sh=M-1×s

用cusparseDcsrmv函数计算t=A×sh

用cusparseDhybmv函数计算t=A×sh

用cublasDaxpy函数计算x,x=x+w×sh,r=s-w×t

用cublasDnrm2计算nrmr=(r12+r22+...+rN2)0.5

If (nrmr/nrmr0)

//tol为自设允许的误差范围,这里取10-6

end for

3.2 基于CUDA的SpMV算法

3.2.1 基于CSR存储格式的SpMV算法

在不完全Cholesky分解预条件共轭梯度算法中SpMV运算的操作可由自作的GPU Kernel函数完成,使用cudaStream_t(CUDA流)以提高程序的执行效率。若将矩阵A以CSR格式存储,则有Kernel函数如下:

__global__void SpMV_CSR(double *data ,int *col_index,int *row_ptr,double *x,double *y)

{

int elem;

int row =blockIdx.x*blockDim.x + threadIdx.x;

if(row< N) //N为矩阵A的行数

{

float dot=0;

int row_start=row_ptr[row];

int row_end=row_ptr[row+1];

for(elem=row_start;elem

{

dot+=data[elem]* x[col_index[elem]];

}

y[row]=dot;

}

}

3.2.2 基于HEC存储格式的SpMV算法

若将稀疏矩阵A以HEC格式存储,可调用SpMV_ELL和SpMV_CSR 函数分别计算划分到ELL和CSR部分的值并保存在数组y[row]和y2[row]中,最终,将y[row]与y2[row]的相应值相加,可得一次SpMV运算的结果。

基于HEC存储格式的SpMV算法如下:

__global__voidSpMV_ELL(double *data ,int *col_index,double *x,double *y)//GPU ELL Kernel函数

{

int i;

int row =blockIdx.x*blockDim.x + threadIdx.x;

if(row< P)//P为所划分出的ELL格式的总行数

{

float dot=0;

for(i=0;i

{

dot+=data[row+i*P]* x[col_index[row+i*P]];

}

y[row]=dot;

}

}

__global__ voidSpMV_CSR(double *data2 ,int *col_index2,int *row_ptr,double *x,double *y2) //GPU CSR Kernel函数

{

int elem;

int row2 =blockIdx.x*blockDim.x + threadIdx.x;

if(row2< P)

{

float dot=0;

int row_start=row_ptr[row2];

int row_end=row_ptr[row2+1];

for(elem=row_start;elem

{

dot+=data2[elem]* x[col_index2[elem]];

}

y2[row2]=dot;

}

}

4 实验与结果分析

本文实验的计算平台,其CPU为Intel Core(TM) i5-6500 @3.20 GHz;GPU为NVIDIA GeForce GTX1050;运行内存(RAM)的大小为8 GB;系统为Windows7 64位;实验环境为Visual Studio 2012,CUDA8.0。测试所用稀疏矩阵全部来自UF Sparse Matrix Collection[22],即佛罗里达大学的稀疏矩阵集,如表1所示。

表1 测试所用稀疏矩阵

4.1 总时间对比

分别运用调用CUSPARSE库函数cusparse Dcsrmv()、cusparseDhybmv()和调用GPU Kernel SpMV_CSR、SpMV_HEC的方式进行SpMV运算,并调用计时函数clock_t()记录下基于LU分解的ILUCG法的总运算时间,运行50次,取平均值。其中:

1)在调用cusparseDhybmv()函数进行SpMV运算前,需先调用cusparseDcsr2hyb()函数将CSR格式存储的稀疏矩阵信息转换为HYB格式进行存储并保存在hybA中。

2)总时间=CPU向GPU数据传输时间+GPU计算时间。

上述指标对比如图6所示。其中,LU_CSR、LU_HYB分别代表以CSR、HYB为稀疏矩阵的存储格式并调用CUSPARSE库函数进行运算的实现方式。LU_K_CSR、LU_K_HEC分别代表以CSR、HEC为存储格式并调用GPU Kernel进行运算的实现方式。

图6 4种实现方式的总时间对比

由图6可知,LU_K_HEC的实现方式对本次实验所测试的矩阵具有良好的性能,当稀疏矩阵为HB/bcsstk29 时,以该实现方式在4种方式中耗时最短,可获得最优的加速效果,为10.4%。一方面,这是由于矩阵HB/bcsstk29具有对角特征,行中的非零元素较为均衡,分布在对角线之外的元素稀少,分割出来的ELL矩阵进行数据(0)的填充较少,因而具有较好的加速效果;另一方面,相较于HYB的存储方式,该方式存储的非零元更少,更利于其发挥在内存读取与数据传输方面的优势;相较于CSR的存储方式,矩阵 HB/bcsstk29有较多的非零元,可抵消函数调用带来的损耗,更利于GPU的并行化处理,从而缩短GPU的计算时间。

4.2 GPU计算时间对比

图7展示了GPU计算时间的对比情况,GPU计算时间即运用GPU处理整个预条件共轭梯度法的运算时间,计时方法采用调用CUDA函数cudaEvent_t()进行计时。

图7 4种实现方式的GPU计算时间对比

从图7可以看出,对于多数矩阵,LU_K_CSR的实现方式耗时最短,这是由于这些矩阵的非零元数较少,以CSR格式进行存储相较于HEC格式进行存储,只需调用一个函数,减少了计算损耗。对于矩阵HB/bcsstk33,它比HB/bcsstk28有更多的非零元,花费的计算时间却相近,原因是该矩阵经LU分解后所得到的矩阵L和U有更少的非零元数,减少了GPU的计算时间。而对于矩阵HB/bcsstk29,LU_K_HEC的实现方式耗时最短,表明HEC存储格式对大型稀疏线性矩阵有良好的存储效率。

5 结束语

本文提出一种稀疏矩阵的存储格式HEC,并将其以ILUCG法中调用GPU Kernel的方式应用于大型稀疏线性系统的求解中,与利用CUSPARSE库函数cusparseDcsrmv()、cusparseDhybmv()的实现方式相比,最高可得到10.4%的加速效果。

在应用领域,矢量有限元法是求解电磁问题的重要方法之一,该方法将一个离散后的线性系统归结为方程Ax=b的求解,而电磁问题的复杂化使得系数矩阵A愈加不规则,因而可以考虑通过多次划分ELL格式进行存储,以用于更加不规则的线性方程组计算。同时,建立一个稀疏矩阵存储格式的优选模型,根据不同矩阵的特点选取最优的存储格式以提升计算效率,也将是下一步的研究方向。