蒙代尔-弗莱明模型可控性与仿真

王祥兵

（贵州工程应用技术学院 经济与管理学院，贵州 毕节 551700）

蒙代尔-弗莱明模型是讨论经济开放条件下财政政策和货币政策对宏观经济影响的标准工具，是Fleming[1]和Mundell[2]在封闭经济系统IS-LM模型中，引入了资本流动和国际贸易等开放经济因素提出的。蒙代尔-弗莱明模型将IS-LM模型所分析的由产品市场、货币市场组成的内部均衡拓展至由国际市场、产品市场和货币市场组成的开放经济系统的一般均衡分析，并为分析开放经济系统的一般均衡提供简洁的理论框架工具。现实开放经济系统中各种经济变量总是随时间变化不断地进行调整，如利率、汇率、价格、税率、总需求、总供给、政府支出、净出口、投资和消费等变量随时间而发生变化。各种经济变量调整和变动都会对开放经济系统的动态演化产生深刻影响，导致开放经济系统呈现出不断地波动、非均衡状态和经济失衡。为了熨平经济波动与失衡对经济发展的负面影响，政府必须依据宏观经济发展态势来设计相应的财政政策和货币政策，以期有效调整与控制经济系统演化状态，这就为本文研究提供了切入点。

控制理论和方法主要用于解决工程领域问题[3]，近年来，用控制理论和方法研究经济与管理问题也逐渐增多，取得了丰富的成果。Hochschulassistent等[4]对连续的宏观经济动态系统可控性进行研究，研究表明，许多动力系统可以在任意给定的时间路径通过脉冲控制实现引导目标。Phillip等[5]对基于闭环最优控制的变结构控制方法进行研究，研究表明，如果系统参数存在错误，则传统的闭环优化控制解决方案就会变得不稳定，而变结构控制方法却存在稳定解。雷勇[6]弱化了非均衡微观市场干扰条件，对非均衡蛛网模型的市场价格调节与控制策略进行研究。熊焰等[7]构建修正的乘数-加速数模型，对模型的稳定性、能控性和能观性进行分析，并利用我国统计数据对该经济系统进行仿真分析。焦红兵等[8]研究了一类以CES生产函数为反馈的定常经济模型的稳定性，并证明非定常经济模型的解析解是全局渐进稳定的。孙剑飞等[9]认为，采用比较静态分析的总需求-总供给模型，没有有效考虑动态经济因素对经济系统的影响。把动态经济因素引入总需求-总供给模型，建立了总需求-总供给模型的无模型控制，进而得到总需求-总供给模型的无模型控制律。龚德恩[10]利用动态经济理论构建动态IS-LM模型系统，对封闭经济系统中的财政政策和货币政策的优化与设计问题进行了分析。甄子洋等[11]利用信息融合最优估计方法针对未来干扰无预见和期望输出的线性系统最优跟踪问题进行研究，得到该问题的近似最优融合控制律，并以一类宏观经济系统为例进行仿真研究。Anisimov等[12]对人力资源变量波动条件下基于混合约束的一部门经济增长模型的最优控制问题进行分析和仿真研究。

综合上述分析，现有成果主要是针对封闭经济系统进行研究，而实际经济系统必然受到外部（国际）经济的影响，是动态开放的系统。因此，必须对现有封闭经济模型进行拓展，将国际市场引入，以更符合经济发展实际。同时，现有研究中投资函数仅考虑消费增长作为拉动经济增长的基本因素，没有考虑消费与净出口增长同时作为拉动经济增长的情形。基于此，本文同时考虑消费与净出口增长作为拉动经济增长的因素，探讨由国际市场、商品市场以及货币市场构成的复杂开放经济系统可控制性问题。由于开放经济蒙代尔-弗莱明模型系统与封闭经济LS-LM模型系统相比，其控制变量、状态变量和干扰变量发生了变化，具有许多与封闭经济LSLM模型系统不同的特性，故开放经济蒙代尔-弗莱明模型系统的政策控制难度加大，其控制策略与政策设计也有很大差异。为此，本文首先构建动态蒙代尔-弗莱明模型，再对动态蒙代尔-弗莱明模型的能达性、能观性和能控性进行分析；然后对动态蒙代尔-弗莱明模型的纯增益反馈控制律进行求解，并对其解析解的政策意涵进行分析和仿真研究。

1 蒙代尔-弗莱明动态模型建立

通常蒙代尔-弗莱明模型是由供需均衡的国际市场、商品市场和货币市场组成的静态模型系统，但实际经济系统是动态演化的，即国际市场、商品市场和货币市场均为非均衡的。当国际市场出现非均衡时，实际汇率则会变动以调节国际需求；当商品市场出现非均衡时，总供给发生相应调整；当货币市场出现非均衡时，利率则会变动以调节货币供求。根据上述分析，可构造蒙代尔-弗莱明的动态模型：

（1）商品市场。总需求方程为

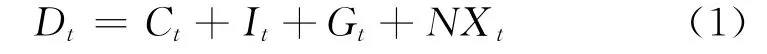
式中，Dt、NX t、Gt、Ct、It分别为t期的总需求、净出口需求、政府支出需求、消费需求和投资需求。

消费函数为

可支配收入方程为

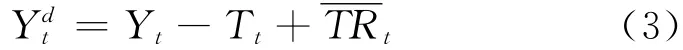
税收方程为

式中，τ为边际税率。

投资函数为

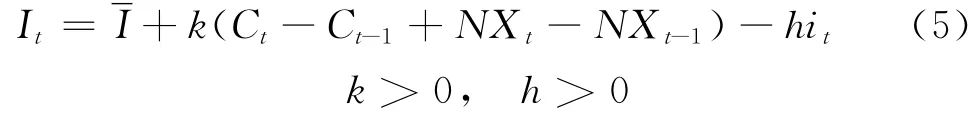
式中，k、it分别为投资加速数和t期的利率。

总供给方程为

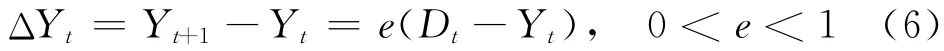
式（6）表明，当商品市场供给大于需求（D t＜Y t）时，库存增加，生产者会减少生产，故下期总供给减少；当商品市场供给小于需求（Dt＞Y t）时，生产者会增加生产，故下期总供给增加。

（2）货币市场。货币总需求函数为

式中，分别为自发性货币需求和t期的货币需求。

利率调节方程为

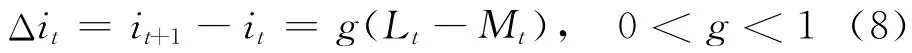
式（8）表明，当货币供给大于货币需求（L t＜M t）时，下期利率会下降；反之，当货币供给不足（L t＞M t）时，下期将利率会上升。

（3）国际市场。净出口函数为

式中：、γ、n均为外生参数；EP f/P=Et；分别为t期的实际汇率和自发性净出口水平。

实际汇率调节方程为

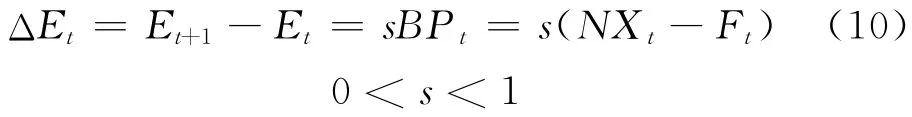
式中，Ft、BP t分别为净资本流出和t期国际收支差额。式（10）表明，当国际收支逆差（NX t＜Ft）时，下期实际汇率会下降；反之，当国际收支顺差（NX t＞Ft）时，下期实际汇率将会上升。

（4）蒙代尔-弗莱明模型的控制目标和变量。动态蒙代尔-弗莱明系统中，政府调控有3个目标：①希望总产出Y t按照预先给定增长率δ增长，即总产出Y t趋向计划总供给Y*=Y0（1+δ）t；②希望利率稳定在预先给定水平，即利率it趋向预先给定适当的利率i*；③实际汇率稳定在预先给定水平，即Et趋向预先给定适当的汇率水平E*，则

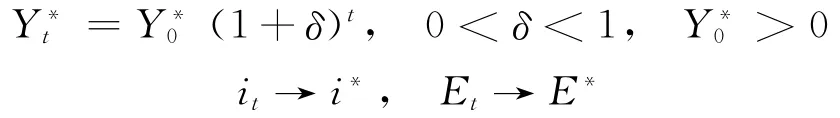
根据纯增益反馈控制律的设计要求和动态蒙代尔-弗莱明系统的控制目标控制，系统的输出变量y（t）可以用矢量形式表示，即

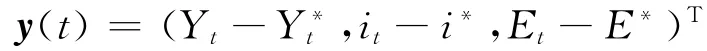
净资本流出Ft、货币发行量Mt、政府支出需求Gt分别为动态蒙代尔-弗莱明系统中的汇率政策、货币政策和财政政策的代表变量，也是系统的控制输入变量，其矢量形式u（t）=（Gt，M t，Ft）T。

系统的状态变量为t期的消费Ct、投资It、总产出Y t、利率it、实际汇率Et，其矢量形式x（t）=（Ct，It，Y t，it，Et）T。

系统的干扰输入变量为自发性的消费、投资、货币需求、转移支付以及计划总供给Y*、目标利率i*、目标汇率E*。其矢量形式为

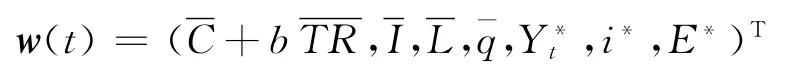
（5）蒙代尔-弗莱明模型的状态空间形式。将式（3）、（4）代入式（2），可得

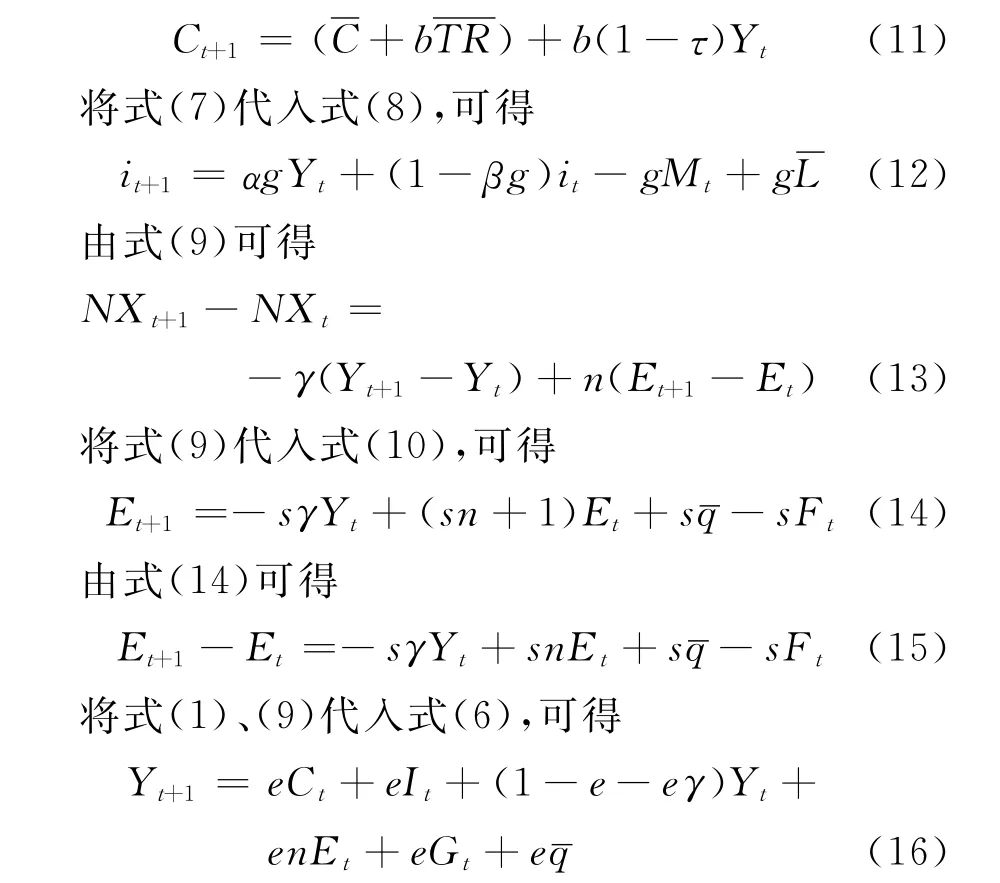
将式（15）、（16）代入式（13），可得

由式（11）、（18）、（16）以及式（12）、（14）构成MF模型的动态系统：

将式（19）转换为状态空间形式：

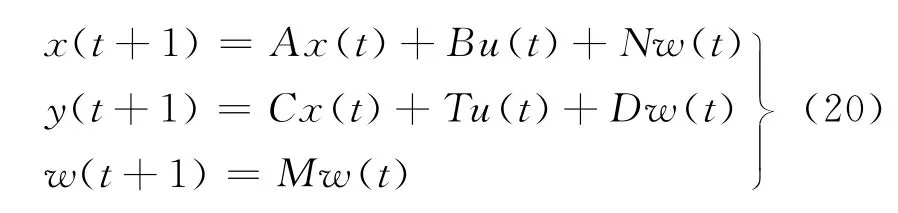
式（20）中有个方程分别为动态蒙代尔-弗莱明系统的装置方程、输出误差方程和外扰模型方程。

式（20）的系数矩阵分别为：

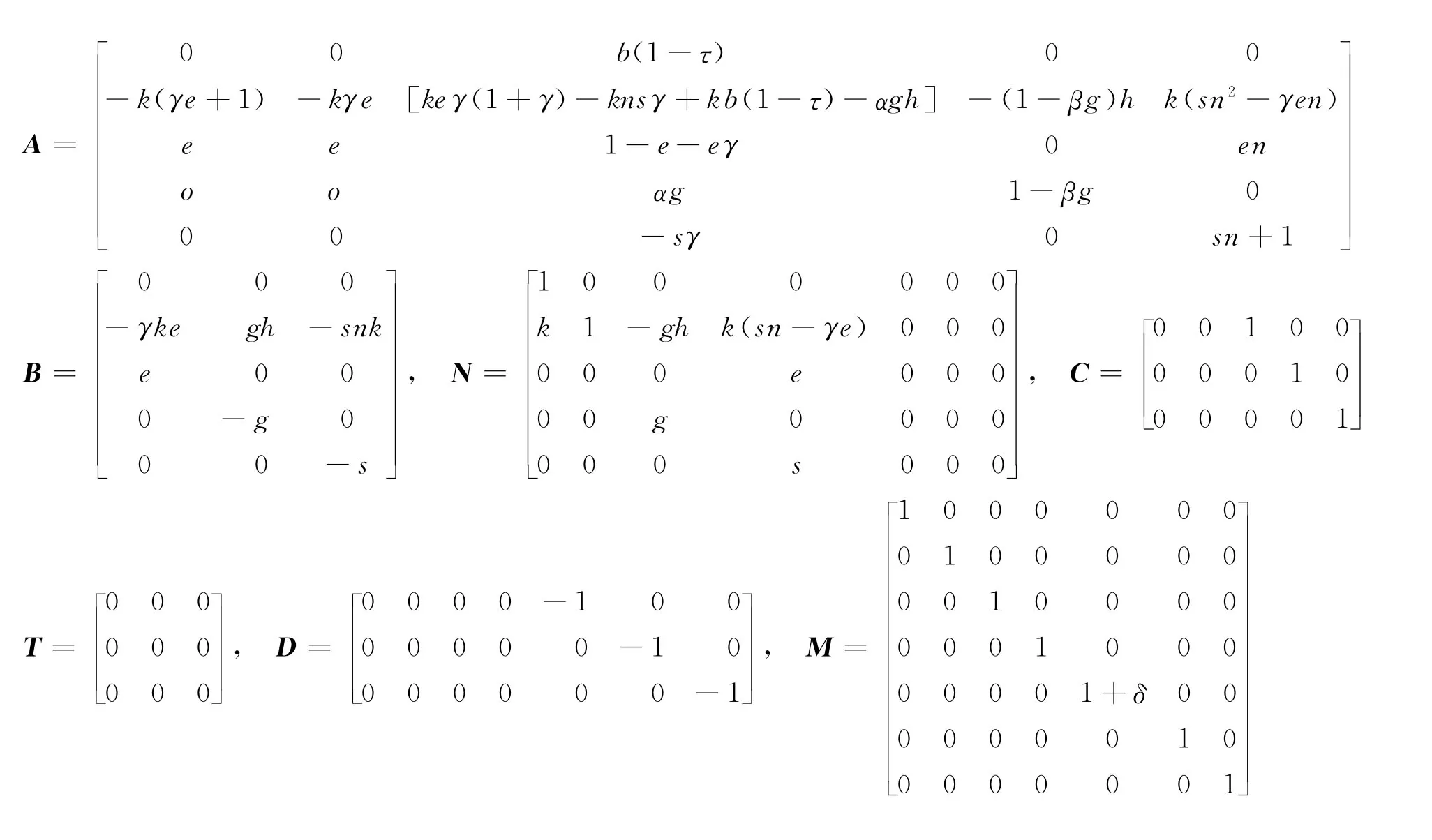
2 动态蒙代尔-弗莱明模型的系统分析

对于实际经济系统而言，决策者总希望通过系统的输入信号对系统运行状态进行完全控制，使系统具有预期的动态性能。因此，有必要对蒙代尔-弗莱明动态经济系统的能达性、能控性和能观性等系统结构特性进行分析。

2.1 系统能达性和能控性

定理1动态蒙代尔-弗莱明模型系统具有能达性与能控性。

证明

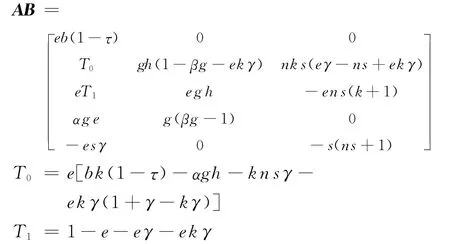
设矩阵A、B第1、3列向量以及矩阵B的列向量构成矩阵：

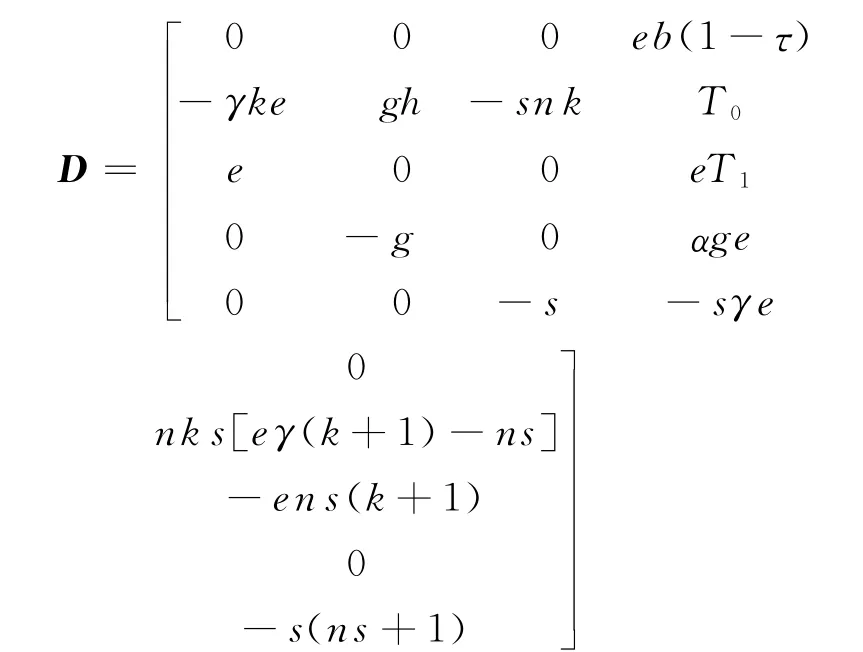
计算矩阵D的行列式，可得：

即动态蒙代尔-弗莱明模型系统的能控矩阵Q c的秩为5。因此，动态蒙代尔-弗莱明模型系统具有能达性和能控性。

2.2 系统能观性

定理2动态蒙代尔-弗莱明系统具有完全能观性。

证明设C=[c1c2c3]，其中，c i为矩阵C的行向量，由c1、c2、c3、c1A、c1、A2组成矩阵：

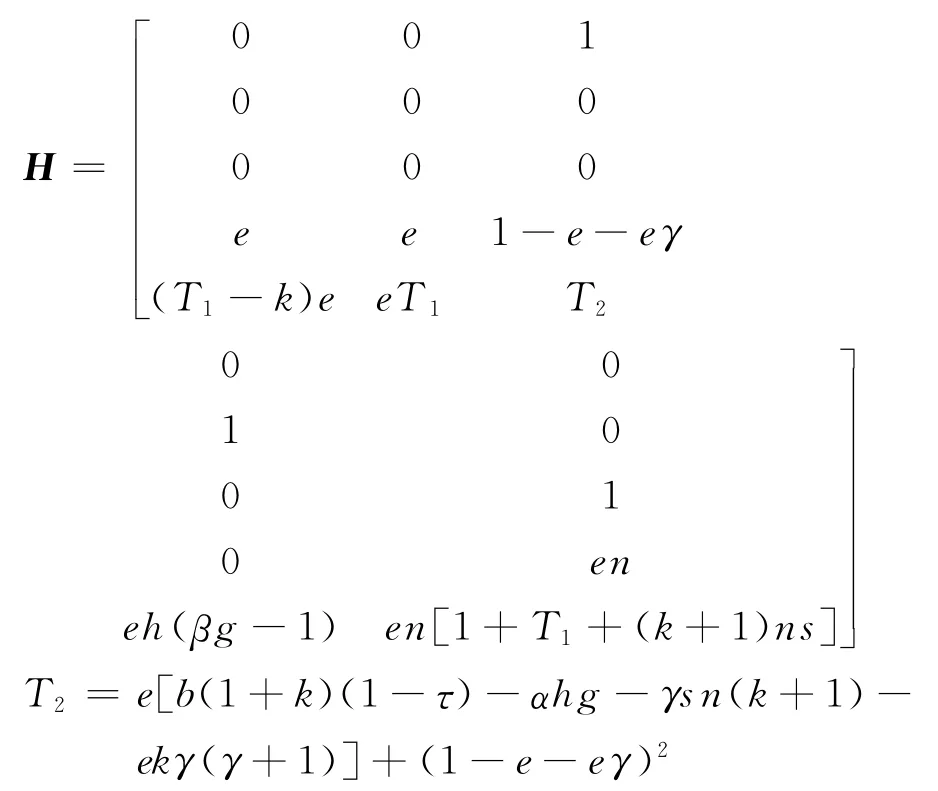
计算矩阵H的行列式可得：

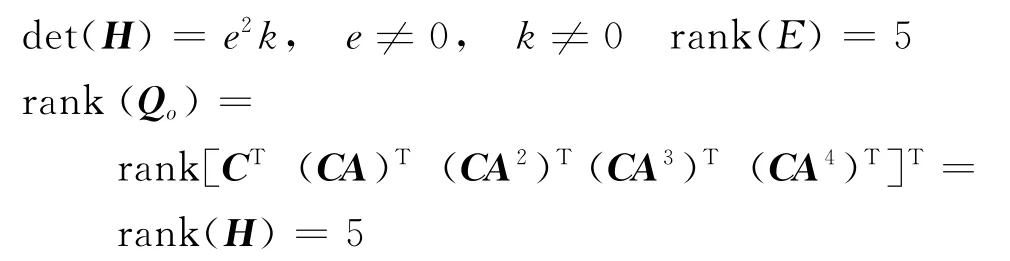
即动态蒙代尔-弗莱明系统能观矩阵Q o的秩为5。因此，动态蒙代尔-弗莱明系统具有完全能观性。

动态蒙代尔-弗莱明系统的状态x（t）具有能达性、能控性、完全能观性。根据现代控制理论，可以任意配置动态蒙代尔-弗莱明模型闭环系统的极点，使系统渐进稳定并具有良好的动态性能。

3 动态蒙代尔-弗莱明系统控制律的设计

动态蒙代尔-弗莱明系统的外部干扰输入为w（t），其纯增益反馈控制器为u（t），通过配置动态蒙代尔-弗莱明模型闭环系统的极点，使系统渐进稳定，同时达到输出调节，即动态蒙代尔-弗莱明系统的输出趋向于0，即

假设系统的状态反馈控制律

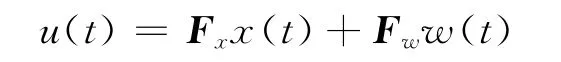
其中：F x为镇定矩阵；F w为伺服矩阵。根据动态蒙代尔-弗莱明系统的控制目标，动态蒙代尔-弗莱明模型闭环系统必须渐进稳定。因此，设计F x的原则是使A+BF x为渐进稳定矩阵，并且系统具有良好的动态响应过程，即矩阵A+BF x的特征值必须都在复平面的单位圆内；设计F w的原则是系统输出误差的静态值必须为0。根据系统静态误差的装置条件[10，13]，可知F w必须满足

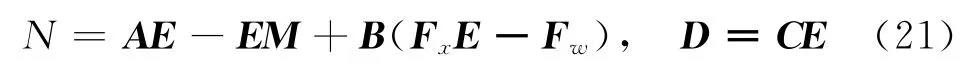
式中，E为5×7阶未知矩阵。

3.1 求解Fx

由于动态蒙代尔-弗莱明系统的状态x（t）具有能达性和完全能控性，可以任意配置动态蒙代尔-弗莱明模型的闭环系统极点，使其闭环系统渐进稳定。根据设计F x的原则，矩阵A+BF x的特征值必须都在复平面的单位圆内。假设任意给定的5个复平面的单位圆内极点｛λ1，λ2，λ3，λ4，λ5｝为矩阵A+BF x的特征值。

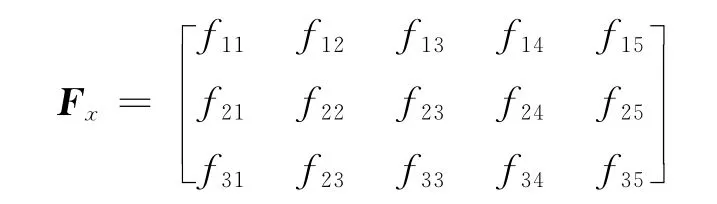
为使A+BF x渐进稳定矩阵并具有良好的动态响应过程，可取

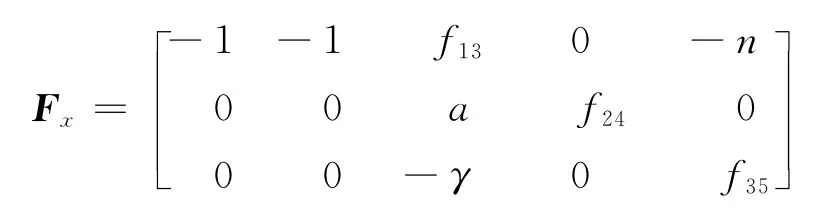
蒙代尔-弗莱明模型的闭环系统特征多项式为

化简可得

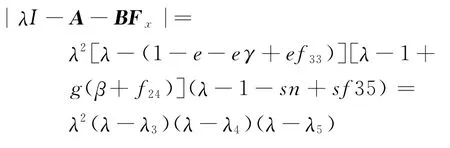
则

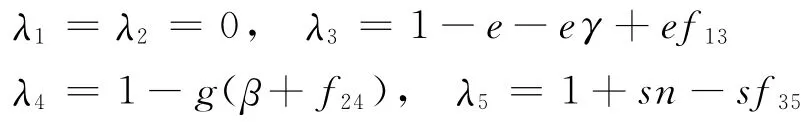
根据设计镇定矩阵F x的原则，f13、f24、f35取值分别使

3.2 求解Fw

设F x E-F w=Q，Q为3×7矩阵。由式（21）可得矩阵方程：

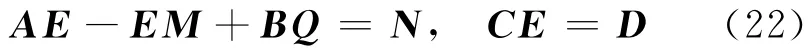
对矩阵C、E、D作分块：

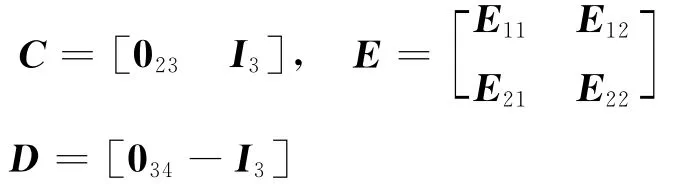
其中：E11、E12、E21、E22为2×4、2×3、3×4、3×3阶矩阵；I为单位矩阵，其脚码是其阶数，零矩阵脚码也是其阶数。将上述分块矩阵分别代入CE=D，可得

解式（23）可得：E21=034，E22=-I3。

对矩阵A、B、M、N、Q作分块：

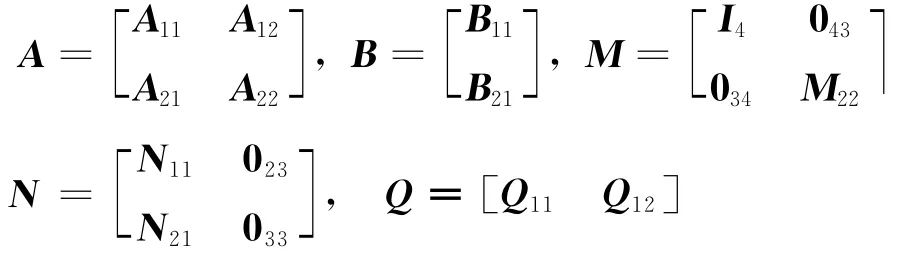
其 中，A11、A12、A21、A22、B11、B21、N11、N21、Q11、Q12、M22为2×2、2×3、3×2、3×3、2×3、3×3、2×4、3×4、3×4、3×3、3×3阶矩阵。将上述分块矩阵代入AE-EM+BQ=N，可得：

对式（26）第1式求解，可得

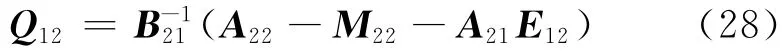
将式（28）代入式（26）第2式，可得

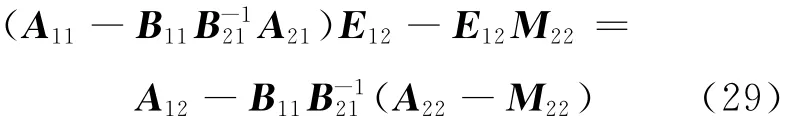
将矩阵A、B的分块矩阵代入式（29），化简得到Sylvester型方程：

其中，

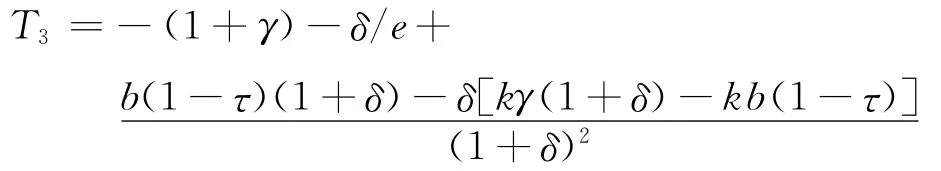
因此，可得：

其中：

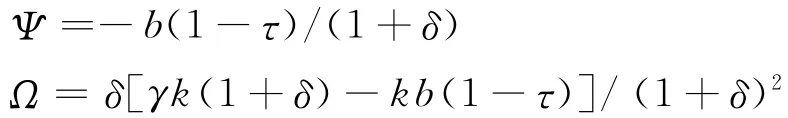
由F x E-F w=Q可知，F w=F x E-Q，将F x、E、Q代 入可得

其中，Π=1+γ+δ/e-f13。

将F x、F w代入u（t）=F x x（t）+F w w（t），可得控制律的解析解：

将式（31）回代到动态蒙代尔-弗莱明系统，可得：

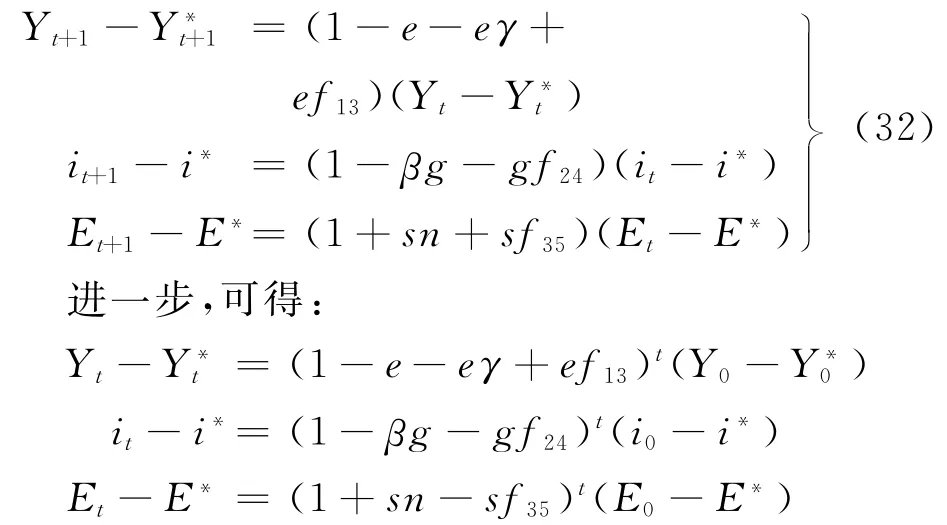
根据前面假设可知，f13、f24、f35取值分别使。因为

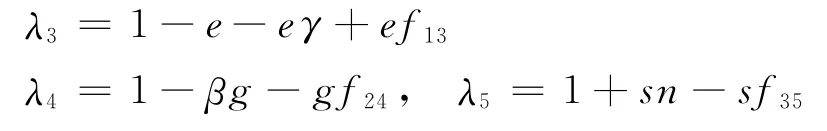
的模小于1，所以有：

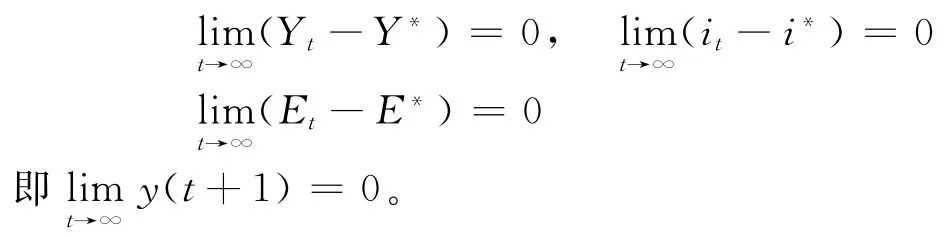
定理3动态蒙代尔-弗莱明系统可通过纯增益反馈控制器（式31），使其闭环系统渐进稳定，达到输出调节。

定理3表明，可以通过设计适当控制器，使动态蒙代尔-弗莱明系统渐进稳定，并使系统具有预期的动态性能，实现对动态蒙代尔-弗莱明系统的控制目标。

对式（31）作变换：

由假设可知：

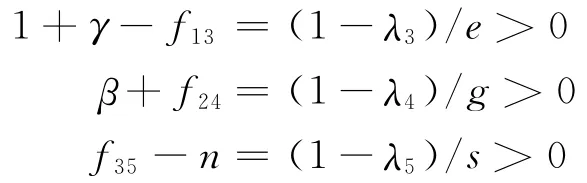
动态蒙代尔-弗莱明系统的反馈控制律u（t）的经济意涵为：式（33）表明，财政政策变量Gt的调节机制为：在即期总供给中扣除即期的净出口需求、投资及消费（Y t-Ct-It-NX t）的基础上，与即期总供给和计划总供给之差（Y t-Y*）反向变化，与计划总供给Y*同向变化。式（34）表明，货币政策变量M t的调节机制为：在即期货币需求的基础上，与即期利率和计划利率之差（it-i*）同向变化。式（35）表明，汇率政策变量Ft的调节机制为：在即期净出口需求的基础上，与即期汇率和计划汇率之差（Et-E*）同向变化。

4 仿真分析

为验证所设计的纯增益反馈控制律对动态蒙代尔-弗莱明系统控制的有效性，利用数字算例对动态蒙代尔-弗莱明系统演化过程控制进行仿真，仿真工具为MATLAB7.11。

4.1 仿真参数设置与数据说明

为充分体现和仿真式（31）所设计的控制律对动态蒙代尔-弗莱明系统控制的有效性，对式（19）共涉及22个参变量的设置做如下说明：①参变量所赋的值必须满足参数的经济意义和模型要求；②参变量所赋的值必须体现动态蒙代尔-弗莱明系统作为刻画开放经济系统框架工具的一般性，即参数除了满足条件①外任意选取也能实现对系统的有效控制；③参变量所赋的值应选取使得动态蒙代尔-弗莱明系统产生剧烈波动和失衡状态数值，才能更好地说明式（31）所设计的控制律对动态蒙代尔-弗莱明系统控制的有效性以及本文理论分析。因此，参数设置为：b=0.4，τ=0.18，k=3.7，α=0.2，β=50，h=60，e=0.056，s=0.005，g=0.002，γ=4.17，n=9.8，δ=0.05，λ3=0.6，λ4=0.7，λ5=。其中，的单位为102亿元。在上述设置下，系统的状态变量x（t）=（Ct，It，Y t，it，Et）T的初始值为（1，0.7，3，0.02，5）T，其中，消费Ct、投资It、总产出Y t的单位均为102亿元，汇率Et的单位为元。系统的干扰输入变量w（t）的初始值为（1.25，0.7，1，0.6，3，0.005，6）T。而政府调控目标为：①总产出Y t按照预先给定增长率δ增长，即Y t趋向计划总供给Y*=3（1+0.05）t；②利率稳定在预先给定水平，即利率it趋向给定利率i*=0.005；③实际汇率稳定在预先给定水平，即Et趋向给定汇率水平E*=6元。

4.2 仿真结果分析

在上述参数设置下，取100个时间单位，对蒙代尔-弗莱明系统进行仿真，仿真效果如图1所示。

图1 无控制条件下蒙代尔-弗莱明模型系统的演化图

为了熨平经济剧烈波动与失衡对经济发展的负面影响，政府需根据经济变量如消费Ct、投资It、总产出Y t、利率it和汇率E t等发展态势来设计相应的财政政策变量Gt、货币政策变量Mt和汇率政策变量F t，以期有效调整与控制经济系统演化状态。根据控制目标和经济变量变化情况，利用式（31）所设计的政策变量控制律对蒙代尔-弗莱明系统进行控制，加入控制后的仿真曲线如图2所示。

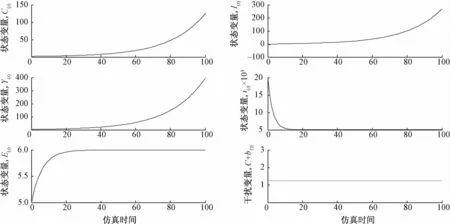
图2 加入控制后蒙代尔-弗莱明模型系统的演化图

Y*=3×（1+0.05）100=394.503 8×102亿元

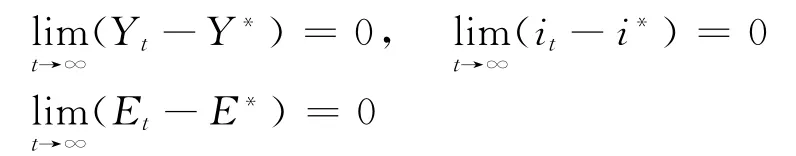
即式（31）所设计的政策变量控制器，可以使系统具有预期的动态性能，使得动态蒙代尔-弗莱明系统渐进稳定，实现对系统的控制目标。因此，仿真结果印证了定理3。上述过程的经济机制在于，通过式（31）所设计的政策变量使利率和汇率均保持在政府合理预期水平内。因此，投资和消费均保持相应的平稳增长，而不再剧烈波动和振荡，引致总产出平稳增长，从而使整个经济系统不再剧烈波动与失衡。仿真结果也表明，利用式（31）所设计的政策变量可以使开放经济条件下货币市场、产品市场和国际市场的供需水平趋于均衡，有效调整与控制开放经济系统的演化状态。

5 结语

蒙代尔-弗莱明模型是研究开放经济条件下财政政策和货币政策对宏观经济影响的重要工具。本文利用经济控制论方法建立蒙代尔-弗莱明模型的控制系统，在此基础上研究蒙代尔-弗莱明模型的动态结构特征，以及开放经济系统的控制律设计，得到蒙代尔-弗莱明模型控制系统的纯增益反馈控制律的解析解并进行仿真分析。研究表明：动态蒙代尔-弗莱明系统具有完全能观性、能控性和能达性等控制结构特征；可以任意配置动态蒙代尔-弗莱明模型闭环系统的极点，使系统渐进稳定，达到输出调节并具有满意的动态性能，仿真结果进一步验证了反馈控制律对蒙代尔-弗莱明系统控制的有效性。

本文研究结果证实，在现代西方经济学标准假设下，开放经济系统——蒙代尔-弗莱明模型具有可控性，即当开放经济系统出现较大波动时，可以采用适当财政政策、货币政策和汇率政策熨平经济系统波动，实现经济平稳快速发展。本文也为相关机构及决策者面对开放经济系统波动就宏观经济政策制定与经济系统分析提供了新的逻辑视角和理论支撑。