完井作业油管柱失效的力学机理——以塔里木盆地某高温高压井为例

杨向同 沈新普 王克林 沈国阳 耿海龙 邓 鹏

1.中国石油塔里木油田公司 2. 天津辰兴工程技术有限公司 3. Guoyang Technology and Services LLC, USA

0 引言

中国石油塔里木油田公司天然气开发中超深高温高压井的管柱力学问题在过去10年里受到若干研究者的关注[1-3]。3号井是1口高温高压超深油气直井，储层温度接近180 ℃，深度约7 000 m，储层孔隙压力接近120 MPa。在井筒排液测试期间，出现油套连通现象，起出管柱，发现油管柱在第418根和第432根发生了断裂。观察发现，最初的起始裂纹为疲劳裂纹。

油管柱位于井下承受静载荷，发生疲劳裂纹断裂的风险不大。3号井之所以能够发生疲劳裂纹断裂，是因为多方面的原因，主要有：①由于钻井质量不够好，实际井眼轨迹偏离设计轨迹，闭合距的偏离具有一定的震荡特点，从而当其中的油管通过这些位置时会有附加弯曲应力出现，造成局部应力在常规轴向力的基础上一定程度的应力震荡；②施工及生产过程中的温度变化明显，温度升降引起管柱伸长/收缩从而导致管柱反复通过局部应力震荡位置，导致应力的反复变化；③油管—套管之间的间隙设计不够合理，使得局部管柱有发生弯曲变形的空间，导致管柱发生应力震荡。

造成管柱侧向弯曲变形及扭转的载荷有两类，其中一类是施加在管柱轴向的载荷，包括力载荷与热载荷。这个载荷能导致管柱失稳、侧向弯曲及扭转，另一类是作用在管柱侧表面上的套管支反力载荷。因为井眼轨迹有水平延伸即横向位移，造成管柱下入井孔时支反力载荷致使管柱沿井眼轨迹的横向发生位移。管柱内部及外部的液体压力载荷及重力载荷一般不会直接导致管柱的横向位移。上述两类位移都是管柱弯曲及扭转变形的主要因素。当位移对应的应力足够大时，管柱将进一步发生塑性变形及断裂。

采用有限单元法进行管柱的三维力学数值分析是近年来的一个热点研究[4-6]。较之三维管柱力学解析解，其优点在于：①它可以模拟施工过程以及与施工过程相关的变形过程，从而得到与过程相关的局部应力变化；②对油管和套管之间的接触进行逐点分析，并根据接触情况得到相应的摩擦力大小。

Abaqus有限元软件提供了套管—油管接触单元（以下简称ITT），并且根据厚壁筒受内压—外压的理论，提供了管截面上24个点的应力解析解，这样就在保证位移和应力数值解精度的前提下极大地提高了管柱计算求解效率。

笔者通过建立管柱的三维有限元模型，分析管柱的力学行为，在应力分析数值解的基础上，分析管柱关键部位的疲劳强度安全系数。

由于管柱同一深度截面上的位移只有一个值，在管柱分析数值结果中，笔者把下封隔器坐封作业、压裂作业、测试作业共3个作业的位移解一起放在同一个图中以比较的形式展示。由于管柱同一深度截面上的应力点有24个，我们在每个深度的截面上挑出了9个点的应力值进行应力结果展示。

笔者分析模拟了下封隔器坐封、压裂、测试作业3个工况的管柱系统的位移和应力。由于测试作业的管柱所受的温度载荷及压力载荷都比较大，因此在结果展示时首先展示测试作业的位移和应力数值解，之后再展示坐封和压裂两个作业的管柱位移和数值解。

在分析疲劳强度安全系数时，笔者采用了本文参考文献[7-8]中的疲劳强度理论模型。

1 输入数据

1.1 井眼轨迹的信息

为了展示钻井质量不佳引起的井眼轨迹的闭合距震荡变化，图1给出了3号井井眼轨迹闭合距随深度变化的曲线。在4 000 m以下井深，有10个主要的不规则横向闭合距震荡区段。

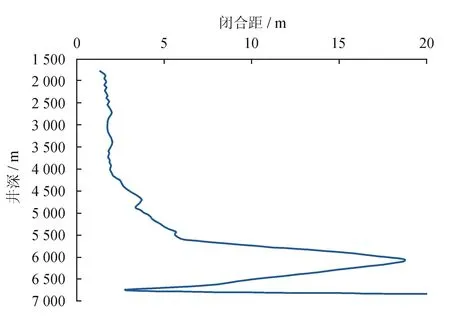
图1 井眼轨迹闭合距偏离设计轨迹的信息图

1.2 3号井管柱疲劳裂纹断裂情况

3号井管柱疲劳裂纹断裂的具体情况为第418根油管（垂深4 146 m）、第432根油管（垂深4 285.39 m）工厂端丝扣根部断。断口如图2所示。观察发现，第418根油管接箍完好无损，丝扣/公螺纹在与接箍连接的根部断裂。第432根油管丝扣断裂位置与第418根油管类似。

图2 油管断口照片

1.3 油管柱机械参数

油管柱的几何尺寸、油套间隙的机械参数见表1。

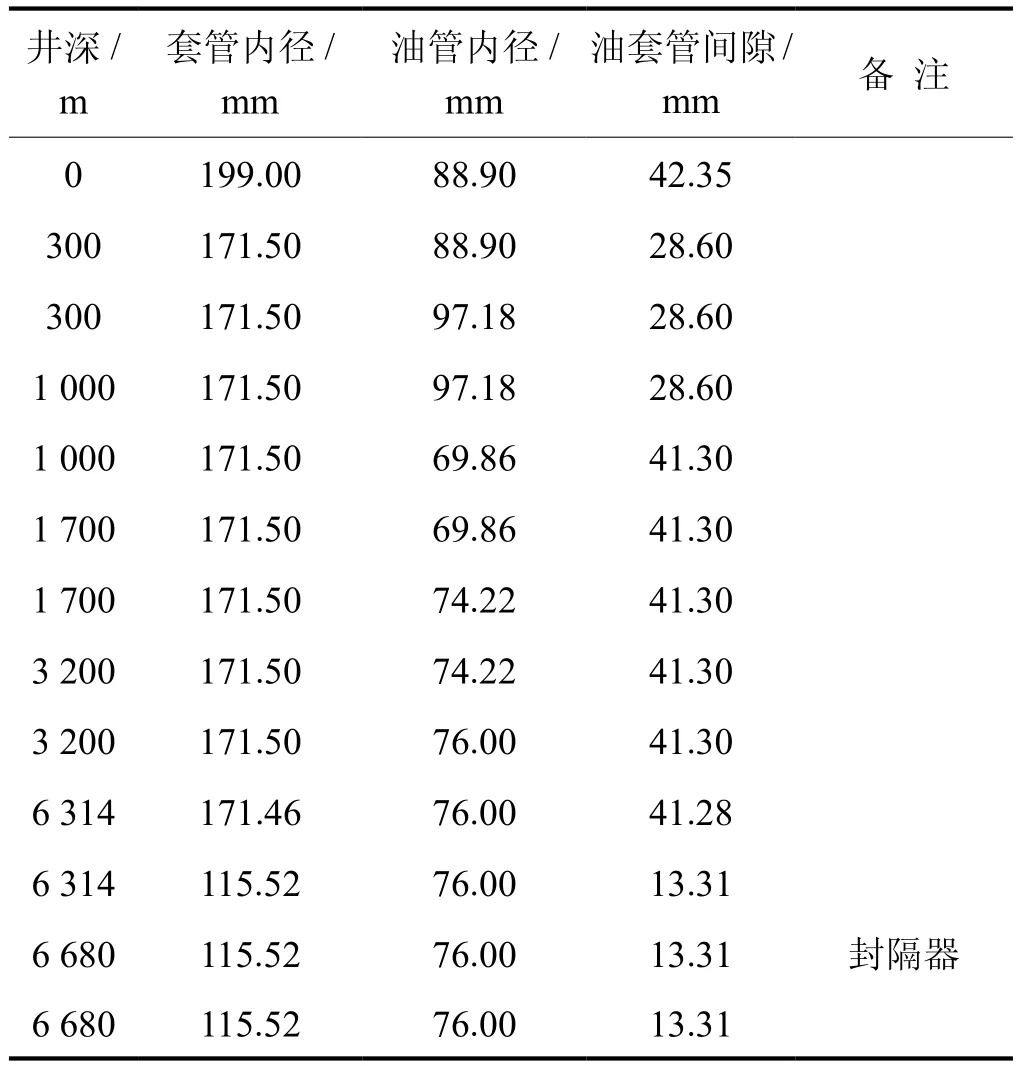
表1 油管柱的参数及油套管间隙表

2 三维管柱有限元模型及载荷

采用上述数据，建立管柱三维有限元模型并进行分析。图3给出了管柱的6 810 m全长示意图。模型采用2 123个二次管单元pipe32H、4 247个节点模拟油管。图3中的坐标原点位于井口，纵向为z轴，两个水平方向分别为x轴和y轴。闭合距偏离在模型中为沿x轴方向的偏离。模型自顶端开始至封隔器处设置了ITT接触单元。封隔器以下的管柱部分不是分析的重点，为减少计算工作量，封隔器以下部分管柱没有设置ITT管—管接触单元，仅设置了pipe32H管单元模拟这部分管柱。

图3 管柱模型示意图

管单元按厚壁筒计算，在管截面上的应力点共有24个点，如图3所示。下述的9个应力点均在这24个点中选出。

管柱材料力学性能如表2所示，包括管柱材料的刚度、强度、密度和热膨胀参数。坐封、压裂、测试作业时的压力载荷参数如表3所示。

目标井管柱在不同工况的温度分布参数见图4。

表2 管柱材料力学性能表

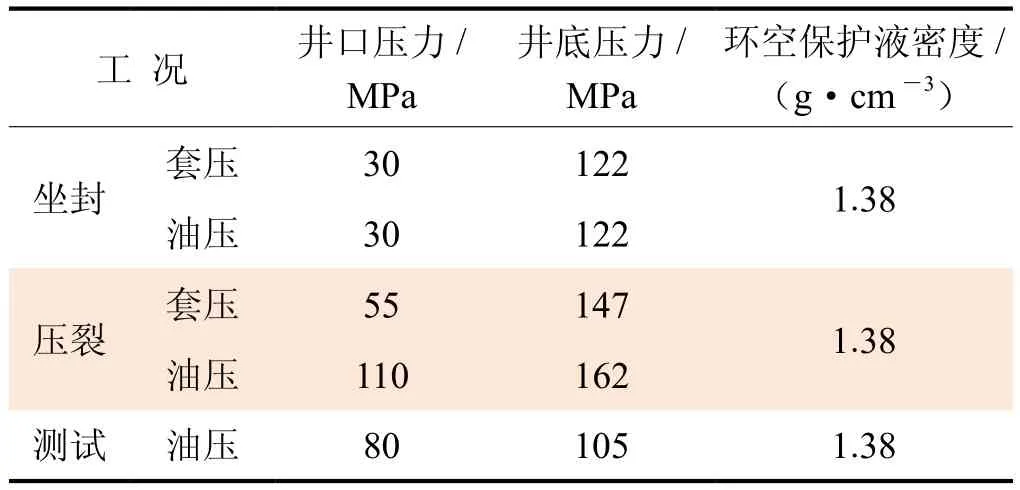
表3 压力载荷参数表

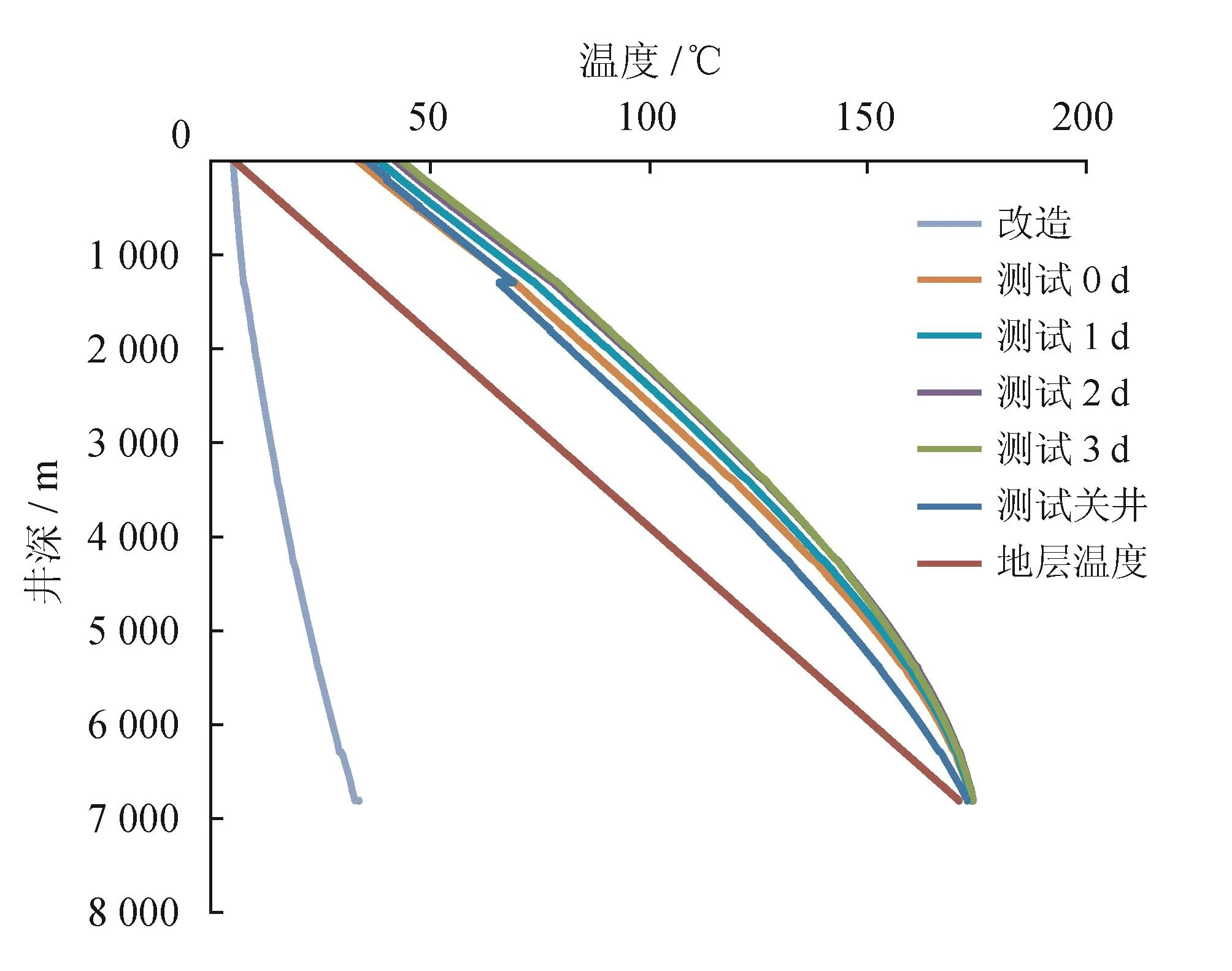
图4 不同工况下管柱温度分布图

3 Abaqus有限元管柱三维变形及应力分析数值结果

3.1 x方向管柱位移比较与分析

图5显示了完井的3个作业（封隔器坐封、压裂、测试）的管柱沿水平面x方向的管柱位移（ux）分布图。

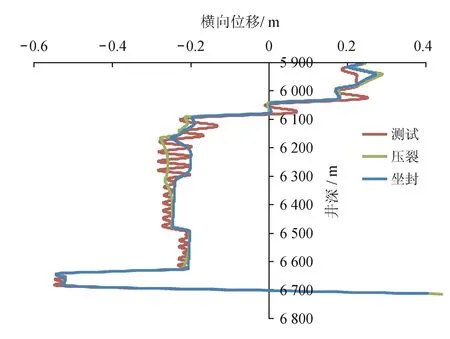
图5 作业期间管柱变形分布图

由图5可知，测试作业时在下部管柱（5 900 m以下）横向位移的变形因素开始明显，管柱局部屈曲失稳造成的横向变形周期型震荡，而压裂阶段和坐封前阶段没有屈曲失稳震荡现象。

3.2 y方向管柱位移比较与分析

图6为完井作业时管柱螺旋形失稳变形时沿水平面y轴的位移（uy）局部放大图。由图6可知，上部的油套间隙约为0.043 m，下部约为0.013 m。上部一个波长跨度在井深6 262～6 293 m，长度（或距离）为31 m，跨越逾3根油管长度；而下部的波长跨度在井深6 323～6 351 m，长度为29 m，跨越近3根油管长度。

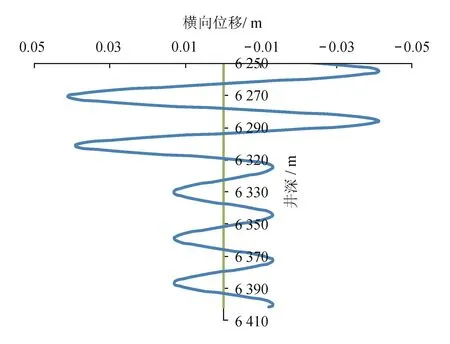
图6 完井作业时管柱螺旋形失稳变形的局部放大图

3个作业管柱沿z轴的轴向位移（uz）见图7。

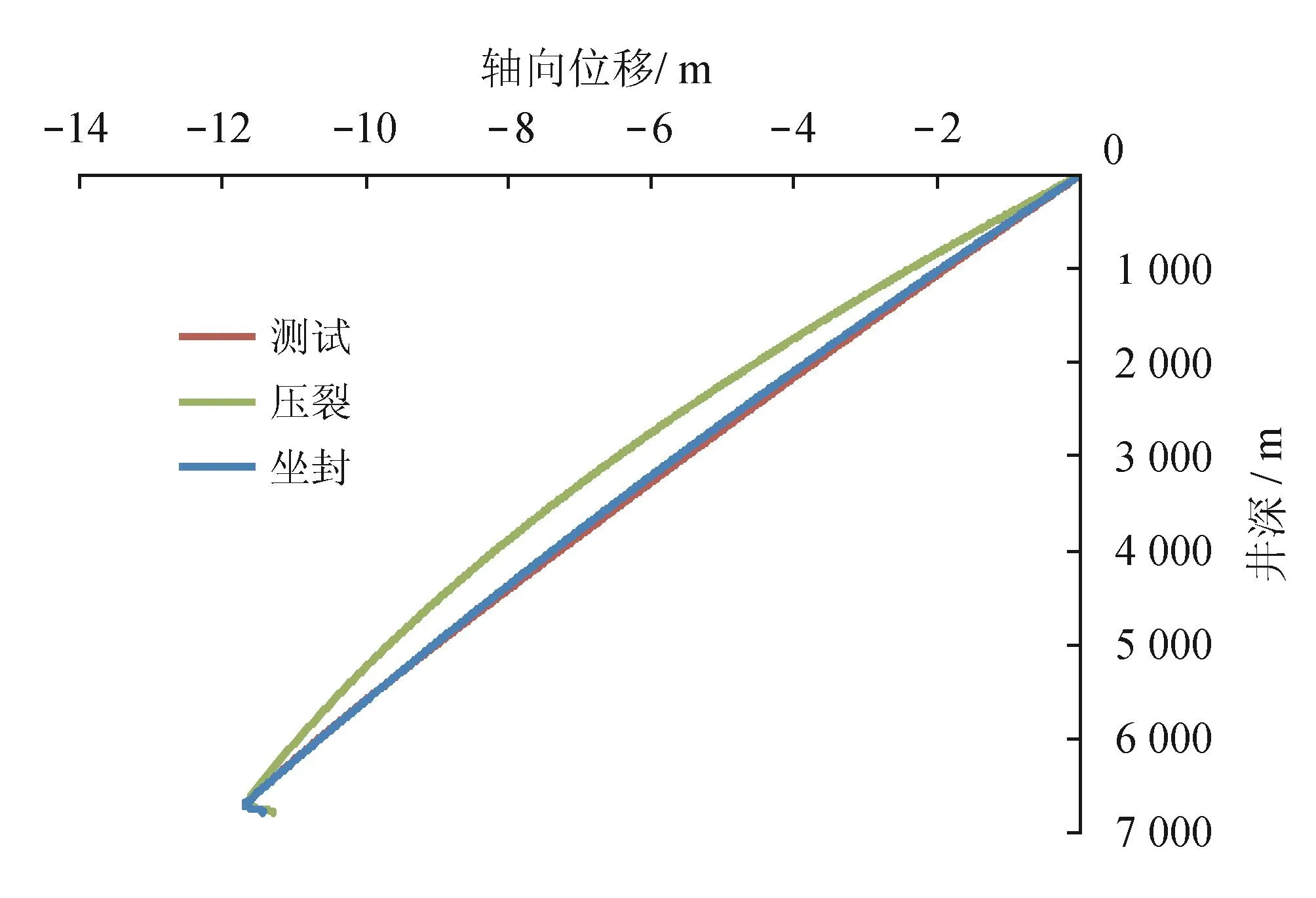
图7 3个作业管柱的轴向位移分布比较图

由图7可知，轴向位移初始值和完井作业时的差别不大。压裂作业时因为温度降低引起管柱收缩，中间深度上的管柱的轴向位移值有一定减小。封隔器处的轴向位移发生在坐封之前。坐封之后封隔器处的轴向位移增量为零。

3.3 测试作业时管截面上的各点应力分析

如图8-a所示，模型输出应力时选用的厚壁圆管的截面上的点沿圆周的分布及编号。第1至9号点为套管上的点，这里的是油管柱上截面的点。第12和13号点都在1轴上。分别位于外圆周及壁厚中间。其他7点都在外圆周上。图8-b给出了管柱横截面上第10至第18共9个点上的轴向应力分量（s11）值在不同深度的管柱上分布。图8中看出，同一深度的横截面9个点上的s11值很接近。

图9为图8-b分别截取6 100～6 800 m及4 100～4 300 m两个井段的放大图，截面上9个点的s11分布及比较。由图9-a可知，在6 100～6 300 m深度间隔上的截面内9个点间的s11差为32 MPa。单点的最大变化幅度为其1/2，即16 MPa。在6 300～6 600 m深度间隔上的截面内s11差为20 MPa。油层套管大间隙和小间隙之间的截面内s11差约为12 MPa。应力变化幅值为其1/2，即分别为10 MPa和6 MPa。由图9-b可知，在4 100～4 300 m深度间隔上，通过同一深度上红蓝两条s11曲线的比较可以得出：弯曲引起的截面内的s11差为157－144 = 13 MPa。单点的应力变化幅值为其1/2，即6.5 MPa。数值计算结果还显示：由于弯曲变形等原因，位于壁厚中间点的截面点12位置上的sMises和环向应力分量（s22）明显比位于外圆周上的其他8个点上的值都大。

3.4 坐封作业时管截面上的各点应力分析

表4给出了下管柱坐封、压裂和测试作业管柱的轴向应力波动的应力变幅及平均应力。

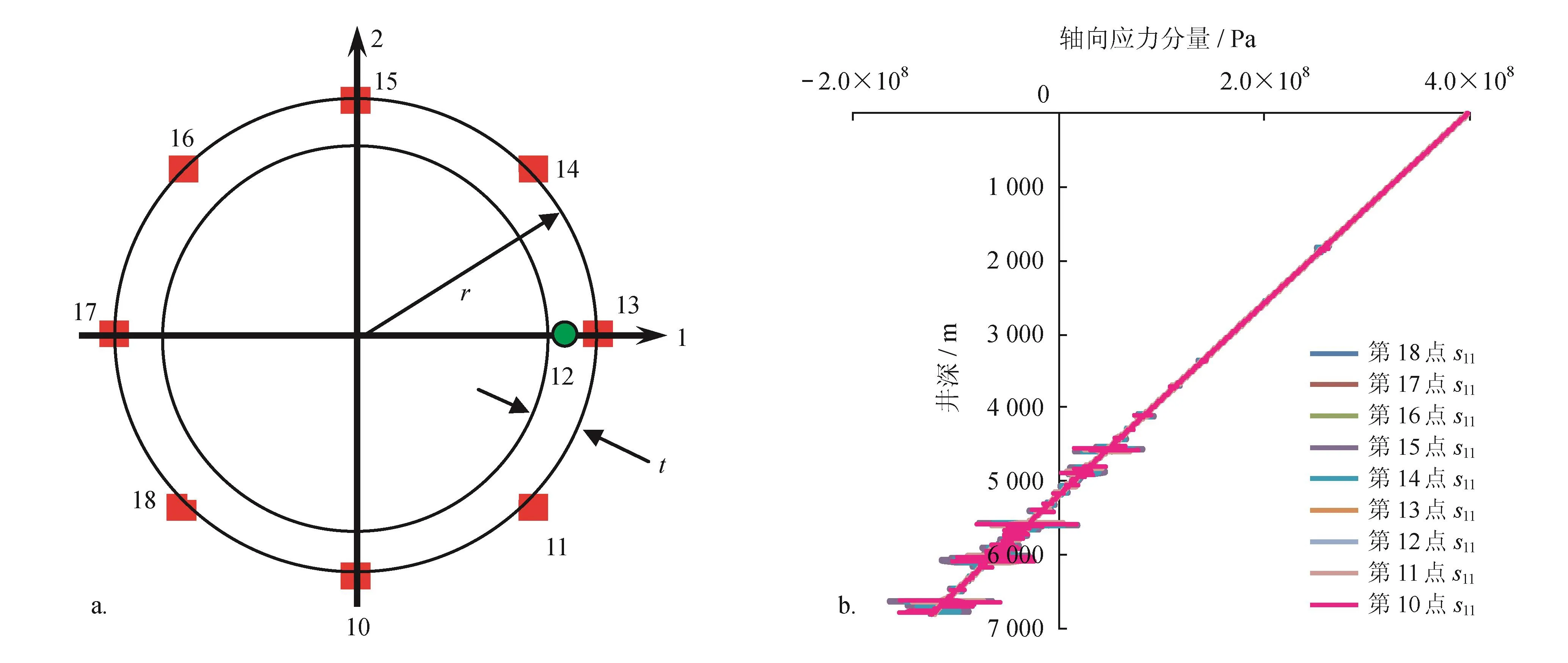
图8 坐封前不同深度处的管柱横截面各点轴向应力分量（s11）分布图

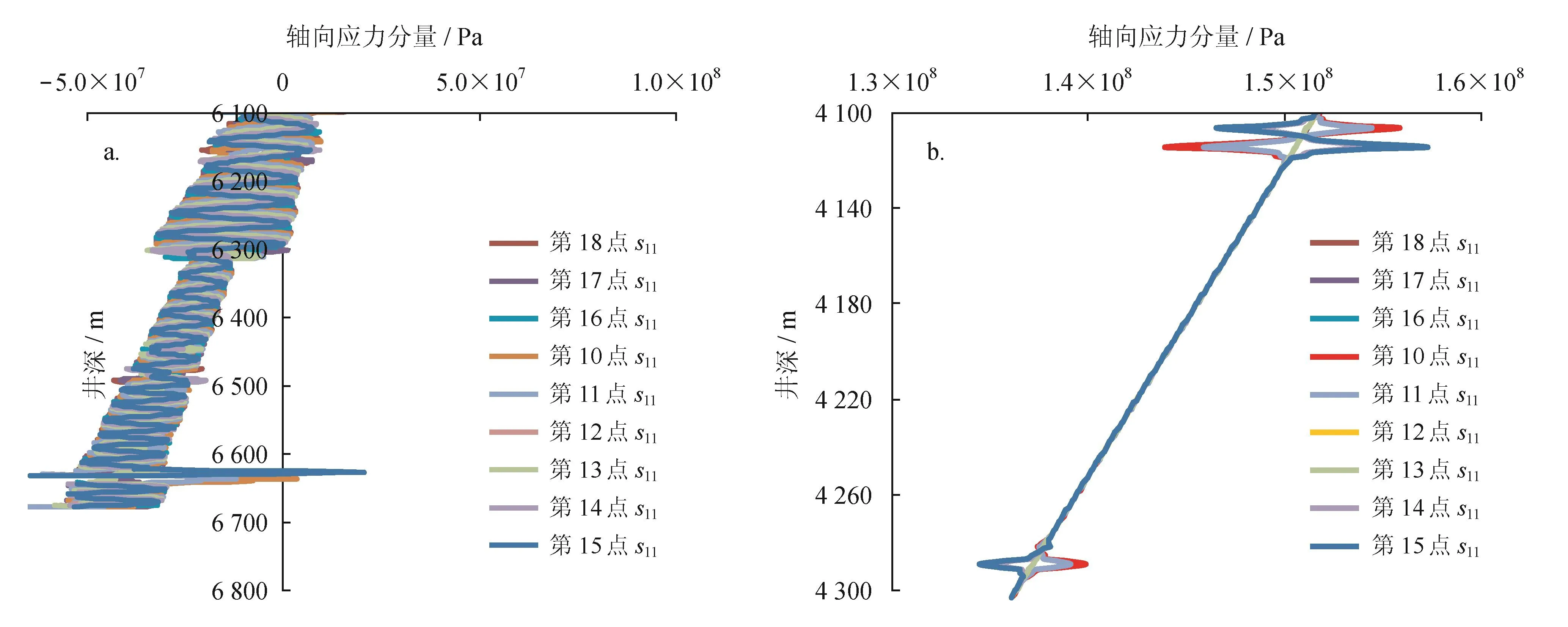
图9 不同深度管柱截面上9个点的s11分布及比较图

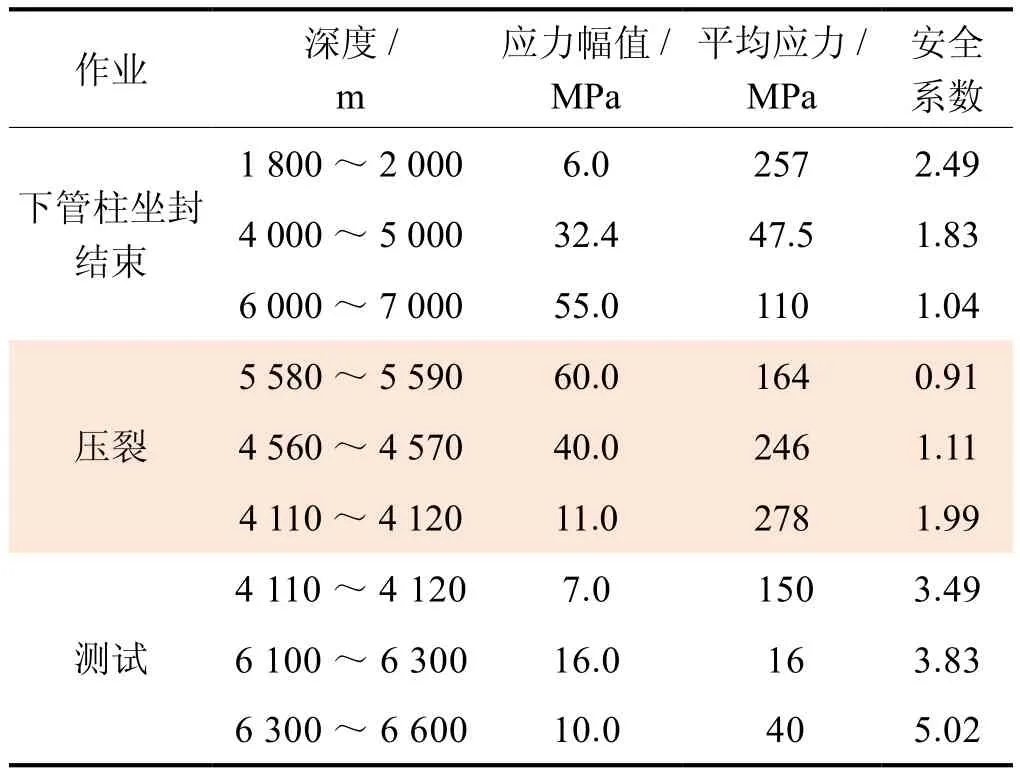
表4 完井作业的管柱轴向应力波动、平均应力及疲劳安全系数表

在下管柱作业坐封时，管柱的受力为重力、内压、外压以及底部的液体压力即浮力。数值结果显示：此时中和点的位置在5 294 m。在1 840 m深度上最大的应力变化幅度为6 MPa，此处的平均应力为257 MPa。在4 600 m深度上最大的应力变化幅度为32.4 MPa，此处的平均应力为47.5 MPa。在6 639 m深度上最大的应力变化幅度为55.0 MPa，此处的平均应力为110 MPa（表4）。

3.5 压裂作业时管截面上的各点应力分析

数值结果显示：此时管柱封隔器以上都进入处于压缩应力状态。压裂时管柱截面上各点的sMises等效应力的震荡现象明显，振幅在6 074 m深度上达到40.0 MPa。轴向应力分量（s11）在深度5 580 m和5 590 m上有一个弯曲引起的增量变化。增量幅值为60.0 MPa。轴向应力分量（s11）在深度4 110 m和4 120 m的管柱上有一个弯曲引起的增量变化。应力增量幅值为11.0 MPa，此处的平均应力为278 MPa（表4）。轴向应力分量（s11）在深度4 280 m和4 300 m局部弯曲亦引起的应力增量变化。应力震荡现象数值计算结果与观测现象很接近，但不是精确相同：两者之间的位置坐标有一定差别。这个差别的来源是管柱数值模型在对偏离“理想竖直的”井轨迹实际坐标点的几何信息做了近似处理。在近似处理过程中井孔轴线螺旋变化形式的偏离信息有所丢失。这些因素的共同作用导致数值解与实际现象的偏差。

3.6 疲劳强度计算法

在3号井油管柱分析中，交变应力的来源主要有2种：①由温度变化引起的热膨胀/收缩导致管柱位移。在局部发生弯曲变形时产生局部弯曲应力变化震荡。这主要发生在压裂及测试作业。主要表现为轴向应力分量（s11）的变化。②坐封下管柱过程中受到井眼轨迹约束强制变形引起的交变应力。管柱下入井孔套管的过程是一个动态过程，每当有管柱节通过井孔弯曲点时，弯曲导致的应力震荡变化就会出现。

根据文献[7-8]的理论，当前应力点的疲劳失效安全系数为：

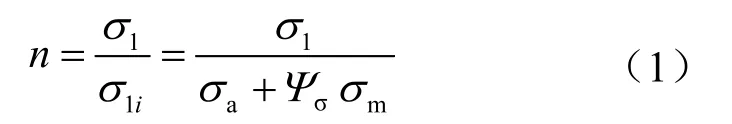
式中n表示疲劳失效安全系数；σ1表示疲劳极限，MPa；σ1i表示等效交变应力，MPa；σa表示应力变幅，MPa；σm表示平均应力，MPa；Ψσ表示应力不对称系数。

考虑结构的有效应力集中系数Kσ、尺寸系数ε、表面加工系数β三方面的因素对疲劳极限的影响之后，得到疲劳强度安全系数公式：

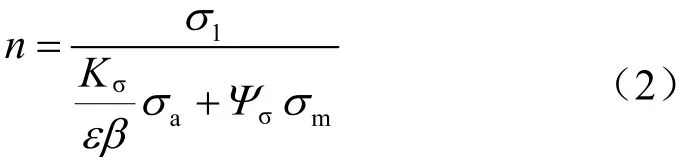
式（2）适用于拉压弯曲单向应力安全系数的计算。

3.6.1 应力集中系数的确定

应力集中系数（Kσ）的定义是结构截面上实际发生的最大应力与结构此处的名义应力之间的比值。参考文献中关于应力集中系数的描述很多，典型的与本项目相关的资料有：

1）螺纹处的应力集中系数根据材料强度高低，Kσ值可以从抗拉强度（σb）为350 MPa时的3变化到σb为890 MPa时的5.2。

2）变截面轴在截面台阶处的Kσ值的大小与台阶处的元角半径R、以及台阶的大小、截面两侧的轴半径之比有关，Kσ值从R为0时的5变化到R为0.3 d时的1.5。

综合考虑各种因素，取工厂端丝扣根部的应力集中系数为3.5。

3.6.2 尺寸系数、表面加工系数的确定

尺寸系数（ε）、表面加工系数（β）均取为1。

3.6.3 疲劳强度安全系数公式

将上述有效应力集中系数、尺寸系数、表面加工系数三方面的取值带入到疲劳强度安全系数公式（1）中，根据本文参考文献[8-9]，这里取不对称系数Ψσ为0.28，则

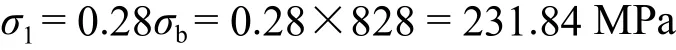
得到安全系数计算公式：

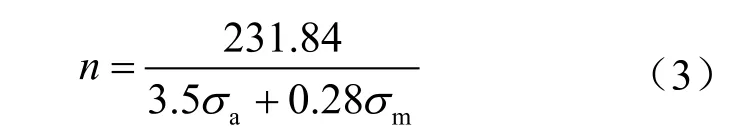
3.6.4 疲劳强度安全系数值

由上述计算模型对参数取值：应力集中系数为3.5，尺寸及表面质量系数取1，不对称系数为0.28，抗拉强度为828 MPa，疲劳极限为231.84 MPa，采用表4的应力值，使用式(3)计算得到各弯曲应力部位的疲劳安全系数值（表4）。由表4可看出：

1）压裂作业，在深度5 580～5 590 m，疲劳安全系数n值小于1，标为红色警告区。在深度4 110～4 120 m和4 560～4 570 m，n值分别为1.99和1.11，n值大于1、小于2，标为黄色预警区。在其他管段的安全系数n值大于1.99，属于绿色安全区。

2）测试作业，各段的安全系数都大于3，安全，标为绿色安全区。

3）下管柱结束，坐封，在1 840 m深度上有应力波动区，n值为2.49，属于绿色安全区。在4 590～4 610 m和6 629～6 649 m深度上有应力波动区，n值分别为1.83和1.04，属于黄色预警区。

4）模型中忽略了深度1 800～2 600 m井眼轨迹方位角变化可能产生的支反力/扭转载荷作用。

5）在第418根和432根油管断裂的深度4 100～ 4 300 m的管段，靠近安全系数黄色预警区。

4 结论与建议

笔者针对3号井的实际工程问题建立了三维有限元管柱力学模型及疲劳安全系数的计算公式，弯曲应力部位疲劳安全系数值计算结果表明：

1）测试作业各油管段的安全系数都大于3，属于安全状态。

2）断裂的2段油管疲劳安全系数值分别为1.99和1.11，处于预警区。其他管段的安全系数大于1.99，属于安全区。

3）模型中忽略了深度1 800～2 600 m之间井眼轨迹方位角变化可能产生的支反力/扭转载荷作用。这使得计算所得疲劳安全系数的结果比实际上的可能值要大，实际的安全系数要小于计算值。

结合管柱应力分析数值和疲劳安全系数分析结果，为了保证管柱的完整性、保障安全生产，建议：

1）对管柱安全系数较低、黄色及红色失效风险较大的管段，有必要在下管柱/安装前采取措施降低应力集中系数，比如增大螺纹接箍部位的圆角等。

2）提高材料的强度极限。