化肥对中国粮食产量变化贡献率的研究

麻 坤，刁 钢

（1 河北科技大学经济管理学院，河北石家庄 050061；2 河北农业大学商学院，河北保定 071000）

已有研究证实化肥与中国粮食产量的增加存在正相关关系。鲍先琬[6]利用灰色关联方法计算中国化肥用量与粮食产量的关联系数，发现两者有较高的关联程度，周慧秋[11]利用同样的方法计算东北地区粮食产量影响因子，结果表明化肥施用量对粮食产量有正向影响，其影响程度仅次于播种面积和有效灌溉面积。谢杰[12]利用中国1978—2004年间的统计数据，通过逐步回归和加权最小二乘回归方法，构建了线性粮食生产函数，回归结果表明土地和化肥投入是影响粮食生产的最主要因素，均对粮食产量产生正向影响。

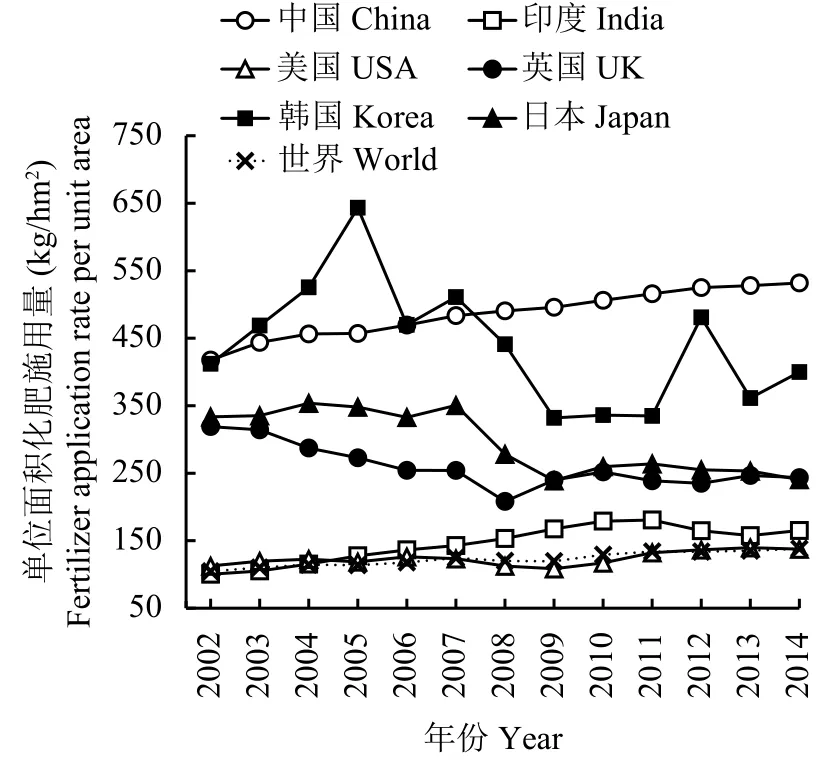
图1 主要国家单位面积化肥施用量Fig.1 Fertilizer application rate in main countries[数据来源于世界银行数据 Data from World bank data 2017]

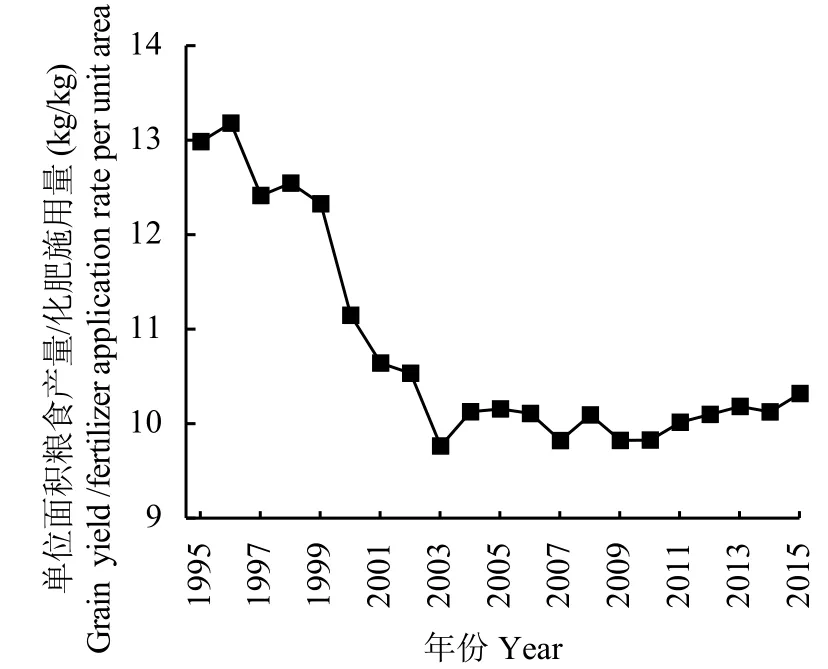
图2 中国单位面积产量/化肥施用量Fig.2 Yield/fertilizer application rate per unit area in China[数据来源于世界银行数据 Data from World bank data 2017]

施用化肥的确可以补充土壤养分供给，促进作物产量的增加。然而根据经济学的边际报酬递减理论，随着单位土地面积化肥投入量的不断增加，化肥投入对粮食增产的贡献率会逐渐下降。尹世久等[13]对比中国四个时期跨度的粮食产量与其主要影响因素的灰色关联系数，发现化肥与粮食产量的关联度由大变小。李红莉等[14]利用调研数据，分析了不同粮食作物化肥施用量和效率的变化，结果发现玉米的化肥施用量增加，但增产效率却下降。Cerrato等[15]、Bélanger等[16]分别利用试验数据对比了几种不同的产量反应模型，结果发现二项式方程对产量和化肥施用量的关系描述更为准确。张峰等[17]借鉴了该模型，利用1990—2008年间粮食产量与化肥施用量的统计数据估计了粮食生产的二项式函数模型，验证了二者之间存在经济学意义上的倒U型关系，即随着化肥施用量的增加，粮食产量增加速度逐渐放缓。

二项式生产函数一般仅考虑化肥一项投入要素对产量的影响，但根据前人研究，粮食产量除了受化肥影响之外，还受土地、灌溉面积等其他投入要素的影响。为了更准确地描述粮食产量和化肥投入量的关系，需在粮食生产函数模型中纳入其他变量。柯布道格拉斯生产函数 (C-D函数) 可以综合考虑多个生产要素对于产量的影响，并且其估计结果可以直接获得不同要素的弹性系数，故被经济学家大量引用。王祖力等[7]选取粮食播种面积、粮食成灾面积、劳动投入、化肥投入、其他物质投入等指标，利用1978—2006年的数据估计了C-D形式的粮食生产函数，结果显示化肥弹性系数为0.2；由于化肥投入量与播种面积可能存在共线性问题，影响模型估计结果，黄季焜等[18]选用单位面积投入产出数据来克服这一问题，其研究结果显示北方水稻单产对化肥投入弹性系数为0.208，南方的化肥弹性系数为0.098，南北方化肥投入弹性系数差距较大，粮食生产的地区差异不容忽视；除以上因素以外，魏津瑜等[19]考虑到农业技术投入和基础设施建设对粮食增产的影响，将农业机械总动力、有效灌溉面积纳入总产量模型，得出化肥弹性系数为0.39；吴英杰等[20]则考虑了国家政策对粮食产量的影响，将净农支出变量引入模型，其估计的化肥弹性系数为0.51。对比以上研究结论可以发现，由于研究时间、区域、数据来源和研究方法的不同，化肥对粮食产量影响程度的估计结果也不尽相同。鲍先琬[6]、周慧秋[11]的研究认为粮食产量与化肥施用量关联程度高，但是尹世久等[13]的结果却说明化肥与粮食产量的关联度已下降。魏津瑜等[19]、吴英杰等[20]估计的化肥投入总量的弹性系数较高，而王祖力等[7]估计的系数偏低。

已有研究侧重分析粮食产量与化肥投入量及其它因素的关系，主要运用全国粮食投入产出的时间序列数据估计二项式或C-D函数形式的粮食生产函数，通过化肥系数来描述化肥对粮食产量的静态影响。然而不同省份粮食生产力存在差异，并且化肥对粮食产量变化的贡献率是动态变化的。张立庠等[21]将不同省份粮食生产力的差异性纳入模型构建中，并将1952—2006年全国30个省份的面板数据分成5个不同时期，采用固定效应模型对不同时期的粮食总产量对化肥施用量的弹性系数动态变化进行分析，发现化肥弹性系数呈倒U型趋势。但固定效应模型假定每个省份的差异不随时间变化而变化，这与粮食生产力不断发展的实际情况并不相符。本研究利用1995—2015年的粮食投入产出的省际面板数据，分别估计了C-D生产函数和二项式两种形式粮食生产函数的混合效应、固定效应和随机效应模型，并对模型进行了验证，选择最优模型，然后根据模型估计结果计算了化肥施用量的不变弹性和可变弹性，以及化肥对粮食的增产贡献率，通过对比不同指标值及其变化趋势，明确目前化肥投入对粮食产量的实际影响。

1 材料来源与研究方法

1.1 材料来源

本研究收集了1995—2015年中国30个省份 (含直辖市) 的粮食总产量、化肥施用量、农机动力、有效灌溉面积比例、成灾面积比例数据，数据来自万德数据库 (2017) 和《中国统计年鉴》。由于统计数据并未将粮食与其他农作物生产的单位面积农机动力、灌溉面积和成灾面积的数据加以区分，并且我国的粮食播种面积占农作物总播种面积的60%以上，故本研究采用统计年鉴中农作物的投入数据来代替粮食生产投入数据。

1.2 研究方法

1.2.1 粮食生产函数模型 柯布道格拉斯生产函数是美国数学家柯布 (Cobb C W) 和经济学家保罗·道格拉斯 (Paul H Douglas) 探讨投入和产出关系时创造的生产函数 (公式1)，该生产函数综合考虑了资本、劳动力和技术等多种要素对产出的影响，是经济学中使用最广泛的一种生产函数形式。将该函数公式两边取对数，可以将其转化为线性回归模型 (公式2)。CD模型估计的化肥弹性系数是固定不变的，而以往的研究结论显示化肥投入存在边际报酬递减趋势，其弹性系数会在不同时期发生变化，利用二项式生产函数模型 (公式3) 可以计算出化肥的可变弹性系数。为了对比化肥施用量对粮食产量的静态和动态影响，本研究分别估计了这两种形式的粮食生产函数模型。

柯布道格拉斯粮食生产函数 (模型1)：

2.问题的设置要有一定的启发性。教师在进行问题设置时必须注意其启发性，学生在思考的时候便会有一定的疑惑，这样很容易让学生为了问题进行争论，这样，学生的交流也会增多，学生的思维也很容易得到开发，比如说教师在教学时，设置问题启发学生进行思考，并对学生进行一定引导，这样学生在思考问题时，便会愿意更加积极地进行探索，从而不断提高自身的思维创造力和探究性思维。教师在设置问题时，应该设置一些灵活性比较强的题目，并对学生进行启发，教会学生举一反三，这样学生的思维会更加灵活，很容易学会一类题的解法。

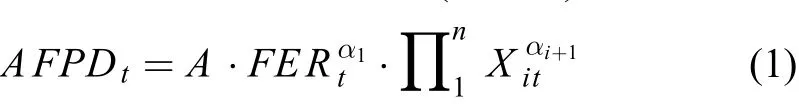
公式1取自然对数：

二项式粮食生产函数 (模型2)：

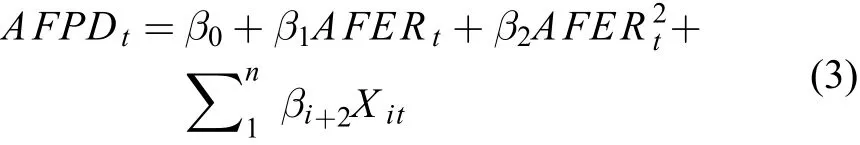
式中：t表示时间；AFPD表示单位面积粮食产量；AFER表示单位面积化肥施用量；X表示除化肥以外其他影响粮食产量的因素。

1.2.2 混合效应、固定效应和随机效应模型 考虑到各省粮食生产的异质性，本研究选用面板数据来估计全国粮食生产函数。利用面板数据进行模型估计时，会涉及面板数据回归模型的选择问题。面板数据回归模型主要包含三类：混合效应模型、固定效应模型和随机效应模型。混合效应模型假定各省粮食生产不存在差异，直接将所有数据进行混合，然后再进行估计，这样的估计结果不能反映出不同省份之间的生产力差异对全国粮食生产函数的影响；固定效应模型考虑了各省粮食生产的差异，但假定这种差异是固定的，不随时间变化而变化；而随机效应模型则假定各省粮食生产力的差异是随机变化的。

对于模型选择方面，不同学者相继给出若干判断标准。本研究主要利用Eviews软件中的固定效应和随机效应两种检验方法来选定模型。固定效应检验的原假设是固定效应模型优于混合效应模型，主要依据F统计量的显著性来判定。如果F统计量显著，则接受原假设；反之，则拒绝原假设。随机效应检验的原假设是随机效应模型优于固定效应模型，主要依据χ2统计量的显著性来判定。如果χ2统计量显著，则接受原假设；反之，则拒绝原假设。

1.2.3 粮食生产函数模型变量选择 本研究主要分析单位面积粮食产量和化肥施用量的关系，已有部分研究只分析化肥投入一个变量对粮食产量的影响，但粮食产量受多种因素影响，除了化肥之外，土地和农业基础设施等资本投入要素、劳动力要素、技术要素投入也是影响粮食总产量的重要因素。基于已有针对粮食产量影响因素的研究结论和成果，本研究在模型中引入了四个控制变量：有效灌溉面积比例、粮食成灾面积比例、单位面积农业劳动力、单位面积农机总动力。但是由于我国的农业劳动力并不是完全从事粮食生产，利用农业劳动力数量作为粮食生产劳动力数量的替代变量效果较差，所以在模型中剔除了单位面积农业劳动力这一变量。根据已有研究成果，公式2中化肥施用量的系数代表化肥施用量弹性，符号预期为正，表示化肥施用量变化1%引起的粮食产量变化的百分比；公式3中，化肥施用量一次项的预期系数为正，二次项的系数预期为负。农机总动力和灌溉面积与粮食产量之间的关系预期是正相关的，成灾面积与粮食产量的关系预期是负相关的 (表1)。

2 模型估计结果及化肥对粮食产量变化的贡献率分析

2.1 粮食生产函数模型的估计结果分析

本研究利用Eviews9.0分别计算了公式1和2两种形式的混合效应、固定效应和随机效应模型。由于面板数据可能存在异方差和序列相关问题而导致系数显著性检验结果不可靠，故回归结果的标准差采用了面板修正 (PCSE) 标准差以修正这种偏误。固定效应检验的F统计量值分别为91.67 (模型1) 和95.88 (模型2)，高度显著，故判定固定效应模型优于混合效应模型。随机效应检验采用豪斯曼检验方法，模型1和2的χ2值为0，概率为1，高度显著，故判定随机效应模型优于固定效应模型。两个模型的回归结果基本符合假设，且与已有研究较为一致(表2)。化肥施用量系数符号与预期一致，且显著性水平较高，表明化肥对单位面积粮食产量增加有正向影响，模型2中化肥二次项系数显著为负，表明化肥投入对产量的影响符合倒“U”趋势；两种函数形式的随机效应模型估计结果显示，有效灌溉面积比例的系数与假设相反且不显著，这可能是由于有效灌溉面积数据包含非粮食作物面积，所以灌溉面积对单位面积粮食产量增加的效果不明显；两个模型中成灾面积比例系数都是统计显著的，符号均为负，说明成灾面积对单位面积粮食产量有明显的负面作用；两个模型的单位面积农机总动力系数高度显著，但相比化肥系数而言数值较小，说明在现有的土地政策下农业机械化虽然在粮食增产方面发挥了一定作用，但作用仍不明显。农业机械化程度和成灾面积是粮食生产中的技术要素投入，模型结果说明目前技术要素在粮食增产中的作用仍不及化肥。

表1 模型中变量的基本情况Table1 Variables in the model

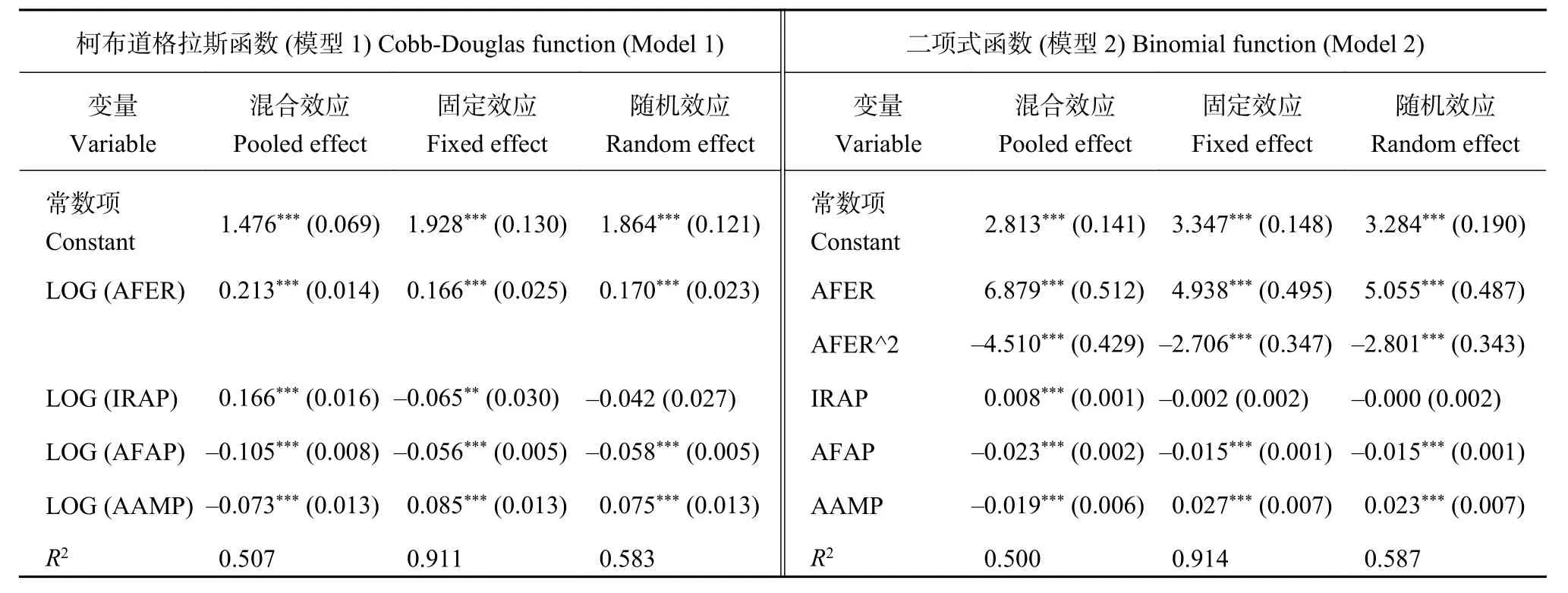
表2 模型回归结果Table2 Model results

2.2 化肥施用量弹性及其对粮食产量变化的贡献率分析

已有研究主要通过关联系数、粮食生产函数中的化肥系数和化肥弹性系数来判断化肥对粮食产量的影响。关联系数只能说明粮食产量和化肥投入之间关系的紧密程度，并不能说明化肥投入对粮食产量的具体影响；粮食生产函数中的化肥系数的符号和大小代表化肥对粮食产量的影响方向和程度，但不同形式的方程估计的系数会有差异；化肥投入的弹性系数是指每增加1%的化肥投入带来的粮食产量增加的百分比，描述的是化肥变化率与粮食产量变化率的关系，反映的是比例关系，不能反映增量的变化；化肥贡献率则借鉴了全要素生产率的概念，指在粮食产量增加中化肥贡献的百分比，化肥贡献率可利用化肥投入弹性乘以化肥施用量变动的百分比计算获得，该指标剥离了其他因素对产量增加的影响，更能直观说明化肥对粮食产量变化的影响。故本文利用C-D和二项式的随机效应模型回归结果求解了化肥施用量的弹性，并计算化肥施用量对粮食产量的贡献率，以此来分析不同时期化肥施用量对粮食产量变化的实际影响。

1) 柯布道格拉斯生产函数形式

将公式2两边分别对AFER求一阶导数，

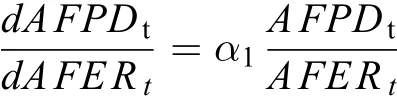
则化肥施用量弹性为：

2) 二项式生产函数形式

将公式3两边分别对AFER求导数，

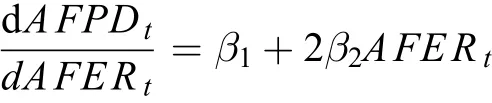
则化肥施用量的弹性为：

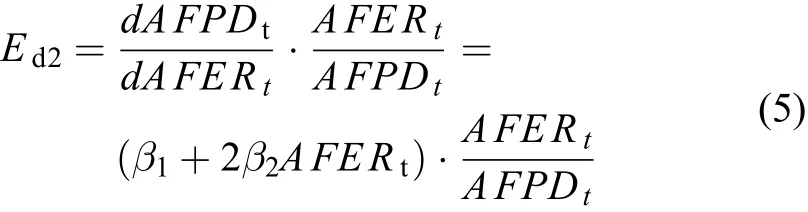
3) 化肥对粮食增产的贡献率

将公式1两边全微分，可发现各要素对粮食产量变化的贡献率：

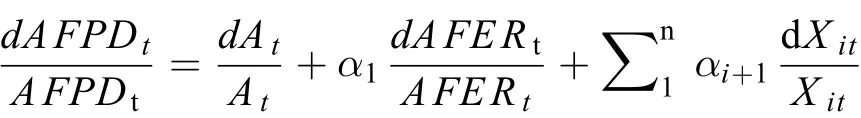
因此，化肥对粮食增产的贡献率 =

依据公式4和5，结合随机效应模型回归结果，分别求解出化肥施用量的弹性；根据公式6，结合公式4和5的结果，可以计算出化肥施用量在粮食增产中的贡献率。模型1估计的化肥弹性系数是固定值0.17；模型2估计的化肥弹性系数是可变的，图3描述了单位面积粮食产量对化肥施用量的弹性系数的变化趋势，可以发现化肥施用量弹性系数的变化符合倒“U”型曲线，该弹性系数在2000年左右达到最大值，2000年以后开始呈现出明显下降的趋势。这说明化肥投入已经超过了经济学的最优施用量，进入边际报酬递减阶段，在其他要素投入相对稳定的情况下，再增加化肥施用量并不能带来预期的产量增加，反而会增加生产成本、污染农业生产环境。

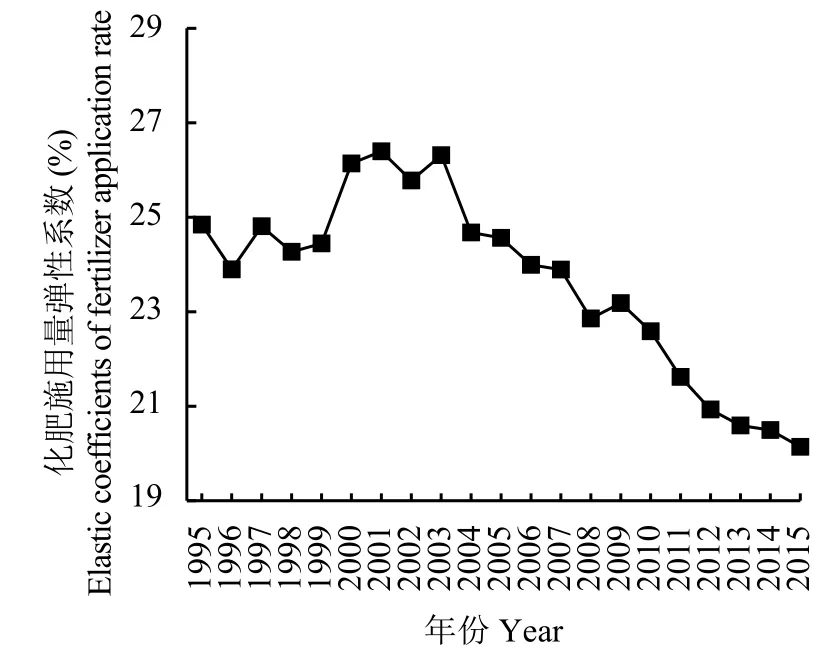
图3 模型2估算的粮食产量对化肥施用量的弹性系数Fig.3 Elasticity coefficients of grain yield to fertilizer application rate estimated with Model 2

图4 描述了单位面积粮食产量变化率以及模型1和2的化肥施用量对单位面积粮食产量变化的贡献率。其中，模型1的贡献率由公式4的弹性Ed1与化肥施用量变化率的乘积计算的固定弹性贡献率，模型2的贡献率是由公式5的弹性Ed2与化肥施用量变化率的乘积计算的变动弹性贡献率。从图4可以发现，利用模型1和2估计结果计算的化肥对单位面积粮食产量变化的贡献率均呈现出小幅波动，但总体呈现出下降趋势。

图4 单位面积粮食产量变化率及由模型估算的化肥贡献率Fig.4 Grain yield per unit area change rates and the estimated contribution rates of fertilizers

模型1的估计结果表明，化肥施用量的固定弹性系数大于其他要素，虽然根据模型2估计的化肥施用量的可变弹性系数出现了下降趋势，但在2015年仍然保持0.2的正弹性值，这意味着只要增加化肥的施用量还能带来一定程度的粮食产量的增加，化肥的增产效力不可替代。正是基于这一指标值的引导，当前化肥施用总量仍居高不下。然而从图4化肥对粮食产量变化贡献率可以看出，1995—2014年间的单位面积粮食产量变化波动频繁，且程度较大，甚至出现单位面积粮食产量减少的情况，虽然化肥对粮食产量的变动都呈现正向影响，但两个模型估计的化肥对粮食产量变动的贡献率均低于2%，并且2005年为最低值，仅为0.03% (模型1) 和0.05% (模型2)，虽然此后略有波动，总体而言，化肥对粮食产量变化的贡献率已渐趋近于0，这意味着化肥对粮食的增产潜力已基本被挖掘完。2015年单位面积化肥施用量已呈略微下降趋势，但粮食产量却实现1.81%的增加，这说明其他生产要素对粮食增产的贡献率在上升，而化肥对粮食产量增加的作用在下降。

3 结论与建议

本研究根据1995—2015年全国30个省份的面板数据估计了柯布道格拉斯和二项式函数形式的粮食生产函数模型，回归结果显示单位面积粮食产量对化肥施用量的弹性系数是正向显著的，且数值大于单位面积农机总动力等其他要素，证明了化肥是影响粮食单产的重要因素，对保障我国粮食产量稳定增长发挥了不可替代的作用。然而根据模型2估计的化肥可变弹性系数已经处于下降趋势，并且依据两个模型结果计算的化肥在粮食变化中的贡献率均逐渐趋近于零，这说明在目前中国粮食产量增加过程中化肥的作用已经很低，继续增加化肥施用量并不会带来产量大幅增加。2015年粮食投入产出数据分析结果也说明适当减少化肥施用量并不会导致粮食产量大幅减少，相反由于防灾技术、农业机械化程度的提高，其他要素对粮食产量的增加发挥了更大的作用。故建议一方面在从国家层面严格控制化肥施用量的继续增加，在稳定化肥投入总量的同时，通过调整施肥方式、优化施肥结构、对传统化肥增效改性等措施提高化肥的增产效率[22]；另一方面加强农业生产和防灾技术研发与推广、继续提高农业机械化程度，进一步发挥其他技术要素在提高化肥利用效率、促进粮食增产中的作用。