摆锤刀刃半径对冲击试验结果的影响
2018-08-16马辉刘志超朱锦波李学军
马辉 刘志超 朱锦波 李学军
天津出入境检验检疫局化矿金属材料检测中心天津300456
夏比冲击试验是金属力学试验中最基本的试验方法之一,冲击吸收能量是部分冶金产品质量标准对材料的检验指标之一,是评定金属材料在冲击载荷下韧性的重要手段[1]。其应用十分广泛,能够很好地反映材料的韧脆特性,对于各种内部缺陷和夹杂物引起的脆化非常敏感,但由于是在动态力下进行试验,所以影响夏比冲击试验结果正确性和分散性的因素很多,如试样的状态(尺寸、粗糙度、缺口类型及深度)、冲击试验机的状态(刚度、摆锤、轴线摆锤长度、刀刃尺寸、回零差、底座的跨距、曲率半径及斜度和能量损失等)、试验条件(冲击速度、试样对中、温度等)、试样材料的不均匀性以及操作人员的差异等[2]。其中摆锤刀刃半径为近年来争议较大的影响因素。
常用的摆锤刀刃半径为2 mm和8 mm两种,用符号的下标数字表示为KV2或KV8,摆锤刀刃半径的选择应参考相关产品标准。目前金属材料夏比冲击试验方法的国家标准GB/T 229-2007《金属材料夏比摆锤冲击试验方法》[3]和国际标准ISO 148-1:2009《金属材料夏比摆锤冲击试验第1部分:试验方法》[4]中指出:对于低能量的冲击试验,一些材料用2 mm和8 mm摆锤刀刃试验测定的结果有明显的不同,2 mm摆锤刀刃的结果可能高于8 mm摆锤刀刃的结果,但低能量冲击试验的适用范围并没有明确给出。针对摆锤刀刃对冲击试验的影响研究相关文献[5-7]指出KV8结果高于KV2,文献[8]认为KV2或KV8相差不大。因为这些结论大多数从试验结果分析得出,受到其他因素的影响,所以才会导致结论出现争议。
近年来围绕此类问题的研究大多仅局限于对某一种材料的试验结果进行对比分析,这些试验结果本身就是众多影响因素共同作用产生的,并不具备完整的代表性。如果只针对摆锤刀刃半径,而排除其他因素影响进行常规试验数据分析的难度较大。本文利用ANSYS有限元进行模拟分析,通过改变刀刃半径,对不同屈服点的材料,在相同条件下,对标准试样缺口的应力状态进行了动态模拟,分析了摆锤刀刃半径对冲击试验结果的影响。
1 试验材料与方法
试验选用屈服强度为150 MPa~1 100 MPa以内的各类可制作成冲击试样标准尺寸的样品,冲击试样长55 mm,横截面为10 mm×10 mm方形截面。冲击试验按照GB/T 229-2007[3]进行,缺口为V型,摆锤刀刃采用2 mm和8 mm两种,试验温度为0℃。
2 建立数值仿真模型
2.1 材料模型
采用合理的材料模型是数值模拟能够取得成功的必要条件,本次模拟试样选用了与应变率无关的双线性各向同性硬化模型,消除应变率对试验的影响,其本构关系方程为:

式中:ε为应变,σ为与应变相对应的应力,σy为材料屈服强度,E0为弹性模量,Et为切线模量。材料基本属性如表1。对于参与试验的冲头和砧座则采用刚性体模型,并且对模型的运动方向进行了限制,这样可以大大缩减显示分析的计算时间。
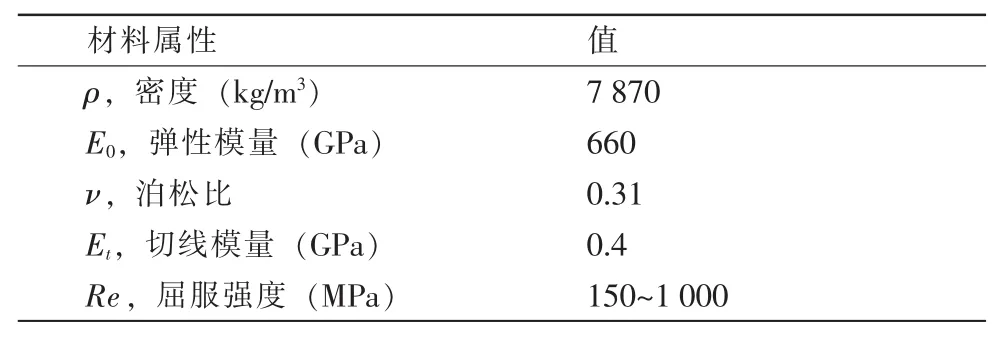
表1 材料基本属性
2.2 几何模型及网格的划分
根据GB/T 229-2007中对冲击试验的条件要求,试样在砧座上的跨距为40 mm,冲击试样长55 mm,横截面为10mm×10mm方形截面,试样长度中间有V型缺口,缺口有45°尖角,深度为2mm。因为此次计算结果只作为趋势性和对比性研究,为了减小计算量,将冲头模型简化,底部曲率半径忽略,但不影响冲击结果的对比。依据保证精度,提高计算效率的原则,以试件中心为对称建立的1/2几何模型,对试件采用较密的网格划分,其余部分采用相对粗的网格。
2.3 定义接触、约束和施加载荷
冲击过程是物体与物体间的表面接触,并且不需要发生穿透,所以采用ASSC自动接触。因为只有1/2的模型,所以在对称轴所在的平面定义了对称边界条件,并限制了X轴方向的位移。施加的载荷为时间-位移,如表2。为提高计算效率,时间均被缩小1 000倍,但不影响结果分析。
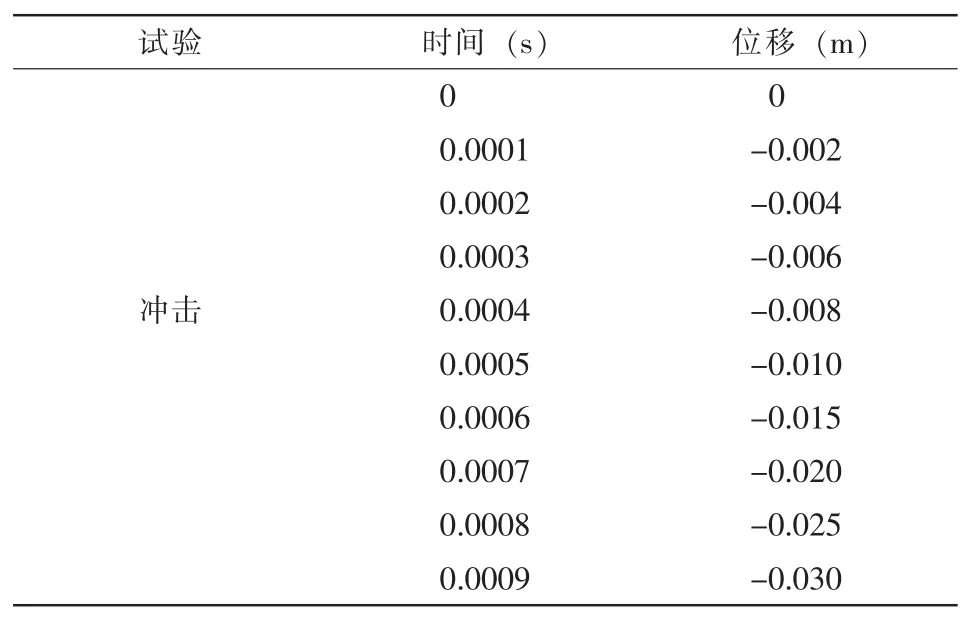
表2 施加的载荷
2.4 求解控制
在求解控制中,主要是设置质量阻尼与计算终止时间,其余的一些控制项可采用软件中的默认设置。计算终止时间应足够大到使模型中节点不发生振荡而形成稳定的残余应力场。可以预先设置一个时间值,然后以分析结果中模型能量时间曲线上动能为零的时刻作为最后的计算终止时间。
3 摆锤刀刃半径为8mm和2mm的冲击试验比较
3.1 摆锤刀刃半径为8 mm和2 mm的冲击试验模拟结果
图1为摆锤刀刃半径为8 mm和2 mm的冲击试验前后试样的应力云图,两种试样冲击后应力云图相似,应力主要集中在缺口及缺口周边区域,但8 mm的刀刃冲击后试样应力分布范围略大,主要是由于8 mm的刀刃作用区域面积更大。试样达到断裂前最大应力时的变形量基本相当,说明同一种材料,无论采用哪种摆锤刀刃,冲击试样都是弯曲到同一角度开始断裂。
3.2 摆锤刀刃为2mm的冲击试样单元最大等效应力-时间分析
试样材料模拟采用的屈服强度分别采用150~1 000 MPa,每增加50 MPa,进行一次模拟计算,并对单元H595,H604,H748,H757,H766,H775的等效应力最大值进行追踪分析,详见图2所标记单元位置。经过分析的计算结果见图3。各单元最大等效应力-时间曲线变化趋势基本一致,随着材料屈服点的提高,最大等效应力呈上升趋势,而达到最大等效应力所需要的时间呈现周期性波动变化。当屈服点达到750MPa以上时,波动变化幅度减小,呈现相对稳定趋势。
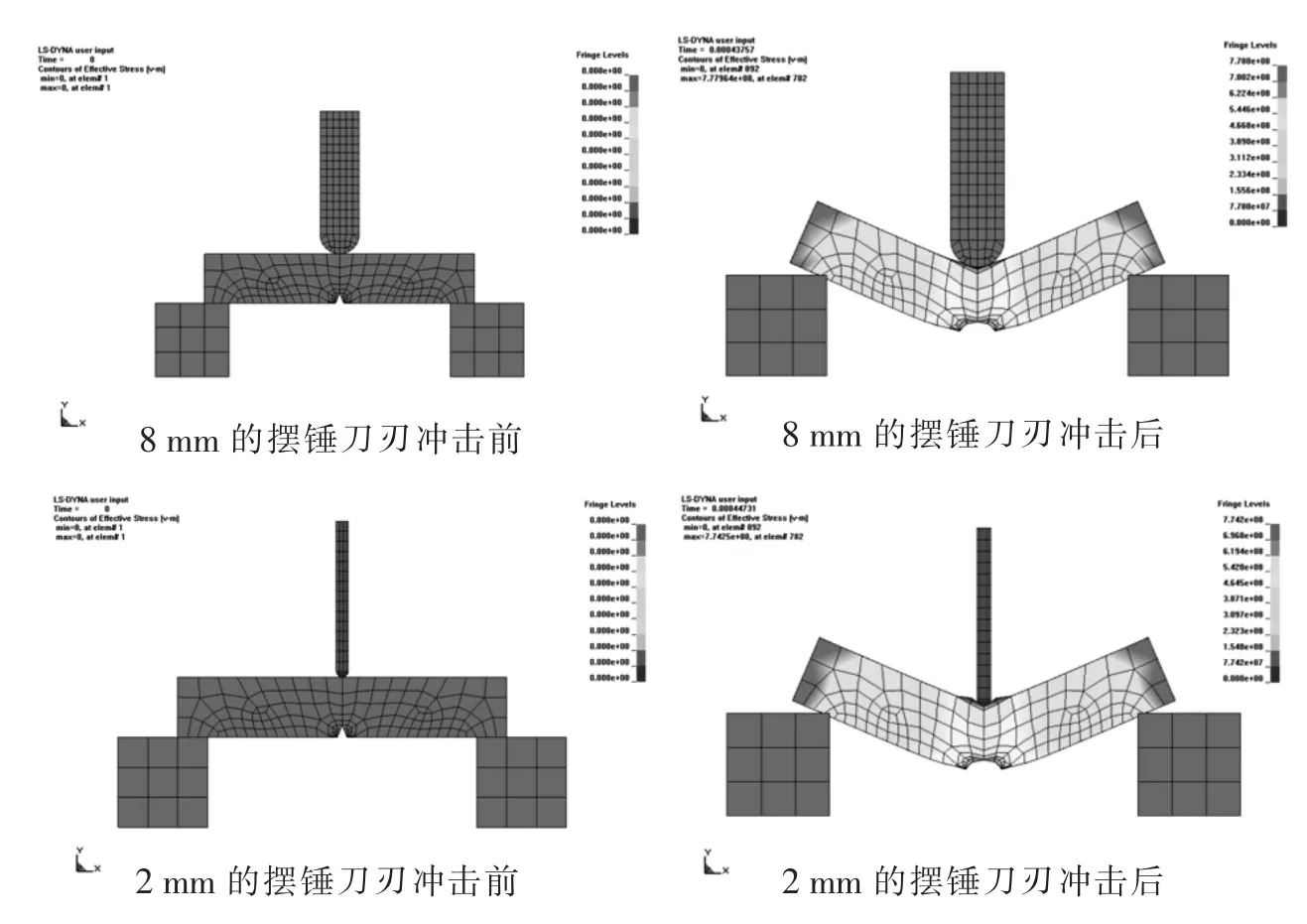
图1 摆锤刀刃半径为8 mm和2 mm的冲击试验前后应力云图
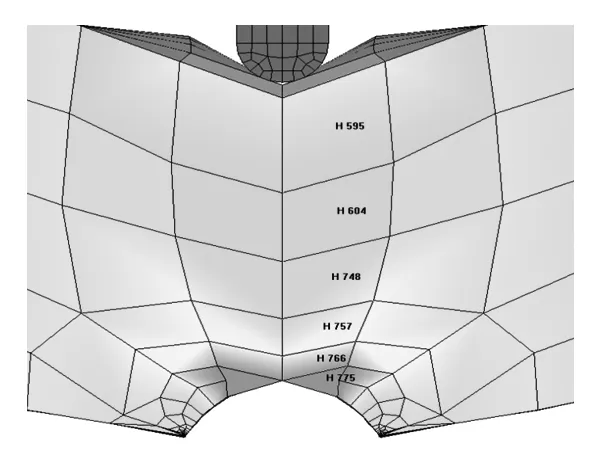
图2 单元H595,H604,H748,H757,H766,H775位置
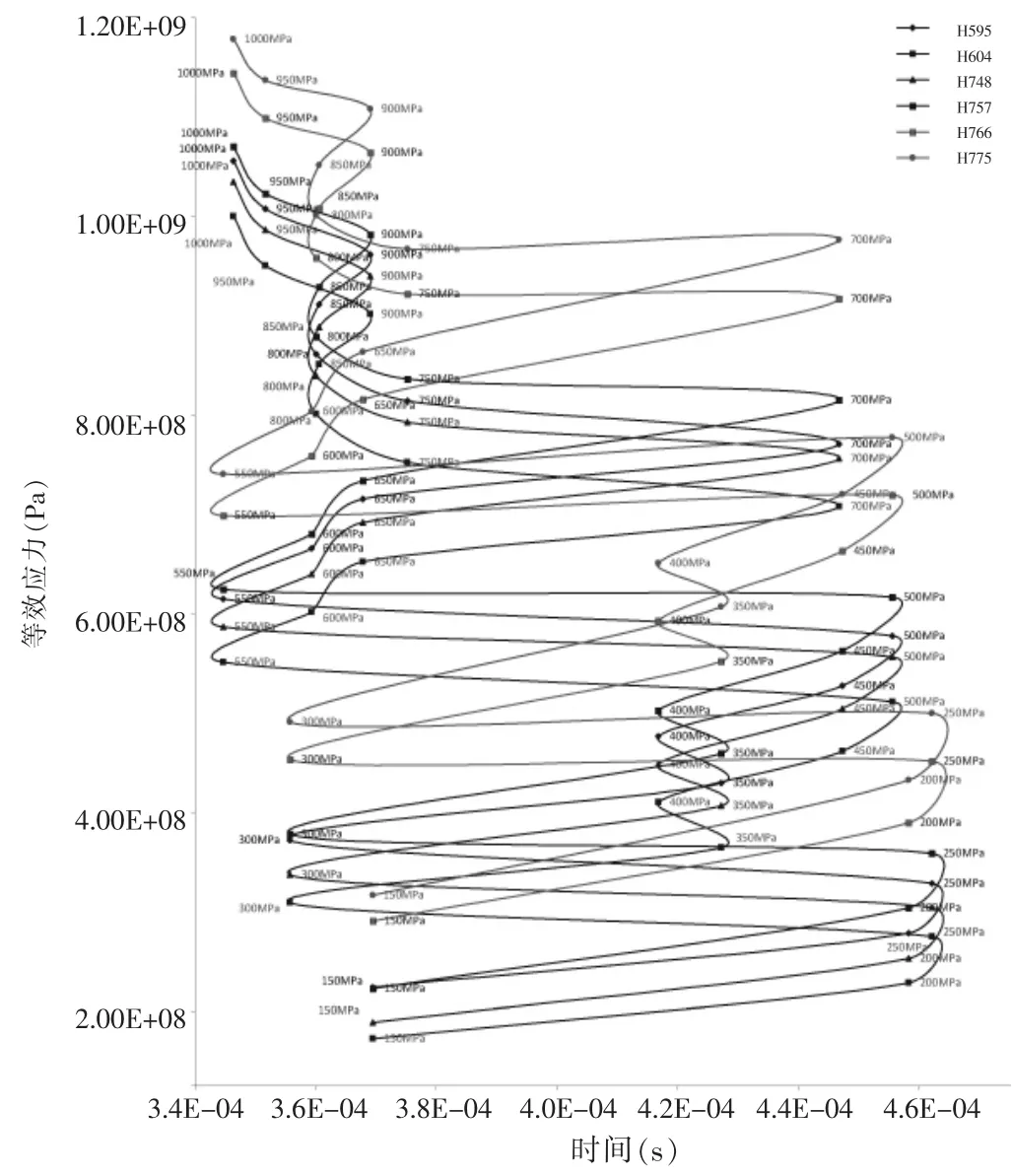
图3 摆锤刀刃为2 mm时,单元H595、H604、H748、H757、H766、H775最大等效应力-时间曲线
3.3 摆锤刀刃为8 mm的冲击试样单元最大等效应力-时间分析
图4 为摆锤刀刃为8 mm时,各单元最大等效应力-时间曲线变化趋势,与2 mm的刀刃冲击结果基本一致。随着材料屈服点的提高,最大等效应力呈上升趋势,而达到最大等效应力所需要的时间呈现周期性波动变化,但是变化的幅度更大。变化幅度减小并趋于稳定时,材料的屈服点为700 MPa。
3.4 对比分析摆锤刀刃为2 mm和8 mm的冲击试验模拟结果
单元H766和H775处于缺口尖端,根据Von Mises应力云图显示,在所有材料的完整冲击过程中H775和H766产生的应力最大。图5为摆锤刀刃为2 mm和8 mm时,单元H775和H766的最大等效应力-时间曲线。在同一刀刃半径下,两个单元的最大等效应力-时间曲线变化趋势相同,但是在不同刀刃半径下,变化有着明显的区别。经过对比分析发现,可以把整个变化过程分为3个部分。第一部分为屈服点处于1 000 MPa~750 MPa时,两种摆锤刀刃半径的模拟结果达到的最大等效应力及达到最大等效应力所需要的时间基本相当。第二部分为屈服点处于750 MPa~350 MPa时,两种摆锤刀刃半径的模拟结果达到的最大等效应力及达到最大等效应力所需要的时间交替领先。其中绝大部分为8 mm的刀刃半径冲击后达到的最大等效应力和所需时间大于摆锤刀刃半径为2 mm时的结果,只有处于750 MPa~700 MPa时,2 mm的刀刃半径达到最大等效应力所需要的时间大于8 mm时的结果。第三部分为屈服点处于350 MPa~150 MPa时,两种摆锤刀刃半径的模拟结果达到的最大等效应力及达到最大等效应力所需要的时间基本相当,其中处于300 MPa~200 MPa时,2 mm的刀刃半径达到最大等效应力大于8 mm时的结果。
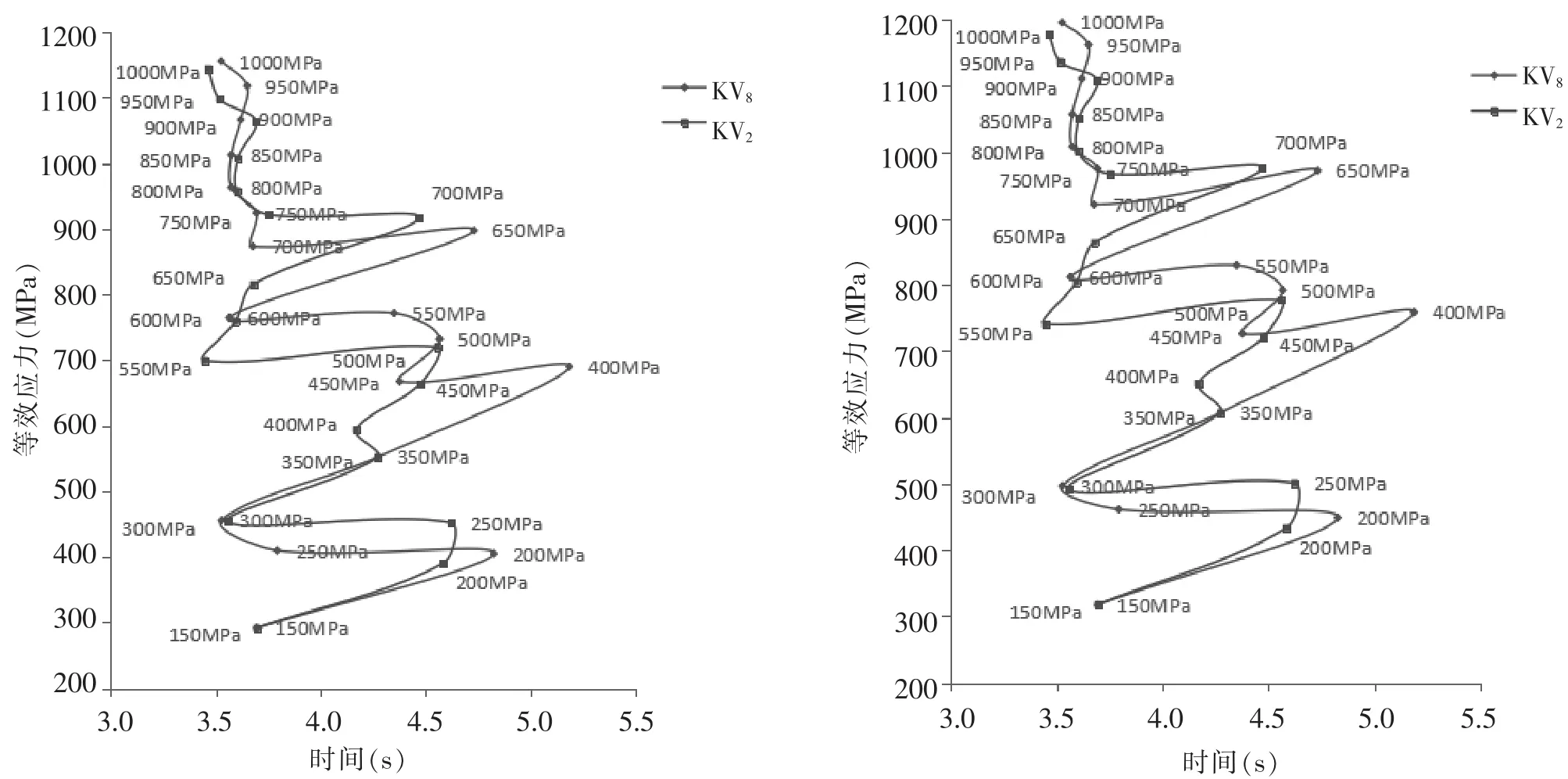
图5 单元H766和H775在摆锤刀刃分别为8 mm和2 mm时,最大等效应力-时间曲线
根据冲击试验原理,冲击吸收能KV=GH1-GH2,其中H1为冲击前摆锤高度,H2为冲击后摆锤上升高度。忽略空气等阻力,根据机械能守恒定律:GH=1/2mv2;动量定理:Ft=mv1-mv2,可得:

所以,冲击吸收能:

其中F、F′分别可以约等于KV2和KV8的最大等效应力;t、t′分别为KV2和KV8达到最大力所需要的时间;v2、v2′分别为KV2和KV8摆锤冲断试样后瞬间的最大速度;v1为摆锤接触试样前最大速度,由于初始势能相同,所以KV2和KV8摆锤接触到冲击试样前的最大速度相同;由于v1远大于v2、v2′,且v2、v2′相差不大,KV2、KV8的冲击吸收能可以简化为:
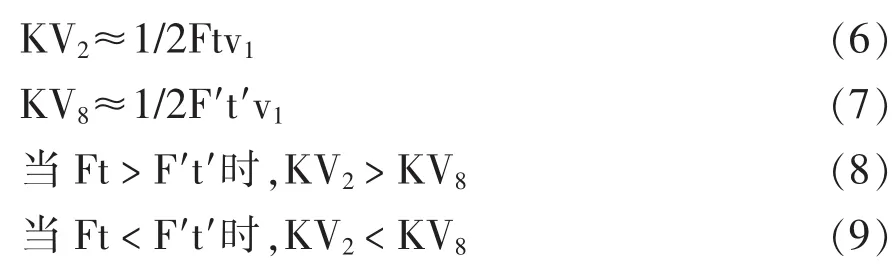
根据图5显示,并按照简化的冲击吸收能公式可以推出:当冲击试样材料屈服点处于1 000 MPa~750 MPa时,KV8和KV2基本相当,因为t、t′较小,此时冲击吸收能较小;当冲击试样材料屈服点处于750 MPa~700 MPa和300 MPa~200 MPa时,KV8小于KV2,当冲击试样材料屈服点处于700 MPa~350 MPa时,KV8大于KV2,这两部分冲击吸收能较大;当冲击试样材料屈服点处于350 MPa~300 MPa和200 MPa~150 MPa时,KV8和KV2基本相当,但因为F、F′较小,所以此时冲击吸收能也处于较低水平。
4 结果与讨论
参照模拟试验,在日常检验过程中选取屈服强度为150 MPa~1 100 MPa的材料,每次检测分别采用冲击刀刃为2 mm和8 mm的刀刃进行,检测仪器为Instron SI-1M型冲击试验机,执行的方法标准为GB/T 229-2007。因为检测结果为实测值,各类影响因素众多,但是通过增加试验次数,利用KV8与KV2之间的差值,分析差值与屈服强度之间的趋势关系,最大限度的排除其他影响因素,如图6所示。

图6 冲击吸收能KV8与KV2之间的差值与屈服强度之间的关系
经过分析发现,屈服强度为350 MPa~700 MPa之间的材料,绝大多数KV2的检测结果小于KV8;屈服强度为700 MPa~800 MPa之间的材料,绝大多数KV2的检测结果大于KV8;屈服强度为800 MPa~1 100 MPa之间的材料,虽然绝大多数KV2的检测结果小于KV8,但是之间的差值明显减小,且趋近于0,与模拟结果较为接近,证明整个模拟过程具有一定的合理性。
GB/T 229-2007中指出:对于低能量的冲击试验,一些材料用2 mm和8 mm摆锤刀刃试验测定的结果有明显的不同,2 mm摆锤刀刃的结果可能高于8 mm摆锤刀刃的结果[4],通过模拟结果表明这个低能量冲击试验的适用范围是当材料屈服强度为750 MPa~700 MPa和300 MPa~200 MPa左右时,KV2会大于KV8。但同时在这个低能量冲击试验的范围内,如果材料的屈服强度小于200 MPa或大于750 MPa时,那么KV2和KV8几乎相等。KV2和KV8产生的这些差别主要和材料冷脆的物理本质有关。冷脆断裂主要分为两种,一种为解理断裂,一种为微孔断裂;当温度在转变温度以上时,位错运动阻力低,即材料屈服强度低,这时在位错塞积群应力场作用下,解理断裂没有条件发生,塑性变形(位错运动)抢先产生微孔断裂;当温度低于转变温度时,位错运动阻力增加,即屈服强度增加,微孔断裂没有条件发生的情况下,解理断裂抢先产生[9]。上述过程中,不难发现冷脆的实质就是温度降低时,屈服强度提高造成的。也就是说温度影响的实质就是使材料屈服强度的升高或降低。如果将温度的降低,转化为屈服强度的升高来考虑,那么与图5显示的结论有着一定的规律性。结合部分典型冲击试样剪切断面率评定的结果见表3,可以推论认为:当冲击试样材料屈服点处于1000MPa~750MPa和350MPa~300MPa、200 MPa~150 MPa,冲击试样出现纯解理断裂形貌或者纯微孔断裂时,KV2和KV8都几乎相等。因为断口为纯解理断裂或者纯微孔断裂时,冲击刀刃的半径并不会影响冲击试样的断裂方式,此时冲击实验结果对冲击刀刃半径的影响并不敏感,所以KV2和KV8几乎相等。当材料屈服点处于750 MPa~700 MPa、300 MPa~200 MPa和700 MPa~350 MPa,冲击试样出现解理断裂和微孔断裂同时存在时,冲击刀刃的半径会影响两种断裂方式在断口所占的比例,所以此时KV2、KV8会出现一定的差异,部分典型混合断面形貌的差异见图7。

表3 部分典型冲击试样剪切断面率评定结果

图7 2 mm和8 mm摆锤刀刃冲击后,典型断面形貌之间的宏观差异
当前对于KV2和KV8的选择,各个国家和组织的标准都有各自的规定。其主要分为3个阵营,美国ASTM和API系列的产品标准基本上都规定采用方法标准ASTM A370中的试验方法进行试验。ASTM A370-2016《钢产品力学性能标准试验方法及定义》[10]对于冲击刀刃半径的选择规定只有KV8一种;欧盟EN系列的产品标准主要采用EN 10045-1:1990《金属材料-夏比冲击试验第1部分:试验方法》[11]和ISO 148-1:2009《金属材料夏比摆锤冲击试验第1部分:试验方法》[4]两种,EN 10045-1:1990中对于冲击刀刃半径的选择规定只有KV2一种,而ISO 148-1:2006规定却兼顾了美国ASTM和欧盟EN两个体系,有KV2和KV8两种;我国国家标准金属材料夏比冲击试验方法GB/T 229-2007为修改采用国际标准ISO 148-1:2006[3],其中对冲击刀刃半径的规定基本与国际标准一致。之所以出现这种格局,正是因为KV2和KV8的大小略有不同,不利于体系内数据横向对比和判定。我国当前同时采用2 mm和8 mm两种摆锤刀刃的冲击试验主要和我国当前发展水平和发展特点有关,但是未来随着我国技术水平的不断发展,对于此问题的影响应该在标准体系的发展过程中得到解决。
5 结束语
根据模拟结果推断,冲击吸收能KV8与KV2之间的差异主要取决于材料自身屈服点的高低,包括由于温度变化导致的屈服点变化。当断口为纯解理断裂或者纯微孔断裂时,KV2和KV8几乎相等,当断口为解理断裂和微孔断裂同时存在时,冲击吸收能KV8与KV2之间就会存在差异,差异的大小由所处的屈服点区间有关。
对于低能量冲击试验的适用范围是当材料屈服强度为750 MPa~700 MPa和300 MPa~200 MPa时,KV2会大于KV8。但同时在这个低能量冲击试验的范围内,如果材料的屈服强度小于200 MPa或大于750 MPa时,那么KV2和KV8几乎相等。当前冲击试验两种摆锤刀刃半径的选择应严格依据相关的产品标准要求,但在未来标准的制定和修订过程中,在材料KV2和KV8几乎相等的区间,应遵循互相替代的原则,进一步提高检测效率。
