借助几何直观发展逻辑推理能力的教学策略

陈文辉

几何直观是小学数学教学中快速提升学生逻辑推理能力的有力工具和方法。几何直观能够将概念、数字、运算、图形联系在一起，简化、明确内在数学逻辑关系。本文以几何直观为研究对象，分析了小学高年级数学教学中的痛点，并针对这些痛点，列举出具体的教学策略。

所谓“几何直观”，是指将概念、数学问题、关系等式转变为直观的图形，并在图形上找到解决问题的思路和方法。几何直观已经被列入十大核心概念，引导小学生探索数学知识，解决现实问题。步入高年级后，抽象问题具体化更需要借助几何直观来实现。数字、运算、图形以及几何关系都是数学学科解决现实问题的工具，它们之间没有界限，保持着内在逻辑的统一。因此，在高年级教学中，开展几何直观教学活动，从意识、方法和习惯上提升学生的逻辑推理能力，以便加深学生对数学知识的联系，多角度地思考问题。

一、小学高年级数学学习的几大痛点

高年级数学是一道隐性分水岭。从学生的角度看，学习存在以下几个痛点：第一，随着数学知识的增加，尤其引入抽象的数学知识后，学生便容易陷入迷茫期。虽然知识储备已经到位，却找不到合适的逻辑模型进行知识梳理、分类，做不出逻辑层面的数学知识框架。第二，对于涉及多个抽象概念、多个对象或者多个过程的问题，分析不清楚其中的逻辑关系，找不到对应的数学等式关系，难以攻克下有思维难度的题目。第三，对数学问题的转化意识、能力不够，缺乏正确绘图处理问题的能力。有的学生想到几何绘图解决问题，却不知道如何正确画图；有的学生根本想不到用几何直观来解决问题，使得学生对问题的考虑越来越糊涂。总之，高年级学生在数学的知识框架、逻辑关系和几何直观方法运用三方面存在着问题，需要通过开展对应的教学活动进行解决。

二、借助几何直观提升逻辑推理能力的教学策略

（一）运用几何直观，构建逻辑性知识框架

从知识框架角度看，几何直观能够剖析清楚不同逻辑板块之间的背后逻辑关系。对于小学高年级的学生而言，章节和模块知识框架的作用已经非常有限，而建立与几何直观相关的逻辑模型，构建逻辑性知识框架能发挥出极大的作用。借助知识框架，让学生从单纯的数学概念中脱离出来，侧重对数学知识内在逻辑性的理解和学习。

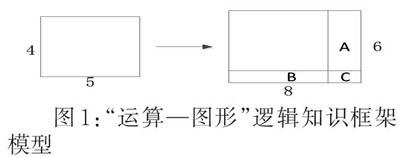
以“建立几何图形面积与运算之间的逻辑性知识框架”为例。比如：“4”对应着宽4长5的长方形面积。其内在逻辑是：抽象的运算规则和直观的几何面积有着对应关系。利用这种关系可以实现运算与几何图形关系的转化。在教学中，以这一基本关联为出发点，建立起基本的模型，并演示多个变形应用，便可以形成“运算—几何面积”逻辑知识框架。这一逻辑性知识框架的应用如下（图1）。不同题目会选择一些条件，既可以是如下所示提供边长变化，求面积，又可以是通过提供A或者B或者C的面积，求解边长。通过这一转化模型的讲解就能够构建起“运算—图形”的逻辑知识框架，解决图形变形产生的一系列问题。

（二）通过几何直观，明确问题的逻辑关系

对于脱离了规则图形长宽变化的逻辑性问题，还需要通过分析问题中的多个变量、前后状态，找到其中的逻辑关系，列出对应等式关系，从而解决复杂性问题。这些问题涉及相遇和追击问题、油桶重量问题以及选址问题等，将一元一次代数概念与应用、基本运算、逻辑推导分析联系在一起。通过几何直观的学习，学生能够克服大量的逻辑推导问题。

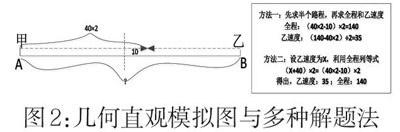
例如：以相遇问题为例，借助几何直观，明确逻辑关系。比如：甲从A地去B地，乙从B地去A地，二者同时出发，甲的速度为40Km/h，用了2小时，相遇时，甲的路程占全程的一半多10Km，求乙的速度和全程。在这一题目中，甲、乙二人同时运动，不借助几何直观图，学生难以将这些条件有效地组合到一起。为了明确问题中的逻辑关系，从两方面进行讲解：一方面绘制逻辑关系图；另一方面罗列多种解题方法，明确方法间的内在逻辑一致性，使学生清晰地认知代数方法和传统运算方法的本质。在教学中，可以借鉴以下方式（图2）。引导学生通过几何直观做出复杂运动过程的模拟效果。还要根据这一直观图分析传统计算方法和一元一次代数求解方法的异同，让学生能够脱离枯燥的知识概念，以具体的应用，去学习、体会。

（三）探索几何直观，找到正确的应用方法

几何直观并不是可以直接运用解答题目的方法。针对不同具体问题，几何直观有着不同的表现形式。在数形结合的思想下，研究出具体正确的应用方法，解决一类或者某一方面的问题是十分有必要的。为了能够找到更多的应用方法，教师需要从意识、探索和习惯方面入手，不断积累和更新应用方法，降低高年级数学学习阶段的难度。

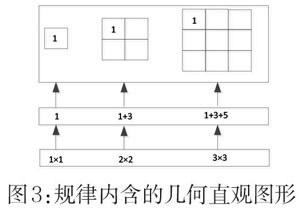
以找规律类型題目为例。首先，在弄清楚题目规律存在的条件后，将规律类题干提供的数字、图形、公式规律积累下来，从几何直观角度对规律进行还原。比如：“1，1+3，1+3+5，1+3+5+7……”向“1×1，2×2，3×3……”转化的几何直观图形（图3）。然后，对题干的规律进行深入扩展，一方面与所学知识进行联系，另一方面通过计算、验证分析，判断这些规律是不是可以扩展到更大的范围内容。比如：正方形面积公式向长方形面积推广；通过实际体积的验证，圆锥体积为圆柱的三分之一。最后，教师定期总结、归纳，为学生进一步将几何直观的具体例子系统化，并通过设计变形研究题目，指导学生选择性地应用几何直观方法。

三、结语

几何直观是小学数学教学的核心内容之一。通过抽象概念、复杂变化与几何直观内容的融合，将数学问题简单化，处理过程规范化，从而提高学生逻辑推理能力，达到多角度思考问题的教学目的。