物理学家为什么认为弦论是万有理论可能的候选者?
2018-08-15编译翟立建
编译 翟立建
弦论的核心思想是:宇宙最基本的组成单元不是0维的点粒子,而是一维的弦。弦论是物理学中未经证实的理论中最精妙、最具争议者之一。弦论的核心是贯穿物理学几个世纪的思想的主线,即在最基本层次上,各种力、粒子、相互作用和物理现象,都可由同一个理论描述,四种基本作用力(强力、电磁力、弱力和引力)统一于一个理论。
从许多方面来看,弦论是量子引力理论的最佳候选理论,量子引力理论恰好可以在最高能量尺度上将引力和量子物理统一起来。这一点,现在还没有实验证据,但在理论推理上有令人信服的理由。2015年,著名弦论学家爱德华·威滕(Edward Witte n)就写了一篇文章,提出每个物理学家应该了解弦论的内容。本文就是向非专业人士转述其意。

弦论的核心思想是:宇宙最基本的组成单元不是0维的点粒子,而是一维的弦
自然法则的非凡特点是:许多看似不相关的现象之间有诸多相似之处。它们背后的数学结构通常是类似的,有时甚至是完全一样的,比如,两个物体之间的万有引力与两个带电粒子之间的静电作用力在数学形式上几乎完全一样,钟摆摆动、弹簧上物体的往复运动和行星围绕恒星运行的方式完全类似,引力波、水波和光波都具有非常相似的特征,尽管它们的物理根源完全不同。同样,尽管大多数人都没有意识到,单个粒子的量子理论和量子引力理论也有类似之处。

标准量子场论描述的点粒子相互作用(左)与弦论描述的闭弦之间的相互作用(右)之间的差异

电子-电子散射费曼图,得到此图需要对粒子-粒子相互作用的所有可能进行求和
量子场论的工作原理是:你取一个粒子,然后对其可能进行数学求和。你不能仅仅计算:粒子过去的位置、现在的位置、如何到达所在的位置,因为自然界的基本粒子的固有属性——量子不确定性。正确处理方法是:把到达现在状态的所有可能路径(“过去的历史”部分)赋予正确的概率权重,再加起来求平均,然后就可以计算单个粒子的量子态。
如果你想研究的是引力而不是量子粒子,故事有所不同。因为爱因斯坦的广义相对论的处理对象不是粒子,而是时空的曲率,所以你不能对粒子所有可能的历史进行平均,而是对所有可能的时空几何进行平均。

引力由爱因斯坦广义相对论描述,其他三种基本作用力(强、弱、电磁相互作用)在根本上都由量子物理学所描述。相对论和量子论是两个独立的规则,共同掌管着宇宙的一切
三维空间几何问题是非常困难的。当一个物理问题具有挑战性时,我们通常会先尝试解决一个简单的版本。如果处理一维几何,问题会变得非常简单。一维曲面只有一种可能:弦。弦有开弦或闭弦之分,开弦具有两个独立、不相连的端点,而闭弦的两个端点连接在一起形成一个圈。三维空间中曲面的曲率复杂无比,而弦的空间曲率计算则简单许多。如果我们想用弦来描述物质,要处理的就是一组标量场(类似描述某些类型的粒子的广义坐标标量场)和宇宙常数(类似质量),这是非常美妙的类比。
只要你能定义出动量矢量,粒子在多维空间中获得的额外自由度就不会起到重要作用;动量矢量才是重要的维度。因此,在一维情形下,量子引力看起来如同具有任意维度的自由量子粒子。

含3价顶点的图是一维量子引力路径积分的关键组成
下一步将结合相互作用,从没有散射振幅或散射截面的自由粒子到产生物理效应、宇宙耦合的粒子。使用如左图可描述量子引力中作用的物理概念。如果我们把该图的所有可能组合都写下来并进行相加,应用如动量守恒定律的定律,我们就可以完成这个类比:一维量子引力非常类似任意维度的单个粒子的相互作用。
下一步是从一个空间维度扩展到3+1维度:三个空间维度加一个时间维度。但对于引力理论,这一“升级”可能非常具有挑战性。反其道而行之,可能会有更好的方法。
不去计算单个粒子在任意维度上的行为,不妨计算一根弦(不管开弦还是闭弦)的行为。然后,我们可以寻找类比,得到更完整的更接近现实维度的量子引力理论。

在任何特定位置发现量子粒子的概率都不会是100%;概率分布同时是空间和时间的函数
不从点和相互作用开始,而是直接从表面、膜之类的对象开始。真实的多维表面可以以非平凡的方式弯曲,呈现出很有趣的行为,这些行为可能是广义相对论所描述的宇宙时空曲率的起源。
虽然一维量子引力为我们提供了弯曲时空的粒子的量子场论,但它并没有描述引力本身。缺失了什么微妙的东西?算符(代表量子力学的力和性质的函数)与量子态(粒子及其性质随时间演变的方式)之间没有对应关系。这种“算符-量子态”对应是必要的,但却缺失了。
如果我们抛弃点状粒子,而采用弦状的实体,算符-量子态对应关系就会呈现出来。
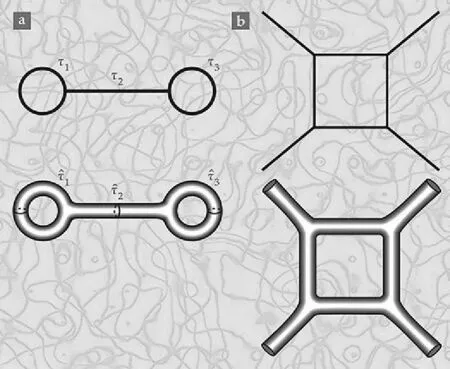
基于点粒子及其相互作用的费曼图(上图),通过类比,将之转换成弦论的费曼图(下图),线条成为具有非平凡曲率的表面
从粒子“升级”到弦,就存在真正的算符-量子态的对应关系。时空度量的涨落(即一个算符)自动表示描述弦性质的量子态。因此,我们可以从弦论得到时空的量子引力理论。
所得不止如此,还可以获得与时空中其他粒子和力相统一的量子引力,这些粒子和力对应于弦的场论的其他算符。仍然存在描述时空几何涨落的算符和弦的其他量子态。弦论的最大新闻是:它能提供了一个管用的量子引力理论。

时空度量可用涨落(图上标记为“p”)表示。如果将时空度量用于弦的类比,时空度量描述的是时空涨落,对应于弦的量子态

布莱恩·格林(Brian Greene)在做关于弦论的报告
然而,这并不意味着这是一个已知的结论,但是,弦论是通往量子引力的路径。弦论的最大希望在于:这些类比在所有尺度上都成立,弦的图像与我们观测的宇宙之间存在清晰、一对一的映射关系。
现在,弦或超弦的图像只在几种维度中自洽,而最有希望的一组并没有给出爱因斯坦所描述的四维引力。与之相反,我们发现了十维的布兰斯-迪克(Brans-Dicke)的引力理论。要获得我们四维宇宙的引力,必须“去除”6个多余的维度,并将布兰斯-迪克的耦合参数取为无穷。但是,如何从十维的布兰斯-迪克理论中得到爱因斯坦的引力和3+1维数仍然是弦论的一个待解决的挑战。

卡拉比-尤奥(Calabi-Yau)流形的二维投影,这是紧化弦论中多余的不想要的维度的常见方法
弦论提供了一条通向量子引力的路径,几乎没有其他的选项比得上弦论。如果我们做出明智的选择,找到“管用的数学”,我们就能从弦论中得到当前物理的两大高峰:广义相对论和标准模型,且弦论是到目前为止实现此目标的不二之选,因此,弦论成为热门的研究对象。无论你是热衷宣扬弦论的成功或失败,还是你对它缺乏可验证的预言有所想法,弦论无疑仍是理论物理研究中最活跃的领域之一。弦论核心思想是许多梦想完成终极理论的物理学家的最主要思想源。
资料来源 Forbes.com
