含缓倾软弱夹层的矿山高边坡长期稳定性分析

，，， ，

(中国地质大学(武汉) 工程学院，武汉 430074)

1 研究背景

在我国西南地区大范围存在含缓倾软弱夹层(岩层和夹层倾角<25°)的二叠系石灰岩地层[1-3]。该二叠系含缓倾软弱夹层的内摩擦角普遍接近或大于岩层倾角(缓倾地层)，并因此已引发了多起沿这类缓倾软弱夹层的大规模滑动破坏[4-6]。这些边坡滑动事故造成了严重的经济损失和大量的人员伤亡。由于这类缓倾软弱夹层的普遍存在，所以研究此类边坡对于各类工程边坡的稳定性评价、预测与控制有重要的实际意义。

对于岩质边坡稳定性的研究，一般采取定性分析、失稳模式判别和定量分析等方法[7-9]。软弱夹层的内摩擦角通常小于滑动面倾角，常规力学分析结果多显示边坡处于稳定状态，而这与现实中大量边坡变形破坏现象相矛盾。因此，目前国内外对含缓倾软弱夹层岩质滑坡的成灾机理颇具争议。Maranini等[10-14]通过岩石流变试验研究了沉积岩层中顺层平行剪切带的形成过程，认为顺层平行剪切带的形成是软岩蠕变、软弱层膨胀性、坡体重力作用下的差异性沉降、滑面带渐进式破坏以及河流侵蚀卸荷等因素作用的结果。刘晶辉等[15]认为软弱层是岩质边坡的稳定性的控制性因素，研究了软岩蠕变特性并对软岩长期强度的3种方法进行对比分析。

上述关于含缓倾软弱夹层边坡的稳定性分析的研究模型与方法中考虑多种岩层多种模型的情况较少。本文以四川省峨胜水泥采矿场变形体边坡为研究对象，采用常规力学试验与环剪流变试验得到各项参数，运用基于Burgers模型的计算方法对变形体边坡进行稳定性分析计算;综合现场监测数据，并与传统的极限平衡法、强度折减法进行对比，探讨此类边坡稳定性的影响因素。

2 研究区工程地质条件

四川省峨眉山市峨胜水泥采矿场变形体边坡位于峨胜采矿场后缘1 270～1 380 m平台，为采场终了边坡(如图1)。

图1 变形体边坡全景Fig.1 Panoramic view of deformed slope

该变形体边坡大部分岩体以灰绿色、青灰色厚层、中厚层状石灰岩为主，下部为深灰色厚层、中厚层状石灰岩，该组灰岩含有多层含泥软弱夹层(如图2)。这类软弱夹层岩性为原生灰色至灰黑色炭质泥页岩，手摸易染色，主要矿物成分为伊利石、方解石和石英，物理力学性质差。岩层倾向296°～325°，倾角14°～19°。潜在滑体厚度为10～58 m，滑坡体积380×104m3，可能形成大型岩质顺层滑坡。经矿山生产人员反映，该开采边坡出现局部变形迹象，边坡前缘1 270 m平台出现渗水现象，变形体位于高程1 380 m处出现规模较大的拉裂缝，整个变形体处于加速破坏阶段。

图2 炭质泥页岩软弱夹层Fig.2 Soft interlayers of carbonaceous shale

选取具有代表性的边坡剖面a-a′(如图3)作为研究对象，并进行岩石单轴、三轴压缩强度试验、岩石的直剪试验、结构面直剪试验。软弱夹层剪切试验成果如图4所示，常规物理力学参数如表1所示。

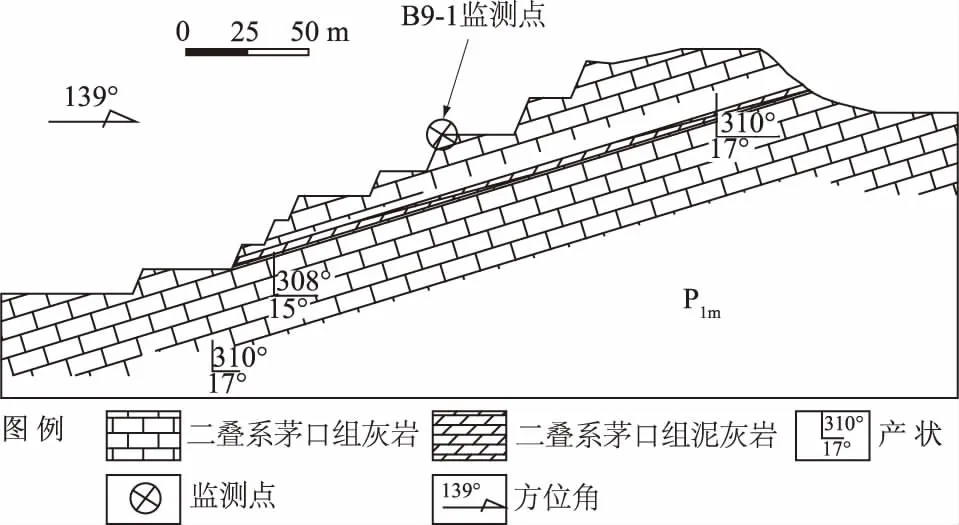
图3 峨胜水泥采矿场a-a′边坡工程地质剖面图Fig.3 Engineering geological profile of the slope of Esheng Mine

图4 软弱夹层大型剪切试验破坏后的试样Fig.4 Sample of soft interlayers after shear failure

岩性弹性模量/GPa密度/(kg·m-3)泊松比抗剪强度指标黏聚力/MPa内摩擦角/(°)石灰岩37.62 6600.3619.9353.62软弱夹层1.01 9500.3016.7024.25

3 基于环剪流变试验的Burgers流变模型计算方法

3.1 Burgers本构模型介绍

对含缓倾软弱夹层的边坡进行长期稳定性分析，需考虑时间因素对软弱夹层的影响，选取最适合软岩的Burgers模型对软弱夹层进行分析。Burgers模型是由马克斯威尔体与开尔文体串联而成，其力学模型如图5所示。

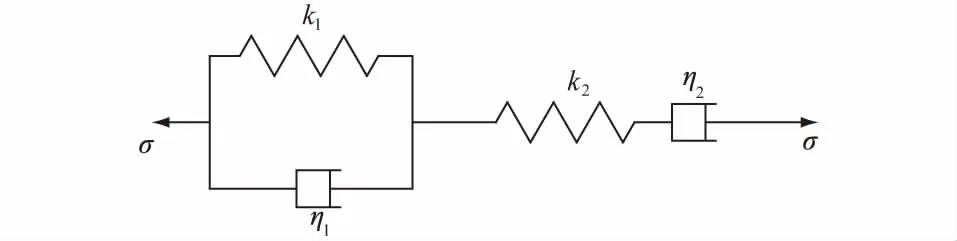
图5 Burgers体力学模型Fig.5 Mechanics model of Burgers body

Burgers体的本构方程为

(1)

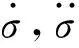
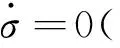
(2)

3.2 环剪流变试验

环剪试验是一种空心扭剪试验，由于试样宽度相对于土环半径而言较窄，可以克服实心扭剪试验中剪切面上正应力和剪应力分布不均的现象，因而可假设剪应力沿剪切面是均匀分布的[16]。

环剪试验过程中监测得到的数据主要为剪应变和平均剪切位移(本文简称剪切位移)，剪应变γ的计算公式为

(3)

式中：r1，r2分别为环形试样的内径、外径；h为试样的高度；θ为转过的角位移。剪切位移S满足如下关系：

S=2πavt；

(4)

(5)

式中：a为试样的平均半径；v为环剪速率；t为剪切时间。

采用ARS型环剪仪对茅口组软弱夹层进行环剪流变试验，试样为原状样，采取法向压力为400 kPa、切向压力分6级加载(如表2)，记录6级荷载轴压下的应变-时间曲线，对其进行研究。试验过程中显示第6级加载时已经破坏，因此本文研究前5级荷载下的应变-时间曲线。

表2环剪流变试验分级荷载

Table2Steppedloadingofcyclicsheartest

法向压力/kPa切向压力/kPa第1级第2级第3级第4级第5级第6级40024.148.272.396.4120.5129.8

将试验得到的应变-时间数据利用Origin软件采用Burgers模型进行拟合，得到如图6所示的拟合曲线，进行比对分析选取最优参数，如表3。

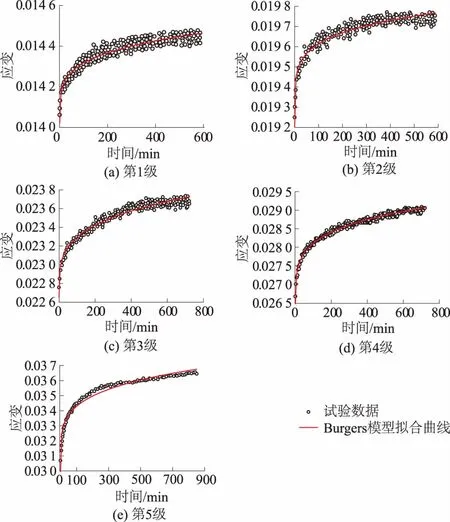
图6 环剪流变试验分级加载结果及Burgers模型拟合曲线Fig.6 Fitted curves of strain-time relation in cyclic shear rheology test by Burgers model

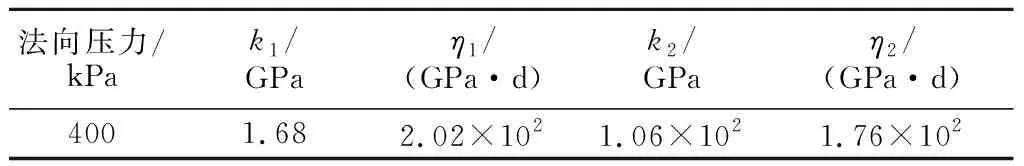
法向压力/kPak1/GPaη1/(GPa·d)k2/GPaη2/(GPa·d)4001.682.02×1021.06×1021.76×102

4 实例应用数值模拟计算分析

4.1 网格模型的建立

利用FLAC3D软件对变形体边坡进行计算分析，FLAC3D采用显式有限差分来模拟三维连续介质的力学行为，进而模拟含缓倾软弱夹层的边坡稳定性是可取的。选取具有代表性的剖面a-a′(如图3)，采用ANSYS软件进行建模与网格剖分，其中软弱夹层部分网格进行加密，将边坡模型导入FLAC3D中，得到网格模型如图7所示(共剖分3 260个网格与6 768个节点)，利用FLAC3D对底面、左右两侧以及y轴方向进行全约束。考虑到石灰岩具有较强的力学性质，上下2层灰岩采用表1的参数，本构模型采用摩尔-库伦模型，中间软弱夹层采用表3 的参数，本构模型采用Burgers模型进行数值计算，模拟计算时间为365 d。

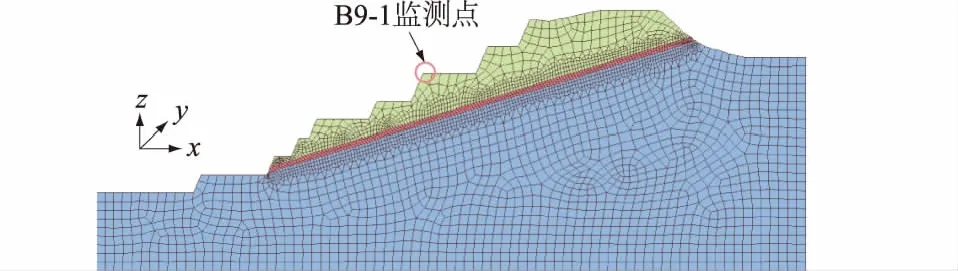
图7 网格模型Fig.7 Mesh model

4.2 数值计算结果分析

基于Burgers模型的计算结果如图8所示。

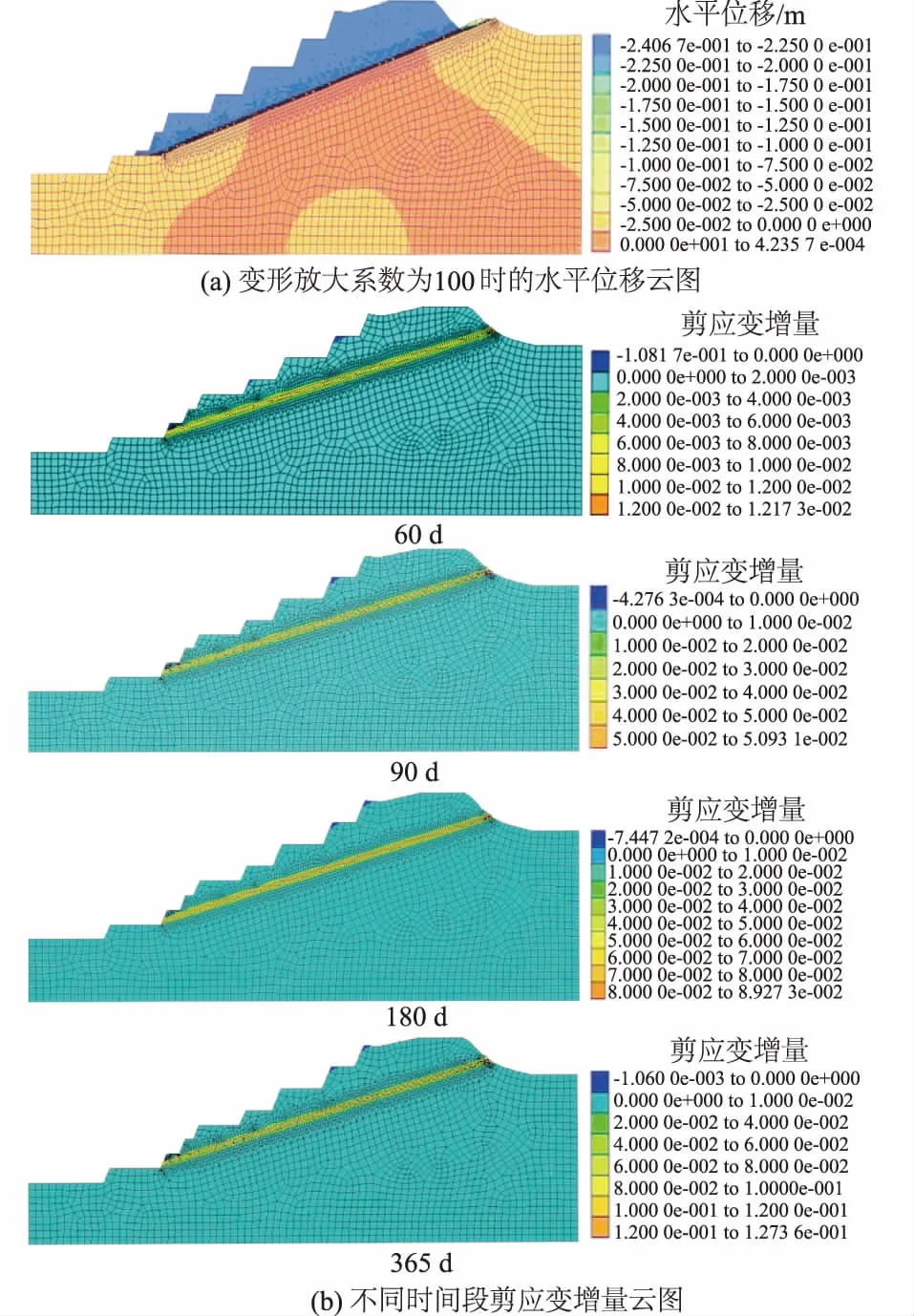
图8 基于Burgers模型的计算结果Fig.8 Calculation results based on the Burgers model

分析图8(a)可知，基于Burgers流变模型的计算方法在1 a模拟时间内最大水平位移达到了24 cm，在变形放大系数放大到100时能很明显看到上覆灰岩沿着软弱夹层产生下滑破坏。

由图8(b)可知，该边坡的软弱夹层剪应变贯通整个软弱夹层，可认定软弱夹层为滑动破坏面。由4幅不同时间段的剪应变增量云图还可看到，在剪出口位置剪应变随着时间的增加而增加，且模拟12个月后剪应变增量的数值几乎为强度折减法结果的4倍。从长期稳定性的角度考虑，边坡处于较危险状态，极易产生破坏。

选取具有代表性的监测点实测数据与模拟结果进行对比(图9)。由图9可知，该模型监测点的位移与实测位移的拟合度较高，表明此模型能够较好地反映该边坡的实际情况。

图9 实际位移监测数据与数值模拟结果对比Fig.9 Comparison of displacement between monitoring and numerical simulation

图10 极限平衡法计算结果Fig.10 Calculation result by limit equilibrium method

4.3 传统计算方法对比

为了得到最不利情况下边坡的稳定性状况，分别利用极限平衡软件Slide和FLAC3D强度折减法对边坡进行了稳定性计算，采用岩土体残余强度参数得到稳定性系数分别为1.58和1.59。极限平衡法计算结果和基于摩尔-库伦模型的强度折减法计算云图分别如图10和图11所示。强度折减法计算结果显示该边坡最大水平位移4 cm左右，且边坡整体剪应变增量偏小，未贯通，反映该边坡足够稳定。

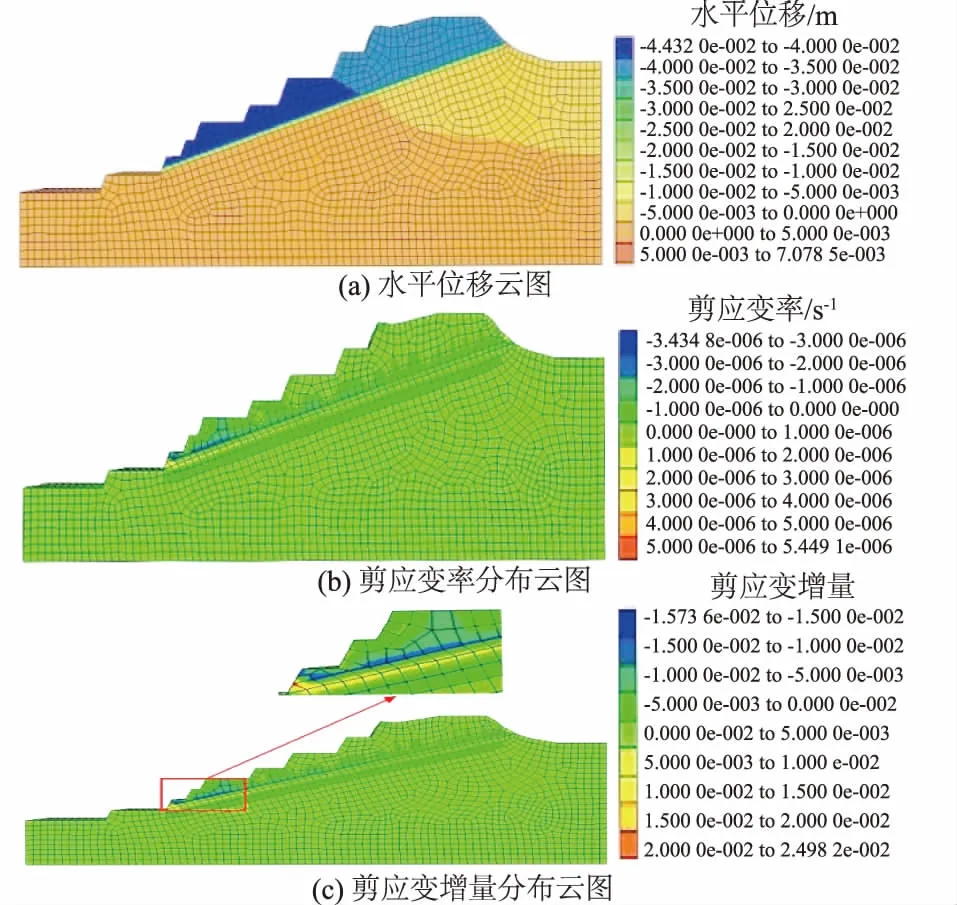
图11 基于摩尔-库伦模型的强度折减法计算云图Fig.11 Calculation result by strength reduction method based on Mohr-Coulomb model

综合2种传统方法对含缓倾软弱夹层的边坡稳定性系数的计算结果，极限平衡法与基于摩尔-库伦模型的强度折减法均不能科学合理地表现出该边坡的长期稳定性，而基于Burgers流变模型的计算方法与实际相符合，且具有代表性的模拟监测点位移曲线与实际监测位移曲线拟合度较高。考虑到灰岩较强的强度特性，本构模型选取摩尔-库伦模型,而对于可能导致边坡破坏的软弱夹层采用Burgers模型进行数值计算是合理的。

5 结 论

本文依托四川省峨眉山市峨胜石灰石矿山变形体边坡优化工程项目，对含缓倾软弱夹层的石灰岩矿山变形体边坡的长期稳定性进行研究，得到主要结论如下：

(1) 此矿区大面积覆盖二叠系石灰岩矿，石灰岩中夹有多层灰色至灰褐色炭质泥页岩软弱夹层，物理力学性质差、流变特性明显，其流变力学行为可用Burgers模型来描述。

(2) 选取常规力学试验和环剪流变试验的数据，利用Burgers模型进行反演，数值模拟计算得到的结果符合实际情况(整个边坡已经呈现破坏趋势)。极限平衡法和FLAC3D强度折减法2种传统方法的计算结果均显示该边坡稳定，但体现不出长时间下的潜在破坏;基于Burgers模型的计算方法中的模拟监测点位移与实际监测点位移拟合度高，表示其流变特性在边坡变形机制中是主要影响因素。

(3)对于此类含缓倾软弱夹层的边坡长期稳定性分析，在有足够的工程地质资料时，可以根据不同岩层建立不同的模型进行计算分析，软弱夹层可利用基于Burgers流变模型的方法进行数值模拟计算。