考虑组分活度的多组分污染物扩散模型

，

(北京工业大学 城市与工程安全减灾教育部重点实验室，北京 100124)

1 研究背景

在废弃物处置的环境工程中，多用压实黏土衬垫系统或黏土类防渗屏障。由于压实黏土垫层的渗透性极低，在污染物从垃圾填埋场垫层通过隔离屏障向周围地下水运移的过程中，分子扩散是污染物主要的运移形式。因此研究污染物在黏土防渗垫层中的扩散规律对预测填埋场的防渗系统的安全性具有重要意义。

Du等[1]、席永慧等[2]开展室内扩散试验，发现混合盐溶液中离子扩散系数较在单一盐溶液中的离子的扩散系数小。陈云敏等[3]、谢海建等[4-5]建立了层状土中污染物的一维扩散模型，得到其解析解，考虑有机污染物浓度随时间的变化，对污染物在复合衬层中的一维扩散问题进行了解析求解。张文杰等[6]分析了常用的零浓度边界、零浓度梯度边界和半无限边界对应的试验条件，求得各边界条件下统一的有限厚度土层中对流—扩散—吸附解析解。Quintard等[7]研究了多孔介质中非线性多组分质量传递问题，考虑组分的动量平衡方程，通过体积平均方法把微观上不连续的质量传递方程扩展到宏观上连续的质量传递方程；武文华等[8]介绍了多孔多相介质中溶混污染物的迁移，主要考虑对流、扩散及降解、吸附等机制，并对质量传递过程进行了数值模拟。Class等[9]在多孔介质中多相、多组分非等温条件下流动和迁移过程中考虑了相间的质量和能量的传递，提出了更合理有效的数值模拟方法，能够有效求解强耦合的偏微分方程。一方面，现有的模型多采用传统的Fick定律，仅能描述单组分污染物扩散现象，不能反映污染物多种离子(组分)间的相互作用；另一方面，在污染物迁移过程中，因多元化污染物共存而导致的组分间相互作用，使得每种污染物参与运动的浓度并不能发挥出其输入浓度数值大小的作用，导致现有模型均未能考虑多组分污染物溶液的非理想性，即组分活度的影响。

本文基于混合物组分线性动量平衡，引入活度系数以表示各组分污染物实际发挥作用的浓度与理想溶液中浓度的偏差，建立考虑组分有效浓度的一维多组分污染物扩散模型，以期为固废堆场防渗层有效厚度的设计以及服役性能的评估提供理论指导。

2 模型建立

2.1 基本假定

建立多组分污染物在黏土衬垫中的扩散模型时，主要假设包括：①土体是饱和、均质连续体；②污染物运移只发生在竖直方向；③污染物在土体中的运移机制仅考虑分子扩散作用；④污染物仅为电解质溶液。

2.2 组分活度系数

填埋场渗滤液中，污染物中组分的活度系数是溶液热力学性质的重要指标，能够反映溶剂(水)中离子之间及离子与溶剂(水)分子之间的相互作用，这种作用使得污染物组分的总浓度不能代表其有效浓度。则需引入一个经验校正系数(活度系数)，以表示实际溶液与理想溶液的偏差[10]。活度系数是指组分活度与浓度的比例系数，能够表征组分实际参与运动的有效浓度。

电解质溶液理论是众多涉及研究溶液化学性质领域的基础理论，在环境土工方向如在研究填埋场渗滤液在黏土隔离衬垫中的扩散规律时也同样适用。其中电解质的活度系数是研究渗滤液热力学性质的基础。本文采用Davies提出的活度系数经验方程,即

(1)

2.3 多组分污染物扩散方程

在空间位置Χ和t时刻，若多孔介质液相中多组分污染物由m个组分构成，则多组分混合物中i组分引入了组分活度系数的动量平衡方程,可写为

(2)

式中：ρi是i组分的质量密度；Di/Dt表示对i组分的全导数符号;vi是i组分的运动速度；T,pμi为i组分在等温等压时的化学势梯度，T为温度，p为压强,μi为i组分的化学势；是i组分的摩尔体积；τi为i组分的部分偏应力张量；gi是作用在单位质量i组分上的外部体力；vj是溶液中其他组分j的运动速度；ζij是i组分与其它组分j的摩擦系数；ζis是i组分与多孔介质骨架间的摩擦系数。

式(2)左边:第1项为i组分的扩散加速度项；第2项，第3项与第4项之和为作用在i组分上的表面力作用项；第5项为i组分的外部体力作用项(如重力、离心力、电场力、电磁力等)。右边:第1项为由于浓度梯度而产生不同组分间相对速度造成的组分间内部摩擦力；最后一项为i组分与多孔介质骨架摩擦的作用力。

式(2)即为液相多组分污染物中i组分扩散满足的动量平衡方程式。

Krishna[11]给出组分i化学势的本构关系为

μi=μ0(p,T)+RTln(rixi) 。

(3)

式中：μ0为理想溶液的标准态化学势；R为气体常数；xi为组分i的质量分数，定义为

xi=ρi/ρ。

(4)

其中ρ为孔隙液相平衡溶液中所有组分质量密度之和。

则可得等温等压条件下的化学势梯度为

T,pμi=RTln(rixi) 。

(5)

(6)

式(6)即多组分污染物扩散方程，该方程能够考虑多组分污染物扩散过程中由浓度梯度造成的组分间摩擦作用和组分与多孔介质骨架的摩擦作用，以及组分有效浓度的活度系数的影响。方程左边为溶质扩散的驱动力(包括化学势梯度、压强梯度、组分分子表面的剪应力、各种外部体力、以及扩散加速度产生的力)；方程右边为浓度梯度作用下组分i所受内部作用力(包括组分间摩擦力和组分与多孔介质骨架间的摩擦力)。

3 模型验证

为验证所建扩散方程的合理性及正确性，将本文所建扩散模型与文献[12]中一组试验数据作对比，试验用自制的三区域容器测定了63 d内CaCl2与KCl复合溶液中钾离子浓度与钙离子浓度在黏土中扩散距离的变化关系，所采用的2种组分活度系数参考文献[13]，Ca2+,K+的活度系数分别为0.65,0.62，对比结果如图1所示。

图1 土体试样中离子浓度随扩散距离变化曲线Fig.1 Relationship between ions concentration and diffusion depth in clayey soil

由图1本文模型模拟结果和席永慧等[12]试验结果对比可见本文模型模拟结果与席的扩散试验结果整体趋势较为一致。

4 数值求解与分析

4.1 定解条件

为求得模型的数值解，作出假设包括：①堆场底部由天然黏土层和不透水层构成，如图2所示；②土层上表面排水；③不考虑土体中污染物的背景浓度。

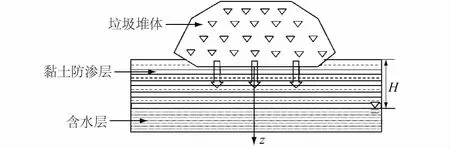
图2 污染物在黏土层中的运移示意图Fig.2 Schematic diagram of one-dimensional transport of contaminants in clay liner

本文多组分污染物扩散模型的定解条件如下。

初始条件：

ρi(z,0)=0 , 0≤z≤H。

(7)

边界条件：

ρi(0,t)=ρi0,t≥0 ；

(8)

(9)

式中：z为运移深度；H为防渗层厚度；ρi0为i组分污染物边界质量浓度。

4.2 参数选取

本文主要研究对象为垃圾堆场渗滤液，为了保证数值模拟具有代表性，在本文模拟多组分污染物扩散时，选取渗滤液溶质种类中具有代表性的铜(Cu2+)、镍(Ni2+)2种重金属污染物。输入浓度设为恒定源，模拟其混合物在饱和土体中的扩散规律。

为考虑组分活度系数的存在对多组分污染物在黏土垫层中扩散规律的影响，选取铜(Cu2+)、镍(Ni2+)2种不同的活度系数研究离子在黏土垫层中的扩散规律。模型参数选取如表1。

本文取2组活度系数，分别为理想溶液中2种污染物活度系数均为1以及Cu2+和Ni2+活度系数分别为0.309，0.355[10]2种工况，见表2。

利用有限元软件COMSOL Multiphysics对模型进行数值模拟求解，得到黏土层中污染物浓度随时空扩散的分布规律。

4.3 数值结果及分析

为便于求解，考虑多组分污染物在等温等压的情况下扩散，忽略惯性力项、部分分子偏应力项，以及外部体力项。

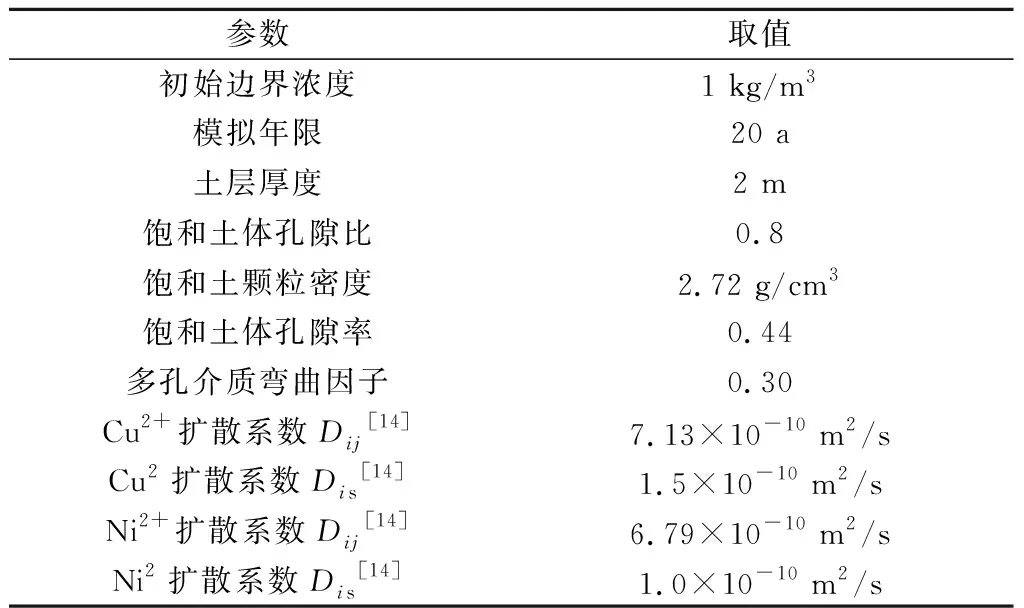
表1 模型参数Table 1 Model parameters

表2 两组分污染物的活度系数Table 2 Coefficient of activity of two components in the transport model

而在传统堆场设计时，多用Fick定律来描述扩散数值模拟结果。本文数值模拟3种工况，分别为基于Fick定律单组分扩散、考虑污染物分别为理想溶液和非理想溶液的两组分扩散。3种工况的组分初始边界浓度均为1 kg/m3。

图3 特定年限Cu2+浓度随深度变化曲线Fig.3 Variation of Cu2+concentration against depth at different years

图4 特定年限Ni2+浓度随深度变化曲线Fig.4 Variation of Ni2+ concentration against depth at different years

数值模拟结果如图3和图4所示。由图3与图4可知，不同工况下的污染物浓度随土层深度的变化规律总体趋势相似。同一运移年限时，各土层深度处，考虑真实活度系数时的两组分Cu2+(Ni2+)浓度小于理想溶液活度系数为1时对应的两组分Cu2+(Ni2+)浓度，且两者均小于只考虑基于Fick定律单组分扩散时的Cu2+(Ni2+)浓度。随着运移年限的增加，考虑真实活度系数时的Cu2+(Ni2+)的运移滞后于理想溶液中两组分Cu2+(Ni2+)的运移的程度越来越大，且两者均滞后于基于Fick定律单组分污染物的运移进程。传统堆场设计中，多用Fick定律来描述污染物在填埋场黏土衬垫中的扩散[3-5]，而由本文的图3和图4模拟结果可知，多种污染物在土体中扩散应当考虑溶液的非理想性即各自组分的活度。

对污染物扩散进程的快慢影响不仅包括污染物在孔隙液相中的扩散系数，还应当考虑多组分污染物共存时各自的活度系数。

防渗垫层有效设计厚度的选择，对周围土水以及废物堆场的风险性评估均具有非常重要的意义。根据《地下水质量标准》的有关规定，生活饮用水须符合第三类标准。分别取Cu2+浓度>1.0 mg/L，Ni2+浓度>0.05 mg/L的地下水视为被污染，因此本文取孔隙水中溶质离子浓度超过其限值范围对应的土层深度即为溶质的运移距离。Cu2+和Ni2+在防渗垫层中运移深度如图5所示。

图5 不同年限组分Ni2+和Cu2+的运移深度Fig.5 Transport depth of Ni2+ and Cu2+ against time

对比图5(a)及图5(b)模拟结果可知，选取不同的扩散模型和不同的组分活度系数所得数值结果并不相同，污染物运移深度均随运移年限的增加而增大。随着运移时间的增加，在扩散过程中考虑组分的真实活度系数时的两组分Cu2+(Ni2+)运移到某一深度所需时间大于考虑理想溶液中两组分运移到相同深度所需时间，并且2种工况所需运移时间均大于基于Fick定律的单组分运移到相同深度所需时间。同一运移时间内，考虑真实活度系数时的两组分Cu2+(Ni2+)的运移深度明显小于理想溶液活度系数为1时对应的两组分Cu2+(Ni2+)运移深度。由此可见，是否考虑组分的活度系数能够影响组分在多孔介质中的扩散行为，对扩散时间和扩散深度均具有非常重要的影响。因此，针对实际工程中的堆场防渗垫层设计而言，在多组分污染物并存的现场工况下，宜选用本文所建考虑有组分活度系数的多组分污染物扩散模型，在保证安全性的前提下，能够进一步提高堆场隔污防渗屏障有效厚度设计的合理性和经济性。

5 结 语

本文基于多组分混合物的组分线性动量平衡，引入可考虑组分有效浓度的活度系数，建立了多孔介质中多组分污染物在黏土垫层中的一维扩散模型。采用有限元软件COMSOL Multiphysics对扩散模型进行数值模拟求解，研究了组分的活度对污染物浓度随时空分布规律的影响。

(1)将多孔介质中多组分污染物扩散过程与传统的Fick定律描述的单组分扩散过程对比可见，在描述堆场渗滤液向隔离衬垫扩散的实际工程中，应当采用多组分污染物扩散模型。

(2)多组分污染物扩散过程中，应当在扩散模型中考虑多组分污染物共存时各自的活度系数。本文所建立的考虑组分有效浓度的一维多组分污染物扩散模型为实际环境岩土工程中设置合理、经济的防污屏障提供理论依据。