基于互信息与神经网络的天山西部山区融雪径流中长期水文预报

，， ， ，，

(新疆农业大学 水利与土木工程学院，乌鲁木齐 830052)

1 研究背景

准确的径流预报不仅有助于合理配置水资源，更好地支撑所在区域的工农业生产，而且可以帮助减少气象灾害带来的损失。目前，许多预报模型和组合模型都已应用在中长期径流预报中，如人工神经网络模型[1]、灰色-周期外延模型[2]、组合小波神经网络模型[3]等。人们对各种预报方法及模型进行研究发现，模型的输入变量在一定程度上影响着水文预报的精度[4]。不同研究区其流域径流量受不同相关因子的影响程度也大不相同，因此对研究区相关预报因子的选择成为影响该研究区径流预报水平的关键因素。目前，已有学者对如何选择径流预报因子的问题进行研究:朱永英等[5]借助粗集理论对预报因子进行优化和选择，提高了大伙房水库的中长期径流预报精度;闪丽洁等[6]运用不同方法优选长江流域预报因子建立人工神经网络模型进行径流预报，对比得到精度最高的预报因子挑选方法。然而，目前基于互信息理论进行预报因子选择的研究较少。赵铜铁钢等[7]运用了互信息法确定预报因子对长江各水文站建立神经网络径流预报模型；卢迪等[8]采用互信息量方法筛选预报因子作为BP神经网络的输入数据，对碧流河流的汛期径流进行中长期预报。研究表明互信息量方法可以识别出预报因子与径流的复合相关性，运用互信息挑选出的预报因子作为模型输入可以大大提高模型的预测精度。

新疆天山西部山区河流的补给以融雪为主，区域的水资源相对匮乏，准确地预知该区域的径流量尤其重要，既能够支持当地工农业生产，又对当地社会安定和合理安排水资源起着决定性作用[9]。鉴于不同区域产汇流规律、地貌特征及人类活动等的差异性，目前已有模型并不具有通用性。因此开展天山西部山区水文中长期预报的研究具有重要的意义。本文针对天山西部山区融雪径流预报中气象预报因子的选择问题，基于互信息理论对神经网络预报模型的输入因子选择及衡量因子间复合相关关系的方法进行研究与讨论。首先，通过不同的方法初步选择神经网络模型的输入因子，然后通过不同神经网络模型进行径流预测，并进行不同方案的比较，以期了解不同方法的优劣。

2 研究区概况及数据来源

2.1 研究区概况

喀什河流域位于天山西部，属于伊犁河的支流，整个流域全长约为304 km，面积约为9 541 km2。流域上仅有一个乌拉斯台水文站以及临近的尼勒克、伊宁气象站，基于站点1960—2005年的数据统计：流域的多年平均径流量为102.2 m3/s；多年平均降雨量为561.7 mm；春季最高气温为8.97 ℃，最低气温为3.03 ℃；夏季最高气温为18.33 ℃，最低气温为14.77 ℃；秋季最高气温为8.40 ℃，最低气温为3.40 ℃；冬季最高气温为-4.83 ℃，最低气温为-13.13 ℃；多年平均气温为5.39 ℃。

2.2 数据来源

借助水文数据、气象数据、探空数据等对研究区融雪为主河流的径流量进行中长期水文预报研究。数据主要来源如表1所示。

表1 数据来源Table 1 Sources of data

注：1 hPa= 100 Pa

太阳活动也影响着河川径流变化，因此收集北半球1960—2005年逐月的太阳黑子数作为预报的影响因子。表1中有13个影响因子，加上太阳黑子数合计为14个与研究区径流相关的影响因子。

3 预报因子的确定

3.1 互信息理论

互信息是一种信息度量，可以用来表示2个或多个变量之间的相关性，而且能反映变量间线性相关关系之外的非线性相关关系。如果变量X，Y互不相关，则X，Y的联合分布密度等于边缘分布密度之积，可表示为

pX,Y(x,y)=pX(x)pY(y) 。

(1)

式中：pX(x)为X的概率密度；pY(y)为Y的概率密度；pX,Y(y)为X与Y的联合分布密度。

给定N个离散观测样本，变量X，Y之间互信息计算公式为

(2)

式中MI为互信息量值。

由式(2)可知，当X与Y互不相关时，MI 取值将趋近于 0；当X与Y之间存在函数关系时，MI 取值将趋近于正无穷大。

若给定变量X的N个观测样本，其概率密度pX(xi)采用核函数(多维高斯分布密度函数)，进行估计，即

(3)

(4)

借助水文数据、气象数据和探空数据共14个相关因子水文序列分别计算与径流序列的互信息量值MI，结果如表2所示。

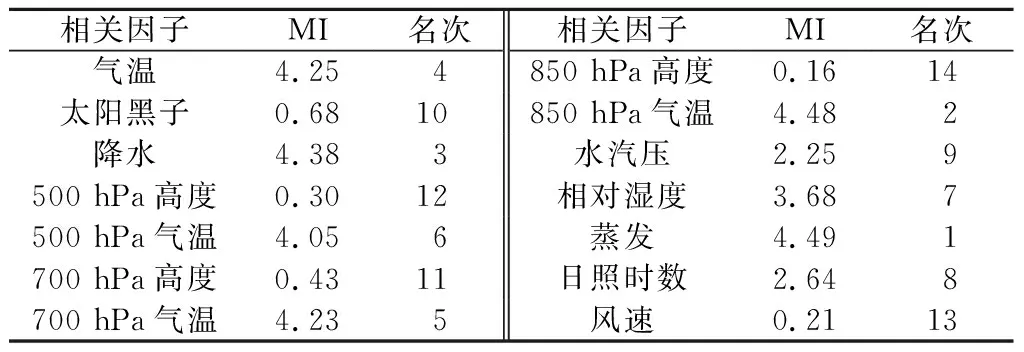
表2 预报因子与径流序列的互信息量值Table 2 Coefficient matrix of factor score with MI(mutual information)

表2包括14个相关因子与径流序列的互信息MI值以及所占名次(名次是MI值由大到小排序，即名次1为MI值最大所对应的因子)。由表2可见,蒸发、850 hPa气温、降水、气温、700 hPa气温、500 hPa气温这6个相关因子的MI值都>4，是14个相关因子中的前6名，也就是相关性最好的6个因子；相对湿度与径流序列的互信息MI值为3.68，是14个相关因子中的第7名，相关性较好仅次于第6名的MI值0.37。选取互信息MI值最好的7个相关因子(蒸发、850 hPa气温、降水、气温、700 hPa气温、500 hPa气温、相对湿度)作为预报模型的输入变量。

3.2 预报因子的挑选

目前对预报因子的挑选已有大量研究，本文选取以下挑选方法进行预测：

(1)全部预报因子法(全因子法)。借助水文数据、气象数据和探空数据共14个相关因子水文序列直接作为径流预测的预报因子。

(2)相关系数法。对选取的14个相关因子水文序列分别计算与径流序列的相关系数值，选取R2最大的前7个因子作为预报因子。

(3)主成分分析法。运用主成分分析法对14组相关因子数据进行主成分提取，提取出3组代表14个相关因子的主要成分X1，X2，X3。

(4)互信息法。借助互信息法计算14组预报因子与径流之间的互信息量值MI，选取MI最大的7个预报因子。

4种方法的具体因子见表3。

表3 乌拉斯台径流预报因子的优选结果Table 3 Optimized predictors for runoff at Wulasitai Station

4 实 例

本文通过相关系数法、互信息法及主成分分析方法进行预报因子的优选，确定出3组不同的预报因子与不进行因子挑选的全部因子(见表3)，将这4组数据作为模型的输入因子。并采用组合小波BP神经网络模型与RBF神经网络模型对径流序列进行预测。

4.1 不同神经网络预测模型

4.1.1 组合小波BP神经网络模型

以1960年1月—1999年12月逐月预报因子序列和径流序列作训练和测试数据， 2000年1月—2005年12月的径流序列作为检验数据，建立组合小波BP神经网络模型进行中长期水文预报研究。4种挑选方法的预测结果如图1，相对误差如表4。

图1 乌拉斯台站径流小波BP神经网络预测结果Fig.1 Runoff predictions for Wulasitai Station by wavelet BP neural network

年份与实测值的平均相对误差/%全因子法相关系数法主成分分析法互信息法2000-7.50-8.42-5.16-4.032001-12.90-3.53-9.89-1.422002-1.412.93-3.437.502003-7.46-12.99-13.83-10.552004-7.51-2.41-9.77-5.402005-19.51-6.75-11.16-13.48平均值-9.38-5.20-8.87-4.56

由图1可见：①4种挑选方法对径流量低值的预测效果都较好，高值预测都不太理想、拟合效果不好；②其中全因子方法的拟合效果最差，对于高值与低值的预测都出现较大的偏差；③互信息法不仅对径流量的高、低值的拟合效果在4种挑选方法里最好，而且整个径流过程的拟合程度也较高。因此由互信息法挑选出的预报因子建立的组合小波BP神经网络模型预测出的径流量与实测值最为接近。

由表4可以看出：①全因子的预测结果的相对误差为-19.51%～-1.41%，平均为-9.38%； ②相关系数法的预测结果的相对误差为-12.99%～2.93%，平均为-5.20%；③主成分分析法的预测结果的相对误差为-13.83%～-3.43%，平均为-8.87%；④互信息法的预测结果的相对误差为-13.48%～7.50%，平均为-4.56%；⑤互信息法在这6 a的平均相对误差最小，较全因子法少4.82%，较相关系数法少0.64%，较主成分分析法少4.31%，可作为组合小波BP神经网络预报模型的最优预报因子挑选方案。

4.1.2 RBF神经网络模型

分别采用全因子、相关系数法、主成分分析法和互信息法等方法确定的预报因子，具体见表3。以1960年1月—1999年12月逐月的预报因子序列和径流序列作为训练和测试数据， 2000年1月—2005年12月的径流序列作为检验数据，建立RBF神经网络模型进行中长期水文预报研究。4种挑选方法的预测结果如图2，相对误差如表5。

由图2可见：①4种挑选方法对径流量低值与高值的预测效果都较好；②其中全因子法和主成分分析法对高值的拟合效果较差；③互信息方法对径流量的高、低值的拟合效果在4种挑选方法里最好，整个径流过程的拟合程度也较高。因此由互信息方法挑选出的预报因子建立的RBF神经网络模型预测出的径流量与实测值最为接近。

图2 乌拉斯台站径流RBF神经网络预测结果Fig.2 Runoff predictions for Wulasitai Station by RBF neural network

年份与实测值的平均相对误差/%全因子法相关系数法主成分分析法互信息法2000-14.99-1.08-30.905.652001-5.564.16-22.107.352002-19.23-11.07-37.10-9.822003-5.33-5.26-28.92-3.032004-11.75-13.69-36.21-13.3320050.011.52-15.571.48平均值-9.48-4.24-28.47-1.95

计算出2000—2005年每年的平均相对误差(表5)可以看出：①全因子法预测结果的相对误差最大为-19.23%，最小为0.01%，平均为-9.48%；②相关系数法预测结果的相对误差为-13.69%～4.16%，平均为-4.24%；③主成分分析法的预测结果的相对误差为-37.10%～-15.57%，平均相对误差为-28.47%；④互信息法的预测结果的相对误差为-13.33%～7.35%，平均为-1.95%；⑤互信息法在这6 a的平均相对误差最小，相对于全因子法减少7.53%，相对于相关系数法减少2.29%，相对于主成分分析法减少26.52%，可作为RBF神经网络预报模型的最优预报因子挑选方案。

4.1.3 不同方案的预测结果分析

将各挑选结果分别作为2个神经网络模型输入数据，径流序列作为输出数据。得到不同预报结果的相对误差如表6所示，将互信息法作为最佳预报因子的挑选方法分别得到2个模型的预报结果如图3所示。

表6 不同方案下乌拉斯台站径流的预测结果Table 6 Runoff prediction errors for Wulasitai Station by different methods

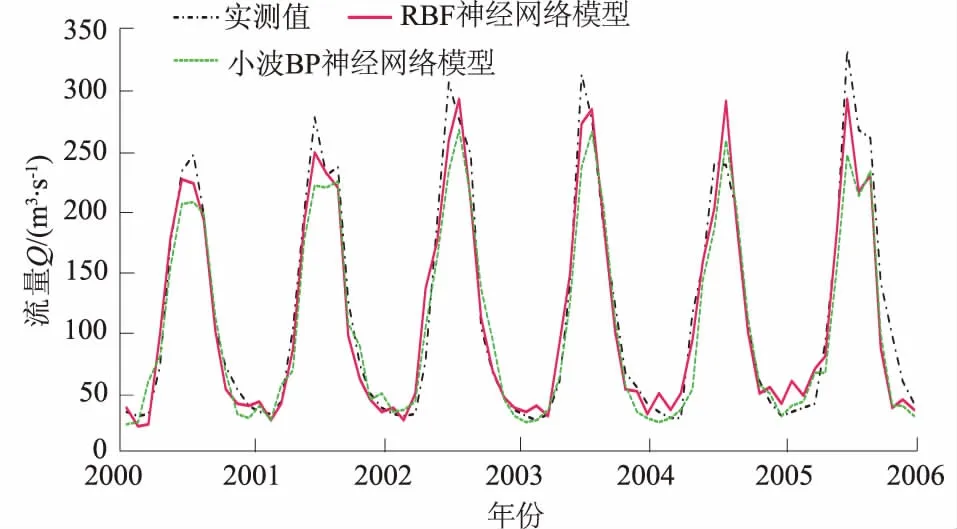
图3 乌拉斯台站径流预测结果Fig.3 Result of runoff predictions for Wulasitai Station

从表6可以看出,不同的输入数据对2种不同模型的预测结果都有影响。其中互信息方法挑选出的预报因子作为输入因子的预测效果要好于其他方法挑选预报因子作为输入数据的预测效果。在小波BP神经网络模型预测结果中,互信息法的预测结果平均相对误差相对于全因子法减少4.82%，相对于相关系数法减少0.64%，相对于主成分分析法减少4.31%。从图3中可以看出,RBF神经网络对径流高、低值及径流过程的拟合效果都比小波BP神经网络要理想。

5 结 论

基于相关系数法、互信息法和主成分分析法3种方法优选预报因子，以及全因子法得到4种不同的预报因子挑选结果。将这4种预报因子的挑选作为输入因子，径流数据作为输出因子对RBF神经网络和组合小波BP神经网络进行建模得到8种预测结果。可以看出：

(1)不同预报因子在神经网络模型中的预测结果都不同，不同预报因子挑选方法较不进行因子筛选的全因子法相比，其预报精度有着不同程度(0.51%～7.53%)的提高，因此在进行径流中长期预报中重视对预报因子的挑选，可以在一定程度上提高预测精度得到更高的合格率。

(2)互信息量可同时反映出预报因子与径流序列之间的线性关系和非线性关系，较相关系数法、全因子法、主成分分析法的预测结果，平均相对误差大大减少。在小波BP神经网络模型预测结果中，互信息法较其他方法的预报精度提高了0.64%～4.82%；在RBF神经网络模型预测结果中，互信息法较其他方法的预报精度提高了2.29%～26.52%。因此选用互信息量挑选预报因子作为模型输入可以提高模型的预报精度。

(3)以相对误差作为评价模型精确度的标准得到结果分析，基于互信息方法挑选出的预报因子作为RBF神经模型输入数据的模型预测精度最高，较互信息法结合小波BP神经网络模型的预测精度提高了2.61%，因此在天山西部山区该方法对径流中长期水文预报研究具有一定参考价值。

从模拟的结果来看，尽管预报模型在天山西部山区具有较好的适用性，但模拟径流值与实测径流值之间仍然存在一定的误差，所有的大误差都是出现在尖峰处，该误差可能来自预报因子的挑选方面，相关系数法只能挑选出与径流序列线性关系较好的因子，主成分分析法也只能挑选出因子的主要成分，即便是互信息方法对预报因子的挑选也存在不足，或者还有影响尖峰变化的因素没有考虑进去，对水文预报精度制约的关键因素是模型输入因子的确定。

在今后的研究中，如果能找到精度更好的挑选因子方法，或加入影响尖峰变化的因素，并充分考虑研究区的实际情况建立带有递归的动态神经网络模型，模型模拟精度可能会进一步提高，以期更好地指导所在区域融雪径流模拟研究与洪水预报方面的工作。