Weighted Sparse Image Classification Based on Low Rank Representation

Qidi Wu, Yibing Li, Yun Lin, and Ruolin Zhou

Abstract: The conventional sparse representation-based image classification usually codes the samples independently, which will ignore the correlation information existed in the data. Hence, if we can explore the correlation information hidden in the data, the classification result will be improved significantly. To this end, in this paper, a novel weighted supervised spare coding method is proposed to address the image classification problem. The proposed method firstly explores the structural information sufficiently hidden in the data based on the low rank representation. And then, it introduced the extracted structural information to a novel weighted sparse representation model to code the samples in a supervised way. Experimental results show that the proposed method is superiority to many conventional image classification methods.

Keywords: Image classification, sparse representation, low-rank representation,numerical optimization.

1 Introduction

Image classification is a fundamental issue in computer vision, which aims to classify an image into an accurate category. Many literatures about image classification are emerged in the past two decades [Liu, Fu and He (2017)], and several classification frameworks are formed to address the classification problem of vision task. During the mentioned frameworks, sparse-based classification attracted many attentions and are widely studied in recent years. Sparse signal representation has proven to be an extremely powerful tool for acquiring, representing, and compressing high-dimensional signals [Wright, Ma,Mairal et al. (2010)]. In the past few years, sparse representation has been applied to many vision tasks, including face recognition [Yang, Zhang, Yang et al. (2011); Liu, Tran and Sang (2016)], image super-resolution [Yang, Chu and Wang (2010); Yang, Wright,Huang et al. (2010)], denoising and inpainting [Fadili, Starck and Murtagh (2013);Guleryuz (2006)], and image classification [Kulkarni and Li (2011); Thiagarajan and Spanias (2012)]. Due to its wide applicability, people conducted detailed research on image classification based on sparse representation and achieved remarkable results[Tang, Huang and Xue (2016); Gao, Tsang and Chia (2010); Liu, Fu and He (2017)].According to the picture type, image classification is mainly applied in certain specific fields such as face recognition and hyperspectral image classification and remote sensing image classification. In face recognition, based on a sparse representation computed by l1-minimization, Wright et al. [Wright, Ma, Mairal et al. (2010)] proposed a general classification algorithm for (image-based) object recognition [Wright, Ganesh, Zhou et al.(2009)]. This new framework provided new insights into two crucial issues in face recognition: feature extraction and robustness to occlusion. The theory of sparse representation helped predict how much occlusion the recognition algorithm could handle and how to choose the training images to maximize robustness to occlusion. Recent research has shown the speed advantage of extreme learning machine (ELM) and the accuracy advantage of sparse representation classification (SRC) in the area of image classification. In order to unify such mutual complementarity and thus further enhance the classification performance, Cao et al. [Cao, Zhang, Luo et al. (2016)] proposed an efficient hybrid classifier to exploit the advantages of ELM and SRC in Cao et al. [Cao,Zhang, Luo et al. (2016)]. While the importance of sparsity is much emphasized in SRC and many related works, the use of collaborative representation (CR) in SRC is ignored by most literature. This paper [Zhang, Yang and Feng (2011)] devoted to analyze the working mechanism of SRC, and indicated that it was the CR but not the l1-norm sparsity that made SRC powerful for face classification. The authors proposed a very simple yet much more efficient face classification scheme, namely CR based classification with regularized least square (CRC_RLS), which had very competitive classification results, many classic and contemporary face recognition algorithms work well on public data sets, but degrade sharply when they are used in a real recognition system. This is mostly due to the difficulty of simultaneously handling variations in illumination, image misalignment, and occlusion in the test image. Considering this problem, Wagner et al. [Wagner, Wright, Ganesh et al. (2012)] proposed a conceptually simple face recognition system that achieved a high degree of robustness and stability to illumination variation, image misalignment, and partial occlusion. Besides, Zhang et al.[Zhang, Zhang, Huang et al. (2013)] proposed a pose-robust face recognition method to handle the challenging task of face recognition in the presence of large pose difference between gallery and probe faces. The proposed method exploited the sparse property of the representation coefficients of a face image over its corresponding view-dictionary. In hyperspectral image classification, Tang et al. [Tang, Chen, Liu et al. (2015)] present a hyperspectral image classification method based on sparse representation and superpixel segmentation. By refining the spectral classification results with the spatial constraints,the accuracy of classification is improved by a substantial margin in Tang et al. [Tang,Chen, Liu et al. (2015)]. Noting that the structural information can earn some extra discrimination for the classification framework [Liu, Fu and He (2017)], some methods considering the structural and contextual information are presented. A new sparsity-based algorithm for the classification of hyperspectral imagery was proposed in Chen et al.[Chen, Nasrabadi and Tran (2011)], which relied on the observation that a hyperspectral pixel could be sparsely represented by a linear combination of a few training samples from a structured dictionary. They mainly used Laplacian constraint and joint sparsity model to incorporate the contextual information into the sparse recovery optimization problem in order to improve the classification performance. To overcome this problem that the sparse representation-based classification (SRC) methods ignore the sparse representation residuals (i.e. outliers), Li et al. [Li, Ma, Mei et al. (2017)] proposed a robust SRC (RSRC) method which could handle outliers. They extended the RSRC to the joint robust sparsity model named JRSRC, where pixels in a small neighborhood around the test pixel were simultaneously represented by linear combinations of a few training samples and outliers. A superpixel tensor sparse coding (STSC) based hyperspectral image classification (HIC) method is proposed, by exploring the high-order structure of hyperspectral image and utilizing information along all dimensions to better understand data in Feng et al. [Feng, Wang, Yang et al. (2017)]. Article [Sun, Qu, Nasrabadi et al.(2014)] proposes a new structured prior called the low-rank (LR) group prior, which can be considered as a modification of the LR prior. Structured Priors for Sparse-Representation-Based Hyperspectral Image Classification. The paper [Zhang, Song, Gao et al. (2016)] presents a new spectral–spatial feature learning method for hyperspectral image classification, which integrates spectral and Zeng et al. [Zeng, Li, Liang et al.(2010)] spatial information into group sparse coding (GSC) via clusters and propose a novel kernelized classification framework based on sparse representation considering the image classification problem based on the similarities between images [Zhang, Zhang,Liu et al. (2015)]. Article [Zeng, Li, Liang et al. (2010)] proposes a fast joint sparse representation classification method with multi-feature combination learning for hyperspectral imagery and incorporate contextual neighborhood information of the image into each kind of feature to further improve the classification performance. The paper[Wang, Xie, Li et al. (2015)] investigates STDA (Sparse Tensor Discriminant Analysis)for feature extraction and it is the first time that STDA is applied for HIS (Hyperspectral imagery) and attempts to adopt STDA to preserve useful structural information in the original data and obtain multiple interrelated sparse discriminant subspaces. In remote sensing image classification，The paper [Shivakumar, Natarajan and Murthy (2015)]presents a novel multi-kernel based sparse representation for the classification of Remotely sensed images. The sparse representation based feature extraction are in a run which is a signal dependent feature extraction and thus more accurate. The paper [Song,Li, Dalla et al. (2014)] proposes to exploit sparse representations of morphological attribute profiles for remotely sensed image classification. By using the sparse representation classification framework to exploit this characteristic of the EMAPs.

With more and more sources of image data on the Internet, images are becoming more and more cluttered, making more and more images lack complete category information.Based on this, the researchers proposed semi-supervised and unsupervised image classification methods. To address the problem of face recognition when there is only few,or even only a single, labeled examples of the face that we wish to recognize. The main idea was that: they used the variation dictionary to characterize the linear nuisance variables via the sparsity framework and prototype face images were estimated as a gallery dictionary via a Gaussian mixture model, with mixed labeled and unlabeled samples in a semi-supervised manner, to deal with the non-linear nuisance variations between labeled and unlabeled samples. Unsupervised learning methods for building feature extractors have a long and successful history in pattern recognition and computer vision. Document [Huang, Boureau and Le (2007)] proposes an unsupervised method to learn the sparse feature detector hierarchy, which is invariant for small shifts and distortions. Article [Zeiler, Krishnan, Taylor et al. (2010)] present a learning framework where features that capture these mid-level cues spontaneously emerge from image data and the approach is based on the convolutional decomposition of images under a sparsity constraint and is totally unsupervised. The paper [Poultney, Chopra and Cun (2007)]describes a novel unsupervised method for learning sparse, overcomplete features. The model uses a linear encoder, and a linear decoder preceded by a sparsifying non-linearity that turns a code vector into a quasi-binary sparse code vector. The major contribution of paper [Hassairi, Ejbali and Zaied (2016)] is to show how to extract features and train an image classification system on large-scale datasets.

In this paper, we proposed novel sparse representation-based image classification with weighted supervision sparse coding. It firstly constructed the supervision coefficient with Low rank representation, which would help to mine the structural information hidden in the data. And then, the supervision coefficient is incorporated into a weighted sparse representation framework to preserve the coding structure of similar samples. It is verified that the proposed method shows some advantage on the public test dataset.

The remaining of the paper is arranged as follows. In section II, several similar previous works are analyzed. In section III, the proposed method is described in detail. In section IV, the experimental results are shown to demonstrate the superiority of the proposed method. Section V concludes the paper.

2 Related work

Although the traditional spatial pyramid matching (SPM) approach works well for image classification, people empirically found that, to achieve good performance, traditional SPM has to use classifiers with nonlinear Mercer kernels. Accordingly, the nonlinear classifier has to afford additional computational complexity, bearing O(n3) in training and O(n) for testing in SVM, where n is the number of support vectors. This implies a poor scalability of the SPM approach for real applications.

To improve the scalability, researchers aim at obtaining nonlinear feature representations that work better with linear classifiers

Let X be a set of D-dimensional local descriptors extracted from an image,i.e. X =[x1, x2,...,xN]∈RD×N. Given a codebook with M entries, B =[b1, b2,...,bM]∈RD×M,different coding schemes convert each descriptor into adimensional code to generate the final image representation. This section reviews three existing coding schemes.

2.1 Coding descriptors in VQ

Traditional SPM uses VQ coding which solves the following constrained least square fitting problem:

where C =[c1, c2,...,cN]is the set of codes for X. The cardinality constraintci0=1 means that there will be only one non-zero element in each code ci, corresponding to the quantization id of xi.The non-negative,1constraint ci1= 1,ci≥0means that the coding weight for x is 1. In practice, the single non-zero element is found by searching the nearest neighbor.

2.2 Coding descriptors in ScSPM

To ameliorate the quantization loss of VQ, the restrictive cardinality constraint=1 in Eq. (1) can be relaxed by using a sparsity regularization term. In ScSPM [Yang, Yu,Gong et al. (2009)], such a sparsity regularization term is selected to be the1norm of ci,and coding each local descriptorxithus becomes a standard sparse coding (SC) [Lee,Battle, Raina et al. (2007)] problem:

The sparsity regularization term plays several important roles: First, the codebook B is usually over-complete, i.e.M＞D, and hence1regularization is necessary to ensure that the under-determined system has a unique solution ; Second, the sparsity prior allows the learned representation to capture salient patterns of local descriptors; Third, the sparse coding can achieve much less quantization error than VQ. Accordingly, even with linear SVM classifier, ScSPM can outperform the nonlinear SPM approach by a large margin on benchmarks like Caltech-101 [Yang, Yu, Gong et al. (2009)].

2.3 Coding descriptors in LLC

Locality-constrained Linear Coding (LLC) was presented by Wang et al. [Wang, Yang,Yu et al. (2010)]. LLC incorporates locality constraint instead of the sparsity constraint in Eq. 2, which leads to several favorable properties, including better reconstruction, local smooth sparsity and analytical solution. Specifically, the LLC code uses the following criteria [Yuan, Ma and Yuille (2017)]:

With the above description of LLC coding, we can see that the locality constrain will earn extra discrimination for the coding coefficients. Because, some structure information is introduced the coding by enforcing some coefficients with weak sample correlation to be zero, which will help to select more samples within the same subspace. Next, we will proposed a weighted sparse classification framework to improve the coding structure.And then, to explore the supervision information hidden in the data, a novel supervision constraint item about coding approximation are also proposed as the part of the weighted sparse classification framework.

3 Sparse image classification model based on low-rank supervision

3.1 Low-rank representation model

Low-rank matrix recovery is the development and promotion of the compressive sensing theory, using the rank as a measure of the matrix sparseness. The low-rank representation model has well capable of handling high-dimensional signal data. The model can be used to recover damaged observational samples and can find low-dimensional feature space from noisy samples. A matrix representation of the image data, the original observation data matrix X ∈Rm×nand the model that uses the rank of matrix for sparse representation is as follows:

If the sample matrix X exists in several low-dimensional spaces, the sample matrix X can be linearly represented by a set of low-dimensional space bases A, that is, the sample itself is selected as the dictionary, the lower rank represents the coefficient matrix Z, and the Z represents each data vector The weight of a linear combination. A low-rank constraint on the coefficient Z results in a low-rank representation of the sample matrix X as follows:

which is a non-convex optimization problem. In the solution, we usually apply convexrelaxation method and replace rank( Z)with the matrix kernel function. The following formula:

In practical applications, the signal is likely to be polluted by noise, so the above equation can be further expressed as:

In recent years, researchers have proposed many efficient optimization algorithms to solve the above problems, such as Iterative Thresholding, Exact Augmented Lagrange Multiplier, Inexact Augmented Lagrange Multiplier and so on. These algorithms can learn fromminimization, the following describes the Exact and Inexact Augmented Lagrange Multiplier algorithm. Before that, we need Augmented Lagrange Multiplier (ALM) algorithm.

The objective function for a constrained optimization problem can be described by:

where Y is Lagrange multiplier. μis known as the penalty coefficient that is a positive number.is inner product operator. When the values of Y and µare appropriate, the objective function can be solved by Augmented Lagrange algorithm. Asume thatThe Eq. (11) can be expressed by this:

which can be solved by using alternate ways to optimize the update. Let Y andbe fixed values solving minimized L to obtain A . Then fix Y and A, and solve for minimized Lto obtain E. It is done iteratively until the convergent solution is eventually obtained that is called the Exact Augmented Lagrange Multiplier method.Since Aand E are coupled to each other in Eq. (12), each iteration will be placed in the same sub-problem during the iteration, which makes the solution feasible. In practice the Exact Augmented Lagrange Multiplier method requires multiple iterations, so the algorithm runs at a lower speed. On the basis of the former, an Inexact AugmentedLagrange Multiplier method is proposed, in which the A and are updated once at each iteration to obtain the approximate solution of the sub-problem.

Figure 1: Ideal structure of the coefficient matrix in SRC

The core idea based on sparse representation is that the test sample is expressed by a linear combination of training samples. Because most non-zero elements have the same base corresponding to the test sample. In ideal case, we expect each sample to be in its own category subspace and all the category subspaces do not overlap. Specifically, given a category of images recorded as C and dictionaries D =[D1,...,DC]which DCcontains training samples from the category c=1,...,C. That is meaning that a new sample y belonging to the category c can be represented byis a representation coefficient under a sub-dictionary Dc. So we can use the dictionary D to represent y :Most of the valid elements should be located in ac,so the coefficient vector acshould be sparse. From vector to matrix form,Y =[Y1,...,Yc,...,YC]is the entire sample set matrix containing the category samples, the coefficient matrix Awill be also sparse, and in the ideal case the matrix Ais a block diagonal matrix as shown in Fig. 1.

3.2 Correlation matrix construction

Assume that the test sample matrix Y =[y1, y2,...,yn], yndenotes the no.test sample vector. Based on above analysis, we can use the sample as a dictionary and use the matrix Zto explore the correlation between samples to obtain the low-rank representation model of the test sample as follows:

3.3 Sparse image classification model based on low-rank supervision

To make better use of correlations between samples and obtain feature representationswith better discrimination capability, we use the low-rank representation matrix to perform low-rank supervision constraints on the sparse coding process and propose a new low-rank supervised sparse coding model.

First, we can obtain a supervisory matrix from a low-rank representation matrix, as shown in the following equation:

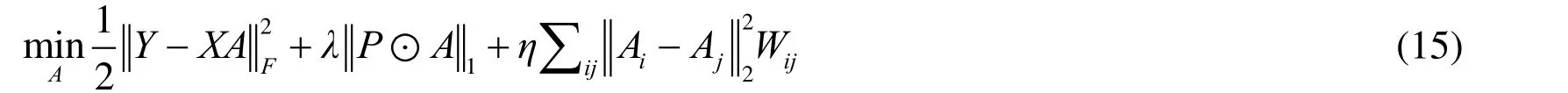
where A is feature representation matrix, λand ηare regularization parameters. In the above model, we have added the supervision constraint itemto increase the difference in coding between different categories, where i and jare the column numbers of the feature representation matrixA . Pis the correlated weighted for the sparse coefficient.denotes the element-wise multiplication operator. Wijis used to represent the elements of the row i and column jin the supervising matrix W. By solving the model 10, we can get the representation matrix A with stronger discrimination ability.

After obtaining the feature representation matrixA , the reconstruction error can be used to classify and the classification model as follows:

Acorresponding to the ith sample. Find the Eq. (16) to minimize the reconstruction error label is the classification result, that is the formula for the minimum value of k.

4 Solving the sparse image classification model based on low-rank supervision

This section describes the process of solving the above low-rank supervised coding model in detail. The model 10 can be transformed as follows:

Eq. 17 is a non-convex problem. We can make an equidistant transformation to get the following based on

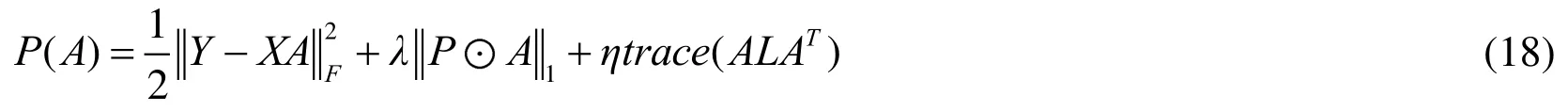
where trace()is trace of matrix, L is lagrange operator and L=D− W . The matrixis a diagonal matrix whose elements on the diagonal correspond to the sum of all elements of the column vector in the matrix W , namelyand jare the row and column numbers of the matrix. This problem is transformed into a convex optimization problem.

For the optimization solution, we can get the gradient solution formula of G( A)as follows:

where ∇is a gradient indicator. According to Eq. (19) and Eq. (20), the iterative shrinking algorithm can be used to solve the original model (17), which iterative solution is as follows:

As for the Eq. (21), it is a typical weighted l1-norm minimization problem, which can be solved with the numerical method in Guleryuz [Guleryuz (2006)]. And then, we can obtain the feature representation matrix A and use the classification model shown in model (16) to classify images.

5 Experimental results and analysis

5.1 Experimental data

For the weighted sparse image classification method based on low-rank representation proposed in this paper, we take the ORL and COIL-20 image datasets as the experimental datasets.

Figure 2: Two groups of face samples of ORL dataset

The ORL face dataset contains 400 face images, which were shot by 10 people under different lighting conditions, varying view and expressions. Each person has about 10 face images. Fig. 2 shows some face samples of the ORL dataset.The COIL-20 image dataset is collected by Columbia Object Image Library, which contains images of 20 items. During shooting the image, the object is placed on a rotating plate with black background. Through the 360 degree rotation of the plate to change the attitude of the item relative to the camera. Each object in the dataset has 72 images with different angles, and some examples are shown in Fig. 3.

Figure 3: Example images of COIL-20 database

In the experiment, we implemented the sparse representation-based image classification methods SRC, CRC, LRSRC on the above two public datasets. The algorithm proposed in this paper is compared to verify.

5.2 Comparison and analysis of experiments

First of all, in order to verify the validity of the method proposed in this chapter, we use the ORL face image data set to display, and visualize the obtained low-rank representation matrix and its corresponding feature representation matrix. The low-rank representation matrix is shown in Fig. 4, and the characteristic representation matrix is shown in Fig. 5.From these two figures, it can be observed that the representation matrix has a distinct diagonal block structure, indicating that the representation matrix should theoretically have the discriminative ability of classification, the experimental result of the latter also confirmed this prediction. From the comparison of these two graphs, we can also find that compared with the low rank representation matrix, the elements in the diagonal matrix of the representation matrix are enhanced after being coded from the supervision limit to make it have a more obvious diagonal block structure, indicating better class resolution.

Figure 4: Visualization of low-rank representation matrix for ORL

Figure 5: Visualization of sparse representation matrix for ORL

We performed simulation experiments on the above methods in the Extended YaleB face image dataset and COIL-20 image dataset and obtained the corresponding experimental results. We test five times for each method, and take the average accuracy as the final result, which is shown in Tab. 1. The number shown in the parentheses denotes the number of training samples.

Table 1: Average accuracy of each classification method

From Tab. 1, we can see that our proposed method shows higher accuracy classification result on all the experimental datasets over the comparison methods. It is verified that the weighted sparse coding with the low rank supervision can greatly improve the structure of coding to be more discriminative.

6 Summary

On the basis of the SRC method, this paper proposes a weighted sparse image classification method based on low-rank supervision. The proposed one strengthens the sample discrimination ability of the feature representation matrix, which makes full use of the correlation between samples to weighted code the image sparsely. Different types of sparse represent the degree of coding discrimination, which is believed to improve the accuracy of image classification. We replace the non-convex terms in the model equivalently, use the iterative shrinking algorithm to solve and verify the correctness through some experiments. Compared with related conventional classification methods,the method proposed in this paper is better than them.

Acknowledgement:This research is funded by the National Natural Science Foundation of China (61771154).