“一带一路”下基于两阶段模型的无水港选址研究

梁承姬 黄博峰

(上海海事大学物流研究中心 上海 201306)

0 引 言

2013年，中国提出亚欧经济整合的蓝图，即 “一带一路”。“一带一路”的提出，一方面加快了我国中西部运输基础设施的建设，另一方面促进了我国与亚洲、欧洲之间运输业的发展。“一带一路”建设目前处于起步阶段，要实现亚欧运输的一体化需要考虑多式联运的有效对接。无水港作为其中重要一环，日益受到人们的重视。

国内外学者对“一带一路”和无水港/枢纽港已有诸多研究。蒋雪莹等[1]结合“一带一路”背景下的中欧铁路运输体系，考虑顾客的选择行为和基础设施处的拥挤与等货效应，建立了混合整数规划模型，解决了社会福利最大化时的铁路货运集拼中心的最优选址。高亚平[2]在明确了一带一路的运输网络后进行了环路分析，建立了运输费用模型，找出中国至各个路段的经济路线。文献[3]提出了一种评估无水港选址优先权的新方法，通过考虑反馈和影响无水港设施的因素建立评估模型，解决了无水港选址优先权评估问题；邵静静[4]基于评价指标体系方法，通过建立无水港选址多目标模型解决无水港选址问题；王莹等[5]通过建立无水港发展潜力评价指标体系，运用模糊层次分析法评价晋江无水港发展潜力；文献[6] 通过建立两级加权动态图的数学规划模型，解决了无水港在多式联运下集装箱流运输问题；文献[7]认为无水港在多式联运系统中存在优化的空间，提出了混合整数规划模型，解决了无水港联运系统中车辆运输的最佳路线和调度问题；梁承姬等[8]提出在集装箱多式联运的基础上，加入了成本折扣系数，并用改进遗传算法求解无水港选址问题。

综上可知，已有研究文献多数是基于评价指标体系或是选址优化的独立研究，没有考虑将两种研究方法结合为一体。据此，本文将这两种方法相结合，提出两阶段模型的无水港选址以及相应的求解方法，使无水港选址考虑因素更全面、科学。第一阶段借助模糊C-均值聚类分析选出候选城市，第二阶段在候选城市中进行选址优化，得出最优的选址结果。为验证两阶段模型的有效性，同时，本文又直接用单一的选址优化模型对算例进行求解，并将两者的求解结果对比，证明本文使用的方法更加有效。

1 问题描述

无水港根据距离依托母港的远近，可以分为近距离、中距离、远距离无水港。本文研究的是远距离无水港选址问题。假设在中欧、中国-中亚这两条支线的运输路线附近有众多的货源城市，这些货源城市需要将货物运往中国的某个沿海母港，如图1所示。独立地将货源城市的货物运往目的地会耗费较大的运输成本，而众多城市货物的联合运输可以产生聚集效应，降低成本，因此可以考虑在众多的货源城市中选择合适的城市建立无水港。本文考虑了货物的多式联运，联合运输中无水港作为衔接多种运输方式的中转站，通过其选址和运输方式选择的决策，可降低联合运输的成本、提高运输效率。

图1 运输路线图

综合考虑以上问题描述，通过建立两阶段模型解决上述问题。第一阶段根据一系列影响因素对货源城市的发展现状和潜力进行评估和筛选，选出适合作为无水港候选的城市。第二阶段，在上一阶段的基础上，通过建立包括运输成本、无水港建设成本、换装成本的总成本最小的目标函数，找出成本最低的无水港位置。

2 阶段1——候选无水港筛选模型

2.1 无水港选址评价指标体系

本节在综合考虑影响选址决策的整体因素及成功无水港必备条件的基础上，为筛选候选城市建立指标评估体系包括定性和定量指标，具体指标因素见表1所示。

其中交通拥挤度(x7)的指标从0～10, 指数在0～2为畅通、2～4为基本畅通、4～6为轻度拥堵、6～8中度拥堵、8～10为严重拥堵。政策倾向(x8)表示政府的支持倾向，1为支持，0为否。

2.2 评估求解方法

本文采用的FCM方法常用于具有较多影响因素以及影响未确定的目标进行聚类，对处理具有不确定性和模糊性的无水港评估因素具有优势。

本文假设有n个货源城市(x1,x2,…,xk,…,xn)根据指标p被聚类成c(2≤c≤n)个子集，FCM的目标是最小化非相似性目标函数J(U,V)。

(1)

约束条件：

(2)

式中：J表示FCM的目标函数；U表示隶属度矩阵集合；V表示聚类中心集合；dik表示xk与聚类中心的子集i的距离，即dik=‖xk-vi‖；m表示权重指数。

特别地，FCM主要分为以下六步：

步骤1: 确定类别c和加权指数m的数量。

步骤2: 通过从[0,1]中选择统一的数，初始化隶属度矩阵U(0)=(uik(0))。

步骤3: 计算聚类中心vl，公式如下：

(3)

步骤4: 修正隶属度矩阵U(l)并计算J(l)，公式如下：

(4)

(5)

dik=‖xk-vi‖

(6)

3 阶段2——无水港选址模型

本节将无水港选址优化问题转化为多式联运的物流运输网络问题来解决, 如图2所示。运输方式分为两种:第一种是直接从货源城市运往母港，即货源城市-母港；第二种是途经无水港，即货源城市-无水港-母港。本节考虑了多式联运，从货源城市运往母港的货物可能会发生分离，通过不同的运输方式或途经不同的无水港到达母港。同时，一个货源城市的货物可能会分离运往不同的无水港。

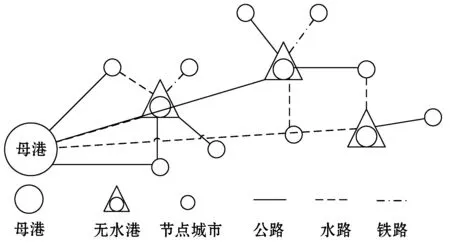
图2 途经无水港的多式联运

3.1 模型假设及参数符号说明

无水港选址模型假设如下：

1) 物流运输网络中每个货源城市都有三种运输方式可供选择：公路、铁路、水路；

2) 每段运输只能选择一种运输方式；

3) 货源城市数量、货物运输需求已知；

4) 运输费率、运输距离及转换费率已知；

5) 无水港建设成本已知,无水港个数定为4；

7) 货物到达无水港后换装时产生的等待时间忽略不计。

基于模型假设，构建无水港选址模型如下：

目标函数：

(7)

约束条件：

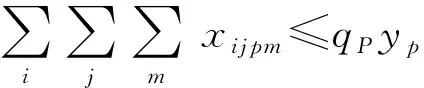
(8)

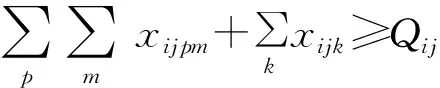
(9)

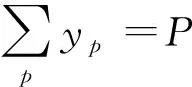
(10)

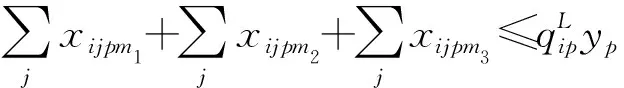
(11)

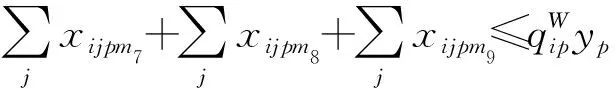
(13)

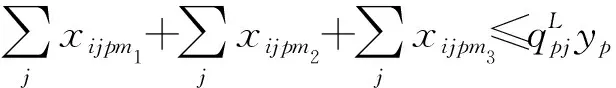
(14)

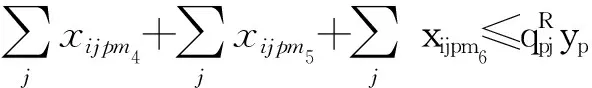
(15)

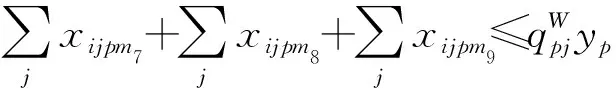
(16)

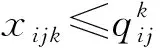
(17)

xijpm≥0 ∀i∈OS∀j∈OD∀p∈OPm∈M

(18)

yp∈{0,1} ∀p∈OP

(19)

3.2 遗传算法求解

该模型的离散决策变量代表无水港的容量约束和选址。本文提出以下有效的全局寻优方法，即遗传算法，以获得该模型最优解。

1) 编码 染色体用三段式的编码方法来描述选址。第一段采用二进制编码，表示是否选择候选货源城市作为无水港，1表示选该城市作为无水港候选，0表示未被选中。第二段表示第一段中城市的对应分配关系，若城市i分配给无水港p，则基因位值为p。第三段表示对应每个城市的运输方式，1、2、3、4、5、6分别表示上文提到的m1、m2、m3、m4、m5、m6。

下面以表2为例。染色体第一段中，1表示该在节点建立无水港，0表示该节点不建无水港，在节点2、6、8、13建立无水港；第二段的分配关系：节点1、3、7、10、11、14→母港，节点2、9→无水港(节点)2→母港，节点5、6→ 无水港(节点)6→母港，节点8→水港(节点)8→母港，节点12、13→无水港(节点)13→母港。第三段中，节点1、3、7、10、11、14分别以m6、m2、m4、m9方式直接运到母港，其余分别以对应方式运输，比如：节点2通过m3方式运输，节点9通过m1方式运输。

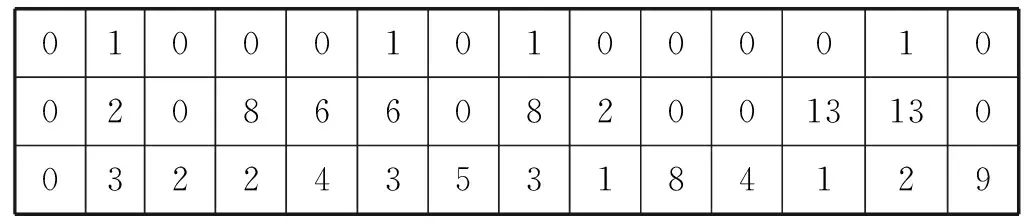
表2 染色体编码

2) 适应度函数 适应度函数被定义为目标函数的倒函数，即：

(20)

3) 选择操作 运用随机遍历的的方法，并综合运用最优保优策略。

4) 交叉操作 本文采用基于位置的交叉方法。子代C1、C2、C3得到父代P2、P1、P3的第一个n1基因，下一个n2-n1基因分别从P1、P3、P2得到，其余的|N|-n2基因分别从P3、P2、P1得到。图3说明了第一段染色体片段的交叉过程，其余两段操作同理。

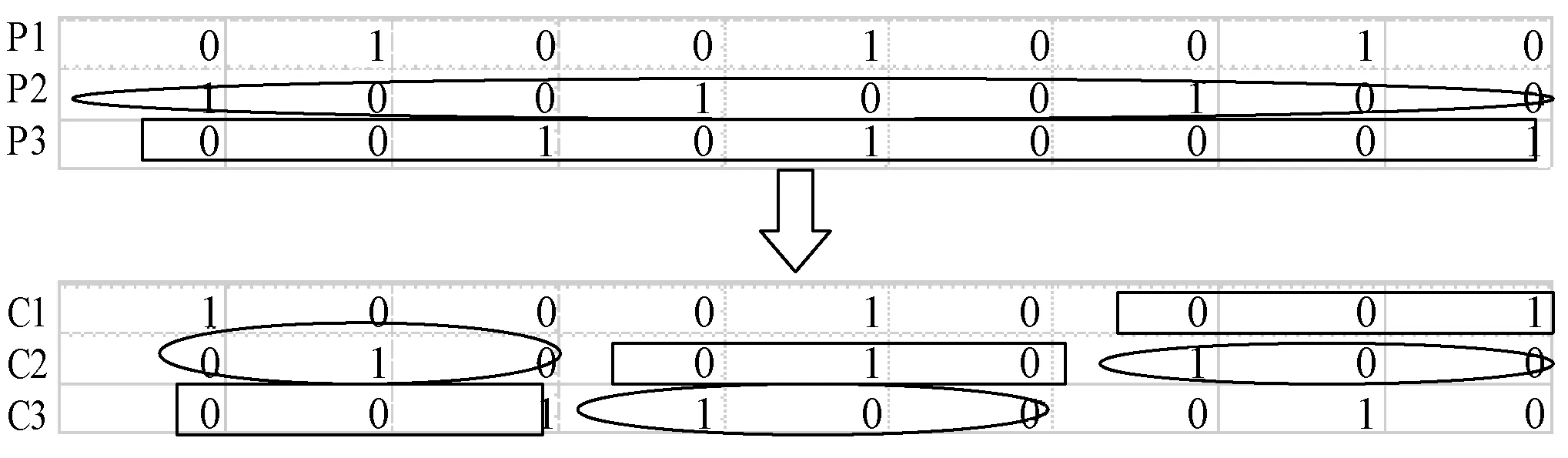
图3 交叉操作示意图

5) 变异操作 在满足无水港和路径容量约束的情况下，随机将两个城市对换。此处选取染色体的第一段，应用均换位异策略进行变异操作，如图4所示。

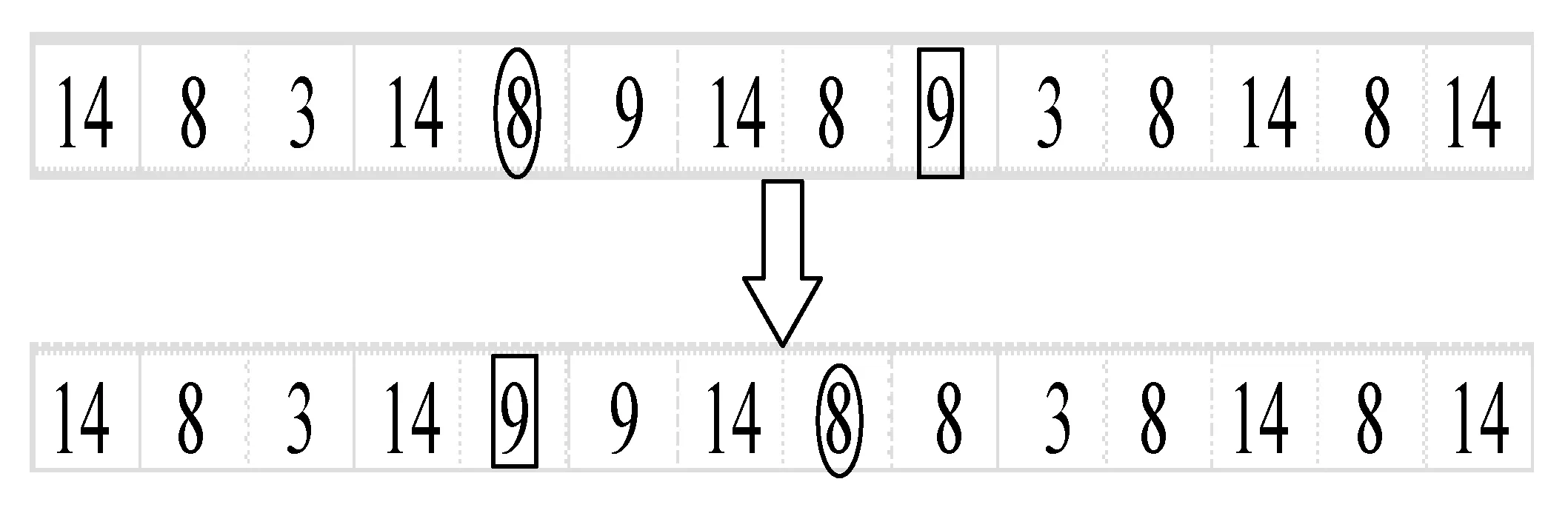
图4 变异操作示意图

6) 终止原则 当代数超过最大迭代代数时，算法终止。

4 算例分析

本文以上海港为母港，紧密联系“一带一路”经济走廊，以中国-中亚-欧洲这条主线上的货源城市为备选研究对象，优先考虑区域经济较发达地区，因此选取了苏州(1)、杭州(2)、郑州(3)、西安(4)、兰州(5)、呼和浩特(6)、敦煌(7)、乌鲁木齐(8)、杜尚别(9)、撒马尔罕(10)、多哈(11)、伊斯坦布尔(12)、莫斯科(13)、安曼(14)、圣彼得堡(15)、安卡拉(16)、德黑兰(17)、柏林(18)、杜伊斯堡(19)、法兰克福(20)、巴黎(21)、马赛(22)、耶路撒冷(23)、哥本哈根(24)这24个城市进行两阶段的无水港选址问题研究。

4.1 阶段1——候选无水港筛选

在本阶段中，选取了24个城市作为无水港候选城市。模型的参数假设设置如下：

1) 城市被分成4类，即c=4；

2) 基于聚类有效性分析，加权指数m=2；

3) 终止公差为：εu=1e-6。

FCM通过MATLAB的聚类分析，可以得到24个城市的Cluster Centre以及Cluster Membership，计算数据如表3、表4所示。

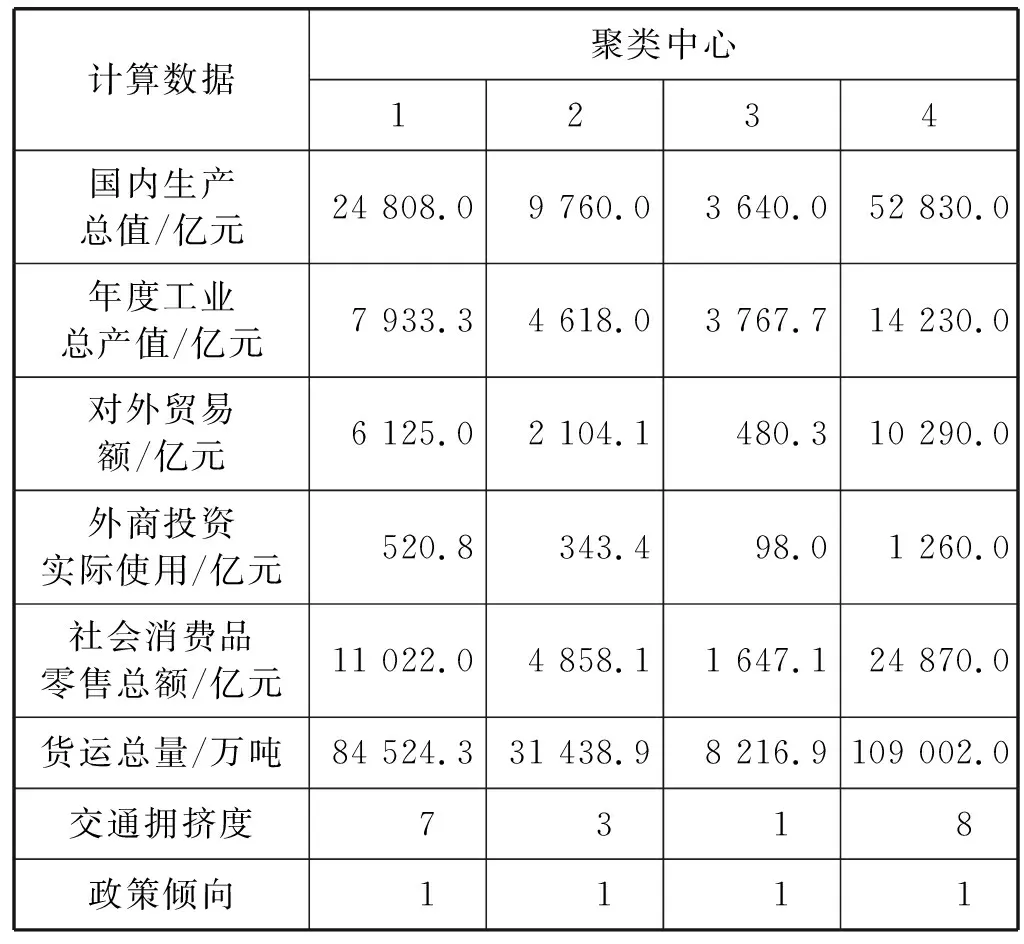
表3 最终聚类中心

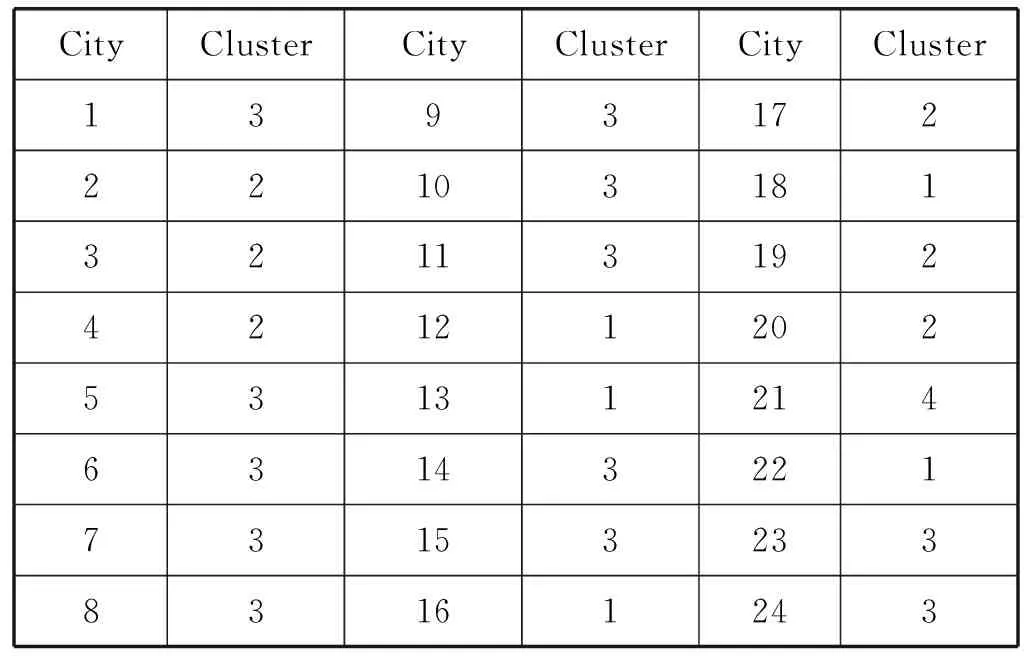
表4 聚类隶属度

表4结果表明，类别1有4个城市、类别2有7个城市、类别3有12个城市、类别4有1个城市。类别1代表最发达的城市，最适合作为无水港的选址。由于发达城市的交通拥堵，也应该考虑类别2中的城市。同时，由于欠发达城市的建设成本低，交通便利,在中国、中亚、欧洲这三个地区各再选一个，即在类别3选三个城市作为无水港选址。因此，获得14个城市作为潜在无水港的选址。最后,在第二阶段中做进一步研究，这14个城市包括苏州、杭州、郑州、西安、伊斯坦布尔、莫斯科、安曼、安卡拉、德黑兰、柏林、杜伊斯堡、法兰克福、马赛、哥本哈根。

4.2 阶段2——无水港选址

本阶段将第一阶段中最终选出的14个城市为候选城市，并以其作为无水港备选节点进行研究，上海港(0)为母港。通过分析这14个城市周边产业及经济情况，确定其货运量分别为：370 000吨，500 000吨，400 000吨，50 000吨，250 000吨，360 000吨，645 000吨，45 000吨，40 000吨，40 000吨，4 560吨，356 300吨，42 100吨，47 300吨。表5、表6给出了备选城市的相关数据，由于数据量大，故仅给出部分数据。由于各国的运输标准存在差异，统一采用中国标准：铁路运费0.3元/吨公里，水路运费0.2元/吨公里；公路换装1.8元/吨，铁路换装2.1元/吨，水路换装2元/吨。

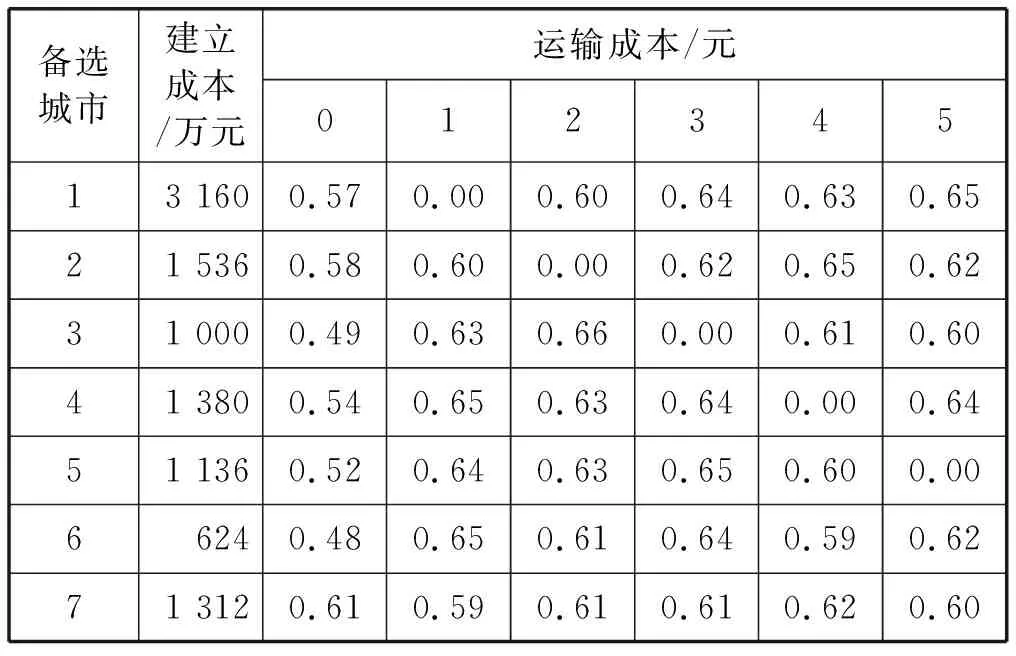
表5 无水港建立成本以及城市之间通过公路运输的货物单位运输成本

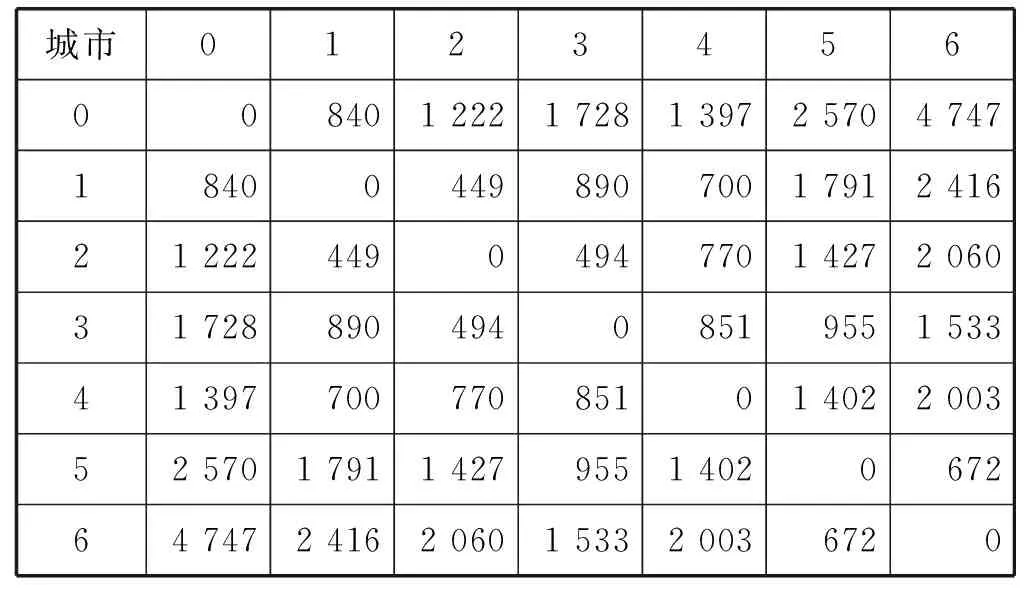
表6 城市与城市之间的距离 km

模型的参数输设置如下：

种群规模popsize=200，最大迭代次数MAXGEN=500，交叉概率Pc=0.9，变异概率Pm=0.01。

4.3 结果分析

通过使用遗传算法求得，总成本为201 016 469.62元。最终方案为：在节点3、6、9、12建立无水港。运输路线的分配关系如表7所示。

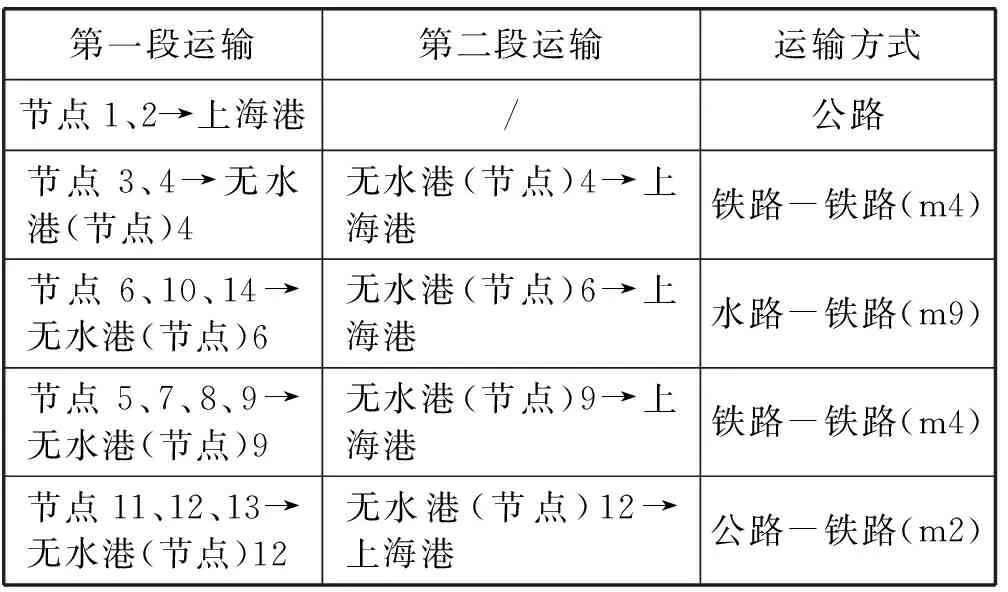
表7 运输路线分配及运输方式

如图5所示，最优解在接近300代时就已经趋于稳定。为了验证两阶段模型的有效性，跳过第一阶段，直接对24个城市进行无水港选址，求得最终的目标函数值为237 903 527.06元，而运算时间为12.24 s。通过将两阶段法获得的近似最优解和直接法获得的近似最优解相比，结果显示两阶段法的目标结果更优，且求解速度上有优势，证明了本文设计的两阶段模型是有效的。

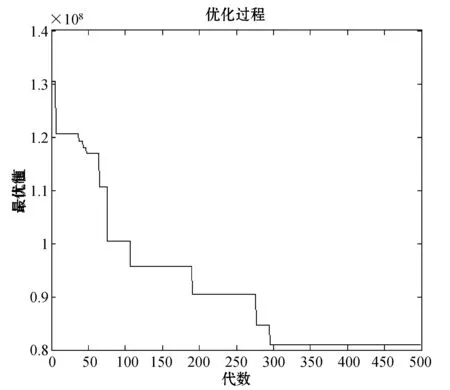
图5 遗传算法求解收敛图

表8显示，两阶段法得出的无水港建设成本、运输成本、换装成本各占总成本的24.4%、62.4%、13.2%。直接法得出的无水港建设成本、运输成本、换装成本各占总成本的27.9%、64.4%、7.7%。与直接法相比，本文建设成本下降了3.5%，运输成本下降了2%，换装成本提高了5.5%。对比结果表明，本文所用的方法更为经济。

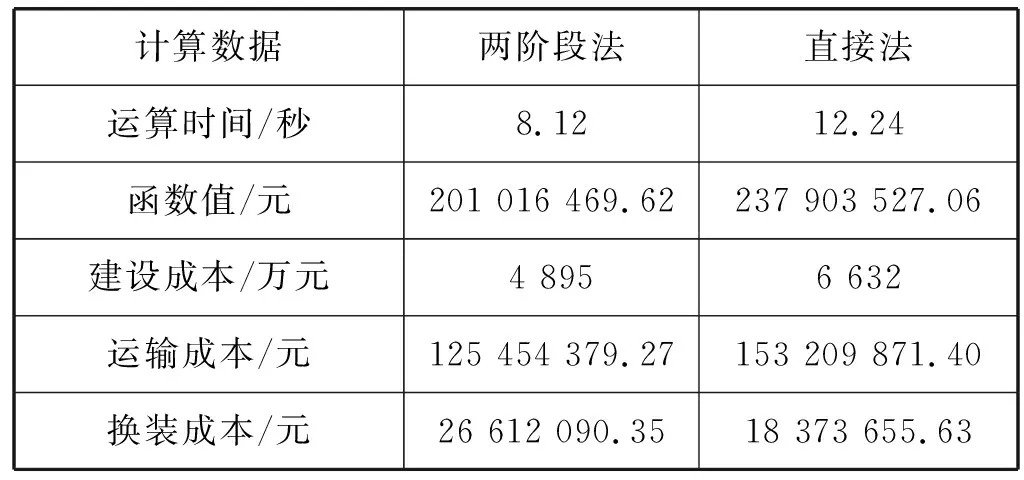
表8 两种方法对比

5 结 语

本文在“一带一路”背景下对无水港选址问题进行了研究，创新性地将无水港指标评价与选址优化方法结合运用，建立了两阶段模型的无水港选址模型，设计了模型求解算法解决问题。第一阶段建立指标评价体系筛选无水港选候选城市，第二阶段建立了包括运输成本、无水港建立成本、换装成本的目标函数，并利用遗传算法来确定无水港的选址问题。算例应用分析表明，本文构建的两阶段法通过逐步筛选和优化，满足了货源城市的运输需求，并且大大降低了总成本，与直接选址法相比，总成本降低了15.5%，验证了两阶段模型的有效性和合理性，以期为“一带一路”建设中的无水港选址研究提供理论参考和实践指导。