计及元件综合重要度和网络抗毁性的骨干网架搜索
2018-08-14杨为群黄辉郑春王淳于阳东
杨为群,黄辉,郑春,王淳,于阳东
(1.国网江西省电力公司经济技术研究院,南昌 330043; 2.南昌大学,南昌 330031;3.国网江西省电力公司,南昌 330077)
0 引 言
随着输电网的大规模和多区域互联建设,电网对大范围停电事故的抵御能力逐步增强。但自然界中存在不可避免的极端天气和自然灾害,这些均会对电力设施带来不同程度的破坏以及造成不可抵御的大面积停电事故,进而造成巨大的经济损失和恶劣的社会影响[1]。为了提高电网抵御停电事故能力以及有助于大停电后的供电恢复和重构,多采用在电网中构建骨干网架[2-4]。
现有骨干网架搜索方法主要是基本图论法和基于图论的人工智能方法。文献[5]在评估线路重要性的基础上,以基本图论法构建骨干网架。文献[6-8]则基于图论的人工智能方法搜索骨干网架,将元件重要性指标作为构成目标函数元素之一,但它们仅从结构方面评估元件重要度,没有考虑元件的其它属性。文献[9]利用成本效益法选择重要支路,构建骨干网架,其支路重要度评价指标是从骨干网架的功能出发进行构建,不能反应支路对整个网络的重要程度。文献[10]从网生存性角度出发提出了生存性综合指标,以构建相应骨干网架,但相关指标计算复杂且费时。文献[11]克服潮流在两节点之间只通过最短路径传输的假设,基于基尔霍夫定律提出电气介数,用于衡量支路重要性;文献[12]在文献[11]支路结构重要度的基础上,进一步考虑支路状态属性、社会属性,以综合衡量支路重要度。文献[13]从网络结构角度出发提出了基于节点邻居信息以及集聚系数的节点重要性评价指标,指标计算简单且能够有效反应节点在网络中的重要性。文献[14-15]提出一种整体衡量网络抗毁性的指标,为搜索骨干网架的目标函数的构建提供了一种新思路。
为了能够较为全面的评估电力系统中线路和节点的重要性,在传统电气介数的基础上,引进了表征发电机和负荷的社会属性的经济因子改进电气介数,用于衡量线路重要度;以线路重要性为权重,结合节点邻居信息以及集聚系数,构建了节点重要度指标。将线路重要度指标、节点重要度指标和网络抗毁性指标相结合,构建了考虑元件综合重要度和网络抗毁性的骨干网架数学模型,采用引导烟花算法[16]求解所建模型。
1 元件综合重要度和网络抗毁性评估
1.1 支路综合重要度
文献[12]考虑不同支路退运导致的相关经济损失不同,引入经济因子修正传统的电气介数,以表征元件的结构属性和社会属性。保证重要负荷的持续供电是骨干网架的主要功能之一,重要负荷所具有的社会属性更高,因此,采用经过经济因子修正的电气介数,用以刻画支路重要度,其计算如式(1)~式(3)所示。其中,式(1)是支路的重要度指标计算公式;式(2)、式(3)分别用于计算发电机节点和负荷节点的综合权重,不同于文献[12]的百分比求解方法,文中采用趋同化函数[13]进行求解,以正确反应两者作用的综合结果。
(1)
(2)
(3)
式中Iij(l)为在“发电-负荷”节点对(i,j)间加上单位注入电流元后在线路l上引起的电流,具体计算方法参见文献[11];Wi、Wj分别是考虑经济因子后发电机节点i和负荷节点j的综合权重;εi、εj分别是发电机节点i和负荷节点j的经济因子;ωi是发电机节点i的权重,取发电机的实际出力或额定值;ωj是负荷节点j的权重,取负荷实际值或峰值;NG、NL分别是系统发电机和负荷节点数。
1.2 节点综合重要度
考虑到节点在网络中的重要性不仅与自身信息相关,还与其相邻节点的信息有关,文献[13]提出了一种计算简单且有效的基于节点邻居信息及集聚系数的节点重要性评价指标。为了使该指标能够兼具电气性质,提出以支路重要度指标作为支路的权重来求解各节点的加权度,进而求取节点重要度指标,如式(4)~式(8)所示。其中,式(4)为节点重要度计算公式;式(5)为节点i加权度计算公式;式(6)为节点i与其邻居节点加权度之和计算公式;式(7)为节点i的集聚系数计算公式;式(8)为节点i的邻接节点间紧密程度计算公式。
(4)
(5)
(6)
(7)
(8)
式中DW(i)表示节点i的加权度;Ri表示节点i所连支路集;Γi表示节点i的邻居节点集合;NB为网络节点数;ei表示节点i与其任意两个邻居节点之间所形成的三角形的个数;ki为节点i相邻节点数。
求得支路和节点重要度指标后,利用式(9)对相应指标进行归一化,其中,Fmax为相应指标的最大值;Fmin为相应指标的最小值;Fi为第i个(条)节点(支路)的重要度指标。
(9)
利用式(9)处理后的元件重要度指标,其值越小,表示元件越重要。
1.3 网络抗毁性评估
元件重要度指标可用于辨识网络重要节点和关键线路,但不能够整体评价网络抗毁性。文献[14-15]提出了式(10)所示的网络抗毁性指标,用于衡量网络整体抗毁性能力。
(10)
式中λi、NC分别为网络所对应图的邻接矩阵的特征根以及特征根的数目;s为网络抗毁性指标,s值越大,表明网络抗毁性能力越好。
2 骨干网架搜索目标函数
骨干网架是一个包含规定的必须保障的重要电源节点、重要负荷节点、关键支路及其两端节点的、满足运行约束的电力网络。由于必须保留的元件一般不能构成一个满足约束条件的连通网络,为此,构建了以线路路数最小为目标,同时包含元件重要度指标和网络抗毁性指标的骨干网架搜索模型,具体如下:
(11)
式中xi表示支路i是否纳入骨干网架,xi=1表示纳入,xi=0表示不纳入;NL为网络支路数;B(i)表示支路i的重要度指标;P(j)表示节点j的重要度指标;Q表示骨干网架中支路端点集;s为骨干网架的网络抗毁性指标。
所对应的约束条件如下:
(1)潮流约束
潮流约束分为等式约束和不等式约束,即:
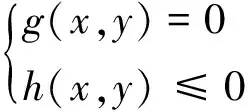
(12)
(2)连通性约束
所构造的骨干网架在包含所必须保留的节点和支路的基础上,保证连通,不存在孤岛。
3 基于引导烟花算法的骨干网架搜索
3.1 引导烟花算法
烟花算法(Fireworks Algorithm,FWA)作为一种新型的群智能优化算法于2010年提出,主要由爆炸算子、变异操作、映射规则和选择策略组成,由于其不弱于PSO的寻优效果得到广泛应用[17]。在爆炸算子中每个烟花都会产生诸多爆炸火花,在FWA算法中没有充分利用爆炸火花的相关信息。为了提高对爆炸火花所具有信息的利用程度,文献[16]引入引导向量(Guiding Vector,GV)和引导火花(Guiding Sparks,GS)用于改进FWA性能,构建了引导烟花算法(Guiding Fireworks Algorithm,GFWA)。GFWA的主要操作包括爆炸算子、映射规则和选择策略,在爆炸算子中根据爆炸火花求得对应烟花的GS。
GV是两组爆炸火花质心之间的差,两组爆炸火花分别是由相同个数的具有好的适应度函数值和具有不良适应度函数值的爆炸火花构成。GV能够为寻优提供良好的方向,同时其能够根据与最优点的距离自适应调整自身长度。
GS是将GV和与GV相对应的烟花叠加而获得,每一个烟花都有一个GS对应。GS提供了一种新的、简单的、设计合理且理论可靠和有效的方法来帮助进一步改进启发式算法中的信息利用,并且该理念可以容易地移植到大量基于群体的算法中。
(1)爆炸算子
作为烟花算法的核心部分,爆炸算子对烟花算法的性能起着至关重要的作用,主要包括确定爆炸强度、爆炸幅度。爆炸强度和爆炸幅度的计算原则是使适应度值更好的烟花在较小的范围内产生更多的火花,而适应度值较差的烟花在更大的范围内产生较少的火花。
将烟花分为两类:普通烟花和核心烟花(Core Firework,CF),核心烟花是当前烟花中适应度函数值最优的烟花,CF处于不断更新的状态,其爆炸幅度与上一代CF的爆炸幅度有关。相应公式如式(13)~式(15)所示,其中,式(13)用于确定烟花爆炸强度;式(14)用于确定烟花爆炸幅度;式(15)用于确定CF的爆炸幅度。
(13)
(14)
(15)
式中Si、Ai分别为烟花Xi的爆炸强度和爆炸幅度;Ymax为当前全体烟花中适应度值最差的个体的适应度值;f(Xi)为第i个烟花个体的适应度值;m、n分别为用于控制爆炸强度和爆炸幅度的常数;t为当前迭代次数;ACF(t)为第t代CF的爆炸幅度;ε为机器最小值,用于避免出现分母为零的情形;Cr、Ca分别为CF爆炸幅度的缩小和放大因子,这里分别取0.9和1.2。
确定烟花Xi的爆炸强度和爆炸幅度后,利用式(16)产生其第j个爆炸火花Ei(j)的第k维值:
Ei,k(j)=Xi,k+U(-1,1)·Ai
(16)
式中U(p,q)为区间[p,q]上一均匀分布随机数。
获得烟花Xi的爆炸火花后,按适应度函数值从优到劣排序后,利用式(17)和式(18)产生其对应的GV和GS:
(17)
SG(i)=Xi+VG(i)
(18)
式中σ用于确定每次获得GS时所需不同适应度函数值的爆炸火花数,其值事先给定。当乘积σSi不为整数时,采用向下取整的方式获得其整数值。
(2)映射规则
由爆炸算子产生的爆炸火花和GS中可能存在部分维度越限的情况,采用式(19)所示规则,将越限维度映射到可行域内。
Ei,k(j)=U(0,1)·(XUB,k-XLB,k)+XLB,k
(19)
式中XUB,k、XLB,k分别为第k维的上下限,其他同前式。
(3)选择策略
爆炸算子产生的爆炸火花、引导火花以及当前存在的烟花构成一个待选择群体,结合精英-随机选择策略,即适应度函数值最好的个体直接进入下一代,其他个体通过随机选择获得,以获得下一代个体,进行迭代运算。
3.2 基于GFWA的骨干网架搜索
以式(11)为目标函数,以支路为决策变量,应用GFWA搜索骨干网架,具体步骤如下:
(1)读入计算所需原始数据:网络参数和节点参数,初始化GFWA参数;
(2)根据原始数据和式(1)~式(3)计算支路综合重要度指标,根据计算得到的支路综合重要度指标,按式(4)~式(8)计算节点综合重要度指标,并按式(9)对相应指标进行归一化;
(3)初始化满足拓扑约束的烟花,将必须保留的元件所在维固化成1,计算各烟花的适应度函数值,确定核心烟花,并校验各烟花对应网架的潮流约束;
(4)对每个烟花进行爆炸操作,按式(13)~式(16)确定每个烟花对应的爆炸火花,计算各爆炸火花的适应度函数值,进行排序处理,然后按式(17)、式(18)确定每个烟花对应的引导火花;对于爆炸火花和引导火花中越限的维度按式(19)将其映射至可行域内;
(5)对由当前烟花、爆炸火花以及引导火花构成的群体,基于精英-随机选择策略,选择下一代烟花,更新核心烟花;
(6)判断当前迭代次数与最大迭代次数间的关系,若当前迭代次数小于最大迭代次数,则转至步骤(4);否则输出当前核心烟花,并转换为与其对应的核心骨干网架方案。
4 算例分析
以图1所示的IEEE-30节点系统为例,测试本文所提方法。采用MATLAB R2016b计算平台编制计算程序,运行环境为CPU型号Core i7-4790、主频3.60 GHz、内存16 GB的PC。系统包含41条支路和30个节点,在骨干网架中必须保留的重要支路是1-2和1-3,负荷节点中除节点16、18、23、26和29外均为必须保留的重要负荷节点,必须保留的发电机节点是节点5。GFWA的参数设置如下:烟花个数为1、爆炸强度控制常数m为50、爆炸幅度的控制常数n为1、σ为0.2,算法终止条件为目标函数计算次数达到 6 000。

图1 IEEE-30系统拓扑结构图Fig.1 Topology structure of IEEE-30 system
表1和表2中分别给出了归一化处理后的支路和节点重要度指标,表中“C”指考虑经济因子、“NC”指不考虑经济因子。
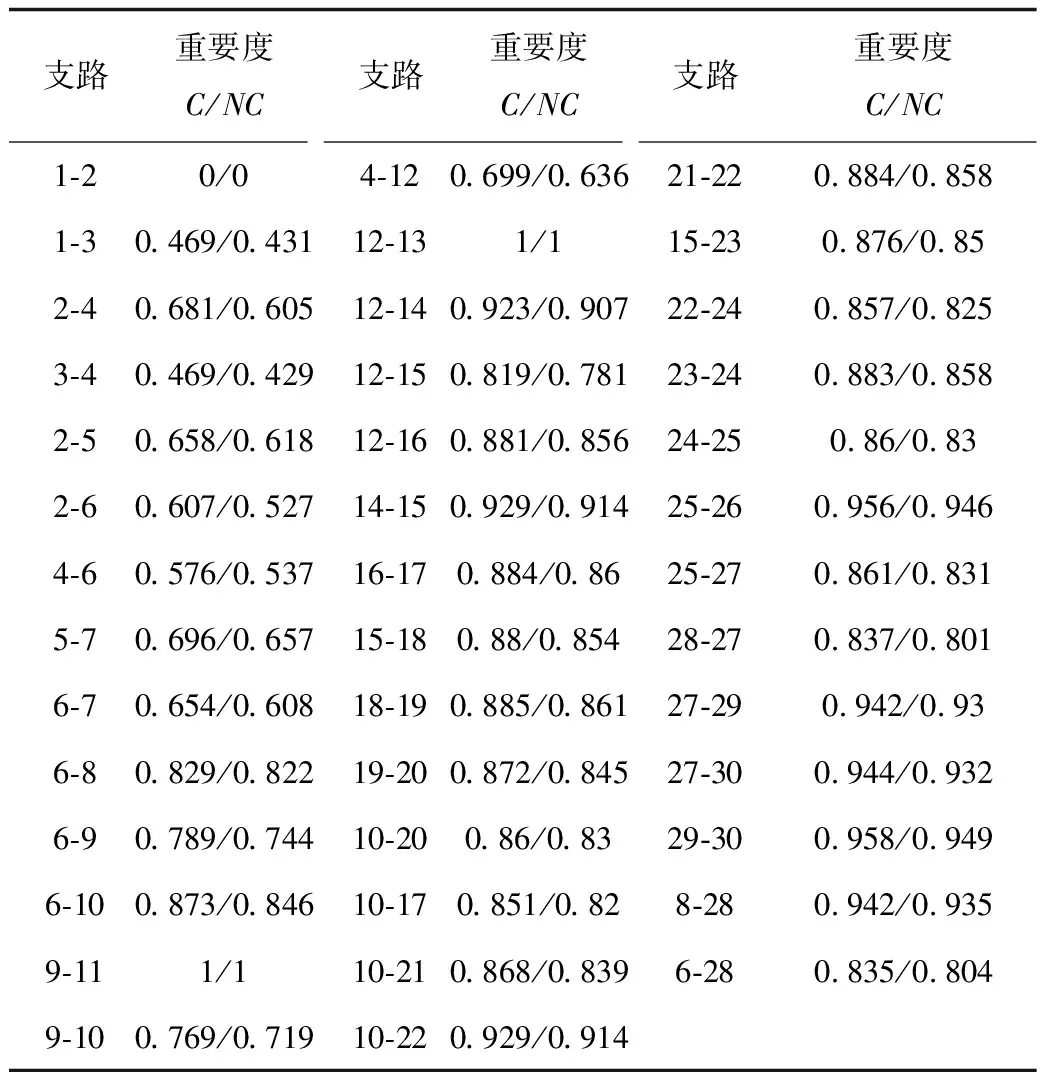
表1 不同情形下的支路重要度Tab.1 Branch importance index in different situations
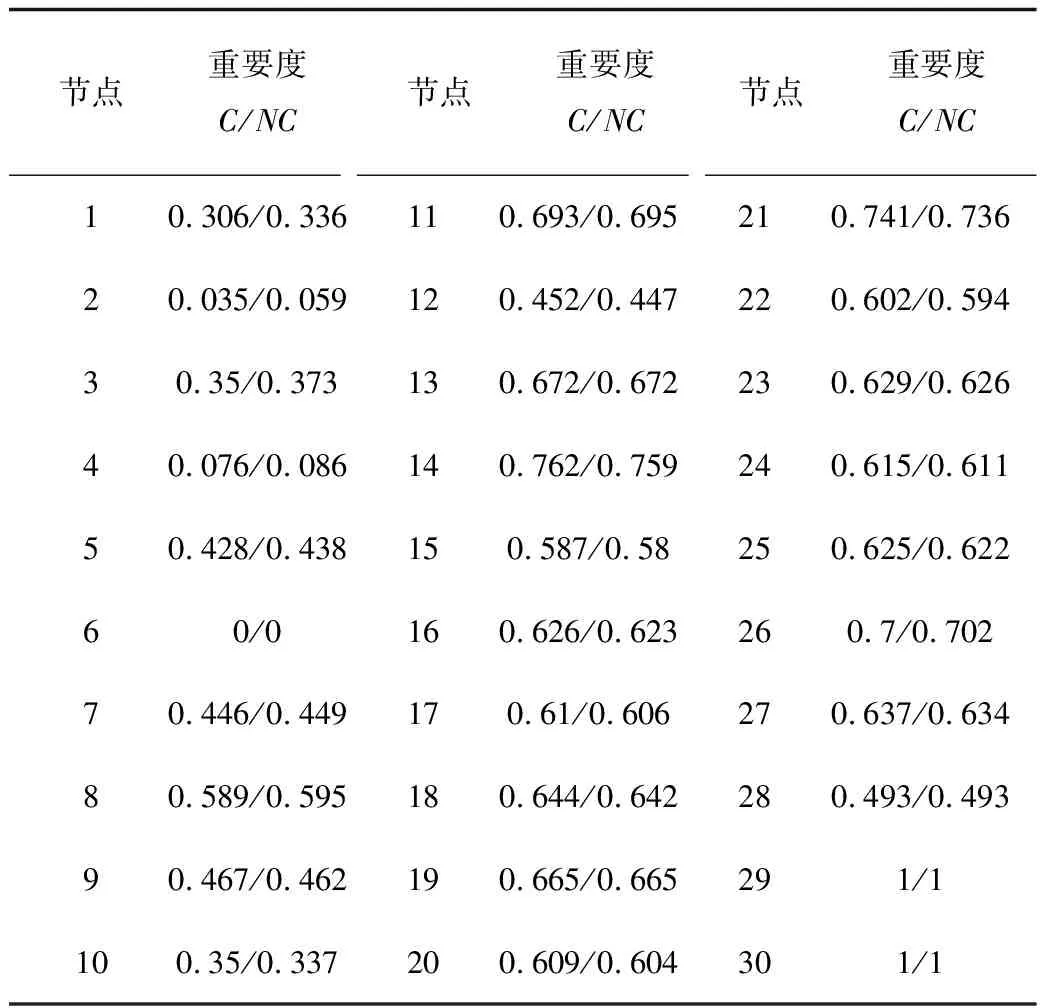
表2 不同情形下的节点重要度Tab.2 Node importance index in different situations
分析表1、表2可知,在元件重要度评估中纳入表征发电机或负荷停运损失的经济因子,使得评估指标同时包含元件的结构属性和社会属性,相比较仅考虑元件的结构属性,量值上有明显变化。
进一步分析表2可知,网络中节点的重要度程度不仅与其自身度(即邻接节点数)有关,亦与其邻接节点的度和节点间的支路权重有关:节点度值越大,其邻接节点间连接越紧密,节点重要度越大;相比于节点间的拓扑紧密程度,节点间的支路权重对节点重要度指标的影响更大。
利用GFWA算法,根据本文目标函数搜索得到了图2中实线表示的骨干网架。为对比分析,图3给出了不考虑网络抗毁性时搜索得到的骨干网架。二个图中实心点为必须保留的节点、空心点为搜索过程中得到的、用于确保连通性的节点。二个骨干网架均保留了20条支路、21个节点,二个图中所保留的节点一致,支路有5条不同;且二个图所示骨干网架在满足所保留负荷点用电需求的同时,最少化保留支路和节点,表明搜索得到的骨干网架是可行的。相对于图2,图3所得骨干网架中保留了较多的更为重要的支路,如支路3-4的重要程度要高于支路4-6;但图2所示的骨干网架的抗毁性(s=0.866 2)优于图3所示骨干网架(s=0.847 0),表明本文所构建目标函数搜索得到的骨干网架在纳入了重要的元件的同时,选择了具有更高网络抗毁性的拓扑结构,使骨干网架更为合理。
为了验证GFWA的性能,采用FWA对算例进行搜索以进行对比,FWA的参数设置与GFWA相同,两者的收敛曲线如图4所示。表3进一步给出了GFWA和FWA连续运行50次时,最优目标函数值的分布情况。
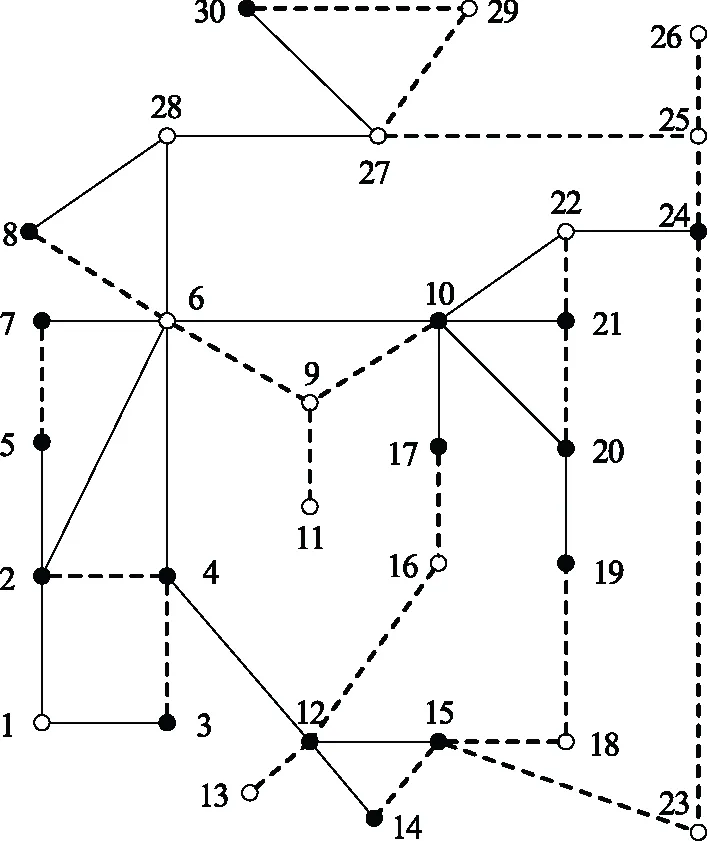
图2 计及网络抗毁性的IEEE-30系统骨干网架Fig.2 Backbone network of IEEE-30 system including network survivability
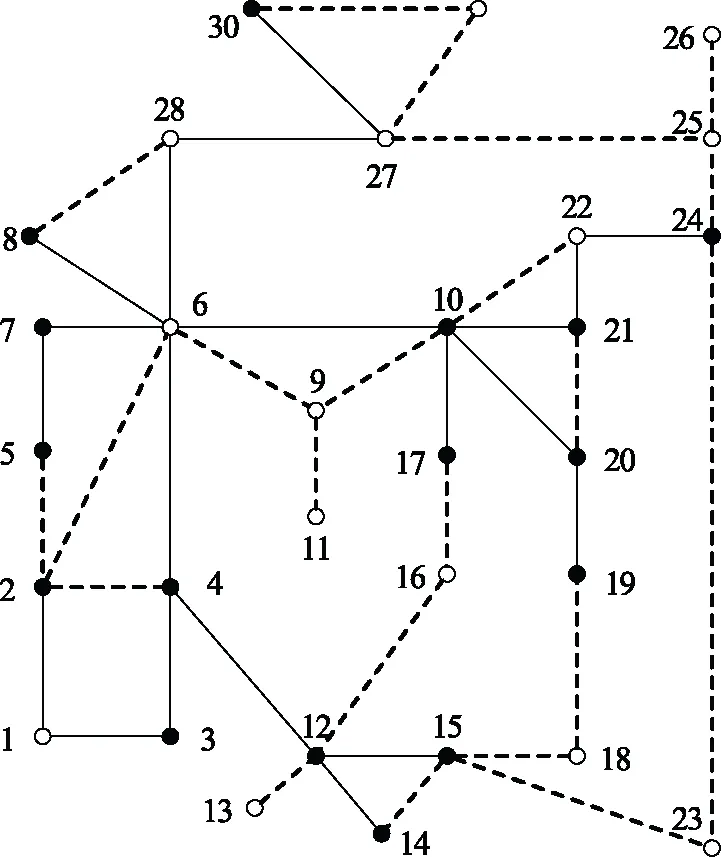
图3 不计及网络抗毁性的IEEE-30系统骨干网架Fig.3 Backbone network of IEEE-30 system excluding network survivability
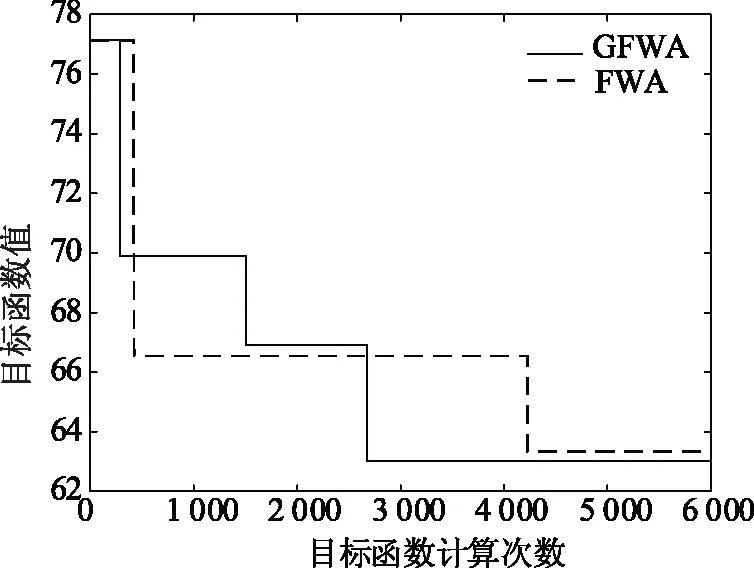
图4 GFWA与FWA收敛曲线Fig.4 Convergence curve of GFWA and FWA
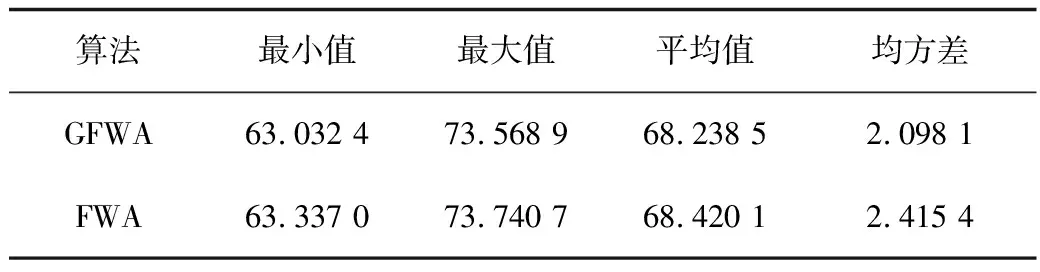
表3 GFWA与FWA的最优目标函数值分布Tab.3 Distribution of optimal objective function values of GFWA and FWA
分析图4和表3可知,相对于FWA算法,GFWA算法的迭代速度和最优个体质量均有明显提升。表明GFWA具有搜索能力强、收敛速度快、收敛精度高的特点。
5 结束语
在传统电气介数的基础上,引进了表征发电机和负荷的社会属性的经济因子改进电气介数,用于衡量线路重要度;将线路重要度作为边权重计算节点加权度,在考虑邻接节点间的紧密程度的基础上,基于加权度和集聚系数构建了计算简单、方便的节点重要度评估指标。
在考虑元件重要度的同时,引入网络抗毁性,构建了基于元件重要度和网络抗毁性的骨干网架搜索目标函数,以保证纳入重要程度高的元件的同时,使骨干网架具有较好的抗毁性。采用搜索能力强、收敛速度快、收敛精度高的GFWA算法搜索骨干网架。IEEE-30系统验证了所提方法的有效性。
