BCZT陶瓷的Nd3+掺杂机制与介电性能研究

丁士华，彭 勇，宋天秀，那文菊

(西华大学材料科学与工程学院， 四川 成都 610039)

具有ABO3型钙钛矿结构的无铅材料越来越受到人们的重视。特别是BaTiO3基铁电陶瓷，由于其优良的介电与压电性能，被广泛应用于陶瓷电容器及正温度系数电阻器等电子器件中[1-2]。掺杂的BaTiO3陶瓷，其居里温度高于室温(约120 ℃)，且介电常数较小，其使用性能受到限制。近年来，科研工作者对BaTiO3基陶瓷材料体系做了大量工作。在理论模拟方面，Lewis等[3]研究了在不同氧分压情况下各种本征和非本征缺陷能；Buscaglia[4]运用平均场模拟，发现杂质离子半径是衡量替代位置的一个重要参量。在实验方面，主要集中在BaTiO3基陶瓷体系的离子替位以及非化学计量比等方面，探索其结构与性能的关系[5-10]，研究表明：离子掺杂的替代位置、补偿机制都会对陶瓷电性能产生影响；离子半径及其化合价差异也将影响着材料的松弛行为[11]。由此可知：研究离子掺杂机制、介电松弛行为有助于改善BaTiO3基陶瓷材料的室温介电特性， 提高其使用性能。目前，通过实验与模拟相结合去描述其介电松弛行为，国内还鲜有报道。

对BaTiO3-BaZrO3陶瓷体的研究表明，Zr4+替代B位的Ti4+能离子可以使居里温度降低，介电峰值温度变宽[5-7]。Mitsui等[8]研究Ca2+添加到BaTiO3时发现，介电峰值发生微小变化，但峰值范围变宽。Baskaran等[9]也发现Ca2+的添加能微弱减小铁电相的转变温度。本课题组在研究Ca2+掺杂Ba(Ti0.82Zr0.18)O3时发现，Ca2+能减小陶瓷晶粒尺寸，且是很好的展宽剂，也可以调节居里温度[10]。为此，本实验以(Ba0.92Ca0.08)(Ti0.82Zr0.18)O3(简称BCZT)为基体材料。由于稀土元素在许多方面具有独特性质，因此常被用作添加剂。近年来，对BaTiO3体系陶瓷的掺杂改性备受关注。本文选用Nd3+对A位进行掺杂研究，讨论了(Ba0.92-xCa0.08Ndx)(Ti0.82Zr0.18)O3(简称BCZT-x，0≤x≤0.02)陶瓷样品的结构，模拟计算了各种缺陷能、缺陷簇能及溶解能，并对掺杂机制与介电性能做了分析和阐述。

1 实验过程与模拟方法

1.1 实验过程

以BaCO3、TiO2、ZrO2、CaCO3和Nd2O5为原料(分析纯)，采用固相反应工艺制备(Ba0.92-xCa0.08Ndx)(Ti0.82Zr0.18)O3(0≤x≤0.02)陶瓷样品。以去离子水为介质、二氧化锆球为磨介，机械球磨8 h，预烧温度为1 100℃，保温2.5 h。二次球磨后以质量分数8%聚乙烯醇水溶液作为黏结剂造粒，干压成型，圆瓷片的尺寸为Φ10 mm×1 mm，烧结温度为1 380℃，保温时间2.5 h，随炉冷却。烧结样品经磨光清洗后被银，用于介电性能测试。

利用X射线衍射(XRD)(DX-2500型)进行物相分析(管电压35 kV，管电流20 mA，X射线源为CuKα1，λ=1.54056Å，其中扫描速度为2°/min，扫描范围2θ为20～80°)；样品的介电性能采用LCR阻抗仪(Agilent4284型)进行测试，测试频率范围为1 kHz～1 MHz，测试温度范围为-30～130℃。

1.2 模拟方法

近些年，分子动力学模拟方法被广泛应用于材料科学领域，特别是钙钛矿结构氧化物的缺陷形成研究广泛采用原子尺度的模拟计算。本文采用分子动力学模拟(GULP)软件[12]计算BaTiO3基陶瓷中缺陷的能量。该软件是基于Born的晶体离子模型，运用Mott-Littleton方法模拟晶格缺陷的形成能量，离子之间的作用势采用经验公式和Dick和Overhauser的壳模型

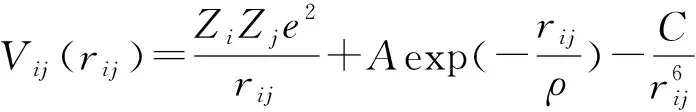
(1)

α=q2/k，

(2)

去计算材料中本征和非本征缺陷能量。式(1)中第1项为库仑作用势， 第2项为Buckingham排斥势，第3项为Van der Waals 势。式(2)壳模型描述了离子的极化效应。式中：Zi、Zj为离子电荷；e为电子电荷；A、ρ和C分别是buckingham的势参数；rij为相互作用离子的间距；α为极化系数；q为壳层(shell)电量；k为核(core)与壳层的弹性系数。式(1)和(2)计算中采用的势参数如表1所示。

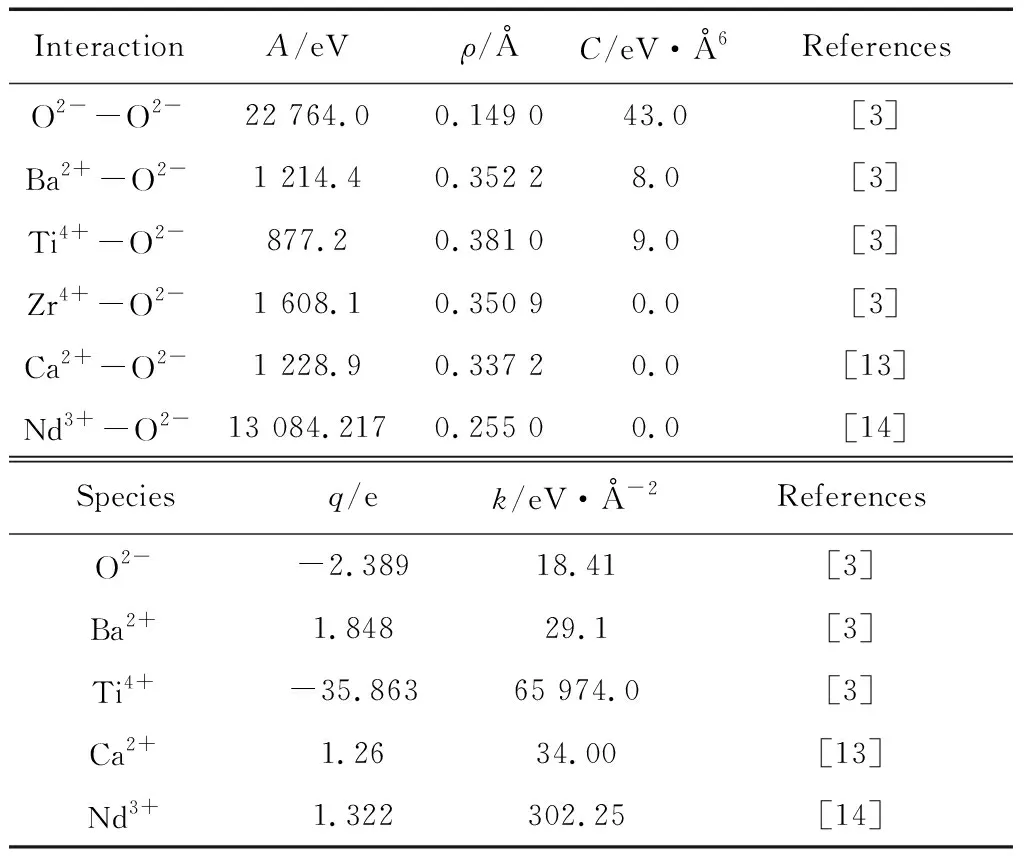
表1 Nd3+掺杂BCZT陶瓷的势参数

2 结果与分析

2.1 XRD分析

图1为掺杂不同量Nd2O3的BCZT陶瓷样品的XRD图谱。由图可知：当x≤0.01时，各组分样品均为单一的四方钙钛矿结构，当x≥0.015时，出现第二相，表明Nd2O3在BCZT陶瓷的固溶度小于0.015。

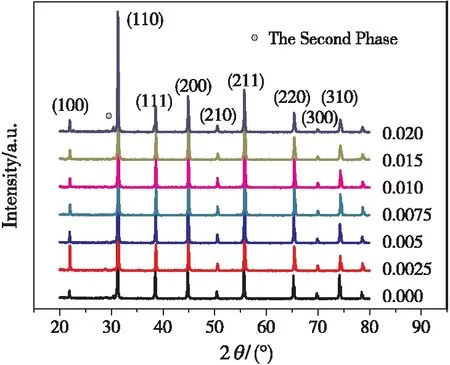
图1 不同掺杂量BCZT陶瓷样品的XRD图

2.2 掺杂机制分析

为了研究Nd3+掺杂BCZT陶瓷Ba位的各种补偿机制，采用缺陷化学的方法对Nd3+：BCZT晶体存在的缺陷模型进行讨论，缺陷方程用Kroger-Vink符号表示。

① Nd3+替代Ba2+产生传导电子平衡

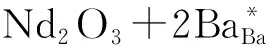
(3)

(4)

② Nd3+替代Ba2+产生Ti4+空位平衡

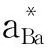
(5)

(6)

③ Nd3+替代Ba2+产生Ba2+空位平衡

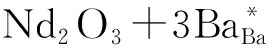
(7)

(8)

④ 电荷自我补偿

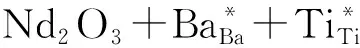
(9)

(10)

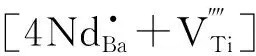
Ebinding-energy=Edefect-associate-∑Eisolated-defect

(11)

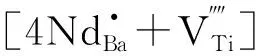
表2 Nd3+掺杂BCZT陶瓷的替代能和溶解能

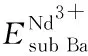
表3 用于计算Nd3+掺杂BCZT陶瓷溶解能的一些表征能量

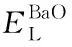
Tsur等[15-16]在研究稀土离子掺杂BaTiO3陶瓷的占位情况时发现：当杂质离子半径大于0.094 nm(6配位)时，优先进入A位。同时，Takada等[17]研究表明，当Ti4+过量时，Nd3+也会优先进入Ba2+位。 因此，当Nd2O3掺杂BCZT陶瓷时，Nd3+(0.0983 nm/6配位)优先固溶到A位。这与模拟计算Nd3+替代Ba位的能量比Ti位低是一致的(见表2)。不等价替代产生的缺陷补偿机制由A、B位元素摩尔比率(n(A)/n(B) )决定[16]。

一方面，通过表2溶解能可知，优先补偿方式为传导电子补偿，而事实上，大量研究表明，三价稀土离子只有在极少量施主掺杂下才可能发生电子补偿，如谢道华等[18]发现只有Nd3+掺杂量x≤0.002时，BaTiO3陶瓷才会发生电子补偿。同时，Shaikh等[19]在研究Nd2O3(0.01≤x≤0.05)掺杂BaTiO3时发现介电损耗较低，认为掺杂不是由电子补偿完成，并且发现Nd3+替代Ba位，电荷补偿由Ti空位来完成。 在本文Nd3+：BCZT(x≥0.002 5)陶瓷中，由样品较低的介电损耗，如图3所示，可知，当x≥0.002 5时，掺杂补偿机制不是由传导电子完成。

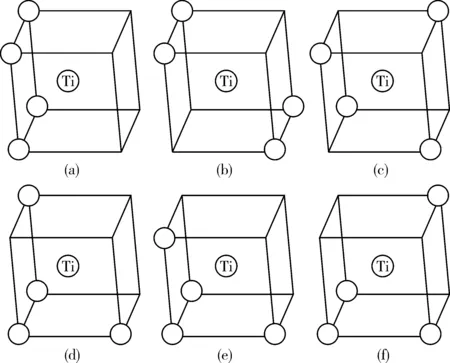
图缺陷簇的微观结构模型

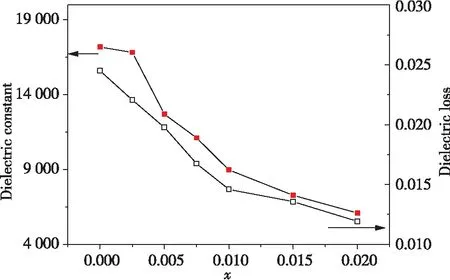
图3 1 kHz下BCZT-x陶瓷样品介电性能与掺杂量的关系

另一方面，表2也表明自我补偿机制的溶解能也较低。Hirose等[20]实验证实，在n(Ba)/n(Ti)=1时，发生自我补偿，且固溶度随烧结温度的增加而增加，在1 300℃时，固溶度达到0.12。Buscaglia等[4]在模拟计算杂质离子掺杂BaTiO3陶瓷的补偿机制时也发现，Er3+(0.089 nm)、Y3+(0.090 nm)、Tb3+(0.092 nm)、Gd3+(0.094 nm)掺杂时，缺陷补偿机制更偏向于自我补偿。这与当0.087 nm≤r≤0.094 nm, 此类离子被看作两性离子，既可发生受体掺杂也可发生授体掺杂是一致的[15-16]。Nd3+半径为0.098 3 nm，接近两性离子范畴，并且Nd3+(0.0983 nm)几乎在Ba2+(0.135 nm)和Ti4+(0.0605 nm)的中点，故可知：在BCZT-x陶瓷中，自我补偿机制可能发生；但由于补偿机制与n(A)/n(B)的比率密切相关，本文n(Ba+Ca)/n(Ti+Zr)<1，所以补偿机制④，即自我补偿不会占主导地位。结合溶解能的计算，在本研究材料体系中，随着Nd3+浓度增加，补偿机制②优先发生。

2.3 介电性能分析

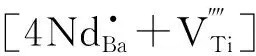
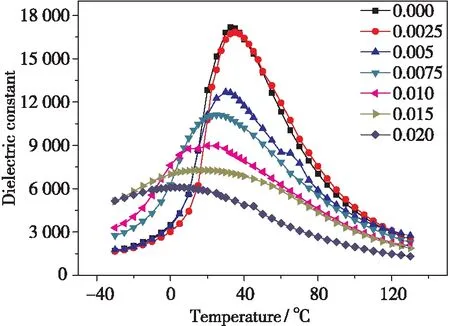
图4 1kHz下BCZT-x陶瓷介电常数与温度的关系

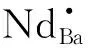
不同频率下BCZT-x陶瓷样品的介电常数与温度的关系如图5所示。

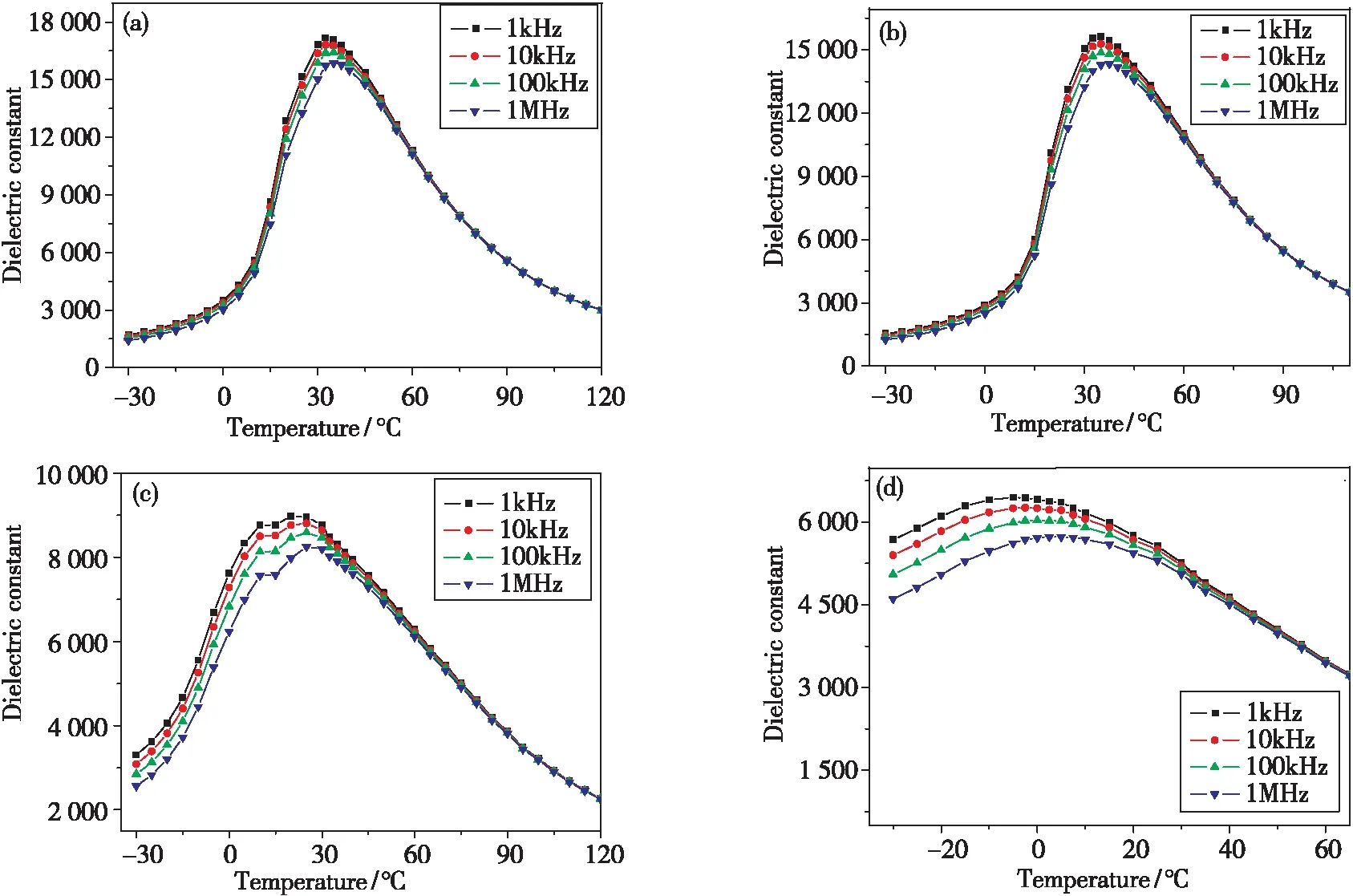
图5 x=0.000(a)、0.0025(b)、0.010(c)和0.020(d)下BCZT-x陶瓷样品介电温谱图

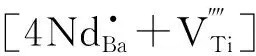
3 结论

1)Nd3+掺杂BCZT陶瓷后，主晶相为四方BaTiO3结构，当x≥0.015时，出现第二相。随着Nd3+掺杂量增加，介电常数和介电损耗均减小，介电峰值温度向低温移动。

2)结合实验，通过GULP模拟可知：在BCZT-x(x≥0.0025)陶瓷中，随着Nd3+浓度增加，Ti4+空位补偿机制优先发生，可能会伴随少量自我补偿。

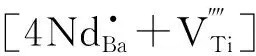
特约作者介绍

丁士华(1963—)，男，安徽怀宁人，1981.9—1988.6在西安交通大学电子工程系学习， 获电子科学与技术(电子材料与元件)学士、硕士学位，2004年获同济大学材料学博士学位。国家自然科学基金委评审专家、科技部项目评审专家、上海市科委项目评审专家、教育部学位论文评审专家。

主持、参与完成国家级、省部级等各类科研项目20余项。在国内外学术刊物上发表学术论文140余篇，被SCI/EI/ISTP收录文章70余篇。担任Journal of the American Ceramic Society、IEEE Transactions on Industrial Electronics、IEEE Transactions on Dielectrics and Electrical Insulation、Journal of Materials Physics and Chemistry 等多家国内外学术刊物审稿人。