力传感器模型辨识及动态补偿器设计*

王镜森 曹家勇 姚淳哲 吴玉春

(上海应用技术大学机械工程学院，上海 201418)

近年来，随着我国制造业的飞快发展，自动化生产线与智能制造技术不断完善，对力检测系统的动态特性的要求也随之不断提高。力传感器作为力检测系统的最前端，如果动态性能不能达到使用要求，也就不能快速、无失真地反应随时间变化的动态力信号，使力检测系统拥有较大的动态误差。例如在机床检测与故障诊断过程切削检测的应用场合，切削力变化频率快、成分复杂，检测精度要求高。需要在现有传感器基础上，利用数字化动态补偿技术，有效改善检测系统的频响特性。在这种背景下，对力传感器进行动态补偿是改善力传感器动态特性的一条有效途径。动态补偿常用的方法包括零极点配置法、系统辨识法、神经网络算法等[1-8]。其中零极点配置法原理简单，较易实现。

建立准确可靠的传感器模型对研究传感器动态特性至关重要。目前国内外对建立传感器数学模型的研究已经比较成熟，常用的模型辨识方法主要有两种[9]：一种是根据传感器的结构特性与工作原理推导出传感器系统的数学模型；另一种方法是通过实验采集传感器输入输出的数据并进行系统辨识建模。文献[10]介绍了一种传统的即通过手工描点法绘图，然后手工量取相关量进行计算的方法。这种分析方法显然工作量巨大，而且计算精度差，所得模型误差较大。文献[11]提出一种最优化建模方法，使传感器系统在误差允许的范围内简化为较简单的模型，这种方法计算量较小，且所求得的模型更简单。文献[12]研究了最小二乘法在系统辨识中的应用，将沃尔什函数应用于最小二乘法参数辨识中。文献[13]提出了一种改进的具有更快收敛速度和和更强鲁棒性的FLANN，该网络成功用于压力传感器动态建模。文献[14-15]使用神经网络辨识的方法，建立了传感器的辨识模型，通过跟踪补偿环节的变化可以获得传感器特性的各种变化。

1 力传感器模型辨识

为了获取力传感器的动态性能指标(阻尼比，固有频率)，需要对其进行动态建模。建立传感器数学模型有两种方法：一种解析法，是使用各种物理定律以及系统的结构数据推导出模型；另一种方法是利用实验数据辨识出系统模型，称为系统辨识法。

1.1 系统辨识法

系统辨识的具体过程是指通过对传感器采集其输入和输出数据并进行动态标定，使用系统辨识的方法获取传感器一定形式的数学模型。系统辨识的特点是把传感器系统看成一个黑箱，仅仅依据实验数据建模。这种方法能够充分获取传感器的动态特性并且简单易行。通过系统辨识获得的模型并不直接反映出传感器的结构特性和工作原理。由于这种方法无须深入了解传感器的结构特性与工作机理，因此系统辨识方法非常具有实用性。系统辨识法中应用最小二乘法辨识模型参数的研究已经相当完善，被广泛应用。

1.2 非线性最小二乘法估计参数

设使用一非线性函数f(c,x)对已知一组实验数据(xi,yi)(i=1,2,…,m)进行拟合，其中c=(c0,c1,…,cn)为待拟合系数。首先给拟合系数一个初始值，并记为cj(0)(j=1,2,…,m),且使

cj=cj(0)+δcj

(1)

如果能够确定δcj，则可确定cj的值。为求出δcj，将拟合函数f(c,x)在cj(0)附近作泰勒级数展开，并略去δcj的高次项，当x=xi时有

(2)

式(2)中，

f0(c,xi)=f(c0(0),c1(0),…,cn(0),xi)

(3)

(4)

如果可以确定待拟合函数的函数形式，并已知实验数据xi时，选定合适的cj(0)，可求出式(3)及式(4)，这样函数f(c,x)就可以简化看作一个关于变量δcj的线性函数。

可根据最小二乘法定义函数f(c,x)拟合残差的平方和为：

I=∑[f(c,xi)-yi]2

(5)

将(2)代入式(5)得：

(6)

由式(6)可知，I是关于δcj的函数。当∂I/∂δcj=0时，可以确定δcj的值，即

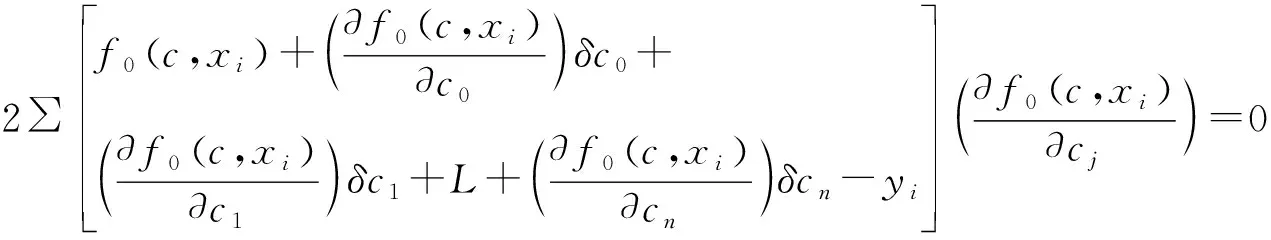
(7)

整理式(7)得法方程：

A×C=B

(8)

在式(8)中：

(9)

B=(b0,b1,b2,L,bn)T

(10)

C=(δc0,δc1,δc2,L,δcn)

(11)

在矩阵A中，

在列向量B中，

在已知数据(xi,yi)和cj(0)后，就能够通过解法方程求出δcj的值。

当求得的|δcj|比较大时，可以通过式(1)进行迭代计算，直到|δcj|可以忽略为止，从而得到最终的cj值,得到辨识模型。

2 动态补偿环节设计

2.1 动态补偿原理

动态补偿的实质就是在传感器原有的系统特性下串联一个动态补偿滤波器，拓宽原传感器系统通频带，使瞬态信号的全部或主要频率分量不被改变。在补偿设计时，由于存在测量噪声，这就导致补偿后高频信号的放大引起噪声的放大，噪声会严重污染测量信号，甚至使得补偿失去意义。对此，可以在满足测量要求的前提下考虑添加非理想补偿环节。动态特性补偿原理如图1所示。

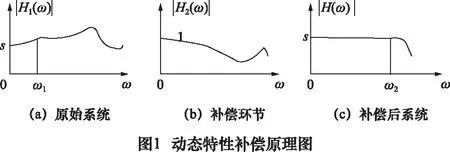
图1a中的截止频率ω1通过添加图1b补偿环节将其截止频率拓宽到图1c中的ω2，传感器系统的工作频带变宽，能够通过系统的频率分量变多，可以更好复现原输入信号的动态特性。

2.2 零极点配置法设计补偿环节

传感器系统的动态性能指标与传感器系统的传递函数零极点位置有密切联系。通过在传感器后串接一个补偿环节，可以将原传递函数不符合要求的极点相消除，重新调整新加入的极点位置，使传感器的动态特性满足实际使用要求。零极点配置法设计动态补偿环节简单易行，且补偿效果好。零极点配置法设计动态补偿环节的实现可以是各种各样的。

假设传感器为二阶系统时，其离散传递函数为

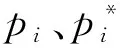
响应的动态补偿器为

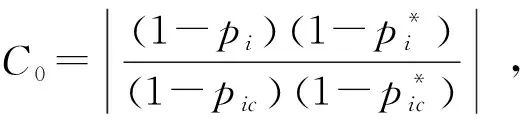
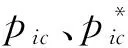
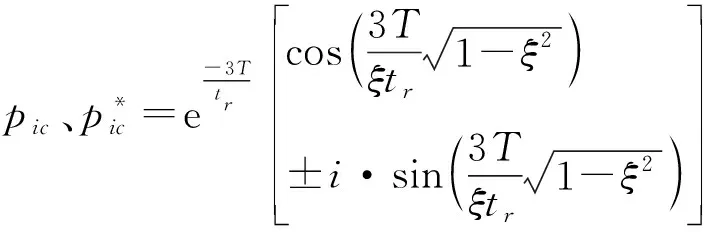
由于在零极点配置法设计动态补偿环节过程中，需要依据传感器的传递函数对零极点进行分析。因此，要求传感器模型精度较高，但并不严格。零极点配置法适用于响应曲线上升时间长、调节时间长且超调量大等动态特性较差的传感器系统。

3 实验验证与系统实现

现选择如图2所示一双弯曲梁力传感器进行实验,采集数据。具体实验装置组成包括力传感器、信号放大器、数据采集卡和数据处理软件。其中力传感器选择常用的双弯曲梁力传感器，信号放大器放大倍数为1 000倍，数据采集卡选择同步高速数据采集卡(USB_ HRF4626)，数据采集软件界面如图3所示，数据处理软件选择Matlab实现。

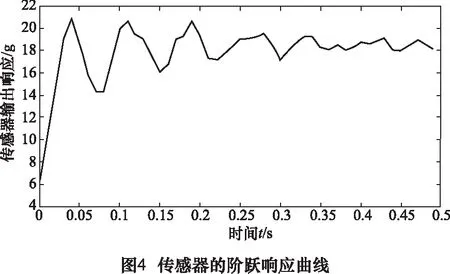
使用该实验装置进行传感器的阶跃响应实验数据采集，采集频率为1 000 Hz。并对该传感器进行静态标定，得到该力传感器的阶跃响应曲线如图4所示。

3.1 力传感器模型辨识

针对图4所示阶跃响应曲线进行非线性拟合，得到该传感器的辨识模型为

其中：ξ=0.188 3，ωn=85.821 5。

得到的阶跃响应曲线如图5所示，通过比较拟合前后的曲线可以看出拟合后的曲线较好地体现出了传感器的阶跃响应动态特性。

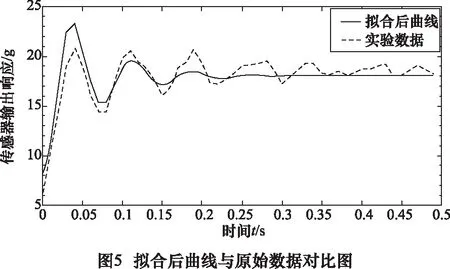
3.2 动态补偿环节仿真设计与效果

根据所得该传感器辨识模型做出单位阶跃信号下的力传感器归一化输出曲线如图6中可以看出该传感器的动态特性较差，上升时间tr=0.02 s，峰值时间tp=0.04 s，调节时间ts=0.2 s，超调量σ≈58%。

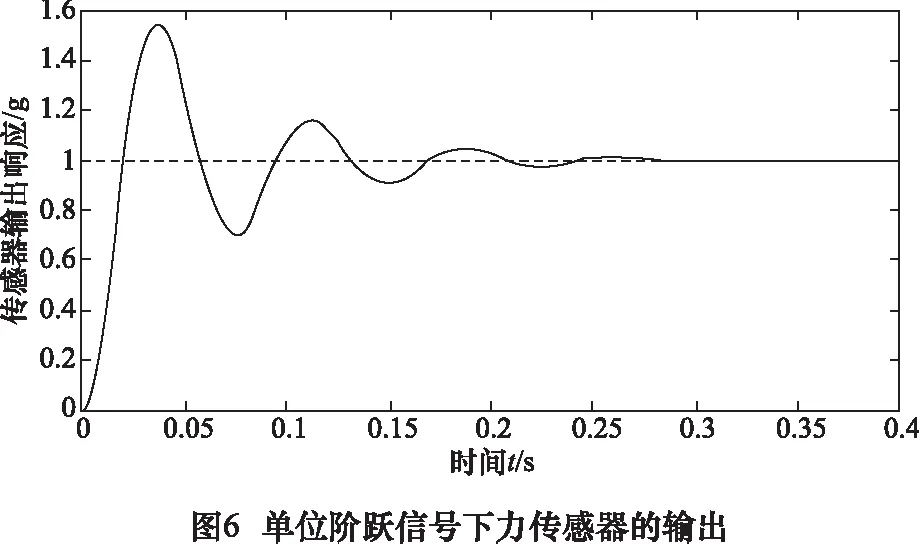
根据零极点配置法设计动态补偿滤波器来对传感器进行动态补偿。设计的补偿环节为

在传感器后添加该补偿环节，通过Matlab仿真得到补偿后的单位阶跃响应输出曲线，如图7所示。补偿后上升时间tr=0.008 s，峰值时间tp=0.01 s，调节时间ts=0.05 s，超调量σ≈4%。

从表1可以看出该传感器通过添加补偿环节后其动态特性有显著提高。

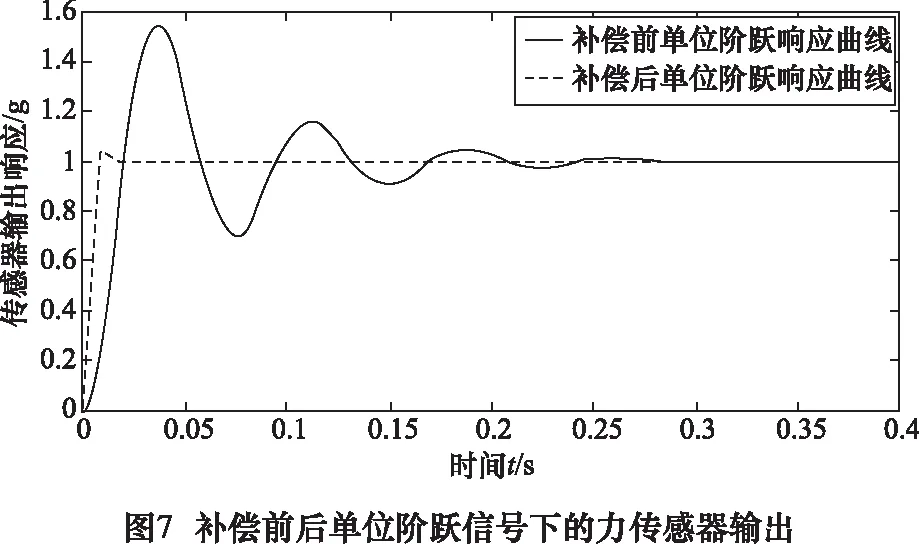
表1 补偿前后单位阶跃信号下动态特性比较

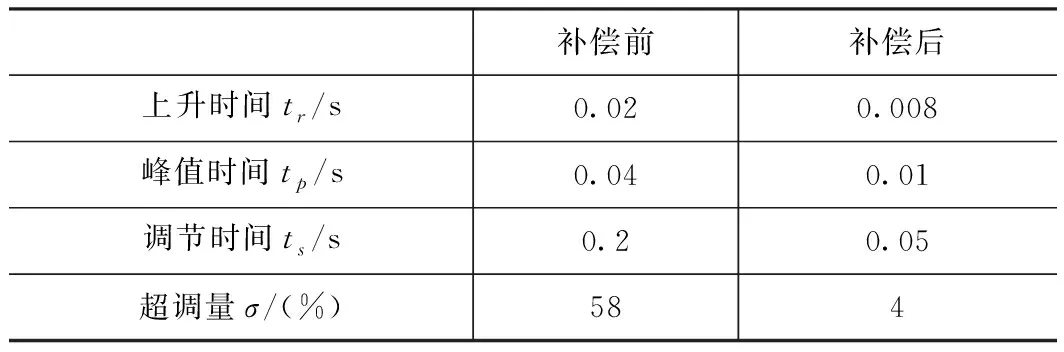
补偿前补偿后上升时间tr/s0.020.008峰值时间tp/s0.040.01调节时间ts/s0.20.05超调量σ/(%) 584

3.3 动态补偿环节实验设计

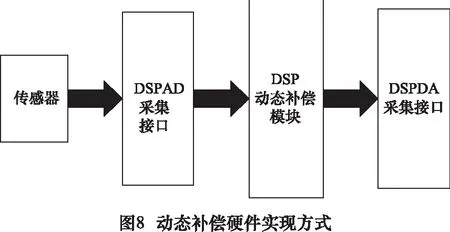
通过之前介绍的零极点配置法可以得到动态补偿环节的离散传递函数。当被测信号不需要实时处理的情况下，可以采用软件补偿的方法实现动态补偿器的设计，所有的数据处理在信号采集结束后由软件进行，这样可以节约额外的硬件成本，而动态补偿环节也可以灵活设计。当被测信号需要实时处理使用时，就必须采用数值算法来实现动态补偿数字滤波器的设计。数字滤波器的硬件设计可以使用数字信号处理器(简称DSP)来实现，采用这种方法可以获得较快的数据处理速度，实现复杂的数字信号处理运算。具体实现方式如图8所示。当传感器对力检测后产生信号经DSP的AD采集接口传送到DSP中，经DSP编程设计动态补偿模块完成传感器的动态补偿环节，补偿后的被测信号经DSP的DA采集接口传出以实现实时处理的要求。

4 结语

本文针对力传感器的动态特性进行了分析，研究了传感器的系统建模和动态补偿的问题。

根据力传感器动态特性难以满足实际要求，利用非线性最小二乘法比较切合实际地建立了传感器的辨识模型，研究了零极点配置法设计了传感器的动态补偿环节的方法。最后通过实验验证了最小二乘法在建立非线性系统模型的可行性，并且证明了零极点配置法所设计的补偿环节可以满足对传感器的使用要求，可以将该补偿方法应用于工程实际当中。