一种自紧厚壁圆筒非线性混合硬化模型及残余应力分析

符史仲， 杨国来

(南京理工大学 机械工程学院， 江苏 南京 210094)

0 引言

火炮身管是一种典型厚壁圆筒结构，通过自紧工艺，不仅能提高身管强度和寿命，还能减轻身管质量、提高火炮的机动性能。在自紧加工过程中，对残余应力的计算准确与否将直接影响到自紧身管弹性承载能力及疲劳强度等的设计计算，因此建立一种能准确描述身管材料机械特性的本构关系模型至关重要。

炮钢是身管的主要材料之一，具有以下材料性能：1)正向加载时应力变化较小，近似线弹塑性模型；2)卸载时的弹性模量略低于加载时的弹性模量；3)反向屈服应力小于正向屈服应力，具有明显的包辛格效应；4)反向加载时应力、应变具有明显的非线性关系。为了描述炮钢的上述特性，许多学者提出了相应的材料模型。李开平[1]以有限元模拟液压自紧身管，建立各向异性混合硬化模型，考虑屈服面的平移、缩放和旋转，残余应力计算值与试验值吻合较好，但该模型的材料参数较难通过试验获取。韩锦章[2]引入包辛格效应曲线，提出了基于Prager模型的非线性混合硬化模型，建立自紧厚壁圆筒模型，发现计算值与试验值吻合，而由于包辛格效应曲线需多次进行不同预应变下的拉压试验，获取困难。颜勇等[3]基于Mroz多屈服面模型，建立4段线性模型用于近似描述炮钢的本构关系模型，分析了自紧厚壁圆筒残余应力分布情况，计算值与试验值吻合，但多屈服面模型建模复杂，材料参数多。马新谋等[4]推导双线性随动硬化数学模型，将加载、卸载时的应力线性化，描述机械自紧过程的应力、应变变化，厚壁圆筒残余应力计算值与试验值较为吻合，然而未考虑的应力、应变非线性关系易引起误差。曾志银等[5]基于Johnson-Cook模型建立了炮钢的动态本构模型，并采用高斯- 牛顿迭代法优化材料参数，该本构模型验证试验采用了Taylor杆试验系统，试样长度- 试样半径与试验值最大误差不超过5%，但未对包辛格效应进行研究。

由于能模拟材料的平均应力松弛和棘轮效应，文献[6]提出的非线性随动硬化(AF)模型得到广泛应用，且该模型能反映炮钢的材料特性，可用于身管的有限元模拟中。Chun等[7]基于AF模型和各向异性屈服准则并增加背应力反向加载项，建立了各向异性非线性随动(ANK)硬化模型，为验证模型准确性，进行了拉伸仿真，将ANK模型、Chaboche模型、Geng-Wagoner模型等计算得到的应力与应变曲线与试验数据作比较，结果表明ANK模型更符合试验结果。Kobayashi等[8]建立了循环黏塑性混合硬化模型，针对临界面的特征引入了基于背应力的分次径向返回算法，又提出了适合混合硬化模型的新形式一致切线刚度矩阵，并通过缺口棒循环拉伸仿真验证了该模型的正确性。谢昌吉[9]建立了超细晶材料的混合硬化模型，以Al-Mg合金验证了该模型在不同单调拉伸和不同循环拉压加载工况下的应力与应变曲线和试验数据吻合。余海燕等[10]基于Barlat屈服准则建立了混合硬化模型，用U形件的回弹仿真验证模型正确性，该模型计算值、各向同性硬化仿真结果均与试验数据进行对比，前者回弹量更接近试验值。

相对于上述模型，自紧身管的残余应力分布受包辛格效应的影响较大，且不同的预应变下会出现不同程度的包辛格效应[11]，因此在本构关系模型中必须予以考虑。本文建立了一种基于AF模型的非线性混合硬化模型，能描述应力、应变间的非线性关系以及随塑性变形增大而减小的屈服面演变规律。硬化模型将背应力分解成若干项，每个子项的背应力均服从AF模型演化规律，还包含了用于描述包辛格效应的非线性各向同性硬化模型。再结合参量间的本构关系推导出张量形式的一致切线刚度矩阵，以用于整体有限元方程组的迭代求解和提高计算收敛速度。为获得模型的材料参数，以拉伸试验结果为优化目标，通过遗传算法得到最终的材料参数。以该组参数为基础建立自紧厚壁圆筒的有限元模型，分析残余应力分布情况，通过与双线性硬化模型和试验数据的对比，验证炮钢本构模型的准确性。

1 适用于自紧身管的非线性混合硬化模型

针对自紧身管的材料特性，利用有限元软件Abaqus提供的接口模块，开发了一种可适用于自紧身管的非线性混合硬化模型。该模型包含了服从AF硬化模型的背应力项和反映屈服面缩放的非线性各向同性硬化项。根据所建立的本构关系模型，提出了相应的本构积分算法。为提高整体计算的收敛速度，结合所建立的本构关系模型和各参量间的弹塑性关系，推导张量形式的一致切线刚度矩阵。

1.1 非线性混合硬化模型

非线性混合硬化模型包含屈服准则、流动准则和硬化准则。

屈服准则采用von Mises屈服函数，流动准则为关联流动准则，二者即为基于von Mises准则的J2流动理论[12]，利用了应力张量的偏量部分。

硬化准则有背应力硬化准则和屈服面硬化准则。背应力演化方程基于AF模型，即

(1)

(2)

卸载时，应力状态有移入屈服面的趋势[12]，这时有

(3)

式中：f为屈服函数；σij为应力张量；Dijkl为弹性刚度张量。以(3)式判断应力的加、卸载状态。

1.2 隐式积分算法

由于1.1节所建立的本构方程中存在大量的微分方程，需要在数值计算时对这些微分方程进行求解。为保证计算的稳定性和精确度，本节采用隐式积分算法求解本构方程，并用于后续的程序编写。

假设第n步为当前增量步，各个变量值都已算出，并给定第n+1步的应变增量张量Δεij，则可通过积分算法求解出满足本构方程的应力张量σij. 以下变量用下标n表示第n步的值，用下标n+1表示第n+1步的值。

(4)

(5)

1.3 张量形式的一致切线刚度矩阵

为将材料的弹塑性本构关系模型引入有限元分析，不仅需要计算每个积分点的应力状态，还需要提供与材料的弹塑性本构关系及其积分算法密切相关的一致切线刚度矩阵，供这一增量步的整体方程组平衡的迭代求解[14]。本文将应力方程微分，利用硬化模量、屈服函数及其他弹塑性方程，推导出一致切线刚度矩阵。该矩阵虽为非对称张量，但仍可利用对称张量的矩阵形式方便地编写成程序，且不存在逆矩阵的求解，从而避免了6×6矩阵的复杂求逆过程，降低了编程难度，减少了计算时间。

由关联流动准则可知，塑性因子λ的大小与应力增量张量dσij在屈服面外法线上的投影呈正比，即

(6)

式中：H′为硬化模量。进而根据流动准则，得

(7)

对屈服函数取微分，并联合(1)式和(7)式，得

(8)

式中：f为von Mises屈服函数。消去(8)式中的公共项(∂f/∂σmn)dσmn，并联合屈服函数，解(8)式得

(9)

由应力与应变关系和(7)式，可得

(10)

解(6)式、(9)式和(10)式得

(11)

为方便之后的方程推导，根据塑性流动方向nij，可设如下张量：

(12)

(13)

(14)

(15)

(16)

式中：G为剪切模量。对(13)式进行微分，有

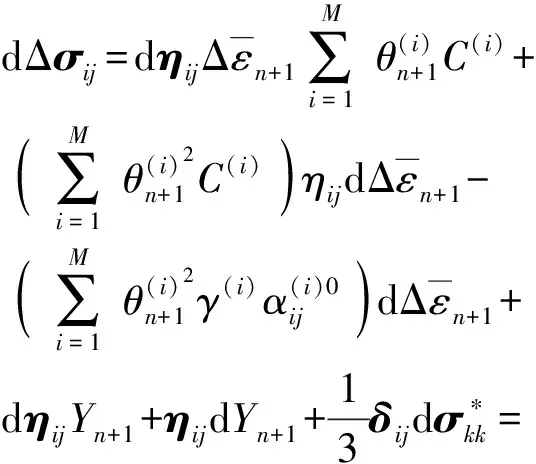
(17)

故(17)式可化简为

(18)

1.4 一致切线刚度矩阵的验证

表1 牛顿迭代法计算的收敛情况

2 材料参数选定

目前常采用的材料参数确定方法有两类：一类是试验法，进行如拉伸、压缩、剪切或循环等试验，以获取应力与应变曲线，然后通过拟合该曲线获得材料本构参数；另一类是参数优化方法，该方法以材料参数为优化变量，以试验结果为优化目标，通过优化方法调整变量并调用有限元软件进行计算，直至计算值与试验值一致。这类方法充分利用了有限元仿真与试验的优点，以简单、技术成熟的试验代替高难度的技术、不成熟的试验，具有易实现、方便应用的特点[10]。对于本文建立的本构模型参数，弹性模量、泊松比、初始屈服应力等参数，可通过简单拉伸试验绘制的应力与应变曲线获得；而其他材料参数，即(1)式和(2)式中的C(i)、γ(i)、Q∞、b，由于难以从试验中获取，故需要通过优化方法获得。

参数优化的目的在于寻找一组合适的材料参数，使得计算结果与试验结果间的误差最小，即满足以下目标函数：

(19)

为了高效快速地寻找最优解，本文采用遗传算法，并结合Isight和Abaqus两种软件，用以得到最优的材料参数。相比于传统优化算法，遗传算法不需要导数等解析性质信息，且具有全局寻优能力，比较适应于高维、多峰、求解不连续、具有凹凸性的问题。优化流程框图如图2所示。

根据以上方法得到了非线性混合硬化模型的材料本构参数C(i)、γ(i)、Q∞、b的优化值，如表2所示。

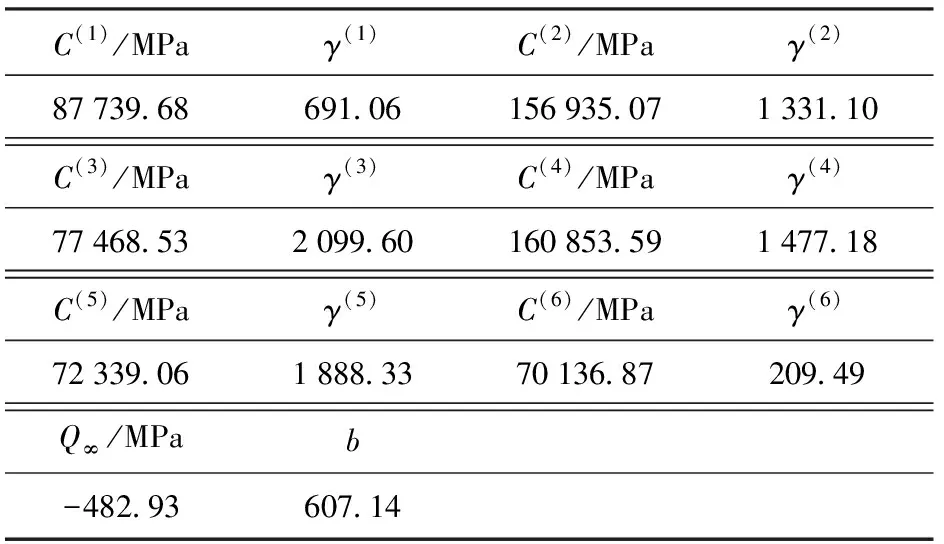
表2 参数优化值

3 自紧厚壁圆筒残余应力有限元分析

自紧工艺主要有液压自紧、挤扩自紧和爆炸自紧，其中液压自紧是在身管内壁充满高压液体，身管从内到外产生塑性或弹性变形。卸压后根据原有的应力状态，壁内形成塑性和弹性区域，产生相应的残余应力。

3.1 有限元模型

模型采用内径12.515 mm、外径26.200 mm的光滑厚壁圆筒，内壁承受均匀内压788.4 MPa. 其材料参数为拉伸弹性模量E=206.0 GPa，卸载弹性模量E′=198.0 GPa，泊松比ν=0.27，拉伸屈服应力σ0=935.4 MPa.

本文通过Abaqus/Standard程序建立厚壁圆筒的有限元模型，并应用子程序UMAT建立炮钢的本构模型，通过设置*Depvar和*User Material将状态变量和材料参数输入至Abaqus软件中进行迭代求解。

3.2 数值计算结果及分析

数值计算得到的切向、径向残余应力与双线性混合硬化(BLH，即正反向加载时的应力与应变关系简化为线性)模型得到的结果如图3所示。

试验结果数据源于文献[1]，该试验采用膛削法测量厚壁圆筒在不同半径处(共17处)的残余应力，其中厚壁圆筒的尺寸参数与本文算例一致。由图3可以看出，在内壁处的切向应力，本模型计算结果与试验结果相吻合，在其他应力区的计算结果与试验数据间的误差较小，基本吻合。在内壁处，BLH模型的计算结果偏大，在其他应力区的计算结果与试验结果相差较大。

4 结论

为了描述自紧身管的残余应力分布情况，本文建立了一种基于AF模型的非线性混合硬化模型，并以拉伸圆棒和厚壁圆筒有限元模型为算例进行验证。

1)建立非线性混合硬化模型。硬化模型包含若干背应力子项，每个子项的背应力均服从AF模型演化规律；还包含了用于描述包辛格效应的非线性各向同性硬化模型。通过本构模型间的关系，推导了张量形式的一致切线刚度矩阵，并模拟简单拉伸试验验证了该矩阵的正确性和有效性。

2)计算残余应力分布情况。以简单拉伸试验结果为优化目标，通过模型参数优化验证并确认了炮钢的本构模型参数。由厚壁圆筒的数值计算结果可知，本文建立的本构关系模型能较准确地反映残余应力的分布情况。

由于目前该模型仅考虑了准静态条件下的力学特性，而高温动态条件下(如火炮发射)材料的许多性能都会发生改变，发生诸如高温蠕变、屈服应力增大等现象，这需要更进一步地完善本构关系模型。