船舶典型节点弯曲载荷作用下极限强度试验研究
2018-08-14王晓强胡耀愚严仁军
王晓强 ,胡耀愚 ,严仁军
1海军驻中国舰船研究设计中心军事代表室,湖北武汉430064
2高性能舰船技术教育部重点实验室,湖北武汉430063
3武汉理工大学交通学院,湖北武汉430063
0 引 言
船舶结构包含的构件种类繁多,各种构件相互交叉连接形成节点,节点处通常有肘板加强结构,所有的构件都通过节点连接在一起组建成船舶整体。因此,连接节点的力学性能会直接影响到船舶结构的承载能力[1-2]。
Jordan等[3]于1978年统计分析了50艘各类船舶的12种结构节点,总计490 230个节点,包含破坏节点3 307处。其中,因产生裂纹发生破坏的有2 227处,这2 227处中有1 135处破坏是发生在肘板节点连接处,占总破坏数的50.97%。1980年,Jordan等[4]再次统计分析了 36艘船舶的117 374处节点,其中破坏节点 3 555处,而这3 555处中又有2 637处破坏发生在肘板节点上,占总破坏数的74.2%。
Lim等[5-6]利用有限元研究了肘板对接框架接头处节点的应力分布和极限强度,并根据节点的力学特性重新设计了肘板形状,有效改善了结构的应力。王波等[7]在ANSYS中建立梁连接节点的壳单元模型,对几种常见的船舶节点进行了屈曲强度性能计算,研究了肘板尺寸变化对节点承载力的影响。邓乐等[8]通过有限元计算,对梁肘板节点进行了一系列研究,讨论了肘板厚度、骨材端部间隙以及肘板臂长对节点强度和应力分布的影响。李伦[9]提出了一种新的用于内部平面舱壁的肘板节点结构形式,并对这种新型节点结构形式进行了全面的优化研究,改善了肘板的应力集中现象。史战新[10]对某水下结构物的肘板节点结构进行了疲劳寿命仿真研究,其研究对象包括三角形节点和圆弧形节点,得出圆弧形节点寿命比三角形节点寿命高56.8%的结论。李骥[11]基于ANSYS设计语言APDL,对矩形肘板的节点结构进行拓扑优化,并与三角形节点和圆弧形节点进行对比,分析了它们在应力集中和重量方面的优劣性。刘甜甜[12]采用OPTISTRUCT软件对肘板节点结构进行形状和拓扑优化,得到了节点材料的最佳分布,极大地降低了节点区域的应力集中。
目前,对船舶节点强度的研究主要集中在利用有限元软件进行结构优化方面,而有关船舶节点的试验研究还十分缺乏。本文将以典型的2种船舶节点——三角形肘板加强节点和圆弧形过渡加强节点(以下分别简称为“三角形节点”和“圆弧形节点”)为研究对象,设计大、小2组试验试件,每组包含1个三角形节点试件和2个圆弧形节点试件,对每个试件进行弯矩载荷下的极限强度试验,并对比分析它们的载荷位移曲线、极限承载力以及破坏位置与现象,用于为船舶的节点优化设计提供参考。
1 试验模型
试验中的2组试件尺寸根据实际某船舶甲板横梁与横舱壁竖桁以及连接节点尺寸,结合试验条件进行设计,每组试件包括1个三角形节点试件和2个不同圆弧大小的圆弧形节点试件。
1.1 试件尺寸
如图1所示,试验试件包括横梁和竖桁以及连接两者的节点,将图中6个试验试件(单位:mm)分别进行编号:A1,A2,A3;B1,B2,B3。其中试件A1为三角形节点试件,三角形节点腹板的尺寸为8 mm×350 mm×350 mm,试件A2和A3为圆弧形节点试件,其圆弧半径分别为650,550 mm。试件B1为三角形节点试件,三角形节点腹板的尺寸为5 mm×250 mm×250 mm,试件A2和A3为圆弧形节点试件,其圆弧半径分别为450,350 mm。
1.2 测点布置
为考察试验过程中试件节点以及横梁竖桁上的应变变化,在每个试件上均布置了21个测点,分别布置在节点上腹板局部应力较大点和其对应面板中间,以及横梁和竖桁上局部应力较大点与应力梯度较大的位置。面板上和应力梯度较大位置处的主应力方向明确,故测点位置采用单向应变片测量;横梁和竖桁相接处以及节点腹板上的应力复杂,故测点位置采用三向应变片测量。具体位置如图2所示。
试验中,用WBD百分表测量位移,每个试件有2个位移测点,如图3所示。同组试件的位移测点相同,1号测点位于横梁加载点下方,2号测点位于横梁中部下方。
2 试验设计
2.1 试验工装
结合试验平台的条件,根据试验的约束和加载要求,设计试验工装如图4所示,其通过反力架和千斤顶提供集中载荷,千斤顶下放置力传感器,由力传感器控制和记录集中载荷的力的大小。整个试件固定在地基滑道上,同时竖桁上部的夹具限制其在弯曲方向的位移,以保证在试验过程中弯曲载荷全部作用在节点处。
2.2 试验过程
在进行极限强度试验之前,对试件进行多次加载和卸载,以释放试件的加工残余应力。试件共承受2个载荷:第1个是竖桁上的固定载荷,由实际甲板承受的压力转换而来;第2个是横梁上的弯曲载荷,由横梁端部的千斤顶集中加载产生,是试验的主要驱动力,由它的大小来测定各试件的极限承载能力。
试验加载分2步。对于A组的3个试件,首先加载竖桁上的载荷至10 kN,然后以8 kN分级加载横梁上的弯曲载荷,每加载一级,待试件稳定后再采集所有的应变以及位移数据,直至极限载荷。到达极限载荷后,随着千斤顶的加载,载荷反倒会逐渐下降,最后缓慢加载至试件破坏。B组试件的加载流程与A组相似,竖桁上的载荷为3 kN,以4 kN分级加载弯曲载荷并采集数据,直至极限载荷,然后缓慢加载至试件破坏。
3 结果分析
试验中,竖桁上的载荷较小,加载后,试件应力场的变化极小,故本节主要分析横梁上的弯曲载荷对试件的影响(本节中出现的“载荷”均指弯曲载荷),并将竖桁上载荷加载后的状态作为弯曲载荷的零点。
3.1 载荷—位移曲线
如图5(a)所示,根据A组试件的载荷—位移曲线,可知A1,A2和A3这3个试件在极限载荷前的刚度变化可以分为3个部分:加载前期刚度不稳定部分、加载中期刚度稳定部分和加载中后期刚度逐渐下降部分。其中,加载前期刚度不稳定是因为试件与工装间不可避免地产生了间隙;随着载荷的增加,间隙消除,加载中期的载荷和位移呈良好的线性关系;到加载至接近极限载荷时,曲线斜率减小,试件的刚度逐渐减小,直至极限载荷时刚度为0。继续加载,载荷随着位移的增加反而减小,产生了负刚度。3个试件中,刚度最大的是试件A2,其次是试件A1,试件A3的刚度最小。由图5(b)可知,B组3个试件的载荷位移变化与A组相似,试件B2的刚度略大于试件B1,试件B3的刚度最小。将各试件在极限承载力之前的载荷位移值进行最小二乘法线性拟合,拟合的直线斜率即为各试件极限载荷前的平均刚度,具体如表1所示。

表1 试件刚度Table 1 Stiffness of specimens
结构的极限承载力是指结构完全崩溃前所能承受外荷载的最大能力。在载荷—位移曲线中,曲线最高点对应的载荷即为试件的极限承载力,也就是试件承载弯曲载荷的极限强度。由图5可知,试件A1,A2和A3的极限承载力分别为305,264和208 kN,试件B1,B2和B3的极限承载力分别为145,102和95.5 kN,其中试件A1的极限承载力比试件A2的大15.5%,比试件A3的大46.6%;试件B1的极限承载力比试件B2的大42.2%,比试件B3的大51.8%。通过分析2组试件的极限承载力,可以看出,三角形节点试件的极限承载力比圆弧形节点试件的大,这是因为三角形节点形成了局部框架,提高了试件的承载能力。
将各组试件的极限承载力和极限承载力前的平均刚度进行无因次化,则极限承载力为:A1∶A2∶A3=1.16∶1∶0.79,B1∶B2∶B3=1.42∶1∶0.93;极限承载力前的平均刚度为:A1∶A2∶A3=1∶1.21∶0.79,B1∶B2∶B3=1∶1.07∶0.76。B组 3个试件间极限承载力的变化比A组3个试件的剧烈;A组3个试件间极限承载力前的平均刚度变化比B组3个试件的剧烈,两组试件间的差异可能是由尺度效应所引起。
3.2 应力应变分析
为验证应变数据的有效性,从所有试件的应变数据中随机提取了60个测点的应变数据,并对每个测点加载初期的前10个数据进行了应变—载荷线性拟合,拟合结果的相关系数如图6所示。由图可见,在60个随机测点中,大部分测点线性拟合的相关系数都大于0.98,而小于0.98的测点相关系数仍大于0.8,可见本次试验应变数据在加载初期具有很好的线性度,测量结果真实有效。
由测点布置可知,每个试件节点的软趾处都布置了三向应变片,当A组试件的弯曲载荷F=48 kN时,试件A1,A2和A3节点软趾处的最大主应力分别为-193.24,-151.70和-161.92 MPa;当 B组试件的弯曲载荷F=24 kN时,试件B1,B2和B3节点软趾处的最大主应力分别为-229.18,-200.16和-182.34 MPa。在同等载荷条件下,试件A1节点软趾处的最大主应力比试件A2的大27.4%,比试件A3的大19.34%;试件B1节点软趾处的最大主应力比试件B2的大14.5%,比试件B3的大25.7%。
3.3 破坏位置与现象
试件A1的破坏位置位于横梁面板和腹板上与三角形肘板相接处。开始加载后,与三角形肘板相接处的横梁腹板首先屈曲并向一边凸起,随着横梁腹板凸起程度的变大,与三角形肘板相接处的横梁面板也屈曲并向另外一边折皱,最后试件破坏,破坏时,三角形肘板没有明显变形,如图 7(a)所示。
试件A2的破坏位置位于横梁面板圆弧段和直线段过渡区域。开始加载后,过渡区域的横梁腹板首先屈曲并向一边凸起,随着横梁腹板屈曲程度的变大,此处的横梁面板也屈曲并向另外一边凸起,如图7(b)所示。
试件A3的破坏位置位于横梁圆弧节点与竖桁相接区域。开始加载后,横梁腹板首先屈曲并向一边凸起,随着横梁腹板屈曲程度的变大,角点处焊缝和腹板产生了撕裂,如图7(c)所示。
A组3个试件的破坏位置和变形程度各不相同,分析原因如下:
1)试件A1的三角形肘板形成了框架,整个三角形框架的刚度很大,直到三角形肘板破坏也未产生明显的变形。这相当于在横梁面板和三角形肘板相接处给横梁提供了一个刚性支点,弯矩载荷大部分被横梁承受,且此处横梁腹板上产生了应力集中,导致此处横梁腹板首先屈曲变形并带动面板变形,随着载荷的增加,横梁上腹板产生屈曲的面积和程度增大,最后整个试件达到极限承载状态,当载荷继续增加时,变形增大但承载力反而会减小。
2)试件A2的大圆弧腹板过渡减轻了横梁腹板上的应力集中,整个横梁圆弧段上的应力比较平均。圆弧段和横梁直线段过渡区域的应力集中最大,当载荷增加时,此处首先屈曲变形并带动面板变形,随着屈曲的面积和程度的增大,整个试件达到极限承载状态。
3)试件A3的小圆弧腹板在与竖桁相接处形成了很小的尖角,导致此处应力集中非常严重,随着载荷的增加,此处横梁腹板屈曲变形剧烈,当到达极限承载状态时,由于变形太大,横梁腹板与角点焊缝产生了撕裂裂纹。
试件B1,B2和B3的破坏位置及破坏现象与试件A1,A2和A3相似,如图8所示。由此可见,节点的形式决定了试件的破坏形式,而试件大小对破坏形式没有影响。
4 有限元分析
使用有限元软件ABAQUS,按照试验中各试件的具体尺寸建立6个试件的三维有限元模型,计算其极限承载能力。以试件A1为例,其整体模型如图9所示。
模型单元采用S4R单元,S4R单元为四节点曲壳单元,适用于薄壳或厚壳结构建模。有限元模型的长度单位为mm,力的单位为kN。有限元模型的约束条件和载荷条件与试验一致,即在底部支座处固定3个方向的位移和转角,竖桁顶部约束平行于横梁方向的线位移,在试件加载处施加位移载荷。经网格收敛性分析,有限元模型采用的网格大小为20 mm。
有限元模型的极限承载力计算结果如表2所示,与试验实测值相比,计算值与试验值之间的相对误差在±6%以内。
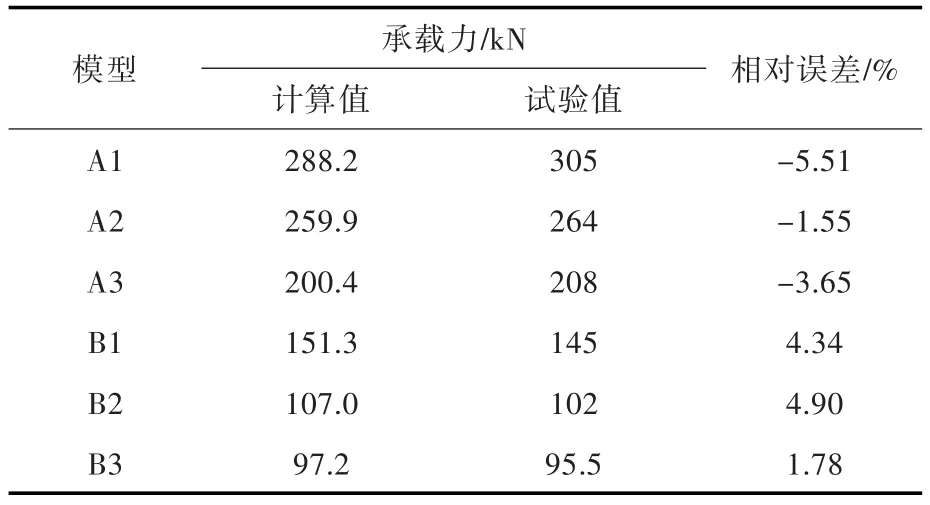
表2 有限元计算的极限承载力与试验值的对比Table 2 Comparison of ultimate strength between finite element models and experiments
图10所示为有限元模型的破坏模式(以A组试件为例)。由图可见其破坏位置和现象与试验结果基本一致,这说明有限元计算模型能够很好地模拟试验的过程和结果,验证了试验结果的正确性。
5 结 论
本文对三角形节点以及大、小圆弧形节点的极限强度性能进行了2组试验研究,并进行了对比,同时,还通过有限元计算验证了试验结果的正确性,主要结论如下:
1)比较试验中同组3个试件的节点,当采用三角形肘板连接时,可以在节点处形成局部框架,相对于圆弧连接,其对局部有加强作用,所以其极限承载力大。同时,由于三角形肘板在软趾处形成了应力集中,软趾处的主应力比圆弧形过渡节点软趾处的大,因此在同等外载荷条件下,相比于三角形肘板连接,圆弧过渡的连接方式可以降低节点处的峰值应力。
2)不同大小、相同节点形式的试件破坏形式相同,而大小相同、节点形式不同的试件破坏形式差别很大,说明节点形式决定了试件破坏形式,而试件大小基本不影响试件破坏形式。
3)通过将2组试件的试验数据无因次化后进行对比,发现2组试件3个试件间的极限承载力与极限载荷前平均刚度的变化规律相同,但变化的程度不同,2组试件间的差异可能是由尺度效应所引起。有关尺度效应对极限承载力和刚度的具体影响和作用还有待进一步的研究。
4)有限元计算可以很好地模拟试验的结果和现象,可以用于船舶节点设计的模拟分析,简化节点的设计过程,并为船舶节点的强度优化提供指导。
