基于梁弯曲理论的飞机结构件腹板刚性评价模型*

龚清洪 牟文平 骆金威

(成都飞机工业(集团)有限责任公司，四川 成都 610092)

随着航空领域快速发展，对飞机性能需求不断提高，薄壁整体结构件被广泛应用于新一代飞机设计中。航空整体结构件日趋复杂，具有大量薄壁和腹板等弱刚性结构，并且加工精度要求越来越高，导致制造难度越来越大。在加工过程中经常发生由于局部刚性过差引起的工件超差、报废，大幅增加制造成本。结构件刚性是装夹设计、工艺方案设计和切削参数选择时需要考虑的重要因素。在加工前对工件刚性进行科学评价，是优化加工方案和切削参数的前提条件，在飞机结构件生产制造过程中的作用日益突出。目前关于薄壁工件刚性评价的研究主要采用两种方法，第一种是采用有限元仿真分析研究工件变形，进而评价工件刚性；第二种是利用优化算法建立装夹-工件-加工变形之间的关系来评价工件刚性。

在有限元仿真研究方面，袁俊凇[1]仿真分析了汽车主模型复杂薄壁结构件加工变形，基于变形控制优选装夹布局。董辉跃等[2-3]仿真模拟了装夹位置、装夹顺序和加载方式对框类薄壁工件变形的影响，并优化装夹方案获得较平均的参与应力，减小工件变形。金秋等[4]针对弧形薄壁件铣削加工过程，建立了考虑瞬态铣削力的工件变形有限元模型优化夹紧点位置；武凯等[5]通过建立封闭型腹板铣削加工受力模型、有限元变形评价模型,结合切削试验,研究了薄壁腹板加工变形的基本规律,提出了相应的变形控制工艺措施；Kaye等[6]仿真分析了飞机机翼工件的加工刚性，提供刚性评价结果，为切削参数选择提供依据。李康等[7]通过有限元分析薄壁框类工件加工过程中残余应力对变形的影响，优选变切深切削方式和从内向外的铣削路径提高加工效率和质量。Richter等[8]将实际测量的残余应力值作为输入值用于工件加工变形的有限元仿真分析，这种方法对残余应力测量准确性要求很高。汪振华等[9]采用有限元生死单元技术和移动载荷施加方法模拟材料去除过程，预测薄壁件加工变形。飞机结构件制造过程中结构件种类众多，仿真分析方法难以得到有效应用，工程实用性差。

在优化算法研究方面，郑联语等[10]提出了一种基于模糊理论的评价零件刚性的方法，该方法综合考虑了精度、变形、稳定性和干涉等因素，建立了零件刚性综合评价体系，但是该方法无法预测零件刚性；秦国华等[11]建立了描述加工尺寸与应限制自由度之间关系的自由度约束原理，并提出了定位合理性的判定定理；辛民等[12]以试验数据为训练样本建立了基于BP神经网络的铣削加工变形与铣削参数关系的预测模型；Harman等[13]通过切削试验构建工件尺寸与刚性的关系，利用多种约束条件，评价飞机接头工件的刚性。通过优化算法建立的工件刚性预测模型大多以试验数据作为样本，需要进行大量修正才能应用于工况复杂的结构件制造过程，并且建模过程中缺乏对薄壁结构件典型特征(腹板等)的针对性研究。

综上所述，由于有限元仿真和优化算法研究的局限性，目前在飞机结构件生产制造过程中缺乏能够有效应用的刚性评价方法。目前在飞机制造企业中，工件刚性主要是基于经验值评价，缺乏理论依据和数据支持，评价结果因人而异。因此，如何准确快速评价工件刚性成为飞机结构件加工生产过程中亟需解决的难题。

框梁类结构件作为典型飞机结构零件，具有壁薄、尺寸大、结构复杂等特点，衡量框梁类工件在加工过程中刚性强弱的关键是对工件腹板刚性的准确把握。腹板是框梁类飞机结构件的重要加工特征，腹板刚性强弱是选择装夹方案需要考虑的重要因素，同时也是腹板自身加工切削参数选择的参考依据。根据结构特征不同可以将腹板分为封闭型腹板和开敞型腹板，如图1所示。本文通过研究飞机结构件封闭型腹板和开敞型腹板的结构特性，考虑铣削过程中工件腹板受垂直腹板方向切削力作用，基于简支梁及悬臂梁弯曲变形力学模型，建立了一种工件腹板刚性评价理论模型，进而给出了一种精确评价腹板刚性的方法，然后进行腹板刚性有限元仿真分析，验证了腹板刚性评价理论模型的准确性。

1 基于梁弯曲理论的腹板刚性评价模型

根据弯曲变形的理论，当梁受到垂直于其轴向的集中载荷时会发生弯曲变形，其抗弯刚性可表示为：

K=E·Iz

(1)

式中：E为材料的杨氏模量；Iz为梁的截面相对于中心z轴的惯性矩，可用式(2)表示：

(2)

若截面形状为矩形，且矩形的长度为m(图2中z方向)，宽度为n(图2中y方向)，则其截面相对于z轴的惯性矩可表示为：

(3)

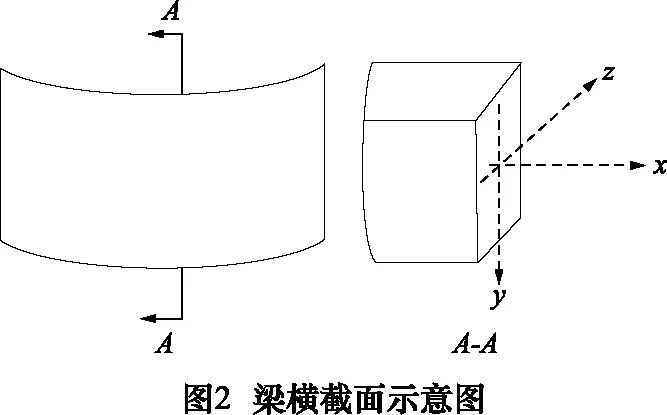
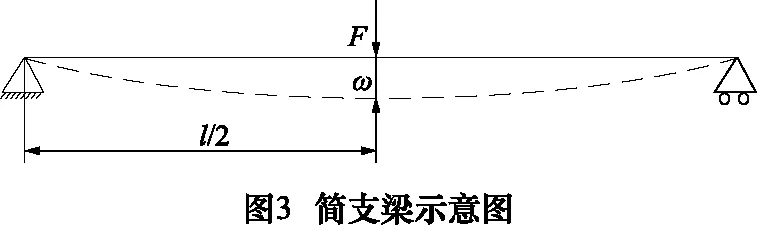
不同约束形式的梁在垂直于梁长度方向内承受不同载荷时其变形量不一样，而工程应用中最关心的是最大变形量。一般而言，在刚性最弱的地方为力的作用点时，变形量最大。结合工程应用实际，本文主要考虑简支梁(图3)和悬臂梁(图4)模型，简支梁的最大变形量ω发生在梁长度方向的中点，可以表示为：

(4)

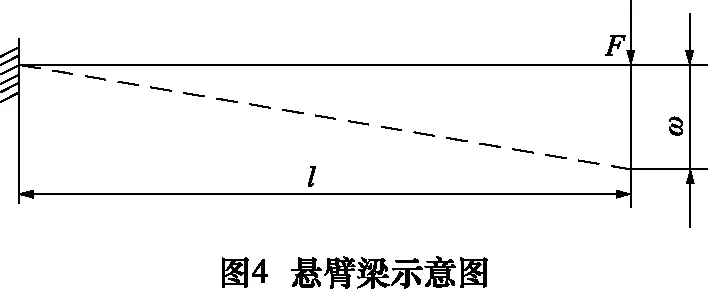
悬臂梁的最大变形量ω发生在离支撑距离最远端，可以表示为：

(5)

式中：F表示梁受到的集中载荷；l表示悬臂梁长度；ω表示梁的最大变形量；Ki表示梁的抗弯刚性。因此，不论是简支梁还是悬臂梁都可以用Kl=k·EI/l3表示梁的最弱抗弯刚性。显然，梁的最弱抗弯刚性与梁截面惯性矩Iz成正比，与刚性最弱点到约束点距离l的三次方成反比，k表示不同梁模型的抗弯刚性系数,对简支梁系数k=48，悬臂梁系数k=3。

飞机结构件在数控加工过程中，其腹板主要受垂直于腹板的切削力作用，可简化为集中载荷，而腹板的形式则因零件的结构不同而存在多种结构形式。但是，整体来看，单个的槽腔腹板结构特征主要可分为封闭型(封闭槽)和开敞型(开口槽)两种。针对这两种具体结构，理论模型如下：

1.1 封闭型腹板刚性评价

图5是一种四周全封闭的槽腔结构，为简化问题，可假设该槽底腹板厚度处处相等，用t表示。该腹板在加工过程中其刚性最弱处为其几何中心O。要保证该腹板区域的刚性满足加工要求，只需保证O点的刚性满足要求即可。因此，工程应用过程中只需评价O点的刚性即可。

由于该腹板为全封闭区域，可等效为四周全约束。为计算O点的刚性，把该腹板微分成无数个简支梁，加工过程中刀具的作用力垂直于梁的长度方向，梁主要承受弯曲载荷。因此，评价O点的刚性转化为评价其抗弯刚性，可先计算出每一段梁在其中点O的抗弯刚度为：

(6)

若该梁的长度可以表示为s的函数l(s)，则：

(7)

在腹板区域积分，即可得到封闭型腹板区域O点的总体抗弯刚性为：

(8)

1.2 开敞型腹板刚性评价

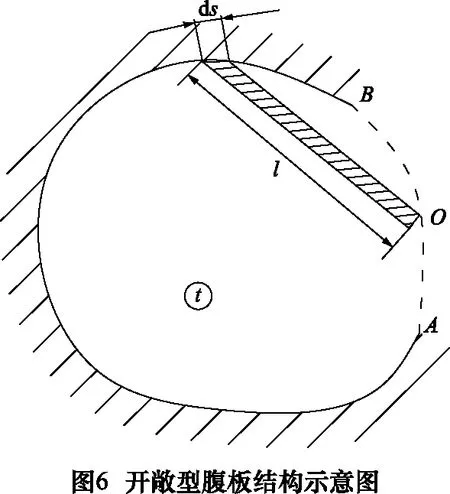
开敞型腹板刚性最弱点O在开口中部某处(图6)，若腹板厚度为t，等效梁的长度为s的函数l(s)，将腹板微分处理，等效成若干以O点为自由端的悬臂梁弯曲模型，当集中载荷作用在O点时，其变形量最大，其抗弯刚性可以表示为：

(9)

沿约束边界(优弧BA)积分得出开敞型腹板在O点处的抗弯刚性为：

(10)

2 腹板典型结构特征抗弯刚度计算模型

飞机框梁类结构件腹板结构特征多以矩形或圆形为主，因此本文以矩形和圆形结构特征为具体实例推导腹板刚性的计算模型。

2.1 矩形腹板

(1)封闭型

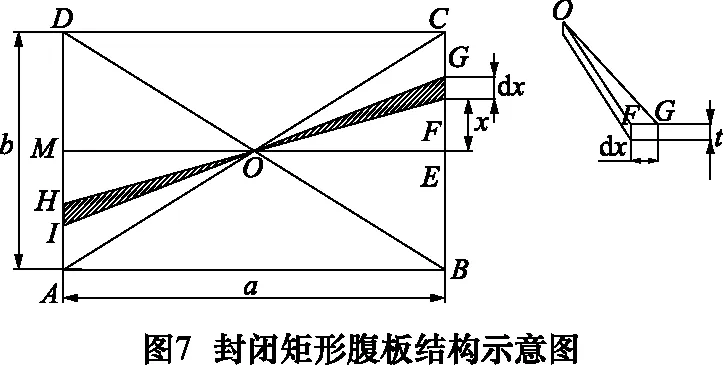
若矩形长度为a，宽度为b(图7所示)，取图7所示FGHI的一段简支梁，则其中点O的抗弯刚性可以表示为：

(11)

将式(11)在图7所示ECAM区域内积分：

(12)

由对称性可知，O点在长度方向(图7所示尺寸为a的方向)的抗弯刚性为：

(13)

同理可推导矩形框宽度方向的抗弯刚性为：

(14)

故全封闭的矩形框的总体抗弯刚性可表示为：

(15)

(2)开敞型

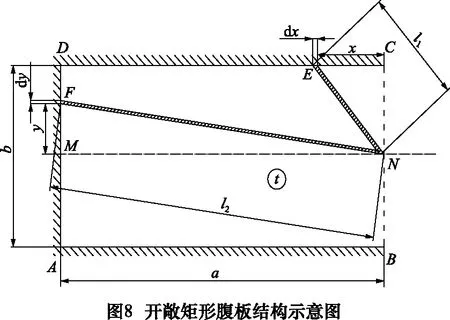
如图8矩形腹板ABCD的一段BC开口，腹板的厚度为t，由几何结构可知，当集中载荷作用在开口的中点N时，N点的变形量最大。根据该腹板特征结构，该腹板可微分成两种类型的悬臂梁，一种是以长度方向为固定端(CD方向)，N点为自由端的梁EN，另一种是以宽度方向(AD方向)为固定端，N点为自由端的梁FN。

这两种梁N点的抗弯刚性可以分别表示为：

(16)

(17)

对式(16)、(17)分别沿固定端边界积分得沿宽度方向和长度方向的刚性为：

(18)

(19)

由对称性可知，开敞型矩形腹板N点的抗弯刚性可表示为：

KN=2KNb+2KNa

(20)

2.2 圆形腹板

(1)封闭型

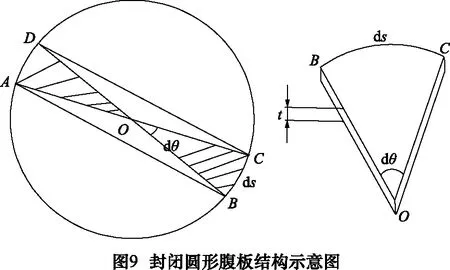
若圆形半径为R，取如图9所示的ABCD的一段简支梁，则其中点O的抗弯刚性可以表示为：

(21)

对式(21)右端积分得封闭圆形腹板的抗弯刚度为：

(22)

(2)开敞型

如图10所示，假设圆形腹板开敞部分为劣弧MN，由对称性可知，该腹板刚性最弱点为劣弧MN的中点A,腹板厚度为t，圆弧半径为R，取图示阴影部分ABCD的悬臂梁，由几何关系可知，该段梁的长度为：

(23)

当集中载荷作用于A点时，其变形量最大，梁ABCD在A点的抗弯刚性可表示为：

(24)

将式(24)沿优弧NM积分得到该开敞型腹板在A点受集中载荷时的抗弯刚性为：

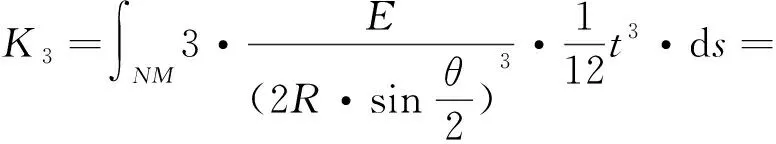
(25)

计算化简得：

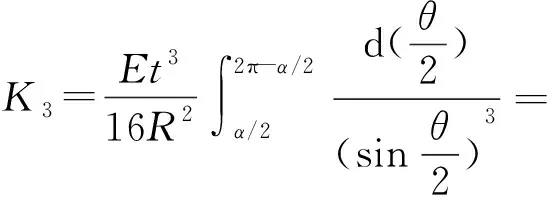
(26)

代入积分上下限得：

(27)

3 有限元仿真切削验证

为验证上述飞机结构件框梁类腹板刚度计算模型的准确性，以矩形腹板为例，使用有限元仿真分析软件ABAQUS，构建具有不同腹板厚度的工件模型，采用生死单元定义余量逐渐去除，同时施加移动切削力载荷，仿真分析腹板变形量。

仿真模型中，封闭型和敞开型矩形腹板的尺寸分别如图11和图12所示，主要由腹板和切削余量两部分组成，其中腹板尺寸设定为L=250 mm,W=200 mm,H=2b+t,a=b=20 mm,t=12 mm、10 mm、8 mm、6 mm、4 mm, 切深ap=2 mm，切宽ae=5 mm。

有限元仿真边界条件和载荷设置如图13所示，在与腹板连接的筋条上施加固定约束，将切削余量划分并使用生死单元设定网格属性，模拟切削余量的去除过程，同时在生死单元上施加切削力载荷，切削载荷随切削余量去除不断移动。

仿真模型网格使用C3D20R二十结点二次六面体单元，工件材料采用铝合金7050-T7451，物理性能如表1所示，使用Johnson-cook模型设定材料应力应变关系，详细参数如表2所示。

仿真模型中施加的切削力载荷根据试验测试得到的z向切削分力设定，切削参数及切削力测量结果如表3所示。

表1 铝合金7050-T7451材料属性

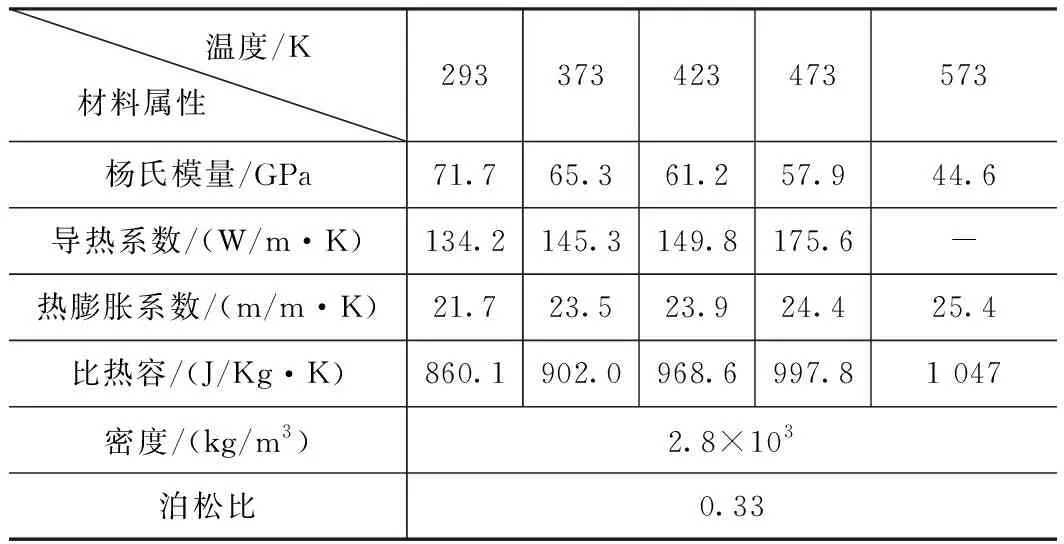
温度/K材料属性 293373423473573杨氏模量/GPa71.765.361.257.944.6导热系数/(W/m·K)134.2145.3149.8175.6-热膨胀系数/(m/m·K)21.723.523.924.425.4比热容/(J/Kg·K)860.1902.0968.6997.81 047密度/(kg/m3)2.8×103泊松比0.33

表2 铝合金7050-T7451 Johnson-cook模型参数

材料牌号A/MPaB/MPanCm7050-T7451441383.40.250.0111

表3 试验切削参数和切削力

切削速度/vc/(m/min)每齿进给fz/(mm/齿)轴向切深ap/ mm径向切深ae/ mm轴向切削力Fz/N7500.1445254

封闭腹板加工变形仿真云图如图14所示，随着刀具移动腹板加工变形先增大后减小，当刀具切削到腹板中间时腹板变形最大，z向变形量为0.551 mm。

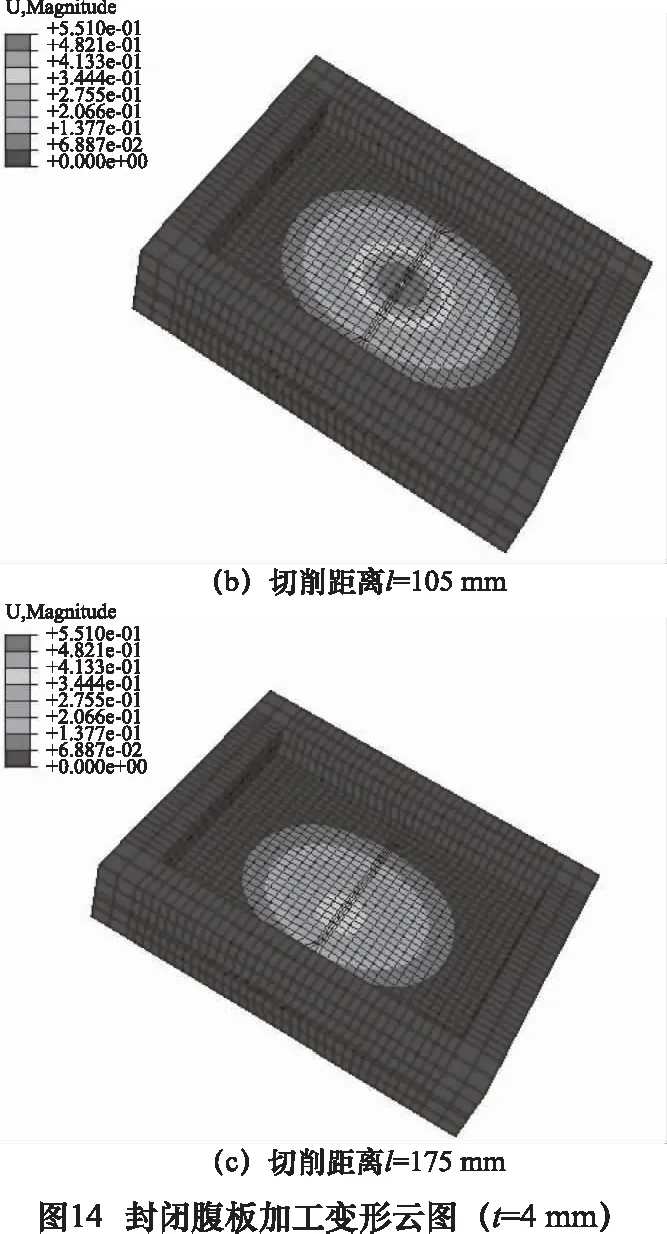
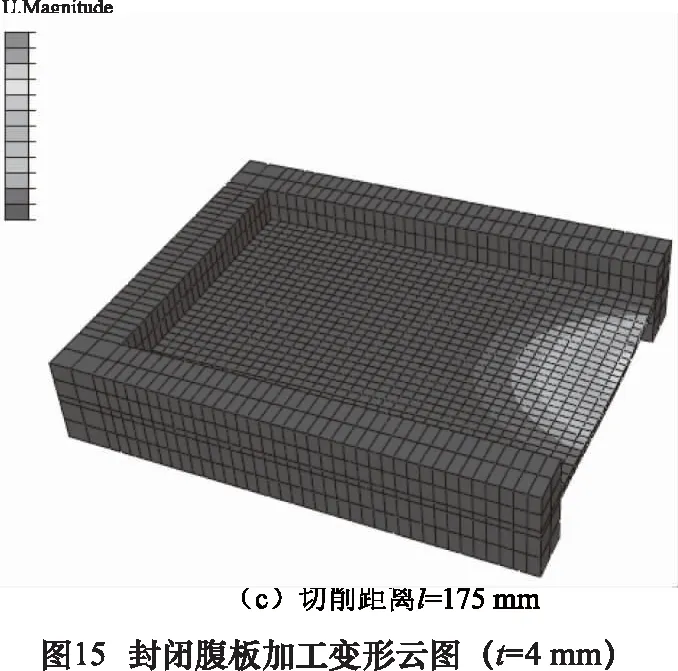
敞开腹板加工变形仿真云图如图15所示，z向最大变形量为1.390 mm。

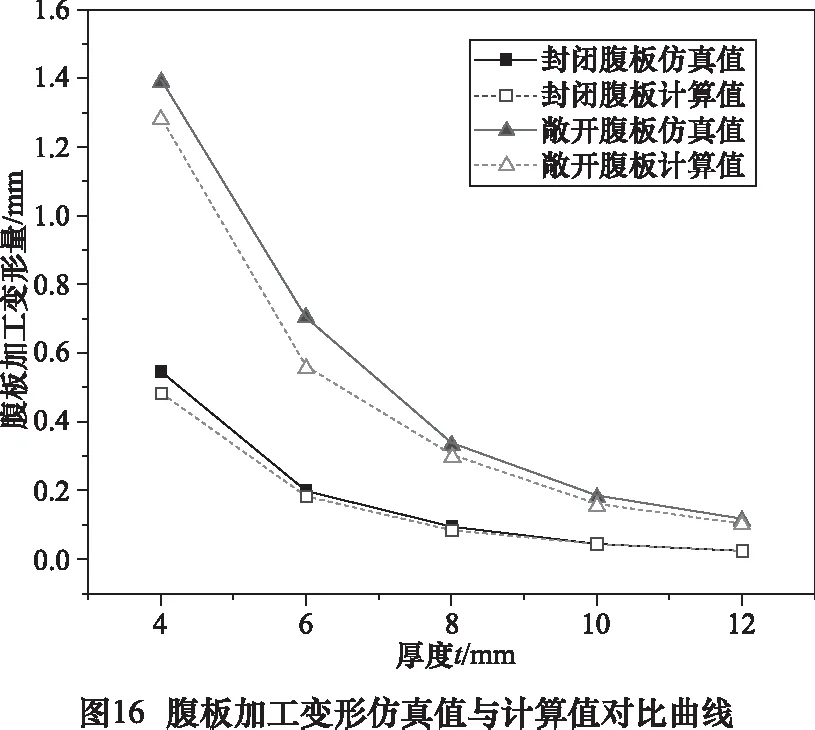
记录不同厚度封闭腹板和敞开腹板加工最大变形量的仿真结果，与本文刚度评价模型的计算结果比较，如图16所示。

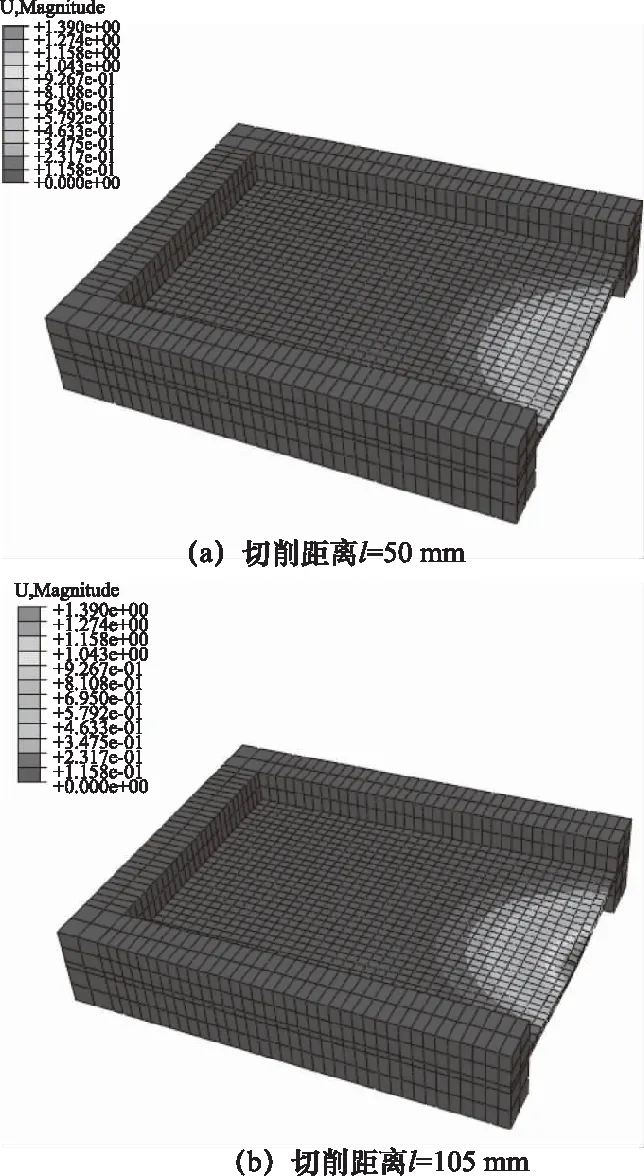
对比分析有限元仿真和刚度计算模型结果，仿真得到的矩形腹板刚性最弱处与计算所得腹板刚性最弱位置基本一致，变形量计算值与仿真值的偏差小于10%，证明通过本文腹板刚性评价模型可以快速精确地评估腹板加工变形，指导加工工艺方案制定与实施。

4 结语

飞机框梁类工件结构复杂，其广泛存在的弱刚性结构，对装夹设计、工艺方案制定带来了极大的难度。工件刚性的判定对工人的经验依赖程度大，而目前对刚性的研究成果工程实用性还不强。因此，本文提出了一种基于梁弯曲力学变形模型求解飞机结构件腹板刚性的方法，得到飞机结构件封闭型腹板和开敞型腹板结构的抗弯刚性，并以矩形和圆形腹板结构为例进行了刚性计算，为进一步判定工件整体刚性、优化装夹方案及切削参数提供了理论参考。本文主要做了以下工作：

(1)结合典型飞机结构件的主要特征即腹板特征，以梁弯曲变形力学模型为基础，将力学模型和工程实践相结合，建立了一种腹板刚性评价的理论模型，进而给出了一种精确评价腹板刚性的方法。

(2)给出了飞机结构件封闭型、开敞型腹板抗弯刚性通用计算方法。

(3)以矩形、圆形腹板为例，给出了具体的腹板刚性计算公式。