基于分形几何理论的微气体轴承承载特性研究*

2018-08-13李恒娟王俊青石凤琴

制造技术与机床 2018年7期

李恒娟王俊青石凤琴

(北京城市学院机械工程系，北京101300)

随着微机电系统(MEMS)技术的高速发展，微流体装置也得到广泛应用，其中微气体轴承由于具有摩擦损耗小、精度高、结构简单等优点，被广泛应用于精密机床、医疗器械、电子精密仪器等旋转机械领域[1-2]。然而，微尺度条件下气体的流动特性与其他宏观层面的普通流体截然不同[3]。因此，基于超薄气膜润滑技术对微气体轴承流动特性研究将显得尤为重要。

目前对于超薄气膜润滑理论的研究主要基于气体稀薄效应的影响，从而通过速度滑移模型对Reynolds方程进行修正，但很少涉及表面粗糙度对微气体轴承润滑特性的影响[4]。由于微气体轴承间隙处于微米量级，表面粗糙度的影响效应将不可忽略。因此，综合考虑表面粗糙度与气体稀薄的耦合效应对微气体轴承性能进行研究，将具有重要的理论意义。

本文通过综合考虑分形粗糙表面与稀薄气体的耦合效应，推导出引入速度滑移边界的超薄气膜润滑Reynolds方程，并使用有限差分法对其进行离散求解，从而对比研究光滑表面与粗糙表面两种情况下，不同参数对气膜压力分布、承载能力的影响规律。

1 分形粗糙表面的表征

Mandelbrot首先引入分形几何的概念，其可以用来表征微尺度器件以及工程应用中的随机和多尺度拓扑结构，并且可以用分形维度来描述物体的随机性与不规则性[5]。

Majumdar和Bhushan发现实际的工程粗糙表面可以由分形几何表征，为了阐释分形粗糙表面的连续性、不可微性以及自仿射性，其表面轮廓用Weierstrass-Mandelbrot(W-M)函数可表示为[6]：

(1)

式中：G为表面缩放常数；Df为表面轮廓的分形维数(1﹤Df﹤2)；γ为谱密度和自仿射特性的比例参数，一般取γ=1.5；n1为低截止频率，其值取决于表面轮廓样本长度Ls，且γn1=1/Ls。

随着Df幅度的减小或者G的幅度增加，将会产生更加粗糙且无序的表面形貌。由于W-M函数可由无限个频率模型叠加而成，因此，随着W-M函数空间频率ω的变化，可以用平均功率谱密度函数S(ω)表示为：

(2)

功率谱密度函数可以用原子显微镜试验获得，考虑到粗糙高度与分形维数Df、比例常数G的关联性，则均方根粗糙高度σ的表达式为：

(3)

式中：ωl为低频极限，其值取决于表面轮廓样本长度Ls,ωl=1/Ls；ωh为高频极限,其值ωh=1/Lr，Lr为扫描仪器分辨率。

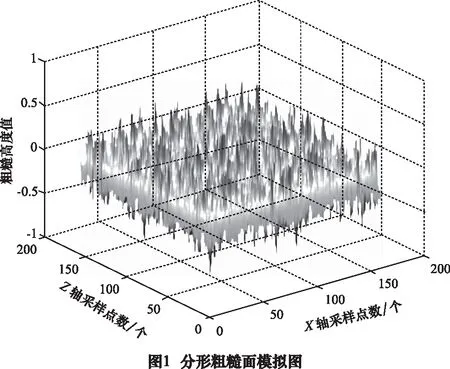
根据式(1)对分形粗糙面进行模拟，设置X、Z方向的采样点个数为200，如图1所示，对于工程粗糙面样本，可以通过结构函数来确定分形维数Df，并通过引入轮廓仪扫描的均方根粗糙高度值来确定比例常数G，从而根据Df和G来表征W-M函数。

2 数学模型

2.1 物理模型

本文主要以微机电系统(MEMS)中的微气体轴承为研究对象，如图2所示。

2.2 边界条件

基于超薄气膜润滑理论，假设平板沿x方向的相对速度为Uplate，并且沿z方向的速度为零，同时假定气流温度是均匀恒定的，并与环境温度保持一致。则气流滑移模型沿x、z方向的表达式为[7]：

(4)

其中：

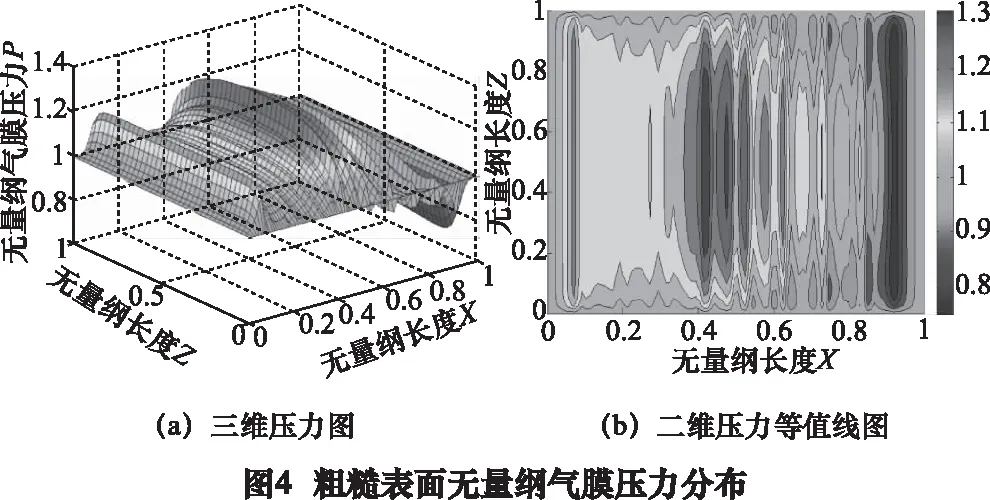
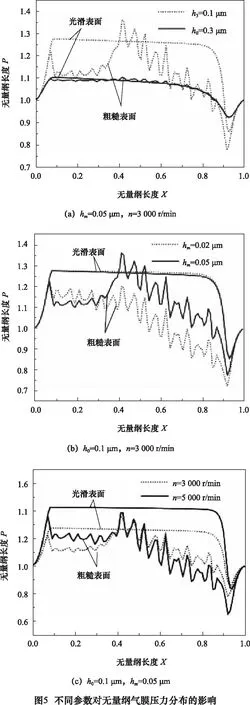
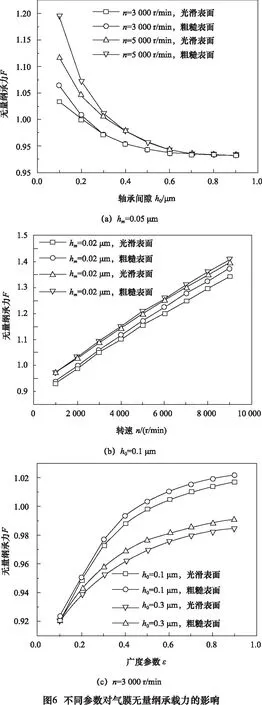
式中：u、v分别为x、z方向的气流速度；λ为气体分子平均自由程；ϑ=min[1/Kn,1]，α为调节系数，Kn为努森数(0.01

2.3 修正的Reynolds方程

根据微间隙内气流流速分布状态，其润滑方程可以表示为[8]

(5)

式中：p为气膜压力；μ为气体动力黏度。

结合广义的速度滑移边界方程(4)对方程(5)进行积分，则速度场方程分别为

(6)

式中的h表示气膜厚度，则沿着x方向的气膜厚度变量h(x)主要由两部分构成。

h(x) =hs(x)+hr(x,G,Df)

(7)

式中：hs(x)为光滑表面的膜厚度变量；hr(x)基于平均水平的随机变化测量值。

根据式(6)中的压力流速的速度分布，可以将归一化Poiseuille流量QP表示为：

(8)

考虑到微气体轴承的稳态可压缩过程，则无量纲Reynolds方程可以简化为[9-10]

(9)

其中所引入无量纲参数及变量包括：

(10)

其中，

(11)

求解方程(9)时，所引入的边界条件为：

(12)

2.4 数值求解方法

通过有限差分法对修正的Reynolds方程(9)进行离散求解，并对气膜内部各节点中差分近似求导，同时采用高斯-赛德尔迭代法进行计算，其中迭代过程中所采用的收敛准则为

(13)

3 计算结果分析

本文在计算中所采用的微气体轴承初始操作参数如表1所示。

表1 微气体轴承初始参数

参数数值轴承气膜长度L/μm10.0轴承气膜宽度B/μm10.0台阶长度xstep/μm4.0台阶深度hm/μm0.05最小气膜厚度h0/μm0.1圆角半径r/μm1.0动力黏度μ/(Pa·s)1.79×10-5转速n/(r/min)3 000

3.1 不同参数对气膜压力分布的影响

图3、图4分别示出光滑表面与粗糙表面情况下无量纲气膜压力分布图。经过对比可以发现，当考虑表面粗糙度时，由于分形粗糙面的存在，气膜压力产生随机波动，且在阶梯位置X=0.4附近波动较为强烈，且达到最大压力峰值，其中最大压力值较光滑表面提升6.7%，同时压力分布呈现出随机性和非线性，并相对Z=0.5轴对称分布。

为了进一步探讨粗糙表面下不同结构参数对压力分布的影响，图5示出不同轴承间隙、台阶深度以及转速对气膜长度方向压力的影响。通过对比光滑表面与粗糙表面两种工况发现，表面粗糙度对气膜压力分布的影响不可忽略。由图5a可以看出，随着轴承间隙的增加，气膜整体压力水平有所降低，并且气膜厚度越小，其压力波动越强烈。其原因在于：表面粗糙度与气体稀薄效应耦合时，气膜厚度减小将导致Knudsen数增加，从而气体稀薄效应增强，此时表面粗糙度的影响效应也将显著增强，从而使得压力产生强烈的随机性波动。相比于光滑表面工况，当最小气膜厚度h0分别为0.1 μm和0.3 μm时，其最大压力值分别提升6.7%、1.2%。从图5b可知，当表面光滑时，台阶深度对压力几乎无影响；当考虑表面粗糙度时，气膜压力波动曲线一致，当处于X=0.3 μm附近时，压力分布出现分界点；当hm分别为0.02 μm和0.05 μm时，对比两条粗糙度压力曲线，其最大无量纲压力值分别为1.21、1.36。通过图5c可以发现，当考虑表面粗糙度时，转速对气膜最大压力的影响较小，当转速n=5 000 r/min时，相比于3 000 r/min的工况，其光滑表面时最大无量纲压力提升11.2%，然而粗糙表面时最大无量纲压力变化幅度为0.002。

3.2 不同参数对气膜承载力的影响

图6示出了光滑表面与粗糙表面两种情况下，无量纲气膜承载力随着不同轴承间隙、转速及广度参数的变化规律。从图中知道，无量纲承载力随轴承间隙的增大而减小，随转速和广度参数的增大而增大。由图6a可知，当最小气膜厚度h0小于0.3 μm时，表面粗糙度的影响效应增强，相比于光滑表面，其承载力有所提升，其中转速越大，承载力的提升幅度越显著；随着轴承间隙的增大，表面粗糙度与稀薄气体的耦合效应将减弱，气膜承载力也将减小；当h0=0.1 μm，n=5 000 r/min时，相比于光滑表面，此时无量纲承载力提高7.2%。由图6b看出，承载力与转速近似正比例关系，但台阶深度对其承载力的影响不大；当hm=0.05 μm时，相比于光滑表面，其无量纲承载力相对变化幅度最大为0.04。从图6c发现，随着广度参数ε增加，其有效承载区域将增大，承载力也随之增大，最后趋于平缓；此时轴承间隙越小，其承载力相对变化幅度越显著。