基于仲裁器物理不可克隆函数的稳定响应选择

◆尹魏昕 高艳松 贾咏哲 徐 雷

基于仲裁器物理不可克隆函数的稳定响应选择

◆尹魏昕1高艳松2贾咏哲2徐 雷2

(1.国家计算机网络与信息安全管理中心江苏分中心 江苏 210003；2.南京理工大学计算机科学与工程学院 江苏 210094)

物理不可克隆函数（PUF）利用制造过程引入的不可控差异作为芯片的指纹信息。PUF的典型应用有认证、验证及密钥生成，对于一个强PUF，其还可以用于密钥交换以及比特承诺。上述应用中，都需要PUF具有高稳定性。本文提出一个方法，无需使用大开销的片上纠错逻辑来对不稳定响应纠错，亦无需存储纠错所必须的辅助数据。我们使用两个APUF数据集的测量值来验证我们的方法，实验结果表明，在最坏情况下，即使PUF响应的错误率达到16.68%，也能根据需要产生大量的稳定响应。

稳定响应；PUF；模型建立

0 引言

物理不可克隆函数（Physical unclonable functions, PUF）是新型的低成本硬件安全原语，并且能够在设计和制造过程中[1]作为不可分离的信任根被无缝地集成到芯片中。PUF是利用制造过程中引入的不可控制的随机差异来提取器件的指纹信息，因此，即使是同一个制造商也无法制造出两个完全相同的PUF。基于延时的PUF[1]，尤其是仲裁器PUF（APUF）和它的变体（例如XOR-APUF）是目前最为流行的硅技术PUF之一。这主要是因为APUF结构紧凑，面积开销小，更为重要的是它能产生大量的激励响应对，因此APUF经常被归类于强PUF[4]。

PUF的主要应用包括身份验证和密钥生成[1]。同时强PUF往往被应用在更高级的密码协议中，例如密钥交换、不经意传输、比特承诺和多方计算[5]。尽管身份验证能够容忍一定的PUF响应噪声，但是密钥生成、密钥交换以及最近的高级密码协议[5]都需要大量稳定的响应。

我们提出利用APUF模型来筛选稳定响应的方法，该方法能够：（1）避免在嵌入PUF的芯片上使用开销较大的纠错逻辑；（2）消除辅助数据的计算以及随之产生的片上存储或片外存储和加载。

我们的工作总结如下：

（1）我们利用APUF的模型来评估一个随机激励的响应可靠性，并以此选择能在所有操作环境下生成稳定响应的激励。

（2）我们在两个APUF数据集上验证了我们的方法，结果显示，在大范围操作环境下再生响应时，没有出现任何错误。

1 相关工作

稳定PUF响应的任务通常由纠错码（ECC）完成。这种方法能够满足单个或少数密钥提取的要求，比如从SRAMPUF中提取一个密钥[7]。

基于ECC的方法能有效保证生成单个密钥的稳定响应，但是，如果需要多个密钥进行：(1)密钥更新；(2)密钥交换；(3)受控的PUF结构[2]，这种方法的开销将变得较大。

文献[8]用仿真数据建立了基于延迟的PUF可靠响应的选择方法，并进行了相关研究。但是确切PUF操作环境（如工作电压和温度）对选择策略的影响仍有待研究。因此我们根据实际测量数据，大量评估了大范围操作环境下本文提出的稳定响应生成方法。

2 稳定响应选择

2.1 仲裁器PUF

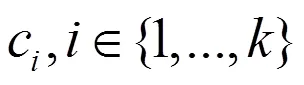
2.2 响应的稳定度

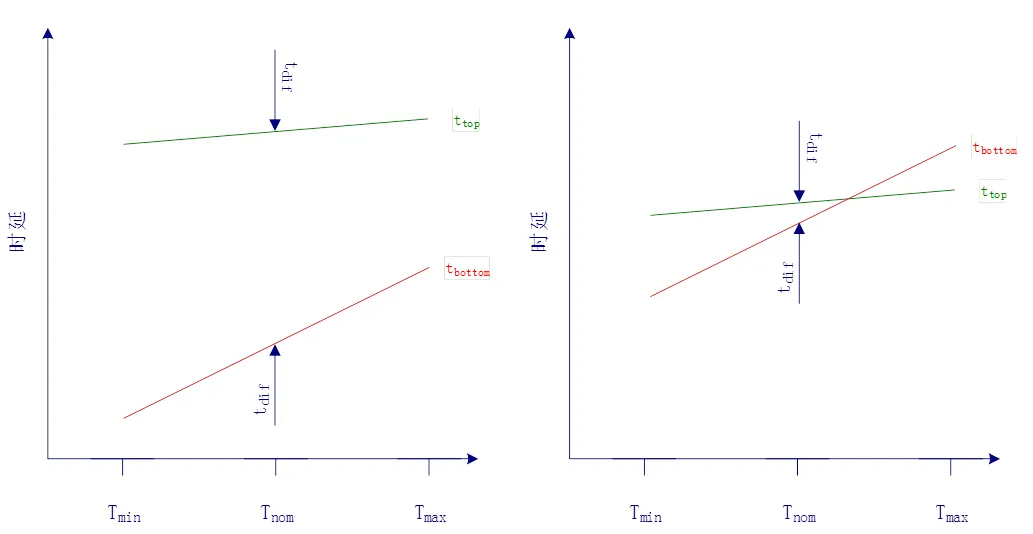
图1 延迟时间关于温度的函数

2.3 构建一个APUF模型

2.4 确定可靠激励

一旦获得了模型，筛选可靠的响应就变得明确而简单，并且这是由服务器在注册阶段一次性完成的任务。最重要的是，集成了PUF的芯片不需要额外面积和功率上的开销，同时也避免了在密钥注册和重构阶段与ECC和辅助数据相关的开销。下表1算法1中描述了激励筛选程序。

表1 激励筛选程

3 实验验证

在本节中，我们用两个不同数据集来验证所提方法：

（1）我们使用ROPUF[11]频率的测量值来合成APUF，通过这种方式，我们可以获得几乎任意数量的CRP用来做大范围的测试。

（2）我们使用从8个FPGA上实现的8个APUF中的CRP数据[12]（该数据集中的CRP总数为64000）。但是我们认为，测试合成的APUF需要获得足够数量的CRP，因为64000个CRP可能不足以进行某些测试。例如，通过使用第一个数据集，我们可以测试从8.3×108个随机激励中筛选出来的多达5×107个可靠的激励，它们都产生了稳定响应。而如果使用第二个数据集，筛选出来的CRP数量可能极少，无法满足数量上的要求。

构建APUF的模型只需要在标准操作环境下而不是所有操作环境下收集一定数量（10,000个）的CRP。对于64级APUF而言，一个CRP的评估需要50ns的时间，CRP收集的时间不到1s，因此只需要不到15s就可以获得一个模型[3]。我们使用MATLAB 2012b来实现模型的构建，处理器是一个Intel i7-3770CPU@3.4GHz的CPU。

3.1 数据集描述

第二个CRP数据集是从8个PDL（可编程延迟线）APUF获得的，每个PDL APUF有128级，此公开数据集有64000个CRP[14]。在相同的操作环境下，对每个CRP评估128次。总共考虑9种操作环境：（5℃，0.95V）；（5℃，1.00V）；（5℃，1.05V）；（35℃，0.95V）；（35℃，1.00V）；（35℃，1.05V）；（65℃，0.95V）；（65℃，1.05V）；（65℃，1.05V）。我们将（35℃，1.00V）作为参考操作环境。

3.2 合成的APUF的结果

我们估计了每个APUF的错误率（BER）。BER是指，在同一个PUF上使用同一个随机选择的激励，两次不同的随机评估产生了两个不同的PUF响应的概率。实际上，一般总是使用在参考操作环境下的参考响应，文献[15]进行了不同的操作环境下再生响应与参考响应的比较。我们的测试中，在相同的操作环境下，每个响应被评估100次，结果如图2所示。当电压和温度都处于参考操作环境（电压为1.2V，温度为25℃）时，由噪声单独造成的BER约为2.2%。我们可以看到，与温度相比，电压对APUF的BER有显著的影响。此外，可以看到当电压低于参考操作环境的20%时，得到最坏情况下的BER为12.98%。尽管这里评估的APUF是合成的，但是所得到的稳定性表现与文献[15]非常吻合。

图2 不同电压和温度下的比特错误率（BER）

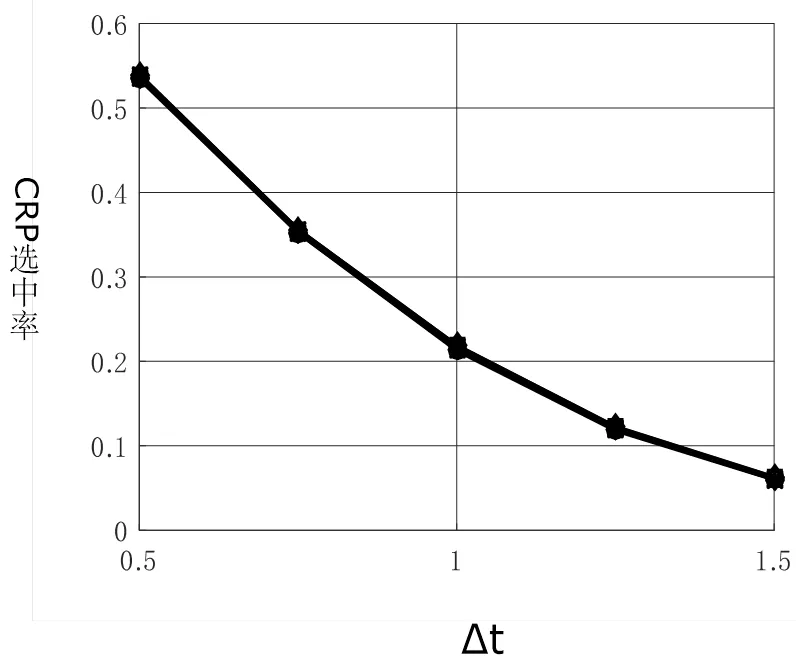
图3 由于筛选可靠激励导致的CRP选中率降低

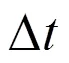
表2 BER@.合成APUF的操作环境范围：电压（0.96-1.44V），温度（25℃-65℃）

4 结论

我们提出了一种确定稳定响应的方法，即使它们在大范围操作环境下被再生，也不会出现错误。我们提出的方法可以被用到受控的PUF设计中，并且能针对高级密码应用的需求提供大量的稳定响应。由于没有涉及ECC和辅助数据，这种方法对于嵌入了PUF的芯片不造成任何额外开销，模型构建的任务由服务器完成，因此只需要向服务器请求极少的计算资源。大量的实验验证了我们的稳定响应方法的可行性。以下介绍一些未来值得进行的工作，首先，尽管在考虑老化效应的情况下，我们已经证明了仿真数据[8]能产生不错的结果，但还需要做进一步的实测验证。其次，将我们的稳定响应生成方法引入受控PUF中[6]，在这种情况下，必然要提高CRP选中率，因为低CRP选中率将导致需要在受控PUF内实现有效的控制逻辑。最后，同样重要的是，对能生成大量的密钥且不使用辅助数据的密钥生成器，由辅助数据协助的攻击难以对其实施，该攻击只能对仅提取单个密钥或极其有限数量的密钥[7]的密钥生成器造成威胁，这将会是安全地使用稳定响应的另一个值得关注的调查。

[1]G. E. Suh and S. Devadas,Physical unclonable functions for device authentication and secret key generation,in Proceedings of the 44th Annual Design Automation Conference. ACM，2007.

[2]B. Gassend, D. Clarke, M. Van Dijk, and S. Devadas, Controlled physical random functions,in 18th Annual Computer Security Applications Conference. IEEE，2002.

[3]D. Lim, J. W.Lee, B.Gassend, G. E. Suh, M. Van Dijk, and S. Devadas, Extracting secret keys from integrated circuits,IEEE Trans. Very Large Scale Integr. (VLSI) Syst, vol. 13, no. 10，2005.

[4]U. Ruhrmair, J. Solter,F.Sehnke, X. Xu, A. Mahmoud, V. Stoyanova, G. Dror, J. Schmidhuber,W. Burleson, and S. Devadas,PUF modeling attacks on simulated and silicon data,IEEE Trans. Inf. Forensics Security, vol.8,no.11，2013.

[5]U.Ruhrmair and M.Van Dijk,PUFs in security protocols:Attack models and security evaluations,” in IEEE Symposium on Security and Privacy (SP), 2013.

[6]B.Gassend, M.V. Dijk,D.Clarke,E.Torlak,S. Devadas, and P.Tuyls,Controlled physical random functions and applications,ACM Transactions on Information and System Security, vol. 10, no. 4，2008.

[7]G.T.Becker,On the pitfalls of using arbiter-PUFs as building blocks,IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 34, no. 8，2015.

[8]X.Xu,W.Burleson,and D.E.Holcomb,Using statistical models to improve the reliability of delay-based PUFs,” in IEEE Computer Society Annual Symposium on VLSI, 2016.

[9]T.Xu,D.Li,and M.Potkonjak,Adaptive characterization and emulation of delay-based physical unclonable functions using statistical models,in Proceedings of the 52nd Annual Design Automation Conference. ACM, 2015.

[10]M. Majzoobi,E. Dyer, A. Elnably, and F. Koushanfar, Rapid FPGA delay characterization using clock synthesis and sparse sampling,in International Test Conference (ITC), 2010.

[11]http://rijndael.ece.vt.edu/variability/main.html.

[12]M.Majzoobi,A.Kharaya,F.Koushanfar, and S. Devadas,Automated design, implementation,and evaluation of arbiter-based PUF on FPGA using programmable delay lines,IACR Cryptology ePrint Archive, vol. 2014，2014.

[13]A. Maiti,J.Casarona, L.McHale, and P.Schaumont, A large scale characterization of RO-PUF,in IEEE International Symposium on Hardware-Oriented Security and Trust (HOST)，2010.

[14]M. Majzoobi, F. Koushanfar, and M. Potkonjak, Techniques for design and implementation of secure reconfigurable PUFs,ACM Transactions on Reconfigurable Technology and Systems, vol. 2, no. 1，2009.

[15]M.Roel,Physically unclonable functions: Constructions,properties and applications,Ph.D. dissertation, University of KU Leuven，2012.

本文得到国家自然科学基金(No.61671244)和中央高校基本科研业务费专项资金资助(No. 30918011204)的支持。