基于高速铁路换乘服务网络的随机用户均衡模型
2018-08-11刘帆洨彭其渊鲁工圆
刘帆洨,彭其渊,鲁工圆,张 斌
(西南交通大学 交通运输与物流学院,四川 成都 610031)
0 引言
目前,高速铁路已经成为我国旅客出行的重要交通方式。高速铁路出行模式主要包括直达模式和换乘模式[1]。旅客出行是基于路径的选择,而出行模式是路径选择的基础,因而高速铁路旅客的出行过程是基于 2 种出行模式的乘车过程的组合。
由于同一条线路上的列车具有较强的相关性和可替代性,而跨线列车的开行增加了每条线路上客流分布的复杂程度,因而列车不同区段的上座率容易受到旅客出行模式和开行方案的影响[2-3]。列车的票额分配是实现列车客流分配的具体表现[4-5]。既有研究多基于单列车或单线多列车,在收益最大化条件下获得列车 OD 区间票额分配[6-7]。而充分考虑成网条件下的换乘因素,可以使旅客在高速铁路网络上换乘顺畅,避免高速铁路网络列车能力的浪费。
成网条件下列车的能力利用本质是基于网络客流分配的用户均衡问题。自 Beckman 等[8]提出以网络均衡来表示最优化之后,许多学者将“均衡”这一概念应用到各种交通网络中[9-10]。然而,用户均衡 (UE) 是假设出行者在进行路径选择时,对当前网络状态和路况信息是完全了解且是完全理性的,可以精确地计算并选择出行阻抗最小的路径[11]。实际上,高速铁路旅客很难完整掌握列车运行的网络信息,除了广义阻抗中的时间成本、经济成本之外,通常还会根据经验和路径感知信息来选择出行路径 (由列车所构成的服务路径),因而旅客对出行列车/路径的选择行为具有随机性,采用随机用户均衡 (SUE)[12]能更好地反映旅客实际出行乘车过程。为此,构造高速铁路换乘服务网络,分析旅客出行阻抗,建立基于 Logit 模型的高速铁路换乘服务网络的随机用户均衡模型,以更好地适用于高速铁路旅客出行路径选择。
1 高速铁路换乘服务网络的构造方法
由于高速铁路旅客出行主要通过乘车来实现物理位置转移,因而列车运行路径是网络构造的基础。就高速铁路旅客出行乘车而言,其过程包括上车、乘车、下车和换乘 4 个过程,可以通过此过程来描述旅客出行路径,构造换乘服务网络。为了方便描述,假设高速铁路线路网络拓扑结构如图 1 所示。
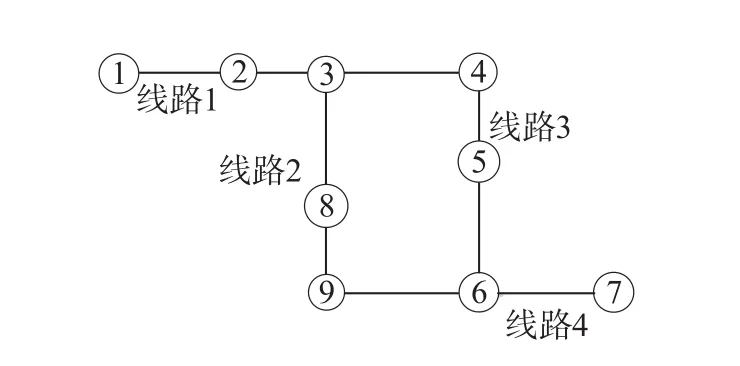
图 1 高速铁路线路网络拓扑结构Fig.1 Train service network
以图 1 为例,出行 OD 为 (1,7),共 4 条线路:线路 1、线路 2、线路 3 和线路 4,各条线路起讫点所形成的运行区间分别是 (1,4),(3,9),(4,6),(9,7)。每条线由停站节点与连接节点的弧所组成。对于每列车都可以依据该列车的开行方案构造一个列车子网络[10]。令H为网络中的列车开行方案编号集,对于任意列车开行方案h∈H,网络中列车开行方案如表 1 所示。
构造开行方案 1 的列车子网络如图 2 所示。图 2中开行方案 1 的列车子网络由节点及和弧段集构成,节点集包括:车站节点和停站节点,车站节点是客运车站对应的节点 (节点 1、节点 2、节点 3),停站节点是车站节点的延伸,表示列车办理乘降作业对应的节点 (节点 10、节点 11、节点 12);弧段集包括:上车弧、乘车弧和下车弧,且都为有向弧。

表 1 网络中列车开行方案Tab.1 Train operation plans in the network
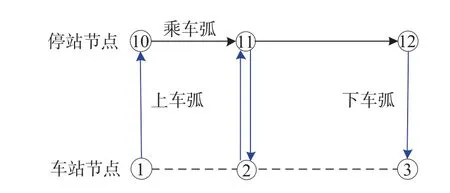
图 2 开行方案1的列车子网络Fig.2 Train sub-network for the fi rst train operation plans
对于换乘的旅客,由于换乘延长了旅行时间,因而换乘对路径的选择有很大影响,相当于延长了实际路程。对不同旅客,在同一换乘站内换乘路径可能是任意 2 个不同开行方案列车之间的换乘路径。由于任意换乘车站的换乘路径是车站内不同站台之间的走行路径,因而任意车站的换乘路径是多路的,但对特定旅客出行路径有惟一换乘弧。将可换乘的车站用星型多路节点来表示,该节点包含一个中心节点、若干换乘节点和换乘弧。其中,中心节点代表换乘车站节点,换乘弧和换乘节点连接不同开行方案列车的列车子网络。将同线换乘和跨线换乘对旅客的阻抗,转化为弧段 (路段) 阻抗。
换乘服务网络由列车子网络和多路节点所构成,记网络为G(V,E),包括节点集V(车站节点、停站节点和换乘站节点) 和弧段集E(上车弧Eu、乘车弧El、下车弧Ed和换乘车站内各站台之间的换乘弧Ea,E =Eu∪Ed∪El∪Ea,其中换乘弧是由旅客接续换乘其他车次增加走行距离而产生,上/下车弧是由旅客在出行区间起讫点上车/下车而产生),W为路网G(V,E) 中所有 OD 对集合,(r,s)为W中起点r到讫点s的 OD 对,(r,s) ∈W,Krs为OD 对 (r,s) 之间所有路径的集合,xe为任意弧段e的流量,e∈E。假设列车都成对开行,只需考虑单向行驶列车即可。
换乘服务网络的构造方法:①用虚线连接各车站,仅用于示意线路。②根据不同列车开行方案生成对应的列车子网络,列车子网络的所有弧段均为有向实线弧。③将网络中非 OD 对起讫点车站之外的其他换乘车站用多路节点来表示;同一车站的换乘节点连接着不同开行方案列车在该站的停站节点,其中多路节点换乘弧的方向与旅客出行路径方向有关,用实线表示物理连通。④将网络中的所有节点 (车站节点、停站节点和换乘节点) 编号。构造换乘服务网络如图 3 所示。
以图 3 中 OD 为 (1,7) 的不同出行路径模式为例,根据旅客出行便利程度将备选出行路径模式分为 4 个优先级,记为prih等级。基于 OD 的出行路径模式优先级如表 2 所示。

图 3 换乘服务网络Fig.3 Transfer service network

表 2 基于 OD 的出行路径模式优先级Tab.2 Priority list of the travel mode based on OD
假设上下车和换乘弧能力不受限制,任意弧段的能力可以表示为
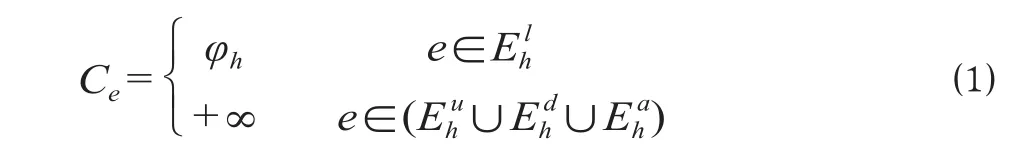
式中:Ce为任意弧段的能力;φh为开行方案h对应列车的定员,即该列车子网络中乘车弧的能力;e为网络中的任意弧段。
2 构建基于换乘服务网络的SUE模型
2.1 换乘服务网络中旅客出行的阻抗函数
高速铁路旅客出行阻抗即为广义出行成本,包括 2 类:由出行时间和费用产生的有形成本,以及由拥挤和心理因素产生的无形成本。换乘服务网络中所有产生阻抗的节点包括停站节点和换乘节点。将停站节点的无形成本用上下车弧阻抗来表达;将停站节点的有形成本 (即停站时间) 包含到节点前方相邻弧段阻抗内 (以列车运行方向为前方),即列车在任意停站节点的停站时间包含到前方相邻弧段乘车时间内。此外,换乘节点阻抗可用换乘弧阻抗来表达。基于此,将所有节点阻抗转换为弧段阻抗,因而网络中只需考虑弧段阻抗。
(1)上下车弧段阻抗。上下车弧段的阻抗主要为拥挤和感知产生的无形成本。上下车的客流量不同,感受的拥挤阻抗不同,可由上下车的时间消耗来表达。
上车弧段阻抗可以表示为
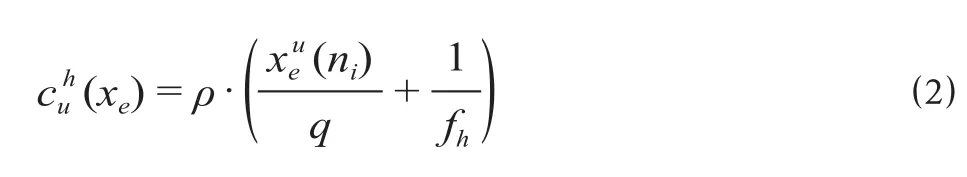
式中:(xe) 为上车弧段阻抗;ρ为高速铁路旅客的平均时间价值;q为旅客上下车的平均客流速度;(ni) 为在对应停站节点ni的上车流量;fh为方案h的列车发车频率。
下车弧段阻抗可以表示为

式中:(xe) 为下车弧段阻抗;(ni) 为下车流量。
(2)乘车弧段阻抗。乘车弧的阻抗包括有形成本 (费用成本、时间成本) 和无形成本 (拥挤成本)。费用成本表示该弧段的票价支出。时间成本表示旅客在弧段e上的乘车时间 (包括相邻后方停站节点的停站时间)。拥挤成本表示旅客在乘车时间内的感知阻抗。当旅客人数在列车定员范围以内,同一车厢内乘坐较少旅客与满座定员人数旅客的情况相比,乘坐较少人数车厢的旅客会因平均活动范围更宽而感受到更优的体验;当旅客人数超过定员时,旅客会因站立疲劳,活动范围缩小感受到额外拥挤,以额外时间开销来表示。乘车弧段阻抗可以表示为
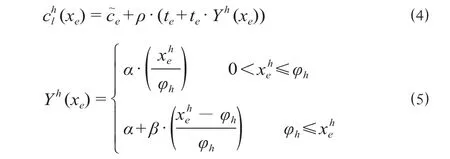
式中:(x) 为乘车弧段阻抗;为弧段e的票价支e出;te为旅客在弧段e上的乘车时间 (包括相邻后方停车站节点的停站时间);Y h(xe) 为列车h单位乘车时间内,因拥挤或感知产生的额外时间开销函数;α和β分别为定员以内和超过列车定员状态下的额外时间开销值。
(3)换乘弧段阻抗。换乘弧段阻抗包括换乘所需的步行时间成本 (有形成本) 和因拥挤或感知产生的阻抗 (无形成本),换乘弧段阻抗可以表示为
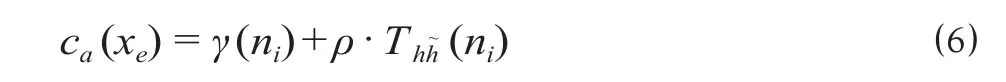
式中:ca(xe) 为旅客在换乘弧段上的阻抗;γ(ni) 为车站ni所在城市等级对应的换乘平均拥挤阻抗;为由开行方案h列车换乘方案列车的平均等待时间。
综上所述,铁路旅客出行总的阻抗可以表示为

式中:wi= {0,1}分别为上车弧、乘车弧、换乘弧和下车弧的有效指标,且对任意wi= 1 表示当前弧段有效,0 则反之。
2.2 SUE 模型的构建
任意旅客对每条路径都有选择的概率,由于不同乘客对同一路径感受到的拥挤阻抗是不同的,可以将其作为随机变量,其中包含确定项和随机误差项。假设随机误差项服从二重指数分布,根据随机效用理论可以得到路径k被选择的概率为

在已知流量条件下,随机均衡配流可表示为

以 Fisk 模型为基础[13]构建基于换乘服务网络的SUE模型,可表示为

为了得到更符合实际情况的路径解,采用梯度投影算法进行求解:①采用K最短路算法生成备选集;②根据实际情况对备选路径再次优选,从而确定网络 OD 对的合理路径集;③基于合理路径集将SUE 模型转化为一个等式约束条件下的最小优化问题进行求解。
3 算例分析
以图 3 所示的换乘服务网络为例,采用 Matlab进行仿真,以验证上述模型的有效性和可行性。
3.1 模型参数标定
换乘服务网络共有 9 个车站节点,令跨线列车的定员为 1 200 人,本线列车定员为 660 人,高速铁路旅客时间价值ρ= 33 元/h,上下车平均客流速度q= 50人/min。票价、区间里程等基础数据如表 3 所示。
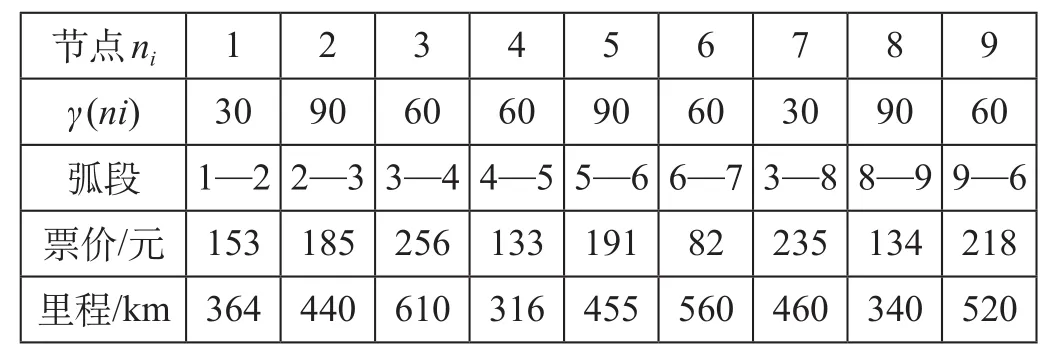
表 3 基础数据表Tab.3 Known conditions
假设列车成对运行,只需考虑单向列车。根据换乘服务网路,需要考虑单向 OD 对,网络中列车开行方案如表 1 所示,旅客出行需求如表 4 所示。
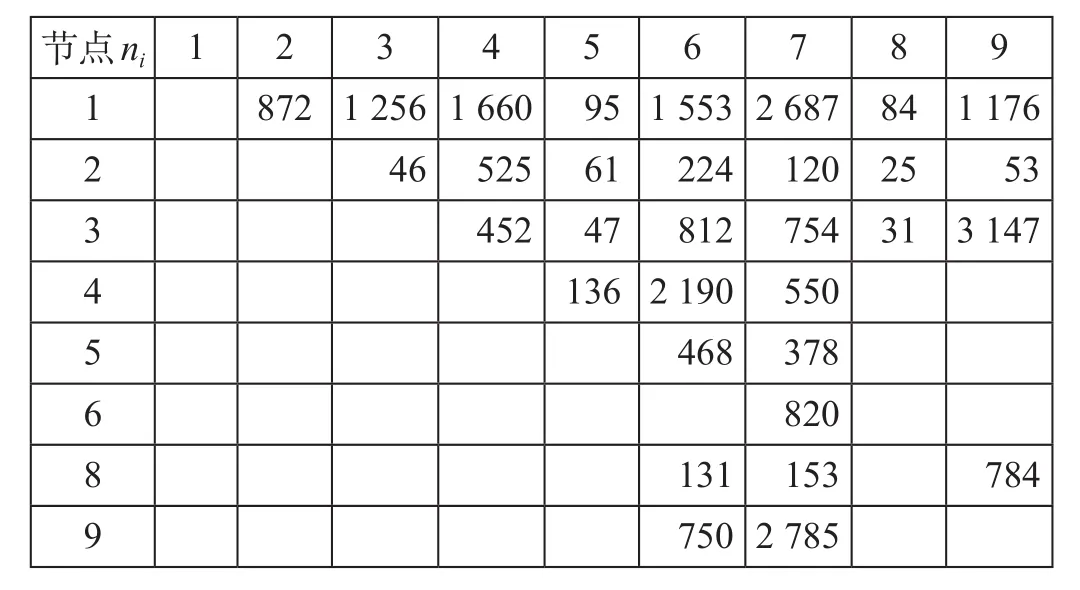
表 4 旅客出行需求表 人Tab.4 Passenger travel demand
对于公式 ⑸ 旅行过程拥挤阻抗带来的额外时间开销系数α= 1、β= 2。参数θ的取值与乘客对铁路客运专线网络的理解程度和同一条路径上的效用值偏差相关,θ值越大,配流结果越接近确定性的用户均衡配流结果[11],因而可调整θ值来适应不同条件下的铁路乘客出行。算例中选取θ= 0.1,表示在考虑旅客出行感知阻抗条件下不同乘客感受到的出行阻抗函数的效用值之间存在较大偏差。
3.2 分配结果
经过网络构造和参数标定,经由模型计算可以得到换乘服务网络的客流分配结果。区间 (1,7) 的客流分配结果对比如表 5 所示。与未考虑换乘条件下的结果进行比较,得到不同方法的列车客流分配结果如表 6 所示。

表 5 区间 (1,7) 的客流分配结果对比Tab.5 Passenger fl ow assignment result for (1, 7)
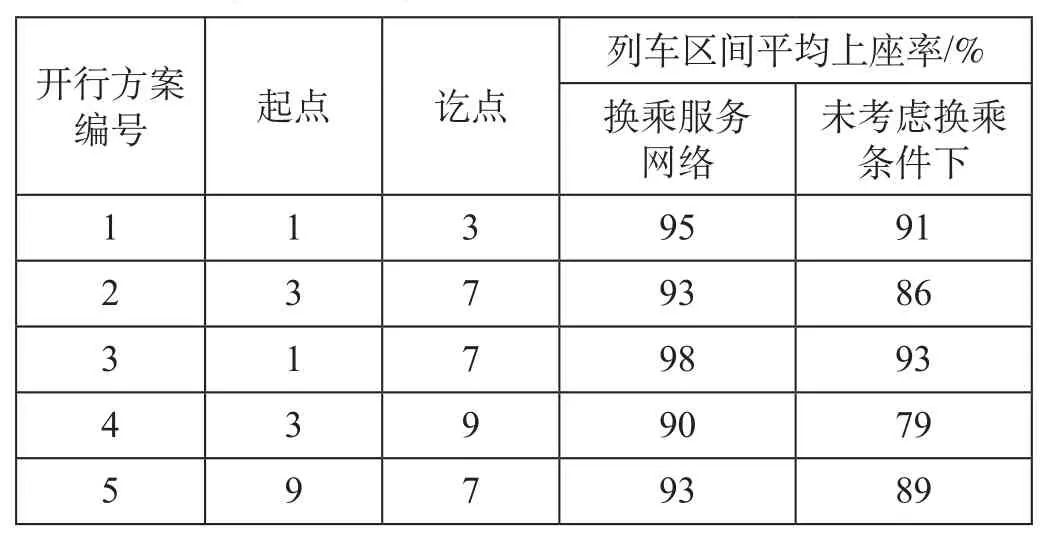
表 6 不同方法的列车客流分配结果Tab.6 Passenger fl ow assignment result for trains with different methods
从表 5、表 6 中可以看出,采用模型可提高区间平均上座率 7.1%,提升客流量 3.5%。换乘服务网络可改善优先级较高出行模式路径上的客流量分配,从而满足 OD 区间更多旅客的出行需求。根据网络不同 OD 客流分配结果,得到列车服务区间下的客流量,从而得到不同开行方案列车的平均区间上座率;与未考虑换乘条件下得到的结果进行对比发现,采用该模型可在一定程度上提高列车区间平均上座率,进而满足更多旅客出行需求,提升服务水平。
4 结束语
随着高速铁路路网规模的扩大,铁路旅客出行需求日益多元化,将多结构、多模式的客流合理分配至高速铁路列车流,是满足旅客需求、提升运输整体效益的重要条件。通过构造高速铁路换乘服务网络,基于该网络构建高速铁路随机用户均衡模型,利用梯度投影算法进行求解,得到网络各区间合理路径下的客流分配。结果表明,模型能够有效描述旅客出行乘车的完整过程,得出不同客流结构和出行模式需求下列车能力利用的有效方式,在一定程度上可提高列车能力利用率,能更好地满足旅客出行需求,提升服务水平,为高速铁路列车客流分配方法的研究提出了一种新思路。
