铁路车站咽喉通过能力分析研究
2018-08-11刘汉英
刘汉英,刘 斌
(兰州交通大学 交通运输学院,甘肃 兰州 730070)
0 引言
咽喉区通过能力在很大程度上影响并决定着整个车站的通过能力,许多学者进行了比较深入的研究。康柳江[1]以铁路大型客运站咽喉区为例研究车站咽喉区进路分配问题,通过分析各种主要影响因素,建立多种咽喉区运用优化模型并求解该模型。杨涛[2]分析了到发线通过能力和咽喉通过能力的具体计算方法及咽喉区道岔的分组原则。于海妹[3]提出并且运用具体实例对坐标计算法和平行进路法在道岔分组中的应用进行分析研究。李非桃[4]分析研究作业进路排列优化方法,提出搜索路径算法,通过运用实例研究咽喉区通过能力计算系统的具体设计原理。刘敏等[5]对车站通过能力进行层次分析。高世蕊[6]结合普速车站通过能力,对客运专线车站通过能力进行研究。刘广武等[7]从走行线通过能力、车辆周转能力、装卸能力等方面分析专用线通过能力的影响因素,并给出相应的计算方法。周楠等[8]运用灰色预测法对一般限制性因素指标发展数据进行研究,提出调整运能分布、提高装卸作业效率等合理化建议。Carey[9]研究大型车站的股道分配及调度问题,采用人工智能的算法对复杂的目标函数进行求解。在这些研究的基础上,以某中间站为例,综合考虑车站调车作业干扰和列车优先等级,运用进路优化方法研究车站咽喉区的通过能力,以提高整个车站的通过能力。
1 铁路车站咽喉区道岔分组及验证方法
铁路车站通过能力包括到发线通过能力和咽喉通过能力[1]。车站到发线通过能力主要与到发线数目和站型有关[2]。咽喉区通过能力与车站咽喉及车场(客车技术整备段和机务段)的布置形式、咽喉区道岔分组和车站到发线的数目有关。道岔分组[3]是为了简化咽喉区的复杂线路,一般遵循大“N”法则进行具体分组[4]。分组完成之后,以单开道岔为例,采用坐标计算法或平行进路法验证道岔分组是否正确合理。
1.1 坐标计算法
坐标计算法如图1所示,首先判断道岔a和道岔b的A段轨道单元(岔根相反方向的轨道单元)的锚点(x1,y1)和(x2,y2)是否在两道岔岔心组成的线段内侧。如果这2组道岔的A段轨道单元的锚点均在两道岔岔心组成的线段外,则说明道岔a和道岔b岔尾相对[5]。接着判断这2组道岔是否分布在线路两侧:首先获得道岔a和道岔b的B段轨道单元锚点的坐标位置,以及道岔a,b的岔心坐标,据此得出直线方程,将B段轨道单元的锚点(x3,y3)和(x4,y4)带入此直线方程,如果同号则两锚点同侧,反之亦然。
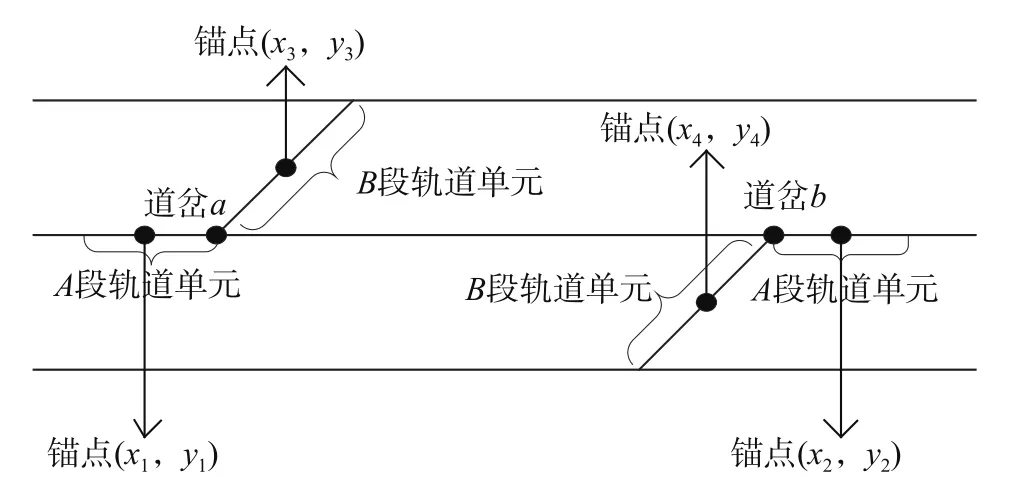
图 1 坐标计算法Fig.1 Coordinate calculation method
1.2 平行进路法
如果2个道岔分别在2条平行进路中,则这2个道岔应分在2个不同的道岔组中[6]。平行进路法如图2所示,道岔a在进路1中,道岔b在进路2中,进路1和进路2构成平行进路,因而道岔a和道岔b分在2个不同的道岔组中,这样就验证了大“N”法则的正确性。如果在各种铁路规章允许的情况下,进路1和进路4、进路2和进路3也可以形成平行进路,同样可以验证道岔a和道岔b应分在不同的道岔组中。
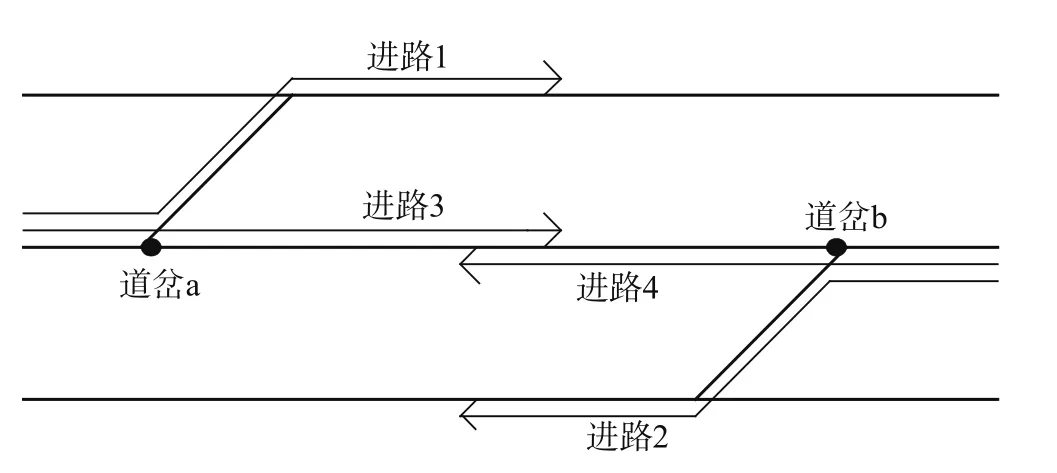
图 2 平行进路法Fig.2 Parallel routing method
在铁路站场咽喉区中,存在着各种各样复杂的道岔,如双开道岔、三开道岔及交叉道岔等,这些复杂道岔都可以使用以上方法分析。
2 铁路车站进路分配方案的选定
选定进路分配方案应遵循2个基本要求[7]:一是到发线的均衡使用;二是合理分配车站咽喉区的平行进路作业。在进路分配方案选定的过程中,运用最大平行进路优化法和最大概率进路优化法进行合理优化。最大平行进路优化法是指在每项作业进行的同时,为后续作业预留最大的平行作业空间[8]。最大概率进路优化法是指在每次排列一项作业进路的同时,最大概率地为后续作业预留进路。通过以下具体分析能够更好地比较出两者的优劣性。
(1)相对于最大平行进路优化法,最大概率进路优化法能够更加准确地判断进路的优劣性。进路优劣性比较如图3所示,a1,a2,…,c5的15个点分别代表15组道岔的岔心,已知两两相邻及对角线的道岔互相连通形成进路。假如图3中有一项作业需要通过咽喉道岔区,从a1点进c2点出,有2条进路可以选择:①a1→b1→c2;②a1→b2→c2。如果选择进路①,则剩下线路的最大平行作业数为3;如果选择进路②,最大平行作业数也为3,因而用最大平行进路优化法分析可得,选择2条进路的效果是一样的。用最大概率进路优化法分析,如果选择进路①,剩余线路可以组成的后续进路有a2→b2→c3,a3→b4→c4等17条;而如果选择进路②,则可以组成的后续进路有15条,与选择进路①相比后续进路少了a2→b2→c3和a3→b2→c32条进路。假设后续进路表示的所有作业都存在,并且概率相等为α,则进路①后续进路的概率为17α,进路②的后续进路概率为15α,从理论上分析,进路①是优于进路②的,由此可得最大概率进路优化法能够更加准确地分配进路。

图 3 进路优劣性比较Fig.3 Comparison of the advantages and disadvantages of routing
(2)运用最大概率进路优化法能够更加准确地模拟现场实际作业情况[4]。在现场实际接发车作业过程中,概率还取决于该列车的重要程度,如军列和旅客列车的优先级都要高于货物列车。进路优劣性比较如图4所示,由于施工原因,a2到c2不能经过道岔b2,因而有2条进路可以选择,即进路①a2→b1→c2和进路②a2→b3→c2。a2到c2的后续作业进路有a1→b1→c1和a3→b3→c3,设概率分别为α1和α2。从优先级别考虑,如果α1>α2,则选择进路②;如果α1<α2,则选择进路①,这样比较即得最大概率进路优化法更加符合现场实际作业情况,能够更准确地指导现场作业。
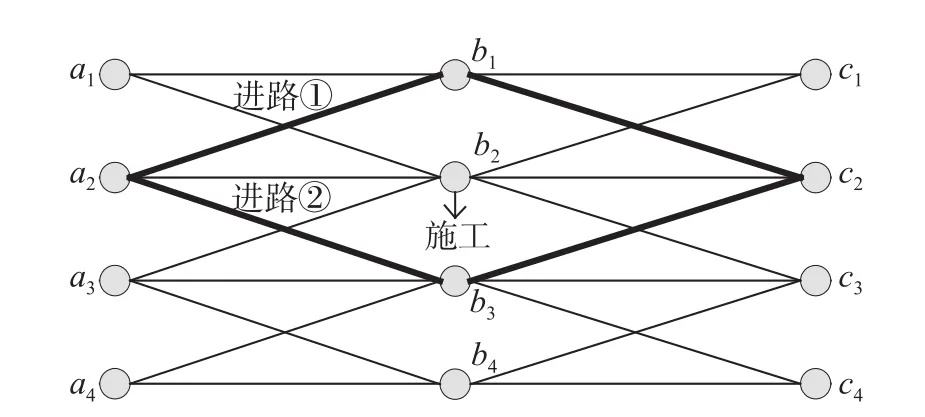
图 4 进路优劣性比较Fig.4 Comparison of the advantages and disadvantages of routing
3 实例分析
3.1 咽喉道岔分组及验证方法的具体运用
以某中间站为例,该站IV道为上行正线,V道为下行正线,1道至9道为到发线,也可以进行调车作业,10道至17道为调车线。1道、V道、6道紧邻站台,可以接发旅客列车,7道、8道、9道可以接发超限列车。某中间站的左端咽喉道岔分组如图5 所示,运用道岔分组的基本原则,左端咽喉区道岔可以分为8个道岔组,用坐标计算法和平行进路法依次验证道岔分组的正确性。
以3号、5号、8号道岔组为例,用坐标计算法验证如图6所示。首先检验3号和5号道岔组,锚点A1和A2均在21号和23号道岔组成的线段外侧,因而2组道岔岔尾相对,同时锚点B1和B2在线路两侧,因而21号道岔和23号道岔不能分在同一个道岔组中;由于5号、21号、19号、31号道岔没有同时满足以上2个条件,因而可以分在同一个道岔组中。同理可以得出25号、27号道岔不能分在同一个道岔组中。
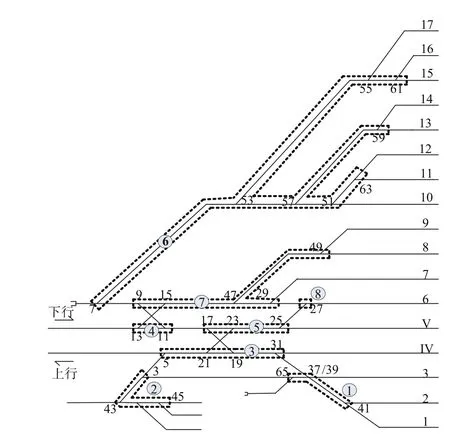
图 5 左端咽喉道岔分组Fig.5 Left throat turnout grouping
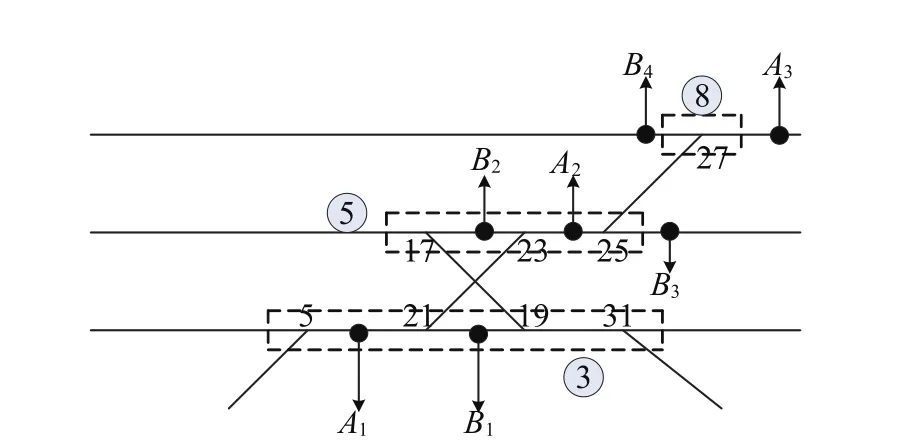
图6 坐标计算法Fig.6 Coordinate calculation method
同样以3号、5号、8号道岔组为例,用平行进路法验证如图7所示,3号道岔组在1道、2道、3道、IV道发车/调车进路中,5号道岔组在V道接车进路中,8号道岔组在6道调车进路中,因而3号、5号、8号道岔组分别在3条平行进路中,属于不同的道岔组,验证了这3个道岔组的分组正确性。
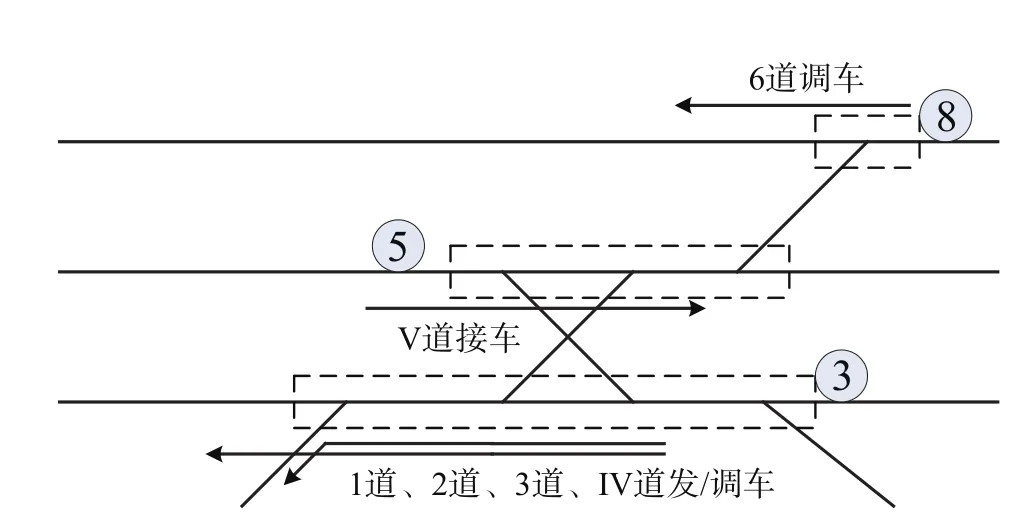
图 7 平行进路法Fig.7 Parallel routing method
3.2 2 种进路优化法在进路选择中的应用
3.2.1 2 种进路优化法在接发旅客列车过程中的 运用比较
(1)下行方向接旅客列车T303,1道、V道、6道均可接旅客列车,用最大平行进路优化法可得3条股道的最大平行作业数分别如下。①6道:4条(7道至17道的调车作业、IV道的发车作业、1道至3道的调车作业、经过5号道岔组的调车作业)。②V道:4条(6道至17道的调车作业、IV道的发车作业、1道至3道的调车作业、经过5号道岔组的调车作业)。③1道:2条(6道至17道的调车作业、经过5号道岔组的调车作业)。
因此,用最大平行进路法分析可得:旅客列车T303接到V道和6道的效果是一样的,但都优于1道,一般情况下,尽可能地将下行方向的旅客列车接到V道或6道,如果接到1道,这条接车进路将切割整个左端咽喉,给车站接发车作业和调车作业造成很大的干扰。
(2)用最大概率进路优化法可得剩余线路可以组成的后续进路数如下。①6道:25条(7道至17道的调车作业、1道至Ⅳ道的发车/调车作业、经过5号道岔组的调车作业)。②V道:26条(6道至17道的调车作业、1道至Ⅳ道的发车/调车作业、经过5号道岔组的调车作业)。③1道:15条(6道至17道的调车作业、经过5号道岔组的调车作业)。
因此,用最大概率进路法分析可得:旅客列车T303接到V道优于6道:在接发旅客列车作业过程当中,办理的都是基本进路,禁止办理迂回进路,因而6道进路只能经过4号、5号、8号道岔组,V道进路经过4号、5号道岔组,这样选择V道进路比6道进路多了1条6道调车进路。这2条进路明显优于1道进路。
从以上分析得出,在进路选择过程中,最大概率进路优化法比最大平行进路优化法能够更加准确地判断进路的优劣性[5]。
3.2.2 2 种进路优化法在接发旅客列车与超限列车中的运用比较
局管内旅客列车7507待避超限军列91007,7507可以接到1道、V道、6道,91007可以接到7道、8道、9道。
(1)用最大平行进路优化法分析旅客列车7507分别接到1道、V道、6道对超限军列91007接车进路数的影响。①1道:1条(7道/8道/9道接91007)。②V道:1条(7道/8道/9道接91007)。③6道:1条(8道/9道接91007,旅客列车与超限列车不能邻线接发)。因此,用最大平行进路优化法无法判断旅客列车7507接车进路对超限军列91007接车进路的影响。
(2)用最大概率进路优化法分析旅客列车7507分别接到1道、V道、6道对超限军列91007接车进路数的影响。①1道:3条(7道、8道、9道接91007)。②V道:3条(7道、8道、9道接91007)。③6道:2条(8道、9道接91007)。因此,用最大概率进路优化法可以判断旅客列车7507接到1道或V道优于6道,原因在于6道接旅客列车7507会影响7道接军列91007。
从以上分析得出,在进路选择过程中,最大概率进路优化法更加符合现场的实际作业情况。以上2种进路优化方法能够更加准确地指导现场作业,更加科学合理地选择列车进路,提高车站咽喉及整个车站的通过能力[9]。同时,车站咽喉通过能力的研究及进路优化的方法可为列车调度集中系统自动排路的优化提供理论依据。
4 结束语
以实际中间站为例,运用道岔分组原则对咽喉区复杂道岔进行简化,有效降低了咽喉区通过能力计算的复杂性,并且通过坐标计算法和平行进路法验证分组的正确性及可行性。在进路选择过程中,考虑了车站接发车作业和调车作业的综合因素,详细分析比较了不同情况下2种进路优化法的优劣性,有助于咽喉通过能力的研究。影响车站通过能力的因素有很多,不仅与现场各种设备有关,而且与现场作业人员的业务水平和经验也有很大关系。研究只简单考虑了接发车对后续接发车的影响,没有考虑所有股道的空闲或占用状态,默认了所有股道的空闲状态,而在实际作业过程当中,还存在着调车作业及各种相关因素的干扰,整个车站的作业更为复杂。因此,今后在此问题的研究过程中需要综合相关影响因素进行全面研究。
