不同P2P网络拓扑结构上进化博弈算法的研究
2018-08-10鲁春兰
鲁春兰
(西安航空职业技术学院电子工程学院,陕西西安710089)
Peer,中文意思为,伙伴,同事。由Peer组成的网络被称为对等网络,即Peer-to-Peer network[1]。P2P网络是建立在IP网络之上的应用层上的一种扁平化网络,其凭借良好的可扩展性、健壮性、通信匿名性、流量均衡、组网简单灵活等优势,应用极为广泛。P2P网络应用极为广泛,但仍然存在一些问题:“搭便车”现象[2]“洗白攻击”[3]“公共悲剧”[4]。国内外学者针对P2P网络的缺点,提出不同的模型来提升P2P网络中节点的合作性,比如:文献[5]将博弈论的观点引入对等网络中,文献[6]通过博弈论的方法研究了网络中节点的自私性,文献[7-9]研究了在不同激励下建立信任模型,文献[10]给P2P网络中的节点赋予一定信誉,节点根据其自身信誉享受不同的合作服务水平,文献[11-13]提出了在网格网络以及无标度网络中,节点间更易于形成合作稳态。
1 进化博弈算法描述
网络中的节点依次与自己的相邻节点进行囚徒困境博弈,博弈完成后,当前节点从邻居节点中选择收益值最高的节点策略作为自己的策略,这是一种进化型博弈模型。网络通过节点之间的动态演绎来激励合作状态的涌现。
文献[14]中已经证明网络节点被赋予一定的身份认证消息时,可以高效地遏制网络中的“搭便车”行为,提高节点之间的合作性。该算法在P2P网络里引入标兵节点,引导网络里的节点选择合作策略,另外,节点主动学习过程中根据收益差值选择邻居节点进行连接。通过仿真软件的仿真已经证实了该算法的有效性和可靠性。
本文在文献[14]的基础上,将进化博弈算法进行了优化,并在两种不同的P2P网络上进行了仿真,仿真结果证明,在不同结构的P2P网络中采取不同学习策略,网络中节点的合作性均有很大提高。
2 近似网格P2P网络上的进化博弈算法
为了抑制节点的自私性,Nowak等学者在网格网络上运用斑型图对囚徒困境展开了分析,发现网格网络里采取合作策略的节点在网络博弈过程汇总成簇,越聚越大,最后网络中会出现合作稳态[15]。除了规则网格网络外,还存在一种稀疏网格网络。稀疏网格中有节点的缺失,缺失的节点位置可以一直保持空白,也可以连接到网络中的其他节点上去。这样的组网方式与P2P网络形式十分类似,我们把这样的稀疏网格网络可以称作近似网格P2P网络。
本文的第一种进化博弈算法将在近似网格P2P网络上模拟,近似网格P2P网络由于其组网方式具有一定的规则性,其策略更新形式采用的选择最优收益进化式。
弱囚徒困境与经典囚徒困境的区别在于收益矩阵参数设置的不同。从文献[16]中可得出结论:弱囚徒困境与经典囚徒困境的演化结论是一致的。弱囚徒困境参数设置如下:R=1,T=1+r,P=S=0。其中,R<T=1+r<2R即0<r<1。r称为背叛诱惑因子。进化博弈双方的收益与收益矩阵有关,收益矩阵与背叛诱惑因子有关。因此,在计算节点收益,讨论网络中合作节点比例时必须从背叛诱惑因子入手。
3 改进型随机P2P网络上进化博弈算法
本文将构造一个类似无标度网络的改进型随机P2P网络,这个随机P2P网络也有优先连接特性。虽然新构造的改进型随机P2P网络里每个节点拥有的相邻节点数不一样,但可以计算改进型随机P2P网络里每一个节点的平均相邻的节点数,这个计算值是个固定的值。
改进型随机P2P网络中的每一个节点代表一个参与博弈的博弈者,节点之间的连线代表博弈者之间的信息交互。两个节点相互博弈,博弈活动完成后计算本次博弈的收益值。接着进行节点策略的更新,节点依次选择邻居节点计算策略转移概率p,接着系统产生一个随机数,如果该随机数的值小于策略转移概率p,则节点会将自己的策略更新为相邻节点的策略,策略更新过程完成。
改进型随机P2P网络由于其组网方式的随机性,为了平衡组网方式的随机性,在策略更新阶段采取了策略转移概率的更新方式。
策略转移概率p的计算公式如下:
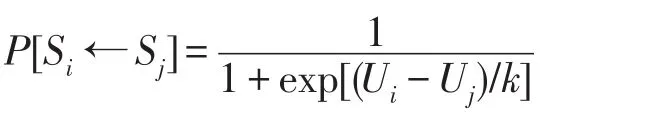
其中,Si,Sj分别表示节点i与节点j的策略,i表示当前节点,j表示相邻节点。
4 仿真结果及分析
4.1 近似网格P2P网络上的进化博弈算法参数配置
仿真实验是在N*N=200*200的稀疏网格网络上完成的。初始化网络中的合作节点为30%,不合作节点为70%,进化博弈算法运行100个周期。背叛诱惑因子的取值区间为0<r<1。
4.2 近似网格P2P网络上的进化博弈算法数据分析
实验中,令背叛因子的取值分别为r=0.05,0.25,0.45,0.65,0.85,讨论不同背叛因子对网络合作演化的作用。
图1中(a)~(e)图,分别表示的是当背叛因子r=0.05,0.25,0.45,0.65,0.85时,网络中合作节点与不合作节点的变化趋势。对比可知,r=0.85不适合充当背叛诱惑因子。
下面主要研究在近似网格P2P网络中,背叛诱惑因子的上限值。首先适当地减小背叛诱惑因子r的取值,定义r=0.8。图2表示背叛诱惑因子r=0.8时,合作节点与不合作节点所占比例变化趋势。从图中可以看出,不合作节点所占比例一直高于合作节点所占比例,网络在达到稳态之后,一直不会出现合作状态。因此,r=0.8不是所求背叛诱惑因子的上限。
实验中,又分别取了r=0.75,0.77,0.79来估算背叛诱惑因子的上限。图3、图4、图5分别表示r=0.75,0.77,0.79时,偏向合作态度的节点与选择不合作态度的节点所占比例变化趋势以及模拟过程中的动态演化过程图。
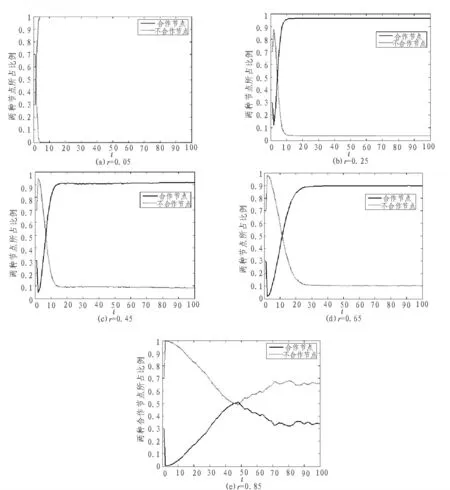
图1 不同背叛诱惑因子下,合作节点与不合作节点所占比例变化趋势
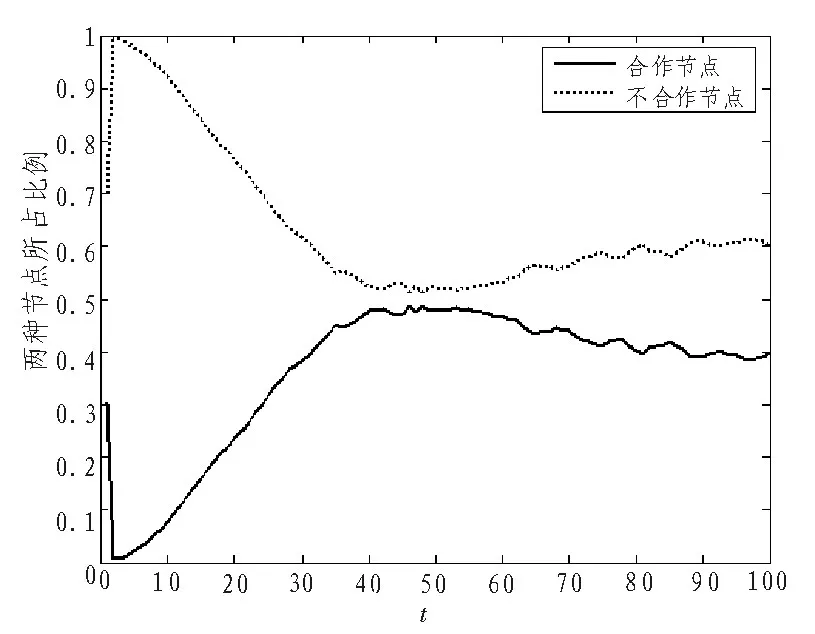
图2 背叛诱惑因子r=0.8时,合作节点与不合作节点所占比例变化趋势
对比这3组图,我们对出现合作稳态最快的图5进行分析。当背叛诱惑因子r=0.79时,从图5中(a)可以看出,模拟进行到第70周期时,网络就已经进入合作的稳定状态。网络在T0=42时,网络里有数量相等的两种节点。T=3时,合作节点处于变化曲线的波谷,对比动态演变过程,可以看到此时网络中不合作节点处于统治地位,随着模拟的不断进行,网络中出现了大量的合作节点形成的合作簇,逐渐扩展到不合作节点区域,最后整个网络处于合作稳定状态。
本文前面,通过模拟实验已经得出:背叛诱惑因子r=0.8不是所求背叛诱惑因子的上限。而当背叛诱惑因子r=0.79时,网络处于稳定的合作状态。因此,定性分析背叛诱惑因子r=0.79是背叛诱惑因子的上限。背叛诱惑因子的取值范围0<r<0.79。当背叛诱惑因子的值在本文所求解的取值范围内,近似网格P2P网络中就可以出现合作稳态。模拟证明,在近似网格P2P网络中采取策略更新择最优收益进化博弈算法可以使得网络中出现合作稳态。

图3 当背叛诱惑因子r=0.75时,图(a)表示合作节点与不合作节点所占比例变化趋势。图(b)~(f)分别表示的是模拟周期[T]为0、5、30、60、100时的动态演化过程。其中浅色表示不合作节点,深色表示合作节点。
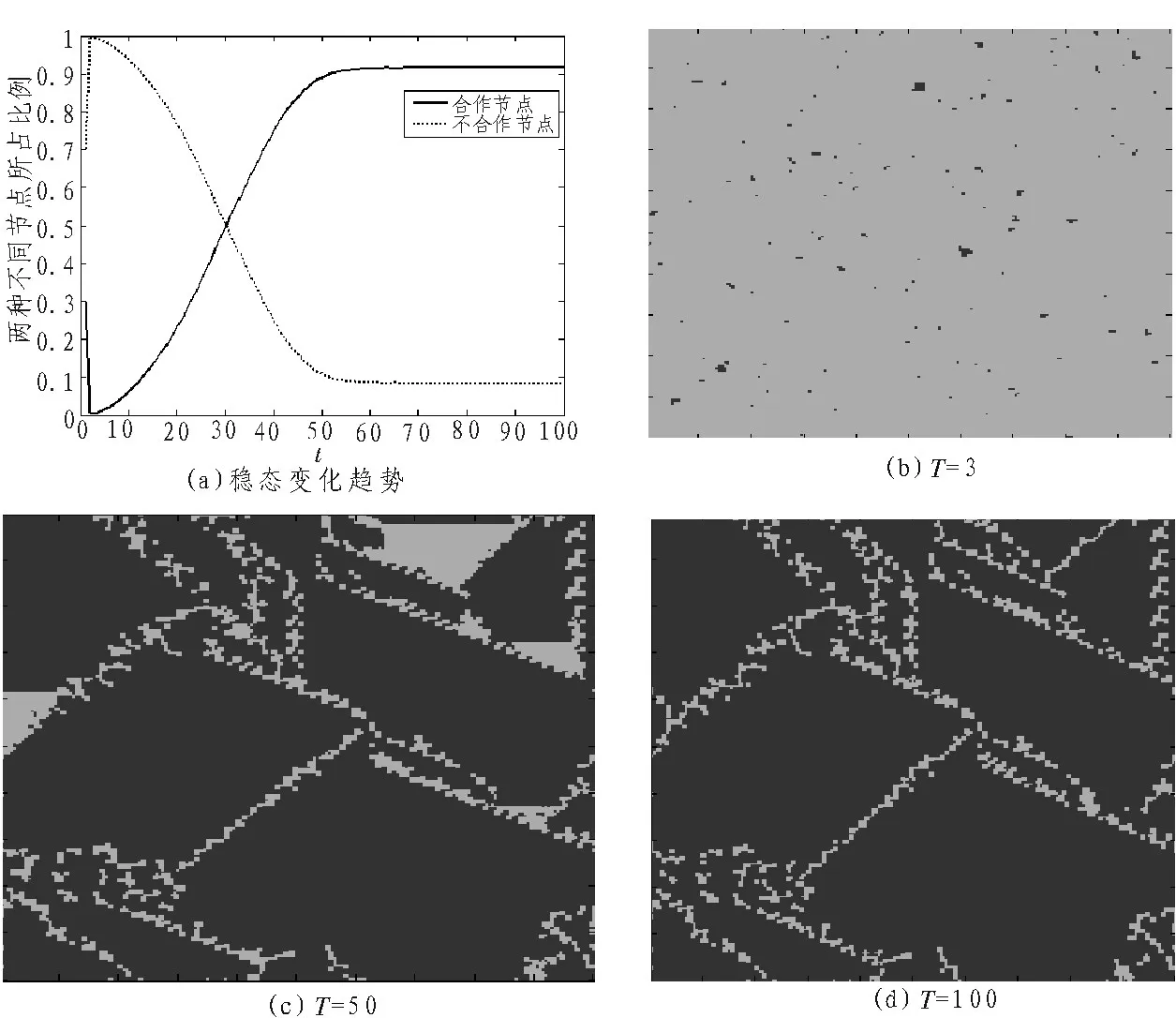
图4 当背叛诱惑因子r=0.77时,图(a)表示合作节点与不合作节点所占比例变化趋势。图(b)~(d)分别表示的是模拟周期T为3、50、100时的动态演化过程。其中浅色表示不合作节点,深色表示合作节点。
4.3 改进型随机P2P网络上进化博弈算法的研究
模拟实验运行的环境为改进型随机P2P网络,为了体现对节点策略的公平性,并促使网络中快速出现合作稳态,以下的实验将在初始合作节点为50%的环境中进行。
当设置背叛诱惑因子r的值为0.06时,网络中并未出现合作稳态。重新设置背叛诱惑因子的值,分别设置为0.99和0.1,初始化网络中合作节点为50%。实验运行100周期,结果如图6所示。

图5 当背叛诱惑因子r=0.79时,图(a)表示合作节点与不合作节点所占比例变化趋势。图(b)~(f)分别表示的是模拟周期T为3、50、70、80、100时的动态演化过程。其中浅色表示不合作节点,深色表示合作节点。
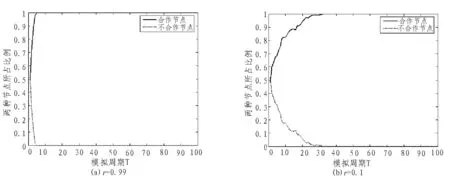
图6 初始化网络中合作节点为50%,图(a)是背叛诱惑因子r=0.99时,两种节点所占比例变化趋势,图(b)是背叛诱惑因子r=0.1时,两种节点所占比例变化趋势图。
当背叛诱惑因子为0.99和0.1时,模拟运行结束时两种状态的网络均达到了合作稳态。诱惑因子为0.99时,实验运行到第5周期网络已经达到了合作稳态,而r=0.1时的合作稳态则出现的稍微晚些,但也在第30周期出现合作稳态。由此可见,在随机P2P网络中,背叛诱惑因子越大,网络中出现合作稳态时间越短,网络越稳定。
接着,实验对背叛诱惑因子分别取值为0.07,0.065,0.063和0.061,模拟运行100周期,结果如图7所示。
由图7可以看出,这4种不同大小的背叛诱惑因子下,合作节点所占比例逐渐增长,网络中出现合作稳态。随着背叛诱惑因子的不断减小,合作稳态的稳固程度也依次减弱。
由于改进型随机P2P网络是一种完全随机的网络,节点之间博弈算法使用的收益矩阵是一种弱博弈矩阵,并且节点更新策略使用的是一种动态转移概率策略,该概率中加入了非理性选择的噪声,背叛诱惑因子越小,竞争因素相对也就越少,因此,这种网络情况下,网络中的合作稳态出现的较晚。相反,背叛诱惑因子越大,节点之间的竞争越激烈,节点更愿意选择合作策略,提高了网络中节点的整体收益,良好的整体收益更深入地促进了网络中合作稳态的出现。结合实验数据,得出背叛诱惑因子的取值范围为0.06<r<1时,改进型随机P2P网络中会出现合作稳态,并且背叛诱惑因子越大,合作稳态出现的越早越牢固。
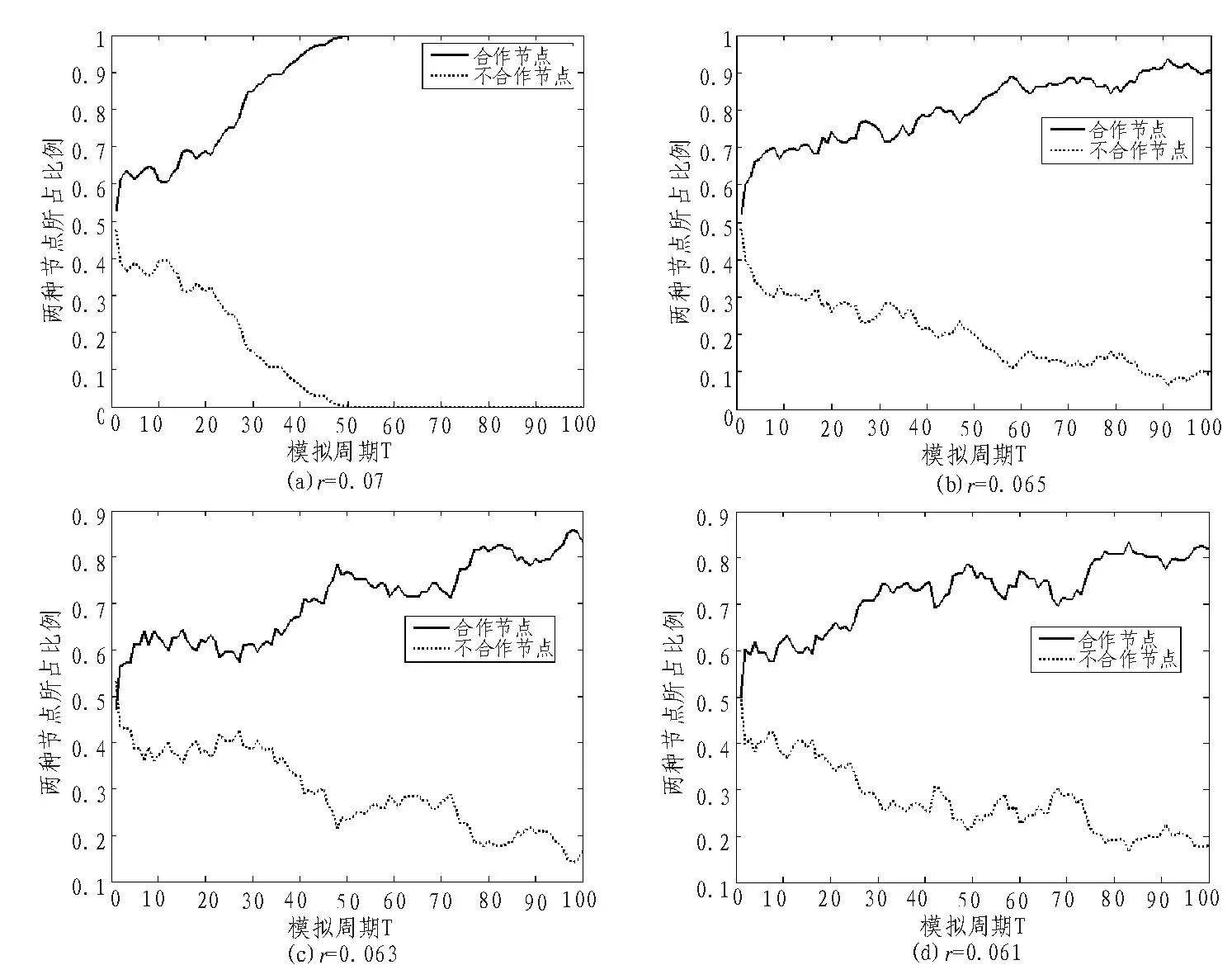
图7 图(a)~(d)分别是背叛诱惑因子为0.07,0.065,0.063,0.061时,网络中两种节点所占比例变化趋势
5 结束语
为了促进P2P网络中节点的合作性,本文分别在近似网格P2P网络中模拟了选择最优策略的进化博弈算法、在改进型P2P网络中模拟了选择概率转移策略的进化博弈算法。仿真结果证明,在这两种不同的拓扑结构中进化博弈算法均能促进网络中合作稳态的出现。
