一种手持式车身覆盖件的间隙测量系统

刘若晨 ，王庆宝 ，赵邦信 ，郭 磊

（1.南京理工大学电子工程与光电技术学院，江苏南京210094；2.易思维（天津）科技有限公司天津300380）

随着我国汽车行业在智能制造中的快速发展，在汽车生产中各个环节的检测测量显的越发重要。其中在汽车车身匹配环节中，车身外板覆盖件的间隙测量就是一个重要的评价手段。其测量精度将直接影响到车辆外观、车内封闭性、外部噪声大小与开关车门的效果。这些指标都将直接影响用户的驾车体验。目前，在绝大多数的汽车厂与零部件厂还是采用传统手工测量，例如塞尺，Cubing模型以及三坐标机等手段。这些都是通过接触式的方法进行测量，不仅无法实现零件匹配过程中对间隙的状态进行实时的测量，而且费时费力。因此如何利用先进的视觉检测与激光测量技术，客观地反映间隙的实际状态成为一个重要的课题。

间隙的测量精度与拍摄角度密切相关[1]。当传感器以一个角度进行拍摄时，对于间隙内部的信息常常会由于间隙表面的遮挡而无法获取，导致精度受损。因此需要多个视角的拍摄才可以测量。常用的方法为机器人携带传感器进行多角度拍摄或三维扫描的方法进行测量，其精度很高，在0.1 mm以内[2-3]。但针对传感器多个位置移动测量的坐标统一常常需要激光跟踪仪，V-STARS等高精度设备进行辅助测量。成本高，操作困难，标定复杂，使用局限等缺点使得该方法无法在工业现场进行大规模的推广。结构光系统的测量系统由于其精度高，造价低，柔性高等特点[4]经常被用在平面，棱线，凹槽等高精度测量上，其对宽度的检测优于0.3 mm[5]非常适合车身间隙的高精度测量。

针对以上问题，本文设计了一个手持式间隙测量系统，将两个线结构光系统融合到一起。从左右两边拍摄间隙，不仅可以有效避免由于视场遮挡导致的数据损失问题，而且加倍了点云密度提高了精度。此测量系统的一个难点就是系统的配准[6-7]，常用的双目配准方法是根据空间中相同点在不同图像中的坐标来实现其在三维空间中的配准。就加入线结构光的双目系统来说，其光条提取，光平面的标定误差将会导致两个相机获取的数据在三维空间中的配准精度下降[8-9]，因此往往还需再获取三维数据之后使用点云配准算法进行配准[10-12]。因此文中提出一种基于平面靶标的光平面与外参同时标定的方法，完成系统的配准，免去复杂的点云配准算法，满足手持式设备实时快速的测量要求。

1 双目线结构光测量系统模型

由于单目可能存在的视野盲区如图1所示。

图1 视野盲区图

本测量系统由两个相机两个线结构光构成，其相对位置关系如图2所示。

图2 系统结构图

其中两个激光器从左右两边照射间隙内部，可以获取其内部更多的信息。左边相机与左边激光器构成一个线结构光系统，右边同样可以构成一个线结构光系统。通过机械装置将两激光器的光平面调节重合后，两个相机从左右两边同时拍摄间隙位置，整体结构如图3所示。其中摄像机1坐标系为Oc1-Xc1Yc1Zc1，摄像机2坐标系为Oc2-Xc2Yc2Zc2激光条中心一点P在摄像机1坐标系下的位置坐标为P(Px1,Py1,Pz1)，根据理想的小孔成像模型可得：

图3 整体结构图

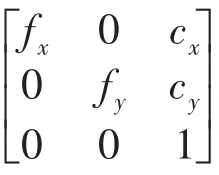
根据式（1）可得：

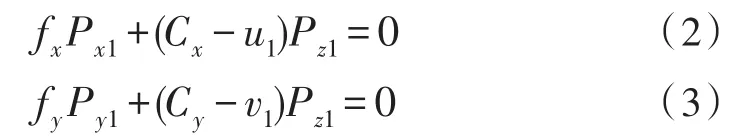
由于P点又在光平面上

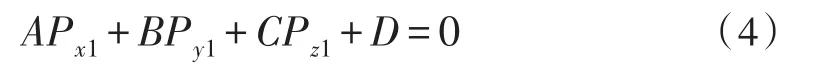
因此可以通过式（2）～（4）得出P点在摄像机1下的三维坐标：

因为两个摄像机均满足小孔成像理论，所以我们只需获取两个摄像机的内参与光平面参数即可求得光条上所有数据点在两个摄像机坐标系下的三维坐标。

此外如果这两个摄像机与两个激光器的相对位置不变，我们可以通过刚体变换将两个摄像机坐标系统一，即：

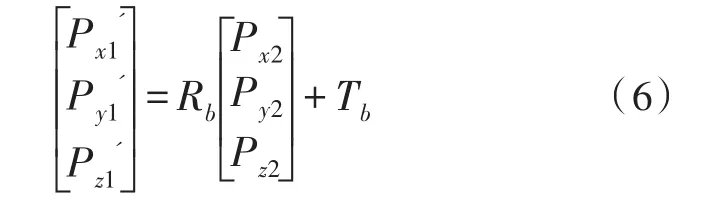
其中Rb，Tb为旋转矩阵和平移矩阵，就可以把摄像机2中点坐标统一到摄像机1中，进行计算。

2 测量系统参数标定

2.1 相机内参数标定

首先定义一个物体平面使得Z=0，使旋转矩阵减少一个列向量，根据式（1）～（5）可得图像点到空间点的射影关系：

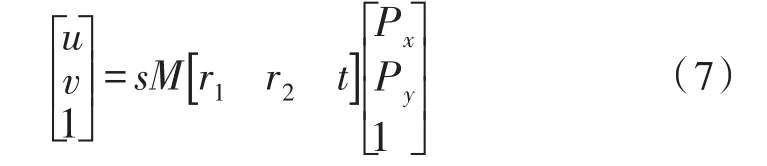
其中M为相机内参数矩阵，s为任意非零的尺度因子。设单应性矩阵H，即：

由射影矩阵与R满足正交特性（r1与r2的点积为0且向量长度相等），可得：

其中B=M-TM-1。

同时得到K个平面靶标图像，每幅图像都可以提供（9）、（10）两个约束条件，当K≥3时就可以从B矩阵中求得相机内参数的封闭解。

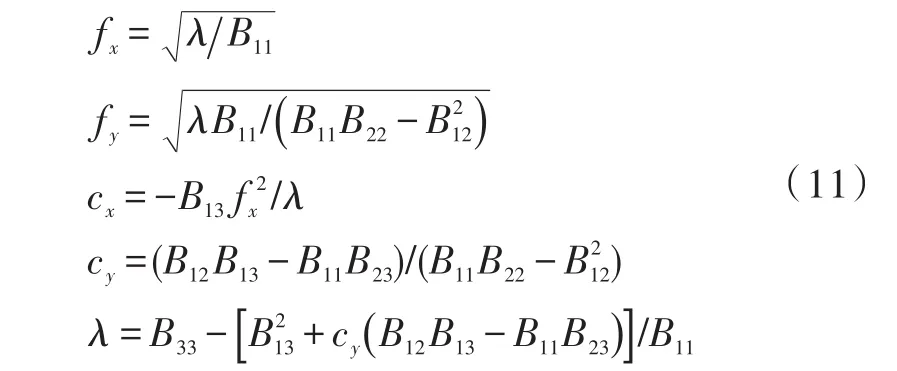
2.2 光平面标定

将激光条照射在一平面靶标上，假设平面上3个点Pb1～Pb3在世界坐标系下的坐标分别为(0 ,0,0)，(1,0,0)，(0,1,0)，则其在相机坐标系下的坐标可根据Pc1～3=RPb1～3+t求得，由 3点即可确定该的平面方程。因此只需知道该平面相对于摄像机坐标系下的外参再根据式（2）、（3）即可算出该激光条上点在相机坐标系下的三维坐标。再反推只需求得该平面的单应性H，即可通过已知的内参求解外参，即

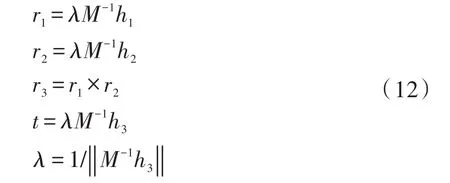
理论上超过两个位置的外参求解光平面。

2.3 相机之间转换关系标定

由于所有的点都在光平面上，因此可以在光平面上建立光平面坐标系，并利用刚体变换将摄像机坐标系上点转换到光平面坐标系中，可以有效的将三维数据转换为二维平面数据，简化计算。

由光平面Ax+By+Cz+D=0可得，设，TCP坐标系y轴的单位向量Rx可以基本认为和摄像机坐标系的x轴平行：

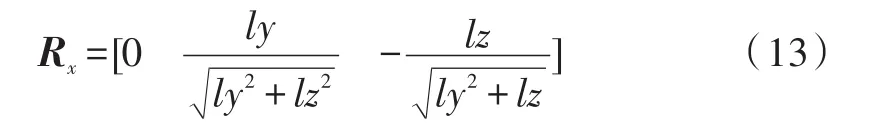
TCP坐标系z轴的单位向量Rz为光平面的法向量：

则TCP坐标系x轴的单位向量为：

因此摄像机坐标系与光平面坐标系旋转矩阵Rs与平移向量Ts为：

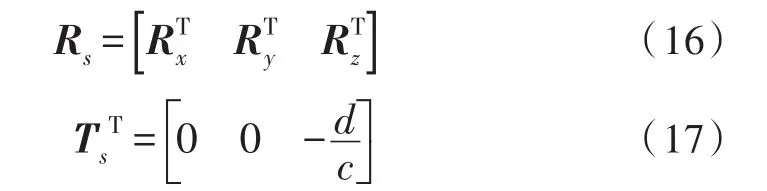
利用平面靶标的圆心构造直线，将该圆心直线与光平面相交，摄像机1与摄像机2同时采集图像。通过Hessian矩阵提取光条的亚像素中心。

分别对a、b求偏导整理并求解方程可由此将光平面图像坐标拟合直线求解该直线与靶标圆心构造出直线的交点坐标。

通过摄像机1与摄像机2拍摄的交点坐标，通过式（5）求得该交点的在两相机坐标系三维坐标pi,qi。根据空间刚体变换模型构建方程：

其中ωi代表每个点的权重，这里设为1。将R看作不变量对t进行求导，可得：

3 尺寸计算

车身覆盖件上间隙检测位置如图4所示。线结构光条中心提取是激光三角测量的重要环节[13-14]。首先通过Hessian矩阵提取光条中心[15]，因此首先通过图像分割找出间隙位置，仅对光条弯曲部分进行卷积，其余直线部分采用灰度质心法计算即可。考虑到间隙内部信息可能为椭圆。使用Ramer多边形逼近算法[16]时的目标函数改为椭圆函数。

图4 间隙测量图

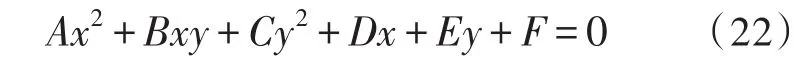
如果其拟合误差小于直线拟合误差，则认为是椭圆，即：

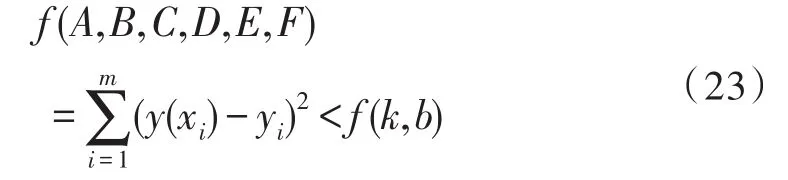
因此可以得到4个拐点p1～p4，拟合两椭圆心a，b之间的方向即为测量方向，减去相应的椭圆半径即为间隙测量值d。

4 实验及讨论

实验采用ar134相机与7.4 mm焦距的镜头。工作距离为80 mm，以相机1为全局坐标系。首先拍摄光刻靶标对相机内参数进行标定，然后通过前后移动3个不同位置拍摄平面靶标对光平面与相机2到相机1的转换关系（即系统外参数）进行标定，如图5所示。

图5 标定实验图场景图

图6 标定板图片

通过这10张靶标图像建立摄像机内参优化校准函数。

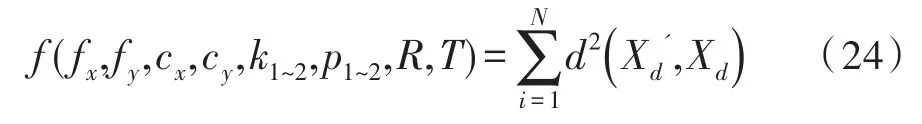
其中d(Xd',Xd)为计算投影点到实际投影点的距离。实验计算出的反投影误差为0.03 mm，光平面拟合误差为0.02 mm，均可以满足该测量需求。实验测量的间隙测量值是1.4 mm为塞尺测量，精度为0.02 mm。

5 误差分析

由于两激光器为机械调整重合，并不能保证两激光器发出的光平面完全重合。因此将被测物体前后移动，不在工作距离的时候，激光图案变粗，但并不满足高斯分布，而是出现不同程度的上下偏移如图7所示，这和激光器出瞳的角度也有一定得关系，因此需要利用相机1图像中的直线段，求解相机2图像中直线段的点到其平均距离作为修正矩阵，完成点云配准如图8（c）所示。

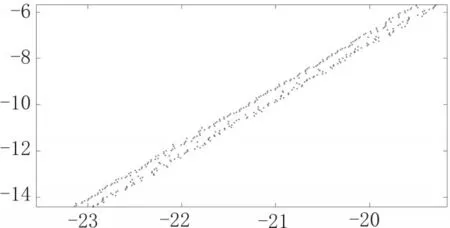
图7 配准前的二维坐标

图8 配准前、后和修正后的图像

在点云配准中，我们使用最临近点间距的平方和来评价点云配准的精度，任取10个位置修正效果如表1。

其中误差较大是由于两个相机视场并非完全重合导致，就左右相机对应点之间的欧式距离如图9，可以看出点云对齐后平均距离为0.03 mm左右。

因为拍摄间隙图片时不能保证一定垂直与间隙表面，因此在不同角度下拍摄间隙图片，如表2。实验结果表明可以在45°角的拍摄范围内平均误差小于0.1 mm。

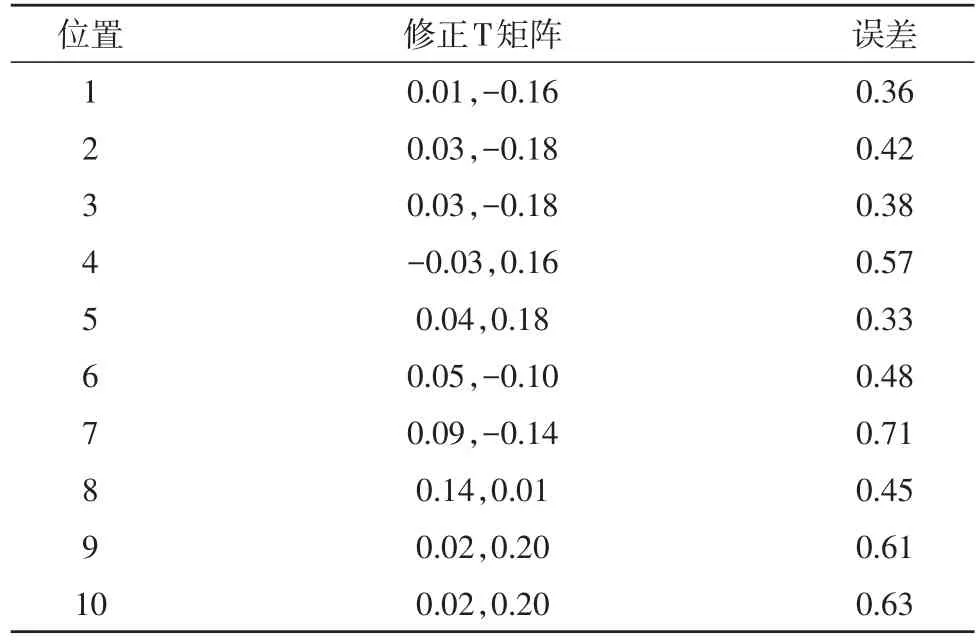
表1 使用修正矩阵后修正效果

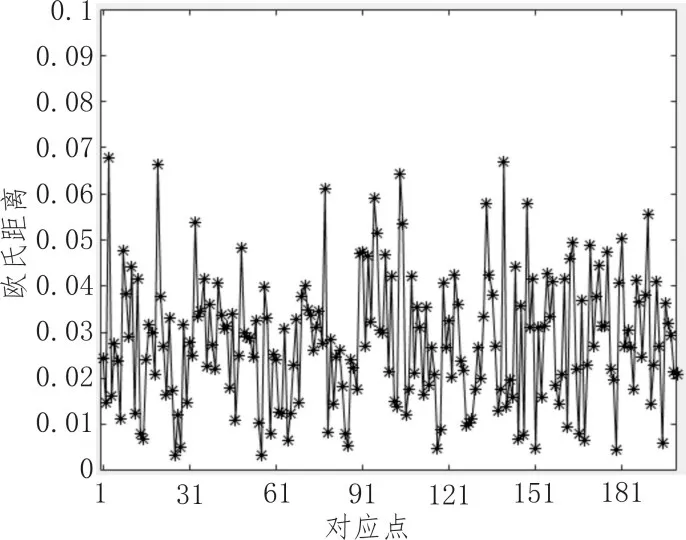
图9 对应点之间的欧式距离

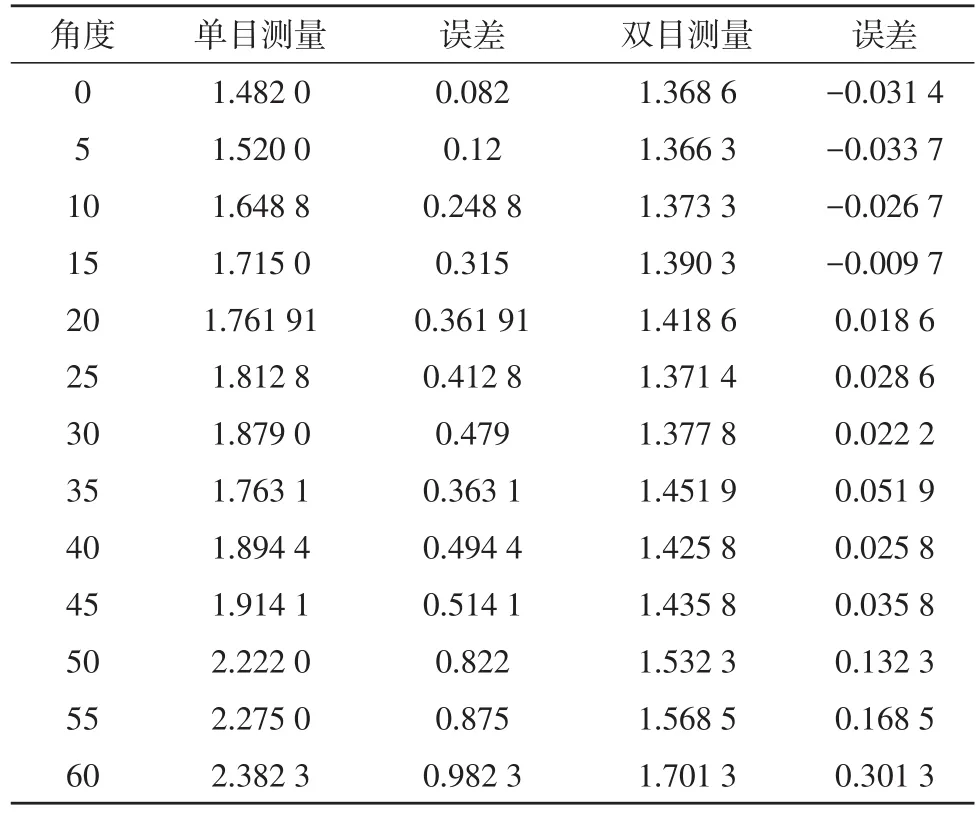
表2 不同角度下的测量结果

6 结论

本文根据车身覆盖件间隙的高精度、高鲁棒性测量要求，提出一种双目线结构光测量系统。并介绍了该系统的工作原理，通过图像一体化标定相机内外参数，构建TCP坐标系将三维数据转换为二维不仅降低了计算的复杂性还可以通过靶标中心与激光条交点精确求解两相机坐标系间的转换关系。并给出了由于激光器机械调整误差的修正方法。最终完成了间隙测量。该系统在不同位置不同角度下进行测量，在45°拍摄角度以内测量精度达到0.1 mm，鲁棒性好。在未来的工作中，将曲率，棱线，平面度，高度差等算法集成进来，可以使得车间工人仅需手握此测量设备便可进行多种测量，另外制作小型化的手持式的检测系统也是未来发展方向之一。