基于VB的数学测量坐标系统转换程序设计与实现研究
2018-08-10杜满良
杜满良
(咸阳师范学院陕西咸阳712000)
因为多种因素,在测绘生产过程中所使用的坐标系统比较多,为了能够有效满足不同部门用图的需求,并且实现不同坐标系统数据之间的共享,就要实现旧坐标系成果的转换,使其能够成为全新的坐标系成果。传统使用测绘成果资料中的坐标系都是北京坐标系或者西安坐标系,在国家大地坐标系不断推广使用的过程中,要求将所有的测绘成果都转换成为国家大地坐标系。并且,为了能够便于测绘成果的管理及使用,在工程建设过程中使用的地方独立坐标系及国家坐标系能够互相的转换。所以,为了能够对坐标系统转换程序进行开发,就要实现不同坐标的相互转换,以此能够对现实测量过程中的问题进行解决。本文使用VB实现数学测量坐标系统的转换,使用户能够方便并且简单的实现不同坐标系统坐标的转换。
1 转换数学模型
一般现代使用的坐标转换具有七参数转换和四参数转换。四参数转换是一种二维转换方式,其要利用高斯投影才能够得到平面坐标,之后对转换参数进行计算。七参数转换主要包括武测模型、莫洛金斯基模型及布尔莎模型等,其是一种三维坐标转换。布尔莎模型是将原来的坐标系原点作为重点,实现坐标的缩放、旋转及评议变换;武测模型是将原来的坐标系原点作为中心,实现坐标的平移、旋转,将测区的参考点作为中心实现缩放。莫洛金斯基模型是将测区范围将某个参考点作为变换中心实现坐标的缩放及旋转,将原来坐标的原点作为中心实现评议变换[1]。
1.1 布尔莎模型
布尔莎模型中具有7个参数,包括3个平移参数和3个旋转参数、一个尺度参数,因为坐标系统在转换过程中的旋转角都是极小的角度,其简化模型为:

1.2 平面四参数模型
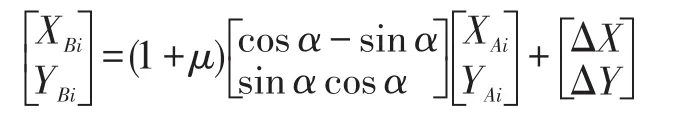
1.3 莫洛金斯基模型
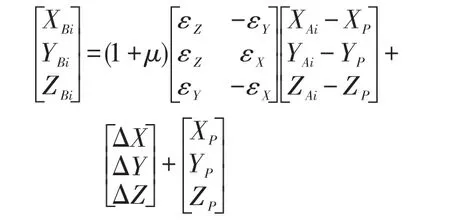
1.4 选择转换模型
平面四参数转换只是在小区域和不同定义中的两个坐标系转换中使用,其属于工程应用中最多并且直观、简单的数学模型。七参数转换从理论方面分析较为严密,其将所有所坐标系的定位定向差异进行了全面的考虑,保证只使用两种坐标系的严密转换,其适应于大型的项目坐标转换中,在实际使用过程中,要全面考虑待转换坐标系的信息、区域的大小、公共点分布及数量等多种情况,从而选择最优的坐标转换模型[2-3]。
2 系统的功能设计
文中所设计的数字测量坐标系统转换程序主要使用模块化实现,图1为基于VB的数学测量坐标系统转换的功能结构。
系统中的参数设置模块主要包括四参数、参考椭球及七参数设置。不同坐标系在不同参考椭球之间转换的时候,其偏心率和半径等多种参数都不同,系统具有北京54坐标系、80坐标系等参考椭球参数的设置,四参数的设置能够在各种高斯平面中相互转换。七参数转换是在不同空间直角坐标系转换中使用,用户能够根据自己的实际情况实现设置[4-5]。

图1 基于VB的数学测量坐标系统转换的功能结构
2.1 转换方式
转换方式模块主要指的是坐标转换使用单点转换方式或者文件转换方式,如果属于单点转换,那么用户就要在界面中将原来的坐标进行输入之后点击转换按钮,然后在另外文本框中得到转换之后坐标。
简单来说,文件转换就是在转换前后参数及数据的文件化管理,用户能够将一种转换作为另外文件进行保存,在下次使用之后通过文件菜单选择打开此文件对已经有的转换参数进行调用,还能够选择自己想要设置的文件格式[6-7]。
2.2 坐标转换
系统中的坐标转换模块主要包括不同的平面直角坐标系转换、不同的大地坐标转换、空间直角坐标系对大地坐标的转换、不同坐标投影带及不同高斯平面直角坐标系的转换。
1)高斯平面直角对平面直角坐标转换。基于参考的椭球及坐标转换前后不变,在椭球出现变化的之后,要根据不同参考椭球及四参数转换两者的参数实现坐标的相互转换[8]。
2)高斯平面直角坐标朝着空间指标坐标系转换。在椭球不发生变化的时候,要使大地坐标朝着空间直角坐标进行转换。如果参考椭球出现变化,那么就要将平面直角坐标转换成为大地坐标,之后再转换成为空间指标坐标,以参考椭球及七参数转换两者的参数为基础,将空间直角坐标朝着目标参考椭球中的空间直角坐标进行转换[9]。
3)高斯平面直角坐标朝着大地坐标转换。在参考椭球不发生变化的时候,能够通过高斯坐标反算公式实现转换。如果参考椭球出现变化的时候,要以不同参考椭球及四参数为基础,将高斯平面直角坐标转换成为目标参考椭球中的平面直角坐标,之后通过高斯反算公式使其成为目标椭球中的大地坐标[10]。
2.3 坐标换带模块
此模块首先要对参数进行设置,比如中央子午线经度、换带前后基准纬度、换带类型、参考椭球等。之后将原来的坐标通过高斯坐标反算函数转换成为大地坐标,之后通过大地坐标纬度、全新中央子午线经度及经度和,通过坐标正算函数计算全新投影中的坐标,并且要对坐标是否为自然值和通用值进行全面的考虑[11]。
3 系统界面设计
系统以克拉索夫斯基椭球体实现平面坐标朝着大地坐标进行转换,在实现批量数据的处理,计算批量导入的数据,并且还能够实现批量的输出。单点数据及批量数据的反算具有较高且稳定的精度,并且还具有较高的可靠性[12],图2~图5为系统的处理界面。
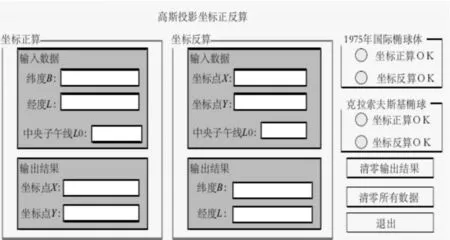
图2 单点正反算界面
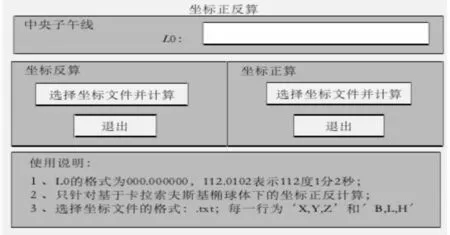
图3 批量坐标正方算界面
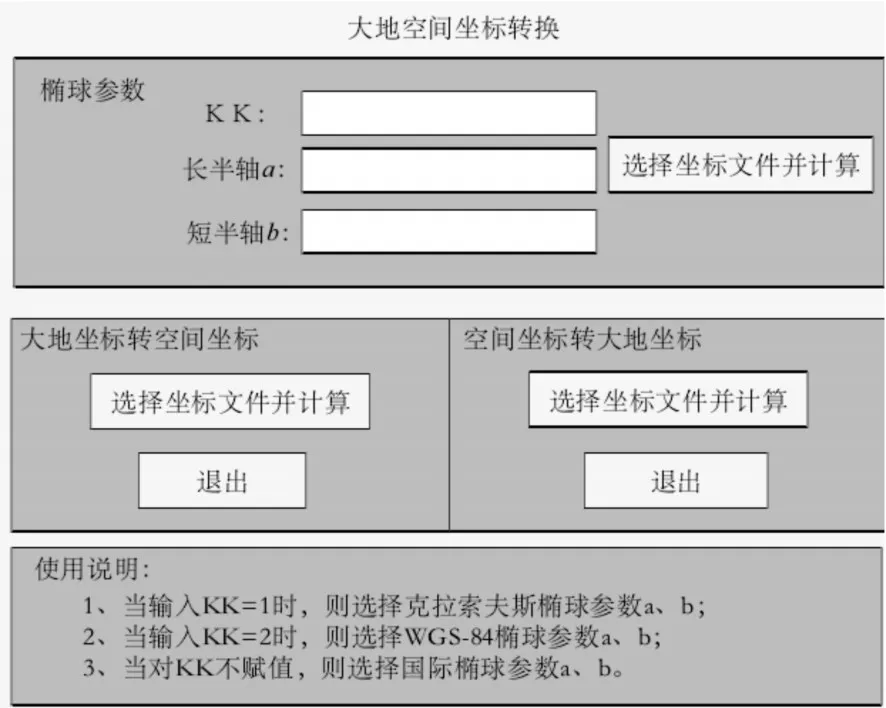
图4 大地空间坐标转换界面
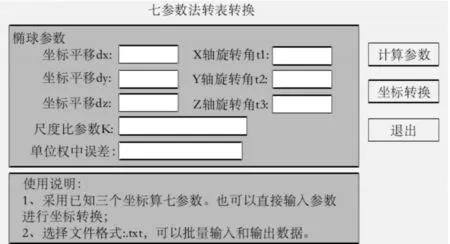
图5 坐标转换界面
系统的转换流程主要为:
1)准备数据。需要提供测试区域中原来坐标系和目标坐标系的公共点坐标,选择具有较高精度,并且分布较为合理,能够对整个测区都覆盖的公共点有效实现参数的计算。如果为七参数转换,那么就要具备大地高和经纬度。如果为四参数转换,就要具备平面直角坐标。通过Excel表的形式实现编辑和保存,需要坐标转换的数据要使用TXT文本文件的编辑模式进行保存[13]。
2)投影参数的设置,主要包括Y坐标加常数、中央子午线精度、投影高程。
3)对原来坐标系及目标坐标系进行全面的设置,对椭球基准进行选择,实现转换模型的确定。
4)对转换参数计算公共点的坐标进行读取,对转换参数进行计算。
5)通过参数计算公共点对内符合精度进行计算,通过没有参与转换参数计算的公共点外符合进度进行计算,对在坐标转换参数粗差公共点进行查找和剔除,使用可靠的公共点进行计算并且实现坐标转换参数的计算,直到进度能够有效满足限差。
6)对坐标转换的数据进行读取,根据转换的参数对坐标转换进行执行,并且得到全部需要转换点转换的坐标[14]。
4 基于VB的坐标转换部分类及结构体
4.1 坐标系统结构体的定义
首先要实现不同坐标系结构体的定义:


4.2 坐标转换类
以坐标转换类型为基础实现坐标转换类的定义:

5 系统的测试
选择某个矿区分布较为均匀,并且具有较高坐标精度,而且在整个矿区进行覆盖的5个公共点对转换参数进行计算,选择8个没有参与到转换参数计算中的公共点,将其作为外部检核点,通过2016年矿区大地水准面精化成果中的插高程异常值,分别使用平面四参数模型、莫洛金斯基模型及布尔莎模型实现北京坐标系到大地坐标系和西安坐标系到大地坐标系的相互转换[15]。详细数据见表1~表3。

表1 平面四参数模型比较表
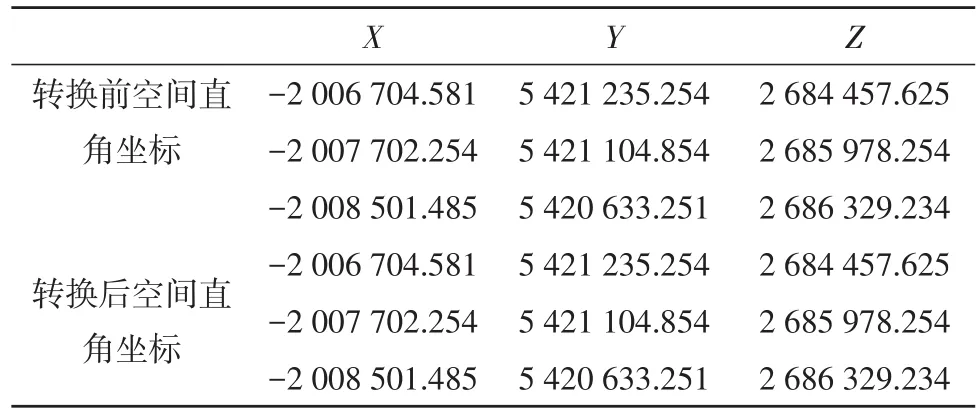
表2 莫洛金斯基模型比较表
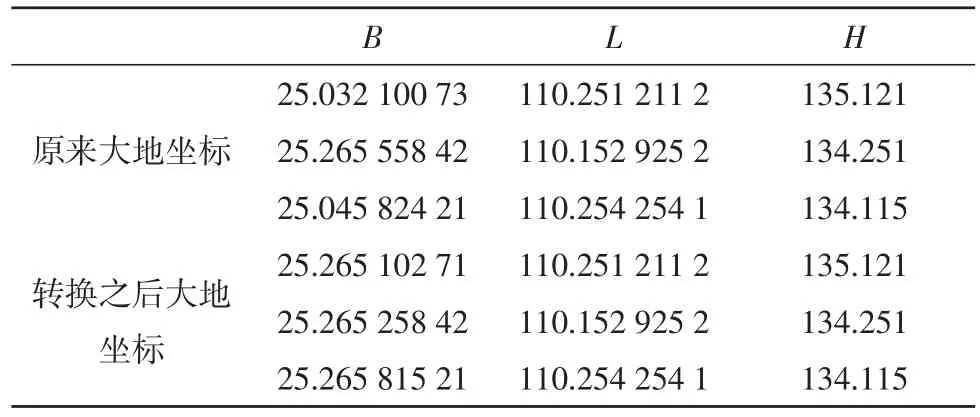
表3 布尔莎模型比较表
通过分析表示:
1)因为北京坐标系坐标是通过局部分区平差计算,西安坐标系坐标是通过整体平差实现,所以北京坐标系坐标没有良好的内符合性,并且其中的内符合及外符合的精度都比较低,并且程序在运行过程中对这点进行了验证。
2)此矿区通过本文所设计的测量坐标系统转换程序在实现坐标系统转换过程中点位中的误差在5 cm之间,满足国家相应的规定标准。通过程序能够实现所有范围中坐标系的快速转换,如果具有较高的公共点进度并且范围的分布比较合理,其转换的误差更小,能够有效满足测绘及生产的需求。
3)本文设计的程序通过验证其运行比较稳定,并且运行的速度比较快,计算出来的结果比较可靠[16]。
6 结束语
文中根据不同及相同参考椭球坐标系的转换原理通过VB语言定义相关结构体和不同类能够满足不同参考椭球情况中的计算,并且利用某矿山实际的案例进行了检验,表示本文所设计的系统程序可靠,能够满足实际的精度需求。
