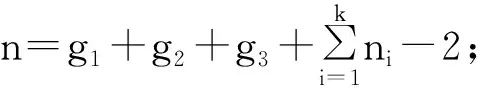具有k个悬挂点的一类特殊三圈图的Harary指数

景 芬，邵燕灵

(中北大学 理学院， 太原 030051)

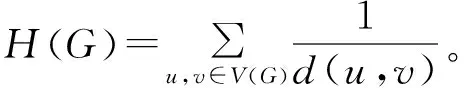
本文研究的特殊三圈图是指具有k个悬挂点且三圈只有1个公共顶点的图。同时给出此类图中有极大Harary指数的极图的图类。

1 引理

以下先给出几条证明定理所需要的引理。

引理1[7]设G是阶数n≥2的连通图，u是G的顶点。设Gk,l是G在u处添加两条长为k和l的路P和Q后得到的图，其中P：uv1v2…vk，Q：uu1u2…ul，v1,v2,…,vk和u1,u2,…,ul是不同的点，若k≥l≥1，则H(Gk,l)>H(Gk+1,l-1)。

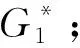
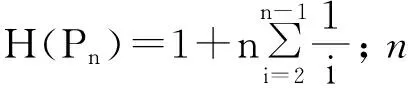
2 主要结论

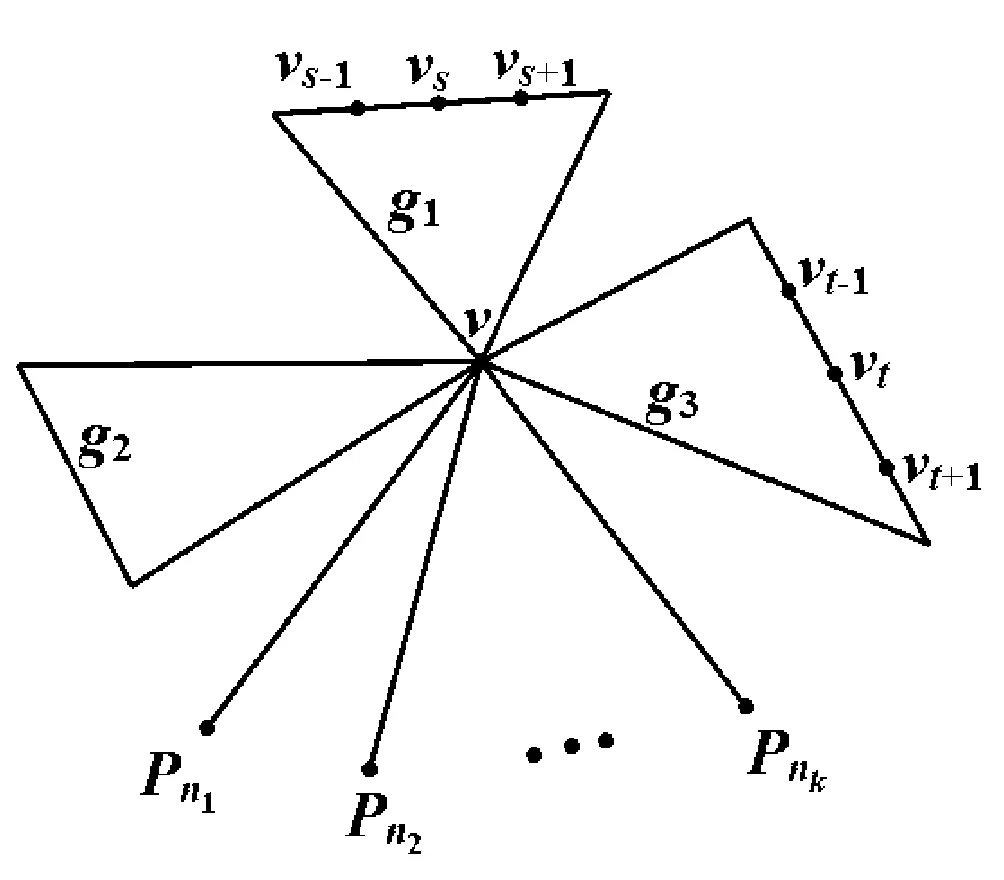
设Un,k是所有恰含k个悬挂点且3个圈有且仅有1个公共顶点的n阶三圈图的集合。设Un,k(g1,g2,g3)⊆Un,k是3个圈(记为Cg1,Cg2,Cg3)的长度分别为g1、g2、g3的Un,k中图的集合。

引理4 设G∈Un,k(g1,g2,g3)是Un,k(g1,g2,g3)中Harary指数极大图，点v是G中3个圈的公共顶点，则G中所有圈上顶点(除点v外)的度至多为2。

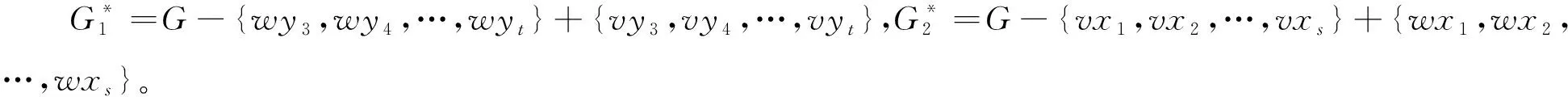
引理5 设G∈Un,k(g1,g2,g3)是Un,k(g1,g2,g3)中Harary指数极大的图，点v是G中3个圈的公共顶点，则点v是G中唯一的度大于2的点。

证明由引理4，G中所有圈上顶点(除点v外)的度至多为2。下面仅需证明G中所有不在圈上的点的度至多为2。

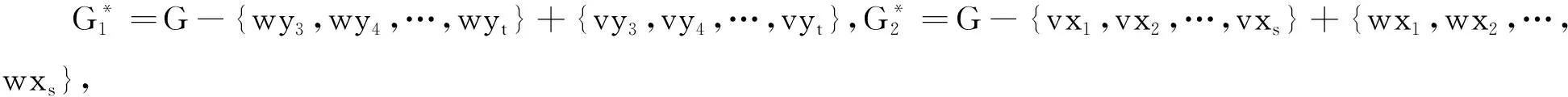
图1 Un,k(g1,g2,g3)中的图

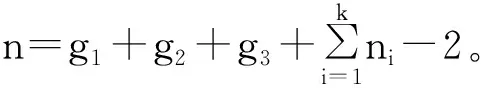
引理6 设G∈Un,k(g1,g2,g3)是Un,k(g1,g2,g3)中Harary指数极大的图，则G≅Un,k(g1,g2,g3,n1,n2,…,nk)，且|ni-nj|≤1，1≤i,j≤k。

证明设G∈Un,k(g1,g2,g3)是Un,k中Harary指数极大的图，由引理4与引理5可知，G≅Un,k(g1,g2,g3,n1,n2,…,nk)。此时，由引理4不难看出，对任意1≤i,j≤k，有|ni-nj|≤1。证明完毕。

引理7 设G∈Un,k(g1,g2,g3)是Un,k(g1,g2,g3)中Harary指数极大的图，则G≅Un,k(g1,g2,g3,n1,n2,…,nk)，其中|gi-gj|≤1，1≤i,j≤3。

证明设G∈Un,k(g1,g2,g3)是Un,k中Harary指数极大的图，由引理6知，G≅Un,k(g1,g2,g3,n1,n2,…,nk)，且|ni-nj|≤1，1≤i,j≤k。下面用反证法证明对任意1≤i,j≤3，|gi-gj|≤1。

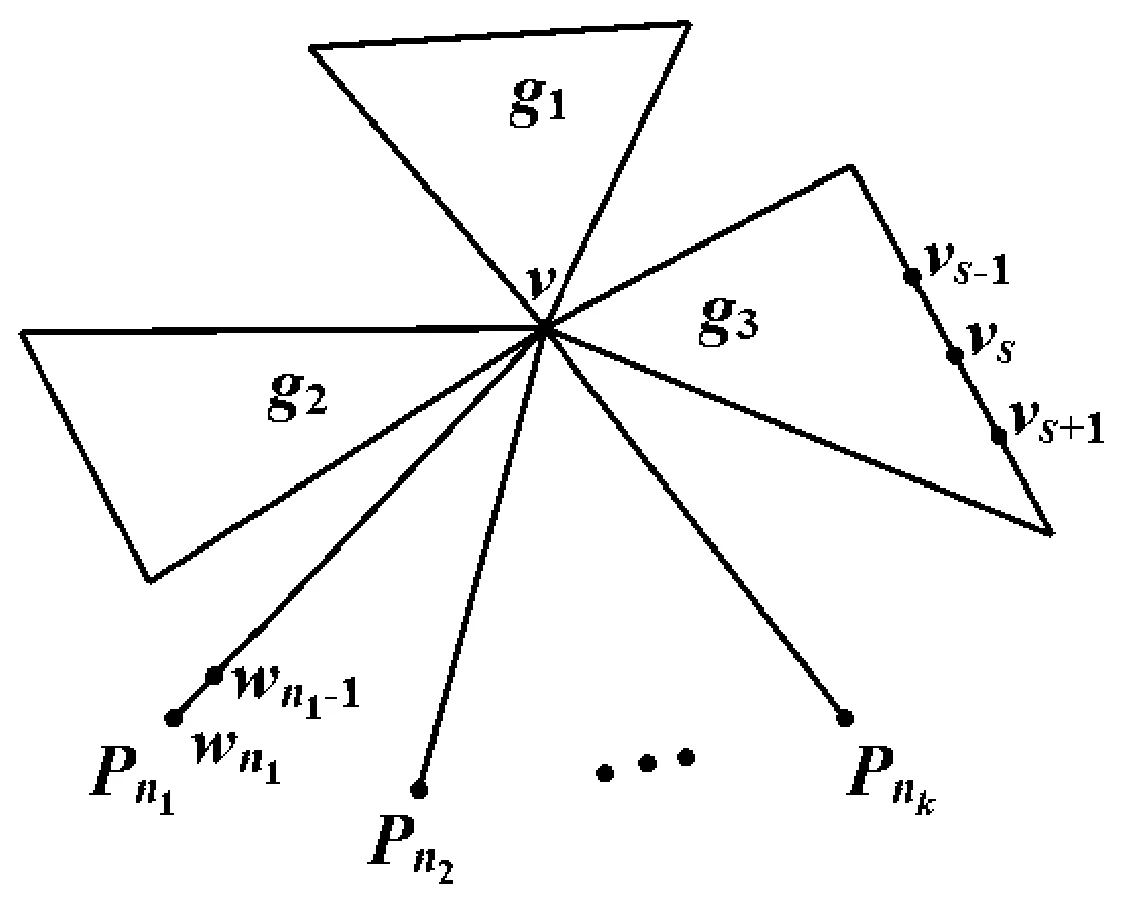
不妨设g1≥g2≥g3，且g1-g3≥2。令Cg1=vv1v2…vg1v，Cg3=vu1u2…ug3v，G′=G-{v1v2,vu1}+{vv2,v1u1}，如图3、4所示。下面将分4种情形证明H(G)

图3 Un,k(g1,g2,g3)中Harary指数极大图

情形1g1与g3均为偶数，则

① 当g1-g3=2时，

② 当g1-g3>2时，

情形2g1为偶数，而g3为奇数，则

情形3g1为奇数，而g3为偶数，则

情形4g1与g3均为奇数，则

① 当g1-g3=2时，

② 当g1-g3>2时，

综合上述4种情形知H(G)

引理8 设G∈Un,k(g1,g2,g3)是Un,k中Harary指数极大的图，则G≅Un,k(g1,g2,g3,n1,n2,…,nk)，且min{g1,g2,g3}>2max{n1,n2,…,nk}。

证明首先由引理6与引理7知，G≅Un,k(g1,g2,g3,n1,n2,…,nk)，对任意1≤i,j≤k有|ni-nj|≤1，且对任意1≤i,j≤3有|gi-gj|≤1。不妨设g1≥g2≥g3，n1≥n2≥…≥nk。

若g1≤2n1，考虑图G′=G-{wn1wn1-1,vtvt+1}+{vtwn1,wn1vt+1}，如图5、6所示，下面将证明H(G)≤H(G′)。

图5 Un,k(g1,g2,g3)中Harary指数极大图

图6 G′=G-{wn1wn1-1,vtvt+1}+{vtwn1,wn1vt+1}

情形1g1=g2=g3。

① 若g1=g2=g3为偶数，则

② 若g1=g2=g3为奇数，此时g3≤2n1-1，从而

情形2g1=g2，g3=g2-1。

① 若g3为偶数，而g2为奇数，则

② 若g3为奇数，而g2为偶数，则

情形3g2=g3=g1-1。

① 若g1为奇数，而g3为偶数，则

② 若g1为偶数，g3为奇数，则

从上述3种情形的讨论知，若g1≤2n1，则H(G)≤H(G′)，这与H(G)的极大性矛盾。证明完毕。

综合引理4～8，得到关于Un,k中具有极大Harary指数的图的特征刻画如下：

定理9 设G∈Un,k(g1,g2,g3)是Un,k中Harary指数极大的图，则G∈Un,k(g1,g2,g3,n1,n2,…,nk)，且满足

② |ni-nj|≤1，1≤i,j≤k；

③ |gi-gj|≤1，1≤i,j≤k；

④ min{g1,g2,g3}>2max{n1,n2,…,nk}。