一道双变量问题的三种解法及应用

孙 健

（鞍山市第一中学数学组，辽宁 鞍山）

在解决函数导数部分的问题时，我们经常遇到双变量的问题，由于两个变量都在变动，学生经常在解题时束手无策。因此笔者从一道题典型的双变量问题切入，给出双变量问题的三个不同的解题方法，希望能对同学们有所启发。

法一：分离变量

考虑函数g（x）=x0lnx-x，则g（x1）=g（x2）

若x1＜x2≤x0，而g（x）在（-∞，x0］单调递增，g（x1）＜g（x2）与g（x1）=g（x2）矛盾，

同理x0≤x1＜x2亦与g（x1）=g（x2）矛盾

所以x1＜x0＜x2

说明：此法利用已知条件关于x1，x2两个变量对称形式，将两个变量分离到等式两侧，进而将已知条件转化为g（x）在x1，x2处的函数值相等，并通过研究g（x）性质找到x1，x0，x2之间的大小关系。

法二：用变量组合式做变量

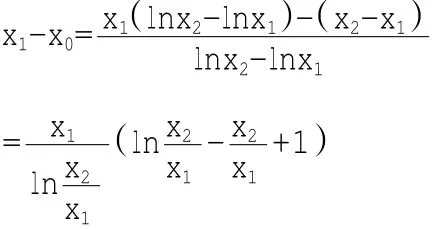
考虑函数g（t）=lnt-t+1

类似可证x2-x0＞0

说明：比较两数大小关系时做差和做商是常见的方法，此方法直接做差，并找到做差后式子中符号固定的部分后重点考虑不易确定符号的部分，通过对数的运算法，则巧妙地将两个变量的商作为新的变量构造出一个单变量的函数。此法也可以利用做商的方式处理，这里留给读者思考，不再赘述。

法三：一个看做自变量，一个看做常数

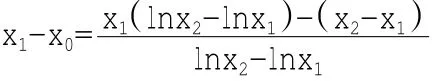
考虑函数g（x）=x1（lnx-lnx1）-（x-x1）

而x1＜x2，故g（x2）=x1（lnx2-lnx1）-（x2-x1）＜g（x1）=0

说明：此方法做差的想法与法二类似，不同的是在处理分子时将x2作为自变量，将x1看做常数构造出函数g（x），这种处理方法源自数学分析中多元微积分中的偏导数方法,以大学观点处理高中导数题目自有欲穷千里目，更上一层楼的感觉。

以上三种解法是双变量问题中较为典型的处理技巧，下面我们对以上方法加以应用，并体会对不同类型的题目如何选取适当的方法。

应用：

（1）已知f（x）满足f（x）+f′（x）＞0，∀x∈R，比较f（2）与大小。

解：f（2）与大小关系等价于e2·f（2）与f（0）大小关系，而利用函数单调性比较大小是一种常规方法，若可以将两式转变为同一个函数在不同点处函数值则问题可解。注意到e2·f（2）与f（0）两式在形式上相差函数符号f前面的一个常数e0，e2·f（2）与f（0）大小关系等价于e2·f（2）与e0·f（0）大小关系，两式分别为g（2）与g（0）。

考虑，g（x）=ex·f（x），g′（x）=ex·（f（x）+f′（x））＞0，g（x）单调递增，故

（2）已知函数f（x）=（a+1）lnx+ax2+1

设a≤-2证明：对任意

解：不妨设x2≤x1，则或f（x1）-f（x2）≤4（x2-x1）

⇔g（x）=f（x）+4x单调递减或h（x）=f（x）-4x单调递增

点评：以上练习题中，运用法一分离变量转化为函数单调性问题求解，希望本文中解决双变量问题三个方法能给读者带来启发。