水工压力隧洞衬砌配筋的计算

2018-08-10何敏，户莹，李宁，刘波

西北农林科技大学学报（自然科学版） 2018年9期

何敏，户莹，李宁，刘波

( 1 西安理工大学土木建筑工程学院，陕西西安 710048；2 西北勘测设计研究院，陕西西安 710065 )

在水电资源开发以及交通道路工程建设中，常需修建各种用途的隧洞，其中后期过水的水工隧洞作为地下工程，其沿线地质条件复杂，不可预见因素较多，而不同的衬砌形式及配钢筋量决定了隧洞工程的投资与工期，直接影响着电站的经济效益与运行安全[1-2]，因此深入研究科学合理的水工压力隧洞配筋方法是十分必要的。

目前，内水压力作用下衬砌配筋计算主要采用边值法、公式法和一般有限元法[3-10]。其中边值法依据弹性力学厚壁圆筒理论，用解析法计算厚壁圆筒和围岩的位移、轴力、弯矩等；公式法假定混凝土衬砌已开裂，不再承担拉力，据此推导隧洞衬砌钢筋的应力应变以及钢筋面积公式等;而一般有限元法考虑到围岩作用的影响，通常使用梁单元或实体单元来模拟衬砌结构，然后根据求解得到的衬砌轴力和弯矩进行配筋计算。在有压隧洞结构设计中，对同一个设计项目用“公式法”进行计算可能只需要按构造配筋，而按边值法和常规有限元法计算则需要配置很多钢筋，差异巨大，以致于设计人员无所适从，最终大多还是凭经验进行结构设计[11-18]。

另外，边值法假设衬砌在承受内水压力过程中不会出现裂缝，但在实践中水工隧洞的衬砌往往会出现裂缝[17-19]，该假设与实际情况不符，这也是导致其计算配筋量较多的原因之一[20]。一般有限元法，特别是三维有限元模型能够更好地模拟地应力和地质因素的影响[21-23]，但对裂缝的模拟存在一定的局限性，仅能通过在衬砌块体之间设置间距来模拟裂缝[24]，并不能真实有效地模拟裂缝对配筋计算的影响。关培文[3]认为，虽然公式法的基本假定与水工压力隧洞中钢筋混凝土衬砌的实际受力状态基本一致，但其未充分考虑围岩的实际位移情况，单一地用钢筋允许应力取代实际应力值计算所需钢筋的面积，所以有时会得到“负”值。一般情况下，钢筋实际应力达不到钢筋的允许应力，为此关培文[3]给出了压力隧洞配筋公式法的改进思路，即先按无钢筋计算出混凝土应变，然后根据混凝土变形与钢筋变形协调条件得出钢筋应力，再以此应力对衬砌进行配筋。

笔者认为,关培文改进的方法主要存在如下不足：钢筋应力是由混凝土与钢筋完全协调条件得到，钢筋应变在开裂与未开裂处均匀分布，这与衬砌开裂后裂缝处钢筋应变远大于未开裂处钢筋应变的实际情况不符，致使分析得到的钢筋应力偏低，据此配筋可能不够安全。此外，改进公式法还存在围岩按弹性计算、混凝土衬砌与围岩完全接触的不足。

为克服目前常用衬砌配筋计算方法的不足，获得符合压力隧洞实际工作性态的配筋计算结果，本研究提出通过katona裂缝单元模拟衬砌中的裂缝，用特殊的跨缝筋单元模拟跨缝处钢筋与混凝土的相互作用，推求较为真实的衬砌、钢筋应力及裂缝宽度，然后进行相关设计条件判断确定最终的配筋方案，建立更符合压力隧洞实际工作性态的配筋计算方法，为压力隧洞的实际配筋计算提供参考。

1 压力隧洞配筋计算的数值分析模型

压力隧洞衬砌结构配筋计算模型中包括围岩、衬砌混凝土、钢筋、裂缝、岩石-混凝土界面等单元，其中围岩和衬砌混凝土单元采用常规六结点三角形等参数实体单元模拟，模型中采用的几类特殊单元描述如下。

1.1 界面单元

用katona界面单元进行裂缝、岩石-混凝土的界面的模拟[4,25-26]，单元模型如下图1。

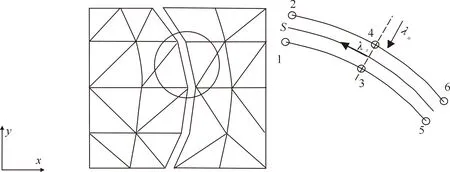
1～6.节点编号;λs、λn.分别为单元切向、水平向接触力1～6.Node numbers;λs,λn.Unit tangential and horizontal contact forces,respectively图1 裂缝、岩石-混凝土的界面单元模拟模型Fig.1 Interface model of cracks and rock-concrete

该单元满足以下附加约束方程：

(1)

式中：[C]*为坐标转换矩阵，[R]为接触状态矩阵，{u}、{λ}分别为待求解的节点位移和节点的接触力矢量，{f}*是已知节点相对位移或接触应力矢量。其中：

[C]*={-[T]*,[T]*}。

(2)

(3)

式中：[T]*为与节点状态有关的矩阵，{a}*为给定的结点相对位移。

当裂缝闭合，节点对之间无相对位移时，有：

(4)

式中：φ为裂缝面法向n与x轴间的夹角。

裂缝开裂时，节点对沿法向和切向的总接触应力均为0，则有：

(5)

式中：Ps为内水压力等效结点荷载。

将上面所述的微分方程进行联立求解，有：

(6)

式中：[K]为总体刚度矩阵，{F}为等效结点力。

为获得界面接触摩擦问题的正确解，需进行多次迭代求解。首先假定裂缝为接触状态，分别计算出相应接触刚度矩阵与等效荷载向量等，求解线性方程得到一组试验解，随后进行接触状态验证，判断假设状态是否正确。若不正确，假定新的状态，开始新一轮迭代，直到试验解与假定的状态匹配。

1.2 钢筋单元

考虑钢筋与混凝土界面作用的钢筋单元作用机理如图2所示。

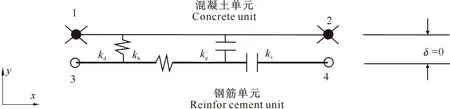
kb.钢筋轴向刚度;kd.“销栓”刚度；kg.钢筋长度方向上的剪切刚度；ks.钢筋横向剪切刚度；δ.单元厚度;1、2.单元实节点编号;3、4.单元虚节点编号kb.The axial stiffness of the steel bar;kd.The “pin bolt” stiffness;kg.The shear stiffness in the direction of the steel bar;ks.The transverse shear stiffness of the steel bar；δ.The thickness of the unit；1,2.The unit real node numbers;3,4.The unit virtual node numbers图2 考虑钢筋与混凝土界面作用的钢筋单元模型Fig.2 Reinforcement element considering the interaction between the rebar and concrete

对单元做以下假定：l)钢筋轴向变形呈线性分布，径向变形为常数；2)轴向力由钢筋传递，径向力忽略不计；3)在钢筋轴向上，钢筋和混凝土界面因位移不同而引起的剪应力由混凝土来承担；4)钢筋和混凝土界面间的横向刚度(“销栓”作用)用钢筋和混凝土之间添加的横向弹簧来模拟。则钢筋单元的刚度矩阵可表示为：

(7)

使用跨缝筋单元模拟裂缝处钢筋的作用机制，结果如图3所示。假定：1)跨缝钢筋的轴向力引起裂缝交界面上的摩擦作用；2)跨缝筋本身具有暗销作用。此外，裂缝处的滑移、开裂和闭合等对跨缝筋的受力状态也存在影响。

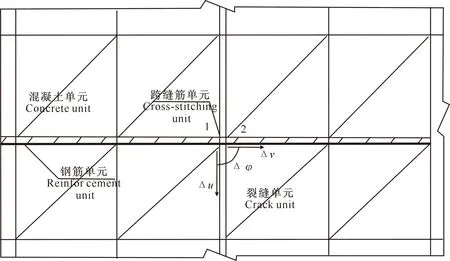
1、2.跨缝处节点编号1 and 2.The node numbers at the cross seam图3 裂缝处跨缝筋单元模拟Fig.3 Simulation of cross stitching unit at cracks

综合上述情况用有限元方程可导出：

(8)

式中：Kn为抗拉刚度；Kp为抗弯刚度，Ks为抗剪刚度，Δv为轴向位移增量；Δφ为偏转角度，Δu为侧向位移增量，Fn、Fm、Fs分别为轴向、弯曲及切向对应的结点荷载。其中：

(9)

(10)

(11)

(12)

式中：E为单元弹性模量;A为单元面积;l为跨缝筋单元的长度,l=0为裂缝未张开时跨缝筋单元结点对完全耦合在一起的情况;I为单元截面惯性矩;G为剪切模量。钢筋的侧向刚度折减系数随裂缝宽度的发展不断变化，其关系如图4所示。

v1～v3.分别取1.0，0.6，0.1；d1～d3.分别取0.1，0.5和2 mmv1～v3.Adopted as 1.0,0.6,0.1;d1～d3.Adopted as 0.1,0.5 and 2 mm图4 钢筋侧向刚度随裂缝宽度的演化曲线Fig.4 Evolution of lateral stiffness of reinforcing bar with crack width

2 压力隧洞衬砌配筋计算假定及思路

2.1 计算假定

(1)假定混凝土衬砌均匀裂成若干块；围岩和衬砌均按弹塑性材料考虑，钢筋按弹性材料考虑。

(2)衬砌未开裂处，混凝土与钢筋共同承担外荷载；衬砌开裂处，荷载全部由钢筋承担。

2.2 计算思路

首先假定衬砌裂缝条数n及配筋量ρ(可按公式法初步计算)，利用建议的数值模型进行计算分析，得到未开裂处混凝土衬砌中的应力σt、钢筋应力σs及裂缝宽度w，再进行如下判断及调整。

(1)进行混凝土应力验算，如果混凝土衬砌中的应力大于混凝土抗拉强度ft，表明衬砌中将有新的裂缝产生，需在模型中增加裂缝条数；反之，如果混凝土衬砌中的应力远小于混凝土设计抗拉强度，则应减少模型中裂缝条数，如此反复计算直至衬砌的应力接近混凝土的设计抗拉强度。

(2)进行裂缝宽度及钢筋应力验算，如果裂缝宽度或钢筋应力大于允许值，则通过增加配筋量来使两者均小于并接近其允许值；如果裂缝宽度及钢筋应力均远小于其允许值，则可通过减小配筋面积来使裂缝宽度和钢筋应力两者中一个接近允许值，此时的配筋量为设计所需的最小配筋量。

2.3 关键问题

裂缝宽度与钢筋应力的准确性是本研究与公式法(改进公式法)的根本区别，也是本研究配筋方法是否合理的关键。为此，应通过可靠方法验证分析得到的裂缝宽度与钢筋应力是否合理。

最大裂缝宽度可依据下式[27]估算：

Wmax=4εste,

(13)

(14)

其中：Wmax为最大裂缝宽度，εs为钢筋应变，te为与r和d有关的函数，d为混凝土保护层厚度，r为钢筋间距，A=drmm2。

在钢筋屈服前，εs=σs/Es,其中σs为钢筋应力，MPa；Es为钢筋弹模，取20×104MPa。将te和εs代入式(13)，可得：

(15)

公式(15)是美国钢筋混凝土建筑规范中推荐使用的裂缝宽度估算公式。这个公式考虑了钢筋应力、钢筋间距和混凝土保护层等因素对裂缝宽度的影响。本研究采用此公式对分析得出的裂缝宽度与钢筋应力关系进行验证。

3 工程实例分析

3.1 工程概况

表1 鲁地拉水电站引水隧洞围岩的物理力学参数Table 1 Physical mechanical parameters of surrounding rock of diversion tunnel of Ludila hydropower station

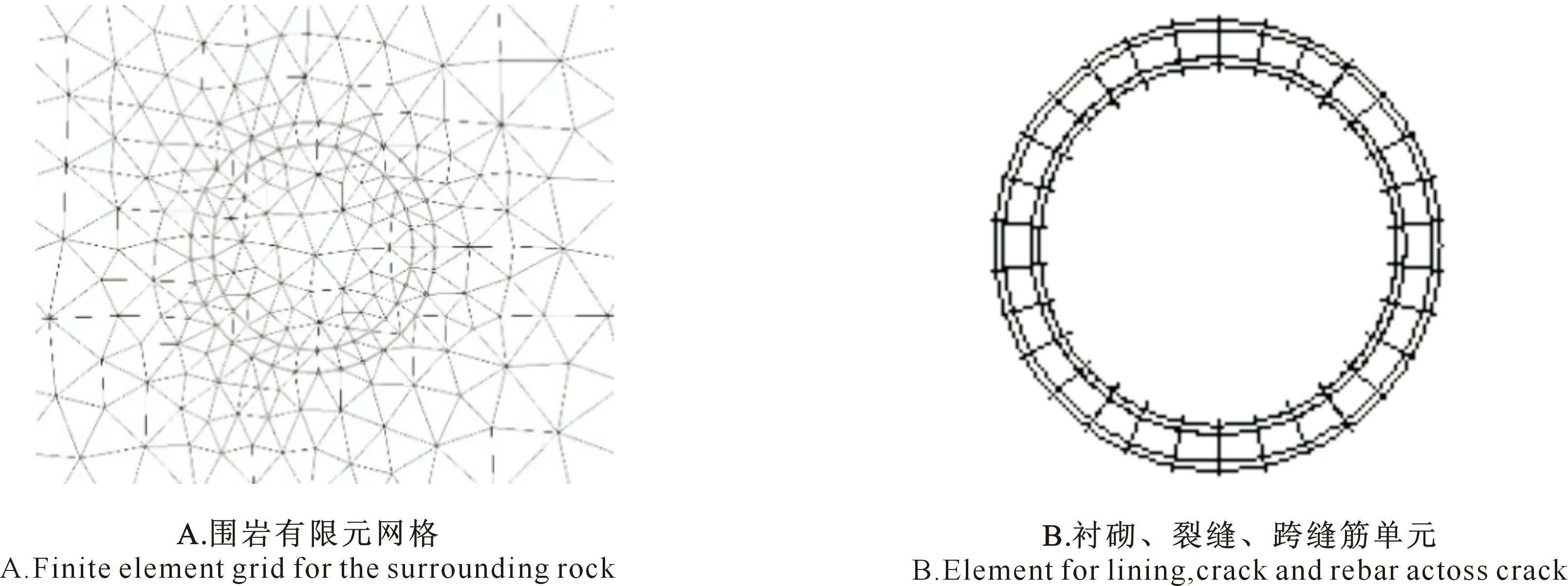
图5 鲁地拉水电站引水隧洞围岩及衬砌、裂缝、跨缝筋单元有限元网格Fig.5 Finite elements mesh of the surrounding rock,lining,crack and cross-seaming bars of the water diversion tunnel of Ludila hydropower station

计算条件：内水压力水头为1.3 MPa(130 m)，围岩为Ⅳ类，钢筋保护层厚度为25 mm，衬砌混凝土设计强度为1.3 MPa，钢筋设计强度为300 MPa。

3.2 配筋设计

按照本研究建议的数值分析模型计算分析，表2为不同裂缝条数时配筋和裂缝宽度对比结果。从表2可以看出，本研究方法计算得到的钢筋应力与裂缝宽度之间的关系与式(15)较吻合，表明分析得到的成果是可靠的。分析表明，随着裂缝条数增加，衬砌刚度降低，衬砌分担的应力减小，衬砌开裂处钢筋应力也随之减小。当裂缝条数为32条时，即衬砌中裂缝间距为0.53 m时，衬砌中的应力接近衬砌混凝土的设计强度，裂缝宽度在允许值(0.2 mm)以内，钢筋应力也在设计强度范围内。据此可确定当内水压力水头为1.3 MPa(130 m)，围岩为Ⅳ类时，衬砌所需最小配筋为5Φ25(4 900 mm2)。

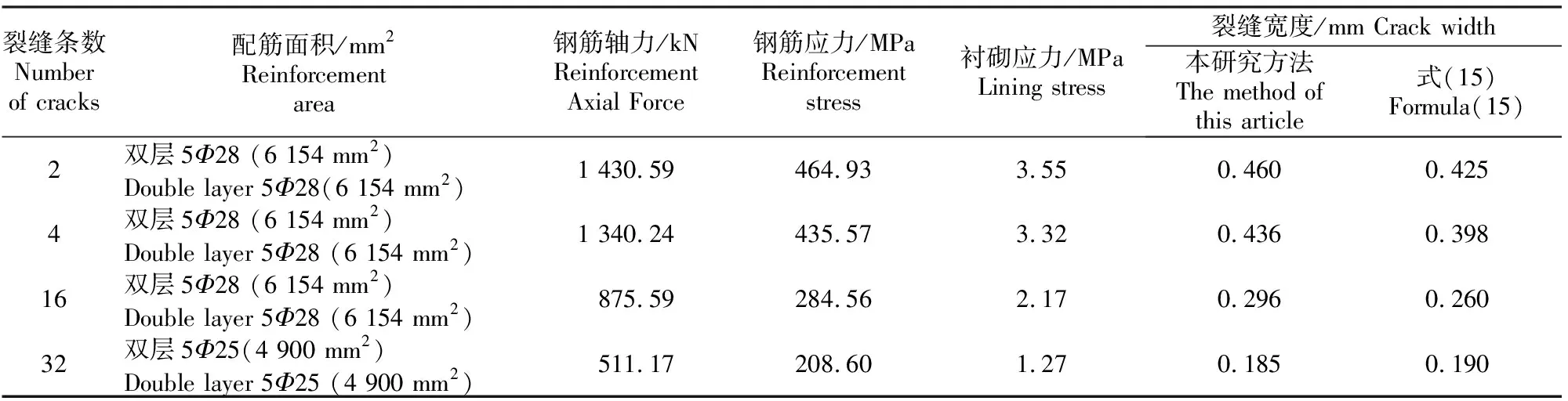
表2 不同裂缝条数时配筋和裂缝宽度对比Table 2 Comparison of reinforcements and crack widths with different numbers of cracks

表3给出了鲁地拉水电站引水隧洞衬砌按不同方法求解得到的配筋结果。由表3可以看出，用边值法计算出的结果特别大，主要是边值法假定未考虑衬砌开裂；公式法虽然假定衬砌开裂运行，但未考虑裂缝与钢筋的相互作用，即无法反映出裂缝界面上应力分布不均匀的特性，其计算出的钢筋应力比实际值小。本研究所建立的方法得出的配筋结果介于前两者之间，弥补了两种方法的不足，更为合理。

表3 不同计算方法所得配筋结果对比Table 3 Comparison of reinforcement results of different methods

3.3 结果验证

按照建议的方法完成了鲁地拉水电站引水洞的配筋设计，图6给出了水电站运行后引水洞下平段仪器R03-YSD5(1#引水隧洞，5-5断面，高程为1 120 m)测定的混凝土衬砌钢筋应力计实测值。

图6 鲁地拉水电站引水隧洞混凝土衬砌钢筋应力实测曲线Fig.6 Stress measurement of concrete lining of diversion tunnel at Ludila hydropower station

从图6可以看出，实测钢筋最大应力为134.77 MPa，与计算值208.6 MPa相比略低，这是因为计算分析中采用的内水压力1.3 MPa包括了甩负荷工况产生的水击压力，而图6给出的是正常运行工况混凝土衬砌钢筋计实测应力值，对应内水压力为1.01 MPa；按照实测结果推测，甩负荷工况(内水压力1.3 MPa)衬砌钢筋计对应的最大应力为175.21 MPa，接近于理论计算值，可见本研究方法的计算结果与实际较为吻合。