流冰对引水隧洞撞击破坏力学特性数值分析与验证

贡 力，李雅娴，靳春玲



流冰对引水隧洞撞击破坏力学特性数值分析与验证

贡 力，李雅娴，靳春玲

（兰州交通大学土木工程学院，兰州 730070）

寒旱地区冬季寒冷，昼夜温差大，长距离输水工程在解冻期易形成流冰，不同尺寸的流冰对隧洞形成不同的挤压力或撞击力，甚至导致衬砌破损，工程失效。该文通过深入研究流冰与引水隧洞碰撞时的相互作用问题，并利用有限元接触-碰撞算法的对称罚函数算法，进行了流冰撞击引水隧洞衬砌的接触-碰撞算法的理论分析。应用ANSYS/LS-DYNA软件，建立隧洞模型和流冰模型，选用LS-DYNA SOLVER求解器进行求解，分析流冰对隧洞的破坏程度；并通过物理模型试验采用几何比尺为C为28进行验证，揭示流冰对引水隧洞的撞击破坏机理。结果表明：流冰在不同流速、不同平面尺寸、不同厚度等工况下，流冰与隧洞衬砌碰撞时，隧洞衬砌表面会产生不同程度的变形和破坏；随着流速增大，撞击应力值也相应增大，两者呈线性关系；当流冰平面尺寸变化时，其撞击应力随着流冰平面尺寸的增大而增大，两者呈非线性关系；当流冰厚度增加时，流冰厚度小于0.5 m时，撞击力随着流冰厚度的增大而增大；其厚度超过0.5 m时，撞击应力值变化不大，其流冰平面尺寸和最大应力呈现近似线性关系。同时，通过软件模拟和试验观测得出的计算结果基本一致，流冰与隧洞衬砌碰撞时，隧洞衬砌表面会产生不同程度变形，变形对隧洞稳定性影响不大。但是，流冰冲刷会导致隧洞衬砌表面破碎，长期会影响结构的强度与稳定性。其结果可为寒旱地区冬季输水工程安全提供理论支撑和技术保障。

力学特性；数值模拟；模型；冰工程；引水隧洞；撞击力

0 引 言

中国西北地区位于高寒、干寒地带，冬季气温低，冰期长，为了缓解西部地区严重缺水的现状，中国先后在西部地区投资建设了引大入秦工程、引洮工程等大批引调水工程，用于农田灌溉、人畜饮水，目前筹建的南水北调西线项目更是投资空前[1]。然而如此规模庞大的投资建设，建成的项目却因遭受寒旱气候的影响，产生了诸如引水隧洞冻融破坏、引水隧洞地质缺陷渗漏等一系列问题，对结构安全性与供水效率产生严重影响。尤其是高寒地区冬季寒冷，昼夜温差大，在气温降低到0 ℃以下后，水流内首先会出现水内冰，水内冰经过发展逐渐形成冰花，继而堆积形成冰盖，至第二年解冻期，由于高寒地区温差大，冰盖融化过程中，易形成武开河或半文半武开河，产生的流冰，对引水隧洞造成不同的挤压力或撞击力，导致衬砌破损，直至工程失效，达不到规划建设的预期目标，进而造成受水区的供水分配压力，影响春季引水灌溉和春耕生产。因此，流冰对引水隧洞的破坏机理研究迫在眉睫。

国内外学者对冰期的冰情演变进行了研究，国内1921年在黄河下游对冰凌进行了首次科学观测[2]；Gilberto等[3]进行了弯道冰塞堆积的水槽试验，对冰塞堆积现象的一些特性开展了研究；茅泽育等[4-6]建立了基于河流动力学和热力学原理的冰水力学数学模型的基本流动路线图和相应程序；肖建民等[7]开展了冰盖的形成与消融原理方面的研究；王军等[8]通过冰塞堆积试验，使得冰塞的形成机理和规律方面的研究向前推进了一步；徐国宾等[9]在天津大学低温冰工程实验室进行了冰力学模型试验，探索了冰的膨胀力、冰盖稳定性和流冰对桥墩等水工建筑物的撞击力等冰力学问题；贡力等[10]对西部地区引水工程病害特点进行了研究和分析。综上所述，国内外的研究者对河流冰情演变规律研究较多，经历了从早期的原型观测、试验研究到现在广泛应用的数值模拟几个阶段，但国内外专门针对流冰对寒旱地区长距离输水工程中引水隧洞的影响研究较少。

为了研究寒旱地区长距离输水工程中解冻期流冰对引水隧洞的影响，本文采用理论分析、数值模拟和试验研究的方法，开展流冰对引水隧洞的衬砌撞击影响力的研究。运用ANSYS LS-DYNA建立流冰与引水隧洞之间发生碰撞的有限元模型，搭建流冰撞击引水隧洞试验单边坡试验装置，模拟隧洞中流冰与引水隧洞碰撞的全演变过程，发现流冰在不同工况下对引水隧洞的撞击力影响规律，为寒旱地区冬季输水工程安全提供理论支撑和技术保障。

1 流冰对引水隧洞撞击的数值模拟理论基础

一般描述各种非线性物质运动和变形以及碰撞等问题的控制方程有Lagrange法、Euler法两类。本文研究的接触-碰撞问题一般釆用Lagrange描述法。Lagrange法质点随着物体运动的过程中，其质量保持不变。流冰撞击隧洞边壁的过程中，质点在整个运动系统中必须保持能量守恒方程、质量守恒方程、动量守恒方程[11-14]。

1.1 质量守恒方程

式中0(, 0)为模型=0时刻的初始模型中的介质密度（kg/m3）；(,)为模型在时刻的构形介质密度（kg/m3）；(,)为模型的Jacobin行列式。

式中e为排列张量，X为物质坐标，x为空间坐标。

1.2 动量守恒方程

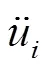
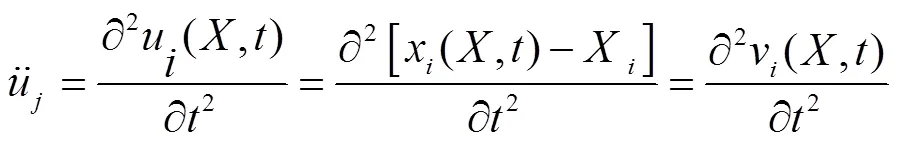
式中v(,)为质点在时刻坐标为的瞬时速度（m/s）。

1.3 能量守恒方程

式中v为质点在方向的瞬时速度，m/s；v为质点在方向的瞬时速度，m/s。

1.4 边界条件

隧洞模型现时构型的面力边界条件为：=n，其中为面元上的应力矢量，为现时构型有向面元，为现时构型的现时构型的应力张量。计算要求流冰与隧洞之间的整个运动过程当中，在求解范围内全部满足动量守恒方程式，但在实际工程问题中几乎不可能直接求解出结果。而数值计算方法可以从微分方程的弱形式角度考虑，只需在内积条件下得到基本动量方程，进而对模型的虚功率方程式进行推导，再经过有限元离散化后，得到模型的节点位移方程。通过加权余量法，选取虚速度作为加权系数，则动量方程的弱形式见式（7）。

式中v()为虚速度，其值根据下式（8）进行求解。

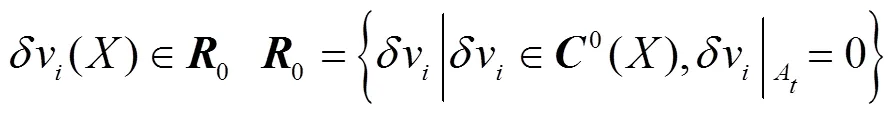
式中0，0分别为0时刻的向量和阻尼矩阵，A为模型的边界面，运用分部积分原理，接触面力的平衡式如式（9）所示。

那么，模型中任意质点的速度、加速度、虚速度及变形率可以写成方程组

把方程组（10）中的各方程写成矩阵形式，然后代入虚功率公式（9）中。整理后可得

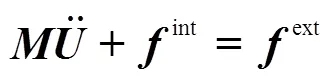
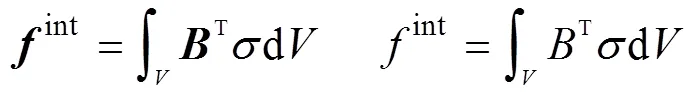
求解式（14），便可得出当下时刻的质点位移，进一步解得该时刻的结构应变与应力。

2 流冰对隧洞撞击模型的建立

2.1 工程实例

盘道岭3号隧洞全长15.723 km，纵坡1/1 000，设计流量为29 m3/s，最大流量为34 m3/s。该隧道为无压引水隧洞，洞身为混合式衬砌型式，一次衬砌为锚杆、喷射混凝土、钢筋网片和钢拱架，二次衬砌为现浇混凝土和钢筋混凝土，圆拱直墙、底板为反拱的断面，净宽4.2 m，净高4.4 m，顶为半圆，半径为2.1 m，反拱底板半径9.75 m，侧墙与反拱交接处加设贴角，贴角高0.404 m，水平宽0.337 m。隧洞前期支护隧洞断面图及模型图如图1所示。

注：C20为抗冻强度，F150为抗渗强度。

2.2 模型建立

ANSYS LS-DYNA具有ALE和Euler算法、热分析和流体-固体耦合分析功能、静力分析功能和隐式分析功能等，可以快速地求解平面或空间内高速碰撞、爆炸等动态非线性问题。采用ANSYS/LS-DYNA模拟流冰对隧洞的撞击。因此，流冰位于水面之上，所以在ANSYS/LS-DYNA软件模拟模型的荷载时，应忽略竖向荷载，如重力、浮力等，只考虑风、水流拖曳力等水平方向的荷载[15-16]。水平荷载主要通过流冰的初速度表达，体积不等、厚度不一的流冰分别以不同的速度作用于隧洞内壁时，各种不同工况下的撞击力也是不同的，通过建模来模拟计算流冰对隧洞的撞击力。

本文选取单面自动接触（automatic single surface contact, ASSC）接触类型。假设初速度，定义接触、边界条件后进行输出控制，利用动力学分析命令流文件（ANSYS软件中称为K文件）进行输入计算。在计算中，流冰和隧洞模型采用3D Solid164实体单元模拟；流冰和隧洞材料为线弹性材料；单元划分采用映射网格划分。隧洞衬砌面为主体，流冰接触面为从界面。参数见表1，其中冰的参数根据于天来等[17-18]对冰的弹性模量与冰的关系确定。

表1 隧洞和流冰物理性能参数

3 流冰对隧洞撞击模型的应用

由于流冰与隧洞在碰撞过程中，牵扯诸如动态、流固耦合等不稳定因素较多，是一个很复杂的冰结构之间相互碰撞的问题，影响因素主要有特征冰体的速度、平面尺寸、厚度、几何形状、抗拉强度、抗压强度、弹性模量、结构的柔性、摩擦力、碰撞角度等[19-21]。本文主要研究流冰在不同流速、不同流冰平面尺寸、不同流冰厚度等工况下流冰对引水隧洞边壁的撞击力。方便计算，计算中碰撞角度采用正碰，几何形状采用长方形，不考虑二次碰撞等问题，其隧洞流冰组合模型网格划分如图2所示。

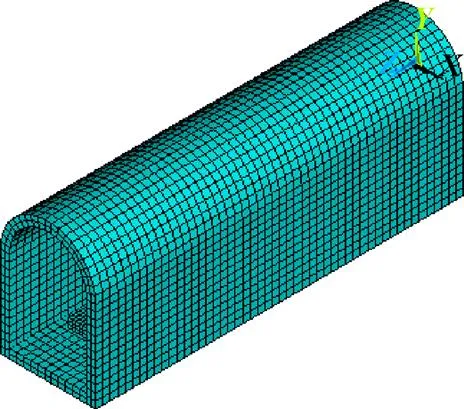
图2 隧洞流冰组合模型网格划分图

3.1 流速对撞击力的影响

数值模拟中选取水深为2 m，实际碰撞过程中流冰的尺寸不规则，参照徐国宾等[9]的试验，模拟流冰尺寸设置为2 m×0.5 m×2 m，根据引大入秦工程运营实际水流的控制流速，流速分别取0.5、0.8、1.0、1.3、1.5、1.8、2.0、2.3、2.5、2.8、3.0、3.5 m/s。在流冰允许破坏范围内，流冰在=0.5 m/s时撞击力最大应力云图如图3所示。

注：时间t=0.004 984 8 s，接触面取1.0 m2。v为流速，下同。

图3为流冰对隧洞的撞击力最大应力云图，由于撞击过程中撞击力为动态变化，当=0.004 984 8 s时，可以得到撞击力瞬间最大值为0.53×103kN。同理，可以得到不同流速相应的撞击力最大应力云图。通过云图可知，最大撞击力分别0.94、1.18、1.47、1.77、2.12、2.36、2.71、2.93、3.27、3.42、4.09×103kN。可以得到最大碰撞力随着流冰流速的变化关系曲线，如图4所示。

图4 最大撞击力-流速关系图

由图4可以看出，在其他工况不变的情况下，只改变流冰速度，流速对撞击应力极值有明显的影响，其撞击力随着流冰流速的增大而增大，其变化关系呈现出近似线性的关系。由于该模拟过程中接触面积为1.0 m2，可以发现，流冰流速与最大撞击力的关系近似如公式（12）所示。

=1.2（0.5m/s≤≤3.5 m/s） （12）

式中为流冰的流速，m/s；为流冰与隧洞边壁碰撞时所产生的最大撞击力值，kN。

由动能定理和动量定理可知，当同一质量物体的速度越大，它所具有的动能就越大，产生的撞击力就越大。但是，冰与普通物体（钢、铁、石头等）不同，冰在一定条件下由于其韧、脆转变典型特性的存在，超过一定大小的撞击力作用下，冰会发生破碎等现象，当冰破碎后，流冰尺寸变小，但仍然形成二次碰撞，由于涉及因素复杂，且影响小，本文不作计算。

3.2 流冰平面尺寸对撞击力的影响

为了研究流冰体积对隧洞衬砌作用力的影响，在不改变接触面的前提下，仅改变流冰平面尺寸。水深选取2 m，流冰流速选取=5 m/s，冰厚选取0.5 m，在其他参数固定不变的条件下，只改变流冰平面尺寸，分别取0.5 m×0.5 m×2 m、1.0 m×0.5 m×2 m、1.5 m×0.5 m× 2 m、2.0 m×0.5 m×2 m、2.5 m×0.5 m×2 m。平面尺寸分别为0.5 m×0.5 m的1、2、3、4、5倍。其实质是碰撞接触面积不发生变化，为1.0 m2，而流冰的体积和质量发生变化。在流冰允许破坏范围内，图5为流冰尺寸为1.0 m×0.5 m×2 m对隧洞的撞击力最大应力云图。

Note: t= 0.002 466 2 s, v=5 m×s-1

从图5可以看出，由于撞击过程中撞击力为动态变化，当=0.002 466 2 s时，可以得到撞击力瞬间最大值为4.34×103kN。同样的方法得到0.5 m×0.5 m×2 m、1.5 m×0.5 m×2 m、2.0 m×0.5 m×2 m、2.5 m×0.5 m×2 m的撞击力最大应力云图。对应的撞击力分别1.10×103、4.99×103、5.69×103、6.23×103kN。由接触面为1.0 m2，可以得到不同流速下的最大撞击应力分别为1.10、4.99、5.69、6.23 MPa。即可以得到在不同面积尺寸下，最大撞击力与流冰平面尺寸如图6所示。

由图6可以看出，在不改变流冰其他参数的情况下，只改变流冰平面尺寸时，撞击应力极值的变化明显，说明质量和体积的变化对撞击力有较大影响。由于在不同工况下接触面积均取1.0 m2，所以撞击应力关系曲线与撞击力关系曲线一致。当流冰平面尺寸较小时，其撞击应力随着流冰平面尺寸的增大而增大较为明显，但是当质量增大到一定值时，撞击力增加缓慢，其变化关系呈非线性的关系（流冰在发生韧、脆转变前）。

3.3 流冰厚度对撞击力的影响

为了研究流冰厚度对隧洞衬砌作用力的影响，水深选取2 m，选取引大入秦工程运营中的较大流速，取流冰流速=3 m/s，流冰平面尺寸选取2.0 m×2.0 m，在不改变其他参数的情况下，只改变流冰厚度，厚度分别取0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.1、1.2、1.3、1.5 m共12种工况。在流冰允许的破坏范围内，得到流冰厚度为0.3 m对隧洞的撞击力最大应力云图，如图7所示。

Note: t=0.007 451 s. v=3 m×s-1

由图7可以看出，由于撞击过程中撞击力是动态变化的，当=0.007 45 s时，可以得到撞击力瞬间最大值为1.58×103kN。同理，可以得到厚度为0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.1、1.2、1.3、1.5m的撞击力最大应力云图和局部应力云图。通过云图可知，撞击力分别1.58、2.26、3.42、4.02、5.10、5.49、6.34、7.08、7.37、8.40、9.15、10.47×103kN。当接触面取0.6、0.8、1.0、1.2、1.4、1.6、1.8、2.0、2.2、2.4、2.6、3.0 m2时，得到不同流速下的最大撞击应力分别为2.63、2.82、3.42、3.35、3.64、3.43、3.52、3.54、3.35、3.50、3.52、3.49 MPa。随之得到在不同厚度下，最大应力值与流冰厚度的关系、最大撞击力与流冰厚度关系如图8所示。

图8 流冰厚度与最大应力及最大撞击力关系图

由图8可知，当流冰厚度小于0.5 m时，撞击应力随着流冰厚度的增大而增大；其厚度超过0.5 m时，撞击应力值变化不大，最大应力呈现线性关系。撞击力与流冰厚度之间，当流冰厚度较小时，其撞击力随着冰厚度的增大而增大，其变化关系呈现出线性的关系。

综上结果看出：在不同流冰流速、不同流冰平面尺寸、不同流冰厚度等工况下，流冰与隧洞衬砌碰撞时，隧洞衬砌表面会产生不同程度的变形。这种变形对隧洞稳定性影响不大，但是，隧洞衬砌会产生表面破碎，经过长时间水流的冲刷，将会造成隧洞衬砌表面脱落等现象，破坏结构的强度和稳定性。

4 流冰对隧洞撞击的物理模型试验

4.1 试验设计

本文利用室内模型试验研究解冻期流冰对引水隧洞的碰撞作用。对不同流冰平面尺寸、不同流冰厚度、流冰速度等工况下流冰对引水隧洞的撞击力展开系统的室内模型试验[22-26]。本文中试验装置与原型的几何比尺C取为28，试验中液体采用普通水, 材料密度比尺取为1.0，在常重力场条件下进行试验, 加速度比尺C取为1.0[27-30]。模型试验装置图如图9所示，其中a，b，c，d，e点为应变片一侧的位置，另一侧对称布置，应变片位置高度为17 cm。

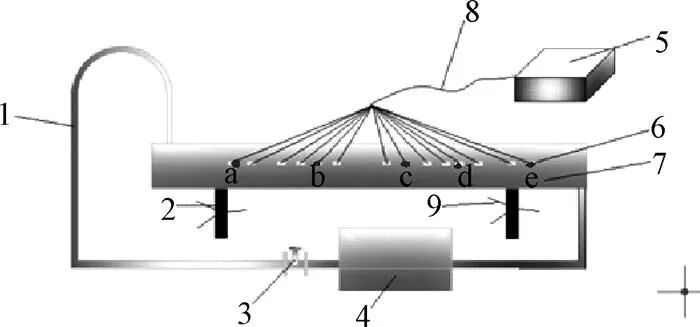
1.循环水管 2.固定支柱 3.水泵 4.水箱 5.测试仪器 6.应变片（a, b, c, d, e） 7.水槽 8.测试线 9.旋转螺旋

4.2 试验内容

根据试验设计，其具体试验步骤如下：

1）研究流速对撞击力的影响试验。在水箱中充满水；打开总电源，利用泵使得水箱中的水冲入水槽；将准备好的若干规格为7 cm×3.5 cm×7 cm冰块放入水槽中；利用旋转螺旋来调节流速；用流速计测得流速为0.5 m/s；利用水位探针确定水深，根据几何比尺，水深为17.2 cm；在隧洞模型两边边壁水面线位置分别贴10个有机玻璃应变片；使瞬态应变测试仪处于关闭状态；利用测试线将应变片与瞬态应变测试仪链接，每个应变片与瞬态应变测试仪上面的接头对应相连；打开瞬态应变测试仪，调成手动装置；随着冰块碰撞隧洞边壁，依次在瞬态应变测试仪上度数，读出应变值；记录数据，处理数据；接着改变流速大小使得流速分别为0.5、0.8、1.0、1.2、1.5、1.8、2.0、2.3、2.5、2.8、3.0、3.5 m/s，重复上述步骤，观察流速对撞击应力的影响。

2）流冰平面尺寸大小对撞击力的影响试验。改变工况，水深为17.2 cm；流速为3.0 m/s，改变冰块尺寸分别取1.8 cm×1.8 cm×7 cm、3.5 cm×1.8 cm×7 cm、5.5 cm× 1.8 cm×7 cm、7.0 cm×1.8 cm×7 cm、9.0 cm×1.8 cm×7 cm；重复上述步骤，测试流冰平面尺寸对撞击应力的影响。

3）流冰厚度对撞击力的影响试验。流速和冰块厚度一定，冰块平面尺寸为变量进行试验，具体为：选定水深为17.2 cm，流速为3.0 m/s，流速和平面尺寸一定，改变冰块尺寸分别取1.1、1.4、1.8、2.14、2.5、2.9、3.2、3.6、3.9、4.3、4.6、5.4 cm；重复上述步骤，测试流冰平面尺寸对撞击应力的影响。

4.3 流速对撞击力的影响

按照试验步骤1）开展试验，得到不同流速下，隧洞边壁所受的撞击力及应力值，将上述试验数据处理后，按照模型相似比进行计算，其软件模拟计算结果、试验观测计算结果对比图如图10 a所示。可以发现，在流速不同的条件下，数值模拟值与试验值有大致相同的趋势，吻合性较好，总体来说，随着流速的增大，流冰对隧洞的撞击力力增大，且基本程线性分布关系。模拟值与试验值的最大误差为1.83%，最小误差为0.04%，平均相对误差为0.94%，在允许范围内[28]。由此可知，本文采用的计算模型准确可靠，模拟结果可信。分析可知，误差主要是试验值波动导致，可能与试验中流冰的二次碰撞有关。

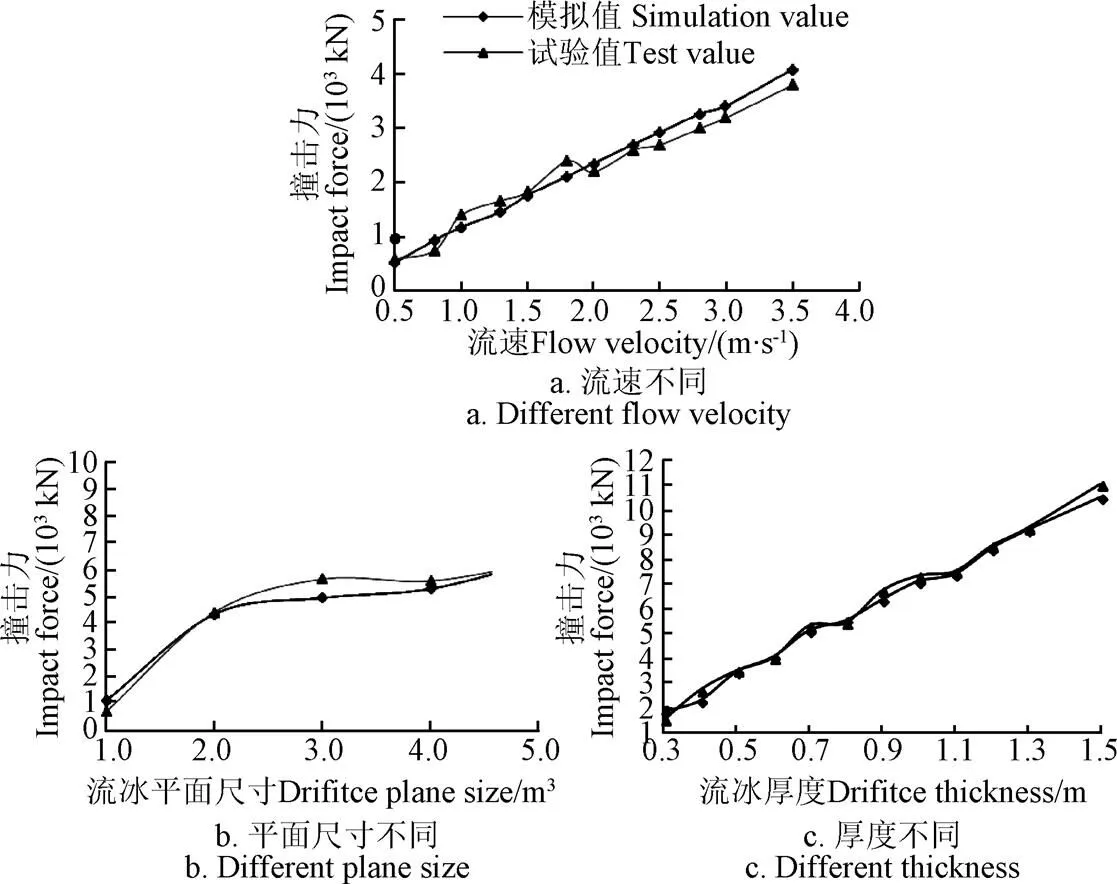
图10 试验结果与模型计算结果对比图

4.4 流冰平面尺寸大小对撞击力的影响

按照试验步骤2）开展试验，得到不同平面尺寸下，隧洞边壁所受的撞击力及应力值，将上述试验数据处理后，按照模型相似比进行计算，可以得到试验结果与模型计算结果对比图10b，观察图可以发现，当流冰平面尺寸较小时，其撞击应力随着流冰平面尺寸的增大而明显增大。但是当平面尺寸大于1.2 m2以后，撞击力的增量趋缓，说明当面积增大时，冰水粘滞力和拖曳力增加，使得撞击力变缓。通过计算可知，试验值与模型值最大误差为2.24%，最小误差为0.05%，平均相对误差为1.15%，在允许范围内[29]，吻合性较好。

4.5 流冰厚度对撞击力的影响

按照试验步骤3）开展试验，根据试验的测算，流冰的厚度不同，隧洞边壁所受的撞击力及应力值也不同，将上述试验数据处理后，按照模型相似比进行计算，可以得到试验结果与模型计算结果对比图10c，观察图可以发现，在流冰厚度不同的条件下，模拟值与试验值有大致相同的趋势，吻合性较好，总体来说，随着流冰厚度的增大，流冰对隧洞的撞击力增大，且基本程线性分布关系。模拟值和试验值结果吻合性较好，最大误差为1.98%，最小误差为0.06%，平均相对误差为1.02%，在允许范围内[30]。由此可知，本文采用的计算模型准确可靠，模拟结果可信。

5 结 论

本研究应用有限元接触-碰撞算法建立流冰撞击引水隧洞衬砌作用时的数值计算仿真模型，并相应地开展室内模型试验，数值模拟结果和试验结果良好吻合，并根据流冰的流速、平面尺寸、厚度等参数变化对引水隧洞破坏力学特性得到以下结论：

1）随着流冰流速的增大，流冰对隧洞衬砌的碰撞力增大，且流冰流速对隧洞最大撞击力之间存在线性关系（=1.2），试验值与计算误差在5%以内。因此，在满足供水要求的情况下，解冻期运营要控制流速，减小流冰对隧洞衬砌的撞击力。

2）流冰在平面尺寸增大时，其实质是体积和质量增大，当流冰平面尺寸小于1.0 m2时，其撞击应力随着流冰平面尺寸的增大而明显增大，但是当流冰平面尺寸超过1.0 m2时，撞击力增加缓慢，二者之间呈非线性的关系。说明流冰质量增加后，水流的挟冰能力下降，撞击力变缓。

3）流冰厚度小于0.5 m时，撞击力随着流冰厚度的增大而增大；其厚度超过0.5m时，撞击应力值变化不大，说明冰水粘滞力和拖曳力增加，使得撞击力变缓。

实际工程中冰水两相之间的运动是非常复杂的，其间存在着粘滞力、拖曳力等多因素耦合影响的问题；流冰与隧洞衬砌之间的碰撞是不规则的，在模拟流冰与隧洞的碰撞时，碰撞角度选取的形式等问题，需要做进一步的研究。

[1] 杨开林. 长距离输水水力控制的研究进展与前沿科学问题[J]. 水利学报，2016，47(3)：424－435.

Yang Kailin. Review and frontier scientific issues of hydraulic control for long distance water diversion[J]. Journal of Hydraulic Engineering, 2016, 47(3): 424－435. (in Chinese with English abstract)

[2] 张成，王开. 冰期输水研究进展[J]. 南水北调与水利科技，2006，4(6)：59－63.

Zhang Cheng, Wang Kai. The relational research and experience of water transfer during freezing period[J]. South-to-North Water Transfers and Water Science& Technology, 2006, 4(6): 59－63. (in Chinese with English abstract)

[3] Gilberto E U, Robert E. Bend ice jams: Laboratory observations[J]. Canadian Journal of Civil Engineering, 1992, 19: 855－864.

[4] 茅泽育，吴剑疆，张磊，等. 天然河道冰塞演变发展的数值模拟[J]. 水科学进展，2003，14(6)：700－705.

Mao Zeyu, Wu Jianjiang, Zhang Lei, et al. Numerical simulation of river ice jam[J]. 水科学进展, 2003, 14(6): 700－705. (in Chinese with English abstract)

[5] 茅泽育，赵升伟，相鹏，等. 冰盖下水流流动的掺混特性[J]. 水利学报，2005，36(3)：291－297.

Mao Zeyu, Zhao Shengwei, Xiang Peng, et al. Turbulentmixing characteristics of ice-covered river flow[J]. Journal of Hydraulic Engineering, 2005, 36(3): 291－297. (in Chinese with English abstract)

[6] 茅泽育，许昕，王爱民，等. 基于适体坐标变换的二维河冰模型[J]. 水科学进展，2008，19(2)：214－223.

Mao Zeyu, Xu Xin, Wang Aimin, et al. 2D numerical model for river-ice processes based upon body-fitted coordinate[J]. Advances in Water Science, 2008, 19(2): 214－223. (in Chinese with English abstract)

[7] 肖建民，金龙海，谢永刚，等. 寒区水库冰盖形成与消融机理分析[J]. 水利学报，2004，35(6)：80－85.

Xiao Jianmin, Jin Longhai, Xie Yonggang, et al. Study on mechanism of formation and melting of reservoir ice cover in cold area[J]. Journal of Hydraulic Engineering, 2004, 35(6): 80－85. (in Chinese with English abstract)

[8] 王军，陈胖胖，江涛，等. 冰盖下冰塞堆积的数值模拟[J]. 水利学报，2009，40(3)：348－354+363.

Wang Jun, Chen Pangpang, Jang Tao, et al. Parameter model of water-conducting device specification for indirect subsurface drip irrigation[J]. Journal of Hydraulic Engineering, 2009, 40(3): 348－354+363. (in Chinese with English abstract)

[9] 徐国宾，李大冉，黄焱，等. 南水北调中线输水工程若干冰力学问题试验研究[J]. 水科学进展，2010，21(6)：808－815.

Xu Guobin, Li Daran, Huang Yan, et al. Laboratory study of problems in ice mechanics encountered in the Middle Route of South-to-North Water Transfer Project[J]. Advances in Water Science, 2010, 21(6): 808－815. (in Chinese with English abstract)

[10] 贡力，靳春玲. 西部干寒地区引水明渠病害特点及治理措施[J]. 建设监理，2014(12)：66－68, 73.

Gong Li, Jin Chunling. The characteristics and treatment measures of open diversion canal diseases in dry and cold regions of western China [J]. Journal of Construction Supervision, 2014(12): 66－68, 73. (in Chinese with English abstract)

[11] 李钊. 石头河水库灌区东干渠水流数值模拟研究[D]. 西安：西安理工大学，2009.

Li Zhao. Research on the Stream Numerical Simulation of Shitou River Reservoir Irrigation District East Main Channel[D]. Xi’an: Xi’an University of Technology, 2009. (in Chinese with English abstract)

[12] Zufelt J E, Ettema R. Fully coupled model of ice-jamdynamics[J]. Journal of Cold Regions Engineering, 2000, 14(1): 24－41.

[13] Shen Hungtao, Sun Junshan, Liu Lianwu. SPH simulation of river ice dynamics[J]. Journal of Computational Physics, 2000, 165(2): 752－770.

[14] 陈明千. 西藏高寒地区引水渠道冰花生消规律研究[D]. 成都：四川大学，2006.

Chen Mingqian. Study on the Process of Ice Formation and Melting in Diversion Channel of Tibet[D]. Chengdu: Sichuan University, 2006. (in Chinese with English abstract)

[15] 吴素杰，宗全利，郑铁刚，等. 高寒区多口融冰井引水渠道水温变化三维模拟及井群优化布置[J]. 农业工程学报，2017，33(14)：130－137.

Wu Sujie, Zong Quanli, Zheng Tiegang, et al. 3D simulation on water temperature change of diversion channel and optimal arrangement of multi-wells at high altitude and cold regions[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(14): 130－137. (in Chinese with English abstract)

[16] Betchelor G K. Mass transfer from small particles suspended in turbulent fluid[J]. Journal of Fluid Mechanics, 1980, 98(3): 609－623.

[17] 于天来，袁正国，黄美兰. 河冰力学性能试验研究[J]. 辽宁工程技术大学学报：自然科学版，2009，28(6)：937－940.

Yu Tianlai, Yuan Zhengguo, Huang Meilan. Experimental study on mechanical behavior of river ice[J]. Journal of Liaoning Technical University: Natural Science, 2009, 28(6): 937－940. (in Chinese with English abstract)

[18] 张凤德，李广一. 基于LS-DYNA的流冰撞击坝体仿真计算[J]. 水利建设与管理，2013，33(2)：19－21.

Zhang Fengde, Li Guangyi. Simulation of flow ice impact on dam body based on LS-DYNA[J]. Water Conservancy Construction and Management, 2013, 33(2): 19－21. (in Chinese with English abstract)

[19] 李抗彬，沈冰，李智录，等. 基于非恒定水流模拟的灌区明渠水力响应特征分析[J]. 农业工程学报，2015，31(10)：107－114.

Li Kangbin, Shen Bing, Li Zhilu, et al. Open channel hydraulic response characteristics in irrigation area based on unsteady flow simulation analysis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(10): 107－114. (in Chinese with English abstract)

[20] 王亚玲，刘应中，缪国平. 圆柱绕流的三维数值模拟[J]. 上海交通大学学报，2001，35(10)：1464－1469.

Wang Yaling, Liu Yingzhong, Miao Guoping. Three-dimensional numerical simulation of viscous flow around circular cylinder[J]. Journal of Shanghai Jiaotong University, 2001, 35(10): 1464－1469. (in Chinese with English abstract)

[21] 张宽地，吕宏兴，陈俊英. 马蹄形过水断面临界水深的直接计算法[J]. 农业工程学报，2009，25(4)：15－18.

Zhang Kuandi, Lü Hongxing, Chen Junying. Direct calculation of critical depth of horseshoe section tunnel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(4): 15－18. (in Chinese with English abstract)

[22] 李炜. 水力计算手册[M]. 北京：中国水利水电出版社，2006.

[23] 张成. 南水北调中线工程非恒定输水响应及运行控制研究[D]. 北京：清华大学，2008.

Zhang Cheng. Research on Response of Unsteady Water Transport and Operation Control in the Middle Route of the South-to-North Water Diversion Project[D]. Beijing: Tsinghua University, 2008. (in Chinese with English abstract)

[24] 韩延成，高学平. 长距离自流型渠道输水控制的二步法研究[J]. 水科学进展，2006，17(3)：414－418.

Han Yancheng, Gao Xueping. Two-step optimal operation and control method for long distance gravity-flow delivery in canals[J]. Advance in Water Science, 2006, 17(3): 414－418. (in Chinese with English abstract)

[25] 高霈生，靳国厚，吕斌秀. 南水北调中线工程输水冰情的初步分析[J]. 水利学报，2003，34(11)：96－102.

Gao Peisheng, Jin Guohou, Lü Binxiu. Preliminary study on ice regime in the middle route of south to north water transfer project[J]. Journal of Hydraulic Engineering, 2003, 34(11): 96－102. (in Chinese with English abstract)

[26] 李家春. 现代流体力学发展的回顾与展望[J]. 力学进展,1995，25(4)：442－450.

Li Jiachun. Retrospects and prospects of fluid mechanics[J]. Advances in Mechanic, 1995, 25(4): 442－450. (in Chinese with English abstract)

[27] 刘孟凯，王长德，冯晓波. 长距离控制渠系结冰期的水力响应分析[J]. 农业工程学报，2011，27(2)：20－27.

Liu Mengkai, Wang Changde, Feng Xiaobo. Analysis on the hydraulic response of long distance canal control system during ice period[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(2): 20－27. (in Chinese with English abstract)

[28] 王晓玲，周正印，蒋志勇，等. 考虑气温变化影响的引水渠道水内冰演变数值模拟[J]. 天津大学学报：自然科学与工程技术版，2010，43(6)：515－522.

Wang Xiaoling, Zhou Zhengyin, Jiang Zhiyong, et al. Numerical simulation of frazil ice evolution in diversion channel considering effect of temperature variation[J]. Journal of Tianjin University, 2010, 43(6): 515－522. (in Chinese with English abstract)

[29] 成都科学技术大学水力学教研室. 水力学（下册）[M]. 北京：人民教育出版社，1979.

[30] 王晓玲，张自强，李涛，等. 引水流量对引水渠道中水内冰演变影响的数值模拟[J]. 水利学报，2009，40(11)：1307－1312.

Wang Xiaoling, Zhang Ziqiang, Li Tao, et al. Numerical simulation of diversion water flux effect on frazil ice evolution in diversion channel[J]. Journal of Hydraulic Engineering, 2009, 40(11): 1307－1312. (in Chinese with English abstract)

Numerical simulation and verification on impact damage mechanical property of drift ice on diversion tunnel

Gong Li, Li Yaxian, Jin Chunling

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

In high latitude region of western China, the environment is in harsh condition that it is cold and dry in winter and has long ice period, which causes many water resource problems. In order to relieve the serious water shortage condition in cold and dry region, a large number of long distance water diversion projects were established to improve the water resource condition, such as increasing farm irrigation, human and animal drinking. While the ice damage occurs frequently under severe ice conditions in cold and dry region, especially in ice period in winter and thawing period in spring, it is easy to form drift ice with different velocities, different plan sizes and different thicknesses, which produces different extrusion forces or impact forces to damage tunnel lining, causing project failure. The failure project could not realize the original planning and construction goal, giving rise to the water allocation pressure. The water allocation would cause water shortage which influences diversion irrigation and farming production in spring. Based on the intense researches on the collision simulation problem of the interaction between drift ice and diversion tunnel, this paper used the symmetric penalty function in the finite element contact-impact algorithm to conduct the theoretical study on collision simulation problem between drift ice and water diversion tunnel. ANSYS/LS-DYNA was adopted as the platform to establish tunnel model and drift ice model. LS-DYNA SOLVER was used as the solver to solve and analyze the damage degrees of drift ice on tunnel. The physical model tests were conducted to verify and reveal the impact damage mechanism of drift ice on diversion tunnel. The physical model was constructed by the geometric scale of 28, which is the ratio of the experiment facility to the prototype in the test. The results show that tunnel lining surface will form varying degrees of deformation and failure when the tunnel lining is impacted by the drift ice with different velocities, different plane sizes and different thicknesses. It is also discovered that the impact stress increases with the flow velocity and their relationship presents linear variation. The impact stress also increases with the drift ice’s plane size and their relationship presents nonlinear variation. The impact stress increases with the drift ice thickness when the drift ice thickness is less than 0.5 m. While the drift ice thickness is greater than 0.5 m, the maximum stress value shows little change. The relationship between drift ice’s plane size and maximum stress shows approximately linear variation. Meanwhile, the software simulation and test observation results are almost the same. The impact of drift ice on the tunnel lining would cause the deformation of lining, but the deformation has little influence on the tunnel stability. The drift ice’s long time erosion would cause the tunnel lining surface to fall off, and further break the strength and stability of the tunnel structures. The study supplies theoretical support and technical guarantee for water diversion project security in cold and dry region of western China.

mechanical performance; numerical simulation; models; ice engineering; diversion tunnel; impact force

贡 力，李雅娴，靳春玲. 流冰对引水隧洞撞击破坏力学特性数值分析与验证[J]. 农业工程学报，2018，34(13)：144－151. doi：10.11975/j.issn.1002-6819.2018.13.017 http://www.tcsae.org

Gong Li, Li Yaxian, Jin Chunling. Numerical simulation and verification on impact damage mechanical property of drift ice on diversion tunnel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(13): 144－151. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.13.017 http://www.tcsae.org

2018-03-12

2018-06-01

国家自然科学基金项目（51669010，51541902）；甘肃省自然基金（17JR5RA105，17JR5RA101）

贡力，教授，博士，主要从事输水工程安全的研究。Email：gongli@mail.lzjtu.cn

10.11975/j.issn.1002-6819.2018.13.017

TV672

A

1002-6819(2018)-13-0144-08