基于负载和互感参数摄动的电动汽车无线充电控制

王立业, 岳 圆， 王丽芳, 廖承林, 张玉旺

(1.中国科学院电力电子与电气驱动重点实验室(中国科学院电工研究所), 北京市 100190; 2. 北京电动车辆协同创新中心,北京市 100081; 3. 天津大学电气自动化与信息工程学院， 天津市 300072)

0 引言

随着环境污染问题日益严重,能源危机日益迫切,在这种大背景下,大力发展以电动汽车为代表的新能源汽车是中国汽车工业应对能源与环境挑战,实现可持续发展的必然选择[1]。电动汽车的发展和推广应用受充电设施的建设、充电的安全与方便性等影响较大,目前电动汽车的充电方式主要包括接触式(插电式)和非接触式(无线)充电。目前电动汽车无线充电起步较晚,尚处于研发和示范运行阶段[2]。然而,电动汽车无线充电相比有线充电有着环境适应性好、便捷性高、与电网的互动能力更强等诸多优势[3],因此它有着更巨大的应用前景。电动汽车无线充电系统要求输出功率在较宽范围内可调,输出电压、电流稳定,而无线电能传输系统的传输功率和效率对谐振线圈和负载的参数极其敏感,负载参数的变化、线圈横向、纵向距离的轻微改变等轻微摄动都会导致系统输出功率发生明显变化[4]。由于无线充电系统的输出特性复杂,其自身参数的时变性和不确定性,以及外界的扰动等都会导致输出特性发生显著变化[5],参数变化对于无线电能传输的输出控制也是一大问题,目前的研究中主要有如下三种解决方法。

1)补偿参数结构优化设计与动态调谐,通过选取特定的阻抗匹配串并结构,利用非线性规划等算法优化补偿电路的参数,使得当负载参数变化时,系统的输出电压、频率等参数基本不变[6],或者在谐振补偿网络中加入可调电感、可调电容,结合一定的控制算法,通过调节可控电感、电容使负载变化时线圈的谐振频率保持不变[7]。但是这种方式通常只适用于负载参数变化,互感参数的变化无法应对。

2)基于参数辨识的控制,利用实时测取的电压电流信息,对负载参数、互感进行实时检测估计,将得到的估计结果再给到控制系统中,调节控制参数[8-9]。参数在线辨识对检测信号的即时性要求较高,由于原副边通信速率问题,一般在线参数辨识使用的是原边电压电流信息,对于耦合复杂的电路拓扑参数辨识难度较大。同时,该方法对电路参数测量也有较高的要求。

3)利用鲁棒性较高的智能控制算法,例如模糊控制算法、鲁棒控制算法输出反馈对系统进行闭环控制。由于控制算法本身具备一定的鲁棒性,当参数摄动时,可以在无需辨识的情况下保证输出的稳定性[10]。

由于系统模型较为复杂,因此智能控制算法的设计具有一定的难度和复杂性。另外,由于磁耦合无线电能传输(WPT)系统传输特性对参数变化敏感,智能控制算法的动态特性相对较差。针对以上方法的问题本文对基于不确定参数的无线充电控制进行了研究,目的是使在无线系统参数扰动时系统能够稳定输出。首先,针对参数的时变和不确定性,建立了系统的不确定性状态空间模型并设计了鲁棒性强的鲁棒H∞控制器,将其简化得到了更利于实际应用的鲁棒比例—积分—微分(PID)控制器。然后,针对实际充电应用中的需求,应用移相和调频相结合的逆变器控制方式对PID控制器进行了试验验证。

1 闭环控制方案

对于LCCL匹配拓扑结构下的无线充电系统,由于电感电容元件较多,导致系统的阶数很高。同时电路中逆变器和整流桥的存在,使得系统具有非线性特性。通过分析负载阻值、互感值、频率等参数对系统传输特性的影响,可以看出系统特性对参数的变化较为敏感。因此需要将系统进行线性化建模,同时设计一个鲁棒性较强的控制器,使控制系统对参数变化不那么敏感,参数摄动时仍能保证系统稳定、快速响应。

因此本文采用原边单边控制的结构,在原边进行电压电流检测并进行其负载电流估算,取代传统的副边输出电流检测再通信回原边的方式,利用估计得到的负载电流进行闭环反馈控制。

2 负载电流估算

系统的不确定量或者说可变参数主要包括负载等效电阻和线圈互感两个参数,等效负载值和互感值对系统的输出电流都有影响。而在电流Ip和功率Pp通过测量已知的时候,由有功功率守恒可知,只需要负载参数的值就可计算得到负载电流的值,因此首先需要对负载参数进行辨识。

LCCL系统等效电路模型如图1所示。

图1 LCCL系统等效电路模型Fig.1 Equivalent circuit model of LCCL system

为了降低测量点电压,提高电压电流测量精度,选择电容C11的电压Up为电压测量点,原边线圈电流Ip为电流测量点,对电压电流进行测量可以得到电压电流有效值,以及此处的有功功率Pp、无功功率Qp等。通过计算可以获得以电容C11向后看的电路等效阻抗Z11。显然已知Cp,Lp和频率的情况下,可以得到负载折算到原边的阻抗Zsp为:

(1)

式中:Z11为电容C11向后看的电路等效阻抗;Lp为原边线圈电感;Cp为原边串联电容;ω为角频率。

利用阻抗分析法对Zs和Zsp进行研究,其中整流桥及后端负载用等效电阻Req替代,且Req=8RL/π2。可以得到如下关系式:

(2)

(3)

式中:Zs为副边等效阻抗;Xs为副边阻抗虚部;Rs为副边阻抗实部;ZLs为副边线圈电感阻抗;ZCs为副边串联电容阻抗;ZC21为副边并联电容阻抗;ZL21为副边串联电感阻抗;XLs为副边线圈电感阻抗虚部;XCs为副边串联电容阻抗虚部;XC21为副边并联电容阻抗虚部;XL21为副边串联电感阻抗虚部;Rls为副边线圈阻抗实部;Zsp为原边的阻抗;Xsp为原边的阻抗虚部;Rsp为原边的阻抗实部;M为互感。

通过上式,不难发现,Zsp中,负荷电阻RL和M是耦合在一起的,即无法通过Zsp的值直接辨识得到RL。为了完成两个参数的解耦,需要寻找单独变量作用的参数。通过观察可以发现,Zsp中互感M以乘积形式存在,Zsp的实部和虚部的比值可以将M消去,得到RL的函数式,从而可以完成对RL的求解。

令k=Xsp/Rsp,则

(4)

式中:Xc=1/(ωC21);C21为副边并联电容；A,B,C为常数,满足关系如附录A式(A1)所示。

(5)

将RL代入式(2)中,即可得到Rs的值。利用有功功率守恒,可得:

(6)

式中:Rp为原边电阻；Rlp为原边串联电阻;Is为副边电流;Po为副边功率;IRL为负载电流;Ptrans为线圈上传输的功率。

根据式(6)推导可得负载电流的表达式为:

(7)

3 无线充电系统状态空间建模

3.1 广义状态空间建模方法

无线充电系统中包含逆变器和整流桥等非线性器件,使得系统呈现非线性特性,而广义状态空间平均法建模(GSSA)可以将非线性系统近似线性化。广义状态空间平均法建模,其基本思想是将一个时域的周期信号进行傅里叶级数展开,然后用共轭的低阶谐波分量来近似原始信号,最后通过信号还原得到时域的原始信号包络和其近似解[11-13]。

时域连续周期信号x(t)在周期T内的傅里叶级数展开为:

(8)

式中:n为第n次谐波分量;〈x〉k(t)为x(t)的k阶傅里叶级数的系数,也即n次谐波分量的幅值;ω0=2π/T。

傅里叶级数具有多个运算特性,其中,式(9)表示微分特性,式(10)表示共轭对称性,分别可以表示为:

(9)

jIm(〈x〉k(t))

(10)

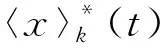
无线充电系统中,原边的高频逆变器和副边的整流桥都是开关非线性环节,为了描述系统的开关非线性特性,定义开关函数s(t),使其具有以下二值逻辑,即

(11)

式中:T为逆变器开关周期;θ为函数初相角;n为周期的整数倍;逆变环节中s(t)的逻辑值1和-1分别为电源向系统正向、反向注入能量;在整流环节中,s(t)的逻辑值1和-1分别为系统对负载正向、反向输出能量。

根据式(8),s(t)的傅里叶级数展开可表示为:

(12)

定义逆变环节的开关函数为sinv(t),整流环节开关函数为srec(t),sinv(t)初始相位可以设置为0,根据电路分析可知整流桥输入电压与逆变器输出相位差为90°,因此两个开关函数可以分别表示为:

(13)

(14)

根据以上分析,利用广义状态空间平均方法可以把无线充电系统的时域非线性微分模型转化为频域线性微分模型,从而建立状态空间模型。

3.2 无线充电全系统建模

无线充电系统电路模型如图2所示。

图2 LCCL-LCCL系统等效电路模型Fig.2 Equivalent circuit model of LCCL-LCCL system

由于系统中电感、电容等储能元件较多,并且将傅里叶系数实部和虚部分离的过程中使得状态变量数量翻倍,广义状态变量数量太多,显然不利于系统分析和控制器的设计。考虑到实际系统中可能变化的电路参数主要是互感和负载等效电阻,因此可以将其他电路元件当做常量处理,同时实际移相控制中,系统频率稳定不变,保留负载、互感等变量,而对阻抗匹配网络进行一定的电路简化,从而实现降阶的目的。系统简化电路模型见附录A图A1。

1)整流桥负载可以等效为一个电阻元件Req,其中Req=(8/π2)RL。

2)Req,L21,C21经过阻抗变化后为一个复数阻抗,取其实部为RL′,虚部为C21′,其中:

(15)

式中:C21为副边串联电容；L21为副边串联电感。

3)将串联的Lp,Cp以及Ls,Cs合并为Lp′和Ls′,即

(16)

式中:Ls为副边线圈电感;Cs为副边串联电容。

则系统的时域微分方程可以表示为:

(17)

式中:Vdc为直流输入电压;L11为原边串联电感;uc11为原边并联电容电压;C11为原边并联电容;iL11为原边并联电容电流;ip为原边电流;Rp为原边串联电阻;uc21为副边并联电容;is为副边电流。

傅里叶级数展开后的频域线性微分方程为:

(18)

将上述方程中各电路变量的傅里叶系数实部和虚部分离,依次定义为广义状态变量,即

x(t)=[Re〈iL11〉1Im〈iL11〉1Re〈uC11〉1Im〈uC11〉1Re〈ip〉1Im〈ip〉1Re〈is〉1Im〈is〉1Re〈uC21〉1Im〈uC21〉1]T

(19)

取逆变器的输入直流电压Vdc为系统的控制量u(t),则以上式作为状态变量的广义状态空间模型可以表示如式(20)所示，参数A1，B1,k的值见附录A式(A1)至式(A4)。

(20)

由于对电路进行了相应的简化,系统输出电流并没有作为状态量列入状态方程中,但是可以根据已有的状态量得到。由有功功率守恒,可以得到:

(21)

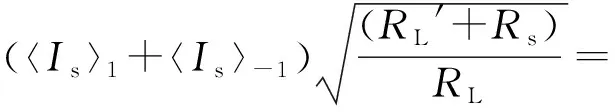
(22)

式中:IRL为负载电流。

则有输出矩阵C1,D1为:

(23)

4 鲁棒控制器设计

4.1 参数摄动下的不确定性模型

利用广义状态空间方法建立了系统的状态空间模型,然而系统的参数不确定性在模型中并不能体现,因此需要在以上模型的基础上再建立包含参数不确定性的系统不确定性模型。利用MATLAB的鲁棒控制工具箱提供的不确定性模型建模函数ureal,umat,uss等,直接建立实数参数、复数参数、矩阵等的不确定性模型。根据实际工况,可以确定负载等效电阻和线圈互感的取值区间。恒流充电过程中,负载RL在[35,50]Ω之间变化,而考虑恒压充电和启动的情况下,负载变化区间为[35,350]Ω。互感考虑线圈横向和纵向偏移,此处取20%的偏差范围。利用ureal函数对不确定参数进行建模有:RL=ureal(‘RL’,40,‘percent’,[-15,700]),M=ureal(‘M’,21.81e-6,‘percent’,[-20,20])。

将不确定参数带入状态空间模型中,可以得到状态空间的不确定性模型。利用usample指令可以使含有不确定参数的模型产生随机样本,从而观测不确定性模型在参数变化区间内的响应范围。不确定性模型的开环时域响应见附录A图A2。图中红线为负载RL=40 Ω、互感M=21.81 μH时的开环响应曲线,图中的上下边界分别为RL=35 Ω、互感M=26.17 μH和RL=350 Ω、互感M=17.48 μH。从图中可以看出,在参数变化的区间范围内,所有的开环响应最终都能够达到稳定状态。

4.2 鲁棒控制器求解

将H∞控制理论应用到实际系统的时候,最重要的是确定广义控制对象和加权函数,因为需要将要求的控制性能指标全部反映到广义控制对象和加权函数上。因为H∞控制的功用主要在于抗干扰控制以及对模型不确定度的鲁棒性,因此广义控制对象的选择上,首先需要找出实际中存在的干扰,并将它的输出响应作为评价输出的一部分,并且将它的频率特性的估值作为加权函数。系统的控制框图如附录A图A3所示,其中C是H∞控制器函数,P是无线充电系统传递函数,其输入为逆变器输出电压,输出为原边估计得到的电流值。d为输出扰动,代表测量扰动导致的输出电流扰动。加权函数Wd和Wu分别是描述干扰特性和参数不确定性的加权函数。根据干扰特性和不确定性特性,加权函数的取值可表示为:

(24)

式中:s为复数;e为系统输出。

干扰d到评价输出zd,zu的闭环传递函数为:

[zdzu]=[WdSWuT][d]

(25)

式中:S=1/(1+PC),T=C/(1+PC),S和T分别为灵敏度函数,P和C为附录A图A3的传递函数。

控制系统设计目标即是寻找一个稳定的控制器,使得闭环系统内部保证稳定的同时,干扰输入d到评价输出z的闭环增益范数小于1或指定性能参数γ,即:

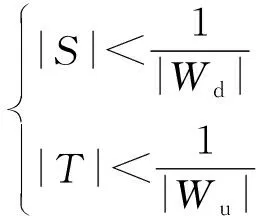
(26)

利用MATLAB求解鲁棒控制器是基于线性矩阵不等式的方法,因此需要基于MATLAB创建开环连接(附录A图A3中除去控制器模块的其他部分),将各个模块框连接起来并转化为矩阵形式。系统的开环结构框图如附录A图A4所示,其中G为开环广义控制对象,C为待求解的鲁棒控制器,D和u是开环系统G的输入,Zd,Zu,e是其输出。

在MATLAB中采用hinfsyn函数求解,求解得到的控制器C(s)是一个与给定线性非时变(LTI)系统阶数相同的传递函数/状态方程,其输入为输出反馈与参考值的误差,输出为控制量参数。本系统中,系统阶次为10阶,加权函数的阶次为1阶,综合出来的控制器为阶次为11的状态方程,其传递函数形式为:

(27)

式中:b1，b2,…,b12;a1，a2,…,a12为传递函数系数。

4.3 鲁棒PID控制器设计

由于求解得到的鲁棒H∞控制器阶数较高,模拟电路很难实现这样的高阶次控制器,若采用数字控制器,原则上能够实现该算法。但是,由于系统阶次较高,需要将控制器进行复杂的离散化处理,大大增加了设计复杂度和控制器的在线计算量,而且不利于在线调整参数。因此将前面得到的鲁棒H∞控制器进一步简化为具有鲁棒特性的PID控制器,以便于实际应用。

鲁棒H∞控制器的状态空间描述为:

(28)

式中:z为输出;u为反馈;e为参考值和反馈的加权值。

根据控制器的频域特性,可以用下述方法来近似获得高阶控制器的PID形式如下。

1)对E1进行相似变换,使得其为零的特征值和非零的特征值分开,即

(29)

式中:a为不含为零的特征值。

2)对F1和G1进行相应的变换为:

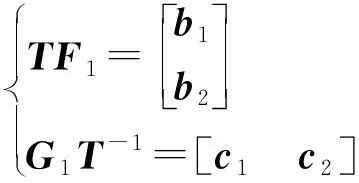
(30)

那么,高阶控制器的PID近似为Kp+Ki/s+Kds,其中,Kp=H1-c2a-1b2,Ki=c1b1,Kd=-c2a-2b2。

上述方法也即是根据频率变量s找到控制器的麦克劳林级数的对应项系数为:

G1(sI-E1)-1F1+H1=[c1c2]·

(31)

简化得到的PID控制器近似了高阶控制器的低频部分,忽略了其高频分量。为了验证鲁棒PID的近似效果,对两个控制器在不同负载和不同互感下的闭环响应进行了仿真,结果如图3和附录A图A5所示,Io/Iref表示输入电流与参考电流的比值。由图可以看出,鲁棒PID控制器对H∞控制器有较好的近似作用。负载电阻以及互感变化时,PID控制器响应更快,超调略大;但最终输出电流都能较快地稳定到参考值。鲁棒控制器对负载和互感参数的摄动有较强的鲁棒性,闭环系统的动态响应速度较快,稳态误差较小,控制精度较高。

图3 不同负载下鲁棒控制器和PID控制器闭环时域响应Fig.3 Closed loop time domain response of robust controllers and PID controllers under different loads

5 试验验证

5.1 系统硬件结构

为了验证设计的系统具有较好的鲁棒性,搭建无线充电系统硬件测试平台。平台由高频逆变器、发送/接收端线圈及其阻抗匹配电路、接收端整流电路、发送端电流电压传感器与检测电路、现场可编程门陈列(FPGA)控制与驱动电路、充电状态指示电路组成。系统的硬件实物图如附录B图B1所示。

5.2 系统控制框图

对于无线充电系统控制,频率调节比较敏感,且不是单调区间,移相调节范围比较窄,不能满足输出功率的需求,因此采用了移相加调频的控制方式。基于原边电流估算进行闭环控制,系统的整体控制框图如图4所示。

图4中包含了调频控制部分和移相控制部分。其中,虚线框中为无线电能传输系统(WPT),分为原边和副边两个部分。调频和移相控制分别构成闭环,调频控制中不断扫频,将负载电流与乘以裕度倍数的参考电流Iref作比较,两者相等时的频率确定为系统的工作频率f。移相控制中,负载电流与参考电流作差,经过鲁棒PID控制器得到逆变器输出电压Vi的值,通过f(u)函数模块将其转化为移相角α的形式,其中f(u)模块为对应的输出电压Vi和相角α的对应关系函数。调频和移相过程分开进行,FPGA控制器利用得到的控制量f,α生成对应的脉冲宽度调制(PWM)触发脉冲作用在驱动上,完成对逆变器的控制。

图4 无线充电系统控制框图Fig.4 Control chart of WPT

5.3 实验结果与分析

系统开始工作时,移相角置零,频率由低到高进行扫频,当输出电流达到参考电流的裕度倍数k时停止,即确定为系统工作频率。开始充电后,频率保持不变,采用移相控制方式,以实现输出功率的精细调节,适应负载和互感的扰动。

系统参数见附录B表B1,根据频率单调性和功率需求,调频范围选择为[4.5×104,5.3×104]Hz,移相角范围为0～90°,电流裕度倍数k=1.2。为了方便实验,将负载选择为电阻负载进行研究。

1)调频控制

线圈偏移d=10 cm,线圈之间互感M≈0.8M0;负载电阻RL=30 Ω,参考电流Iref=5 A,输入直流电压300 V。逆变器输出电流、输出电压、驱动,负载电流波形如附录B图B2所示,

线圈偏移d=0,线圈之间互感M=M0;负载电阻RL=30 Ω,参考电流Iref=5 A,输入直流电压300 V,系统电压电流波形如附录B图B3所示。

线圈偏移d=0,线圈之间互感M=M0;负载电阻RL=30 Ω,参考电流Iref=2 A,输入直流电压300 V,系统电压电流波形如附录B图B4所示。

上述三种情况分别对应:最大偏移,正常情况,小参考电流三种情况。从上面三个图可以看出,三种工况下,系统分别工作在52,50,46 kHz三个频率点下,移相角约为70°。系统稳态输出电流与参考电流误差值在0.1 A,控制误差在2%以内,逆变器输出电压、输出电流波形存在可容忍的小幅毛刺。

2)移相控制

系统频率确定后,系统开始移相控制,以对输出电流进行精细调节。在系统频率f=5×104Hz,参考输出电流Iref=5 A,线圈偏移d=0,输入直流电压300 V时的情况进行移相控制的实验研究。

负载扰动,闭环控制系统要求在负载以及互感存在扰动的时候,保证较高的控制精度和较快的动态响应。首先对负载的变化进行研究,不同的负载条件下,系统的稳态电压电流波形,以及负载跳变的动态过程波形,分别如附录B图B5至图B8所示。可以看出,当负载变化时,通过移相控制,能够有效地调节负载输出电流。电阻为30 Ω和80 Ω时,稳态下移相角分别约为70°和10°,系统的稳态电流误差均小于0.1 A,控制精度满足要求。负载分别由30～80 Ω和80～30 Ω跳变时,在移相控制的作用下,负载电流均在10 ms内达到重新恢复稳态,说明该鲁棒PID控制器具有较快的动态响应能力,针对负载参数扰动具有较高的鲁棒性能。

互感扰动,同样选取系统频率f=5×104Hz,参考电流Iref=5 A,线圈初始偏移d=0,输入直流电压300 V时的情况进行实验验证。主动对线圈施加横向偏移,使偏移距离为5 cm,系统稳态下的电压电流波形如附录B图B9所示。可以看出,当系统的互感参数扰动时,以偏移增大为例,互感减小,通过移相控制使移相角减小,输入功率增加,从而实现输出电流的调节。线圈的互感值与偏移成非线性变化,偏移越大,互感减小的比例越大,当d=5 cm时,M≈0.95M0;d=10 cm时,M≈0.8M0。图中可以看到,d=5 cm时,稳态时的输出电流实现恒流控制,电流误差约为0.05 A,控制误差约1%。

实验结果表明,控制系统对负载以及互感的扰动具有较好的鲁棒性,能够实现误差2%以内的控制精度,以及动态时间10 ms以内的快速响应。

6 结语

本文针对电动汽车无线充电系统参数的时变性和不确定性,建立了系统的不确定性状态空间模型,依据模型设计了鲁棒性强的鲁棒H∞控制器,并将其简化得到了更利于实际应用的鲁棒PID控制器。试验结果证明了该闭环控制系统具有较好的稳定性,并且能够容忍设计范围内的参数不确定性。本文设计的无线充电系统的控制策略,重点在控制方法和控制器的设计上,而并没有加入保护策略以及故障预警、处理环节。后续需要在这个方面加以完善,才能更好地投入实际使用。本文中的控制系统虽然是基于特定系统得出的,但它具有一定的通用性,对电动汽车无线充电系统的控制系统设计和优化有一定的参考价值。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。