接触网波速的仿真识别及试验验证

莫志刚，邹 栋，周 宁

(1.华中科技大学 土木工程与力学学院，湖北 武汉 430074；2.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

对于电气化高速列车，安装于列车顶部的受电弓在静态抬升力作用下升至架空接触网，实现滑动接触过程中的电能传输。而弓网系统取流质量的好坏，与其动力学性能直接相关[1]。就接触网而言，其动力学性能受接触网单跨内刚度分布和弹性振动(简称波动)传播的影响[2]。在高速运行条件下，波动传播成为影响弓网系统取流质量的主导因素。 同时，作为接触网弹性和惯性的综合度量因子，波动速度对接触网风振特性[3]和几何参数[4]同样存在显著影响。

就接触网波动现象而言，Dahlberg研究了欧拉梁上波动传播对梁变形的影响，开创了基于梁模型研究接触网波动现象之先河[5]；Aboshi等则研究了弓网接触压力受弹性波干扰时的变化规律[6]；Takamassa， Manabe等则依据行波动力学理论，主张在接触网或受电弓上安装阻尼器以抑制弹性波对弓网相互作用的影响， 从而提升弓网受流质量[7-8]；Zhou采用数值仿真技术，在研究接触网的波动传播特征参数的基础上，提出了改善接触网波速利用率的主要途径[9]。针对接触网波速识别，常丽将吊弦对接触线、承力索的作用简化为外加集中力和惯性力，采用欧拉梁模型等效接触线、承力索，基于模态叠加法推导了接触网的波速公式[10]；类似地，刘志刚将接触网等效为带张力的欧拉梁，研究接触网波速受气动阻尼影响的变动规律[11]； Sung基于小波变换分析方法，利用不同位置处接触网实测信号的小波脊线时间差，以及小波系数相关函数分析接触网的波动传播速度随振动频率变化规律[12]。 实际上，接触网属于低频、密频柔性结构，基于等效梁理论模型[10-11]的波速计算结果与接触网实际波速存在显著偏差。 此外，在利用小波识别接触网波速过程中[12]，小波的母函数类型及其参数的选择过于灵活， 难以给出稳定可靠的识别结果[13]，从而难以推广应用。

从工程设计角度来看，接触网波速是列车运行极限速度的限制速度之一[14]。 从而，波速大小的准确识别是接触网结构设计是否合理的必要条件。因此，本文采用有限元技术，仿真研究接触网在阶跃载荷作用下的波动传播规律，同时借助非接触式摄影测量设备，对实际接触网的振动特性展开试验研究。结合仿真研究和试验验证结果，提出一种利用仿真位移等值线图识别接触网波速的方法，以期为接触网设计参数的检验与验证提供简洁而可靠的解决方案。

1 弹性振动波速识别方法

对于由连续介质组成的弹性体，介质质点间存在着相互作用的弹性力。当外界激扰引起某质点偏离平衡位置而产生运动时，其周围质点在弹性力作用下发生牵连运动。这种由弹性力引起的连续介质起伏运动称为“弹性波”。考虑类似接触网线缆这种一维弹性体的弹性波传播，当不计结构阻尼的影响，且弹性力在介质中均匀分布时，一维弹性体上各质点振动响应时程曲线形状相似且幅值相同，但是不同位置处质点振动幅度抵达最大值的时刻不同。该时间差和对应质点的空间距离表征了弹性波的传播速度，可为基于振动响应等值线图识别弹性体波动传播速度提供理论依据。

双参数函数的等值线图由其参数空间上具有相等函数值的曲线组成，能够描述函数在参数空间上的分布和变化规律。令等值线函数取为一维弹性体质点振动响应(位移、速度或加速度)，且函数参数分别设置为质点空间位置和质点振动历经时间。那么，就相应于某一振动响应幅值的等值线而言，包含了不同空间位置处质点振动响应抵达该幅值的时间信息。从而该等值线的斜率，即空间位置对时间的比值，表示了该振动响应幅值遍历弹性体各质点的速度，即弹性波传播速度。因此，下文采用时空坐标下振动响应等值线图来识别弹性体的波动传播波速。

在将“时空坐标下振动响应等值线图识别弹性体波动传播速度方法”应用于实际接触网之前，先对该方法的可行性和准确性进行验证。考虑到欧拉梁和接触网同属连续介质弹性体，其弹性波形成机理相同。若时空坐标下欧拉梁的位移等值线图可以识别其弹性波的波速，那么时空坐标下接触网的位移等值线图理论上亦可识别其弹性波的波速。因此，利用欧拉梁弹性波传播速度的解析解对以上提出的方法进行验证。

1.1 欧拉梁波速的理论计算

张力作用下梁欧拉梁模型如图1所示。图中：E和I分别为欧拉梁的弹性模量和截面惯性矩；T为欧拉梁张力；A和ρ分别为欧拉梁的截面积和线密度。

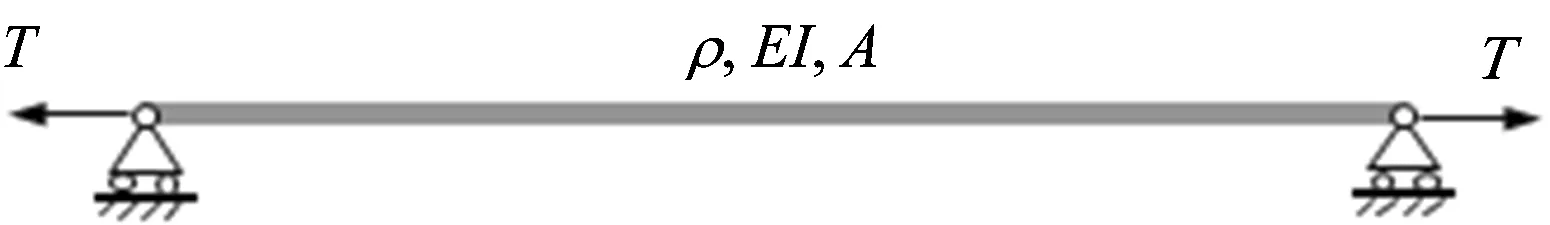
图1 欧拉梁模型

图1所示欧拉梁模型的运动方程为

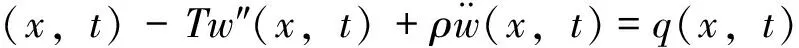
(1)

式中：w(x，t)为x处截面在t时刻的位移；q(x，t)为梁上x处截面在t时刻的均布载荷。

基于分离变量法，在模态空间Y(x)内将式(1)对应齐次方程的非零解展开为

w(x,t)=Y(x)eiωt

(2)

式中：ω为模态振动频率。

将式(2)其代入式(1)，经过推导[5]可得欧拉梁理论波速cbeam_theo为

(3)

1.2 欧拉梁波速的仿真识别

取400 m长欧拉梁模型，并将其线密度设为0.987 kg·m-1，截面抗弯刚度设定为130 N·m2，欧拉梁单元尺寸设为1 m，两端施加张力12 kN并配以简支位移约束。在距左侧梁端95 m处施加频率为2 Hz的简谐激励，以产生持续传播的弹性波。为提高仿真结果精度，仿真时间步长设为弹性波传播1个单元所需时间的1/10。

图2为欧拉梁跨中质点对应的位移响应时程曲线及其频谱分析结果。从图2 (a)中可以看出：该质点在0.8 s之前几乎不发生振动，位移幅值为0；0.8 s过后，跨中质点运动幅度增大，在2.5 s时幅度第2次增加。从图2 (b)中可看出：该质点振动响应主频与激励频率一致(为2 Hz)，从而说明前述仿真参数的设定，能成功模拟欧拉梁弹性波的传播特征。

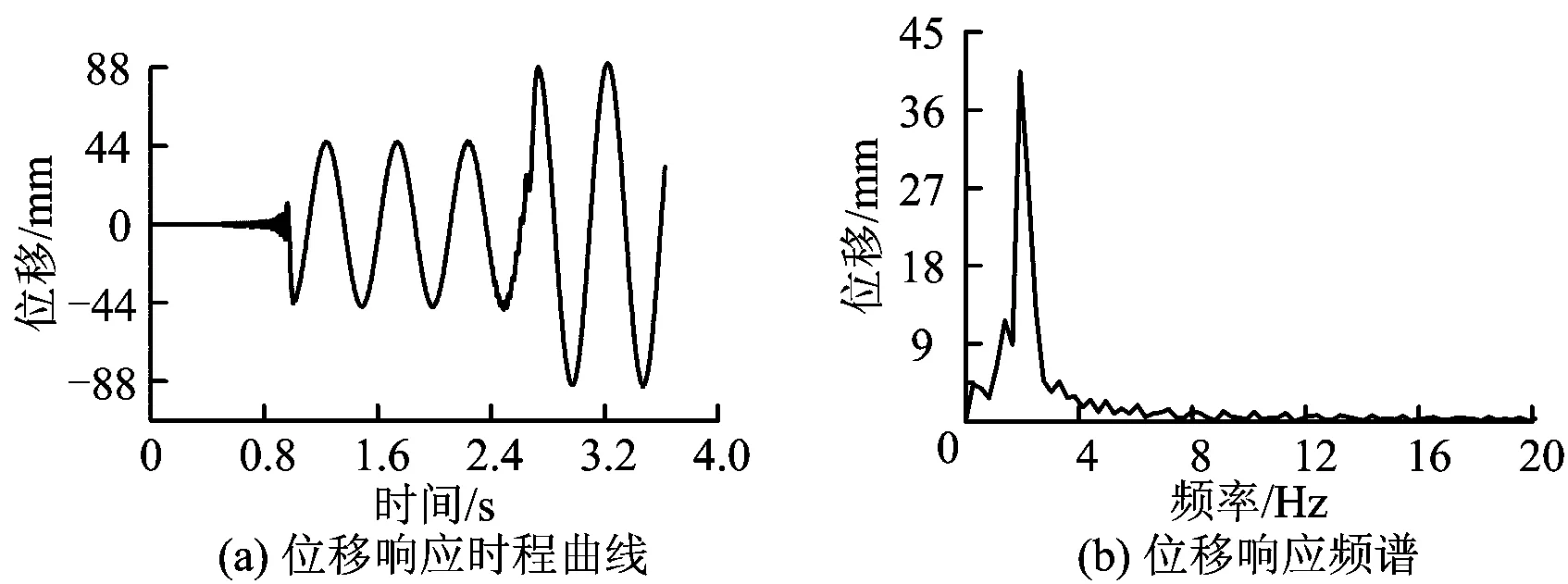
图2 欧拉梁跨中质点的位移响应

提取欧拉梁上各质点振动位移，在时空坐标下绘制位移等值线图，如图3所示，对前述欧拉梁的弹性波波速进行识别。从图3可以看出：95 m处简谐激励在梁上激起的2个行波分别往两侧传播，先后到达梁端点后发生反射并继续回传，如此往复而形成有规律的等值线图案。

通过提取图3中虚线所示左右行波对应的等值线，利用Matlab软件计算其斜率分别为109.67和110.80 m·s-1，取其平均值以估计简支欧拉梁的仿真波速cbeam_simu= 110.24 m·s-1。而当激励频率为2 Hz时， 由欧拉梁弹性波传播速度理论计算式(3)得到的理论波速cbeam_theo=108.84 m·s-1。从而，仿真识别与理论计算结果相对误差为1.28%。由此可知，利用位移等值线图能够准确预测欧拉梁中弹性波的波速。

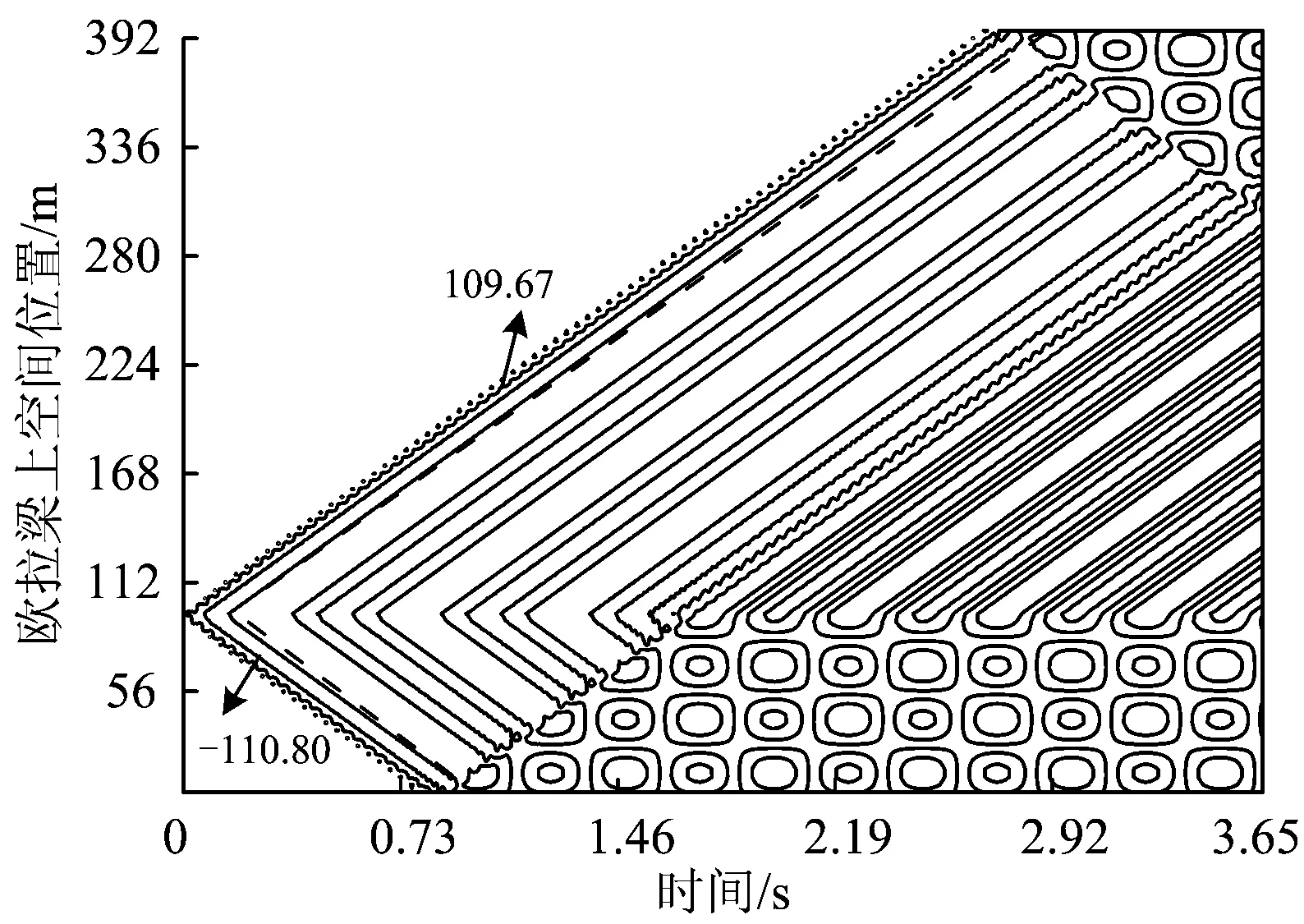
图3 欧拉梁位移响应等值线图(单位：m·s-1)

2 接触网波速仿真识别

2.1 接触网模型

为降低仿真分析时模型的误差，增加仿真和试验结果的可比性，以试验现场的3跨接触网为研究对象，基于有限元方法建立仿真模型。该接触网实验模型依据京津城际铁路接触网按1∶1比例设计，其工作高度为1.6 m，跨距长54 m，且每跨配置7根吊弦，如图4所示。该接触网实验模型的主要结构参数见表1。

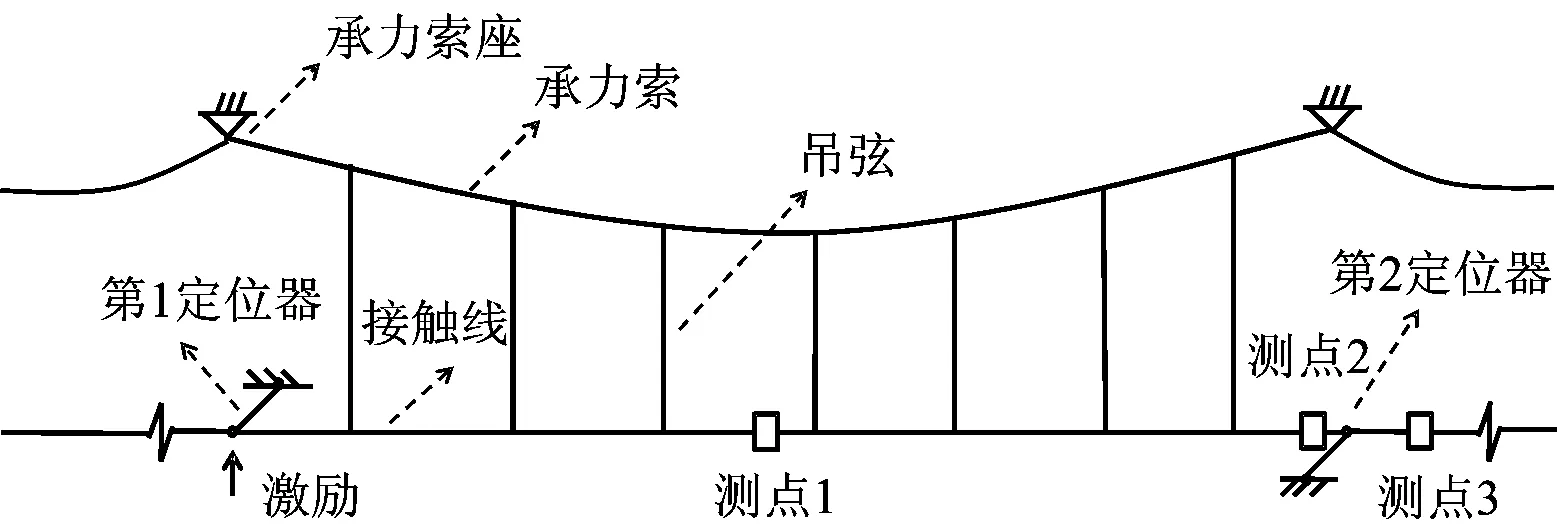
图4 接触网模型示意图

仿真计算过程中，采用欧拉梁单元建立承力索和接触线模型，用非线性弹簧单元模拟只能承受拉力的吊弦(只有抗拉刚度，抗压刚度为0)。定位器则用单质量弹簧系统等效，一端固定约束，另一端通过集中质量块连接至接触线。接触网中各线缆连接处线夹通过在相应位置处添加集中质量块模拟，接触网的详细建模方法可参见文献[15]。经有限元离散后得到的接触网常微分方程，采用Newmark-beta差分格式进行迭代求解。

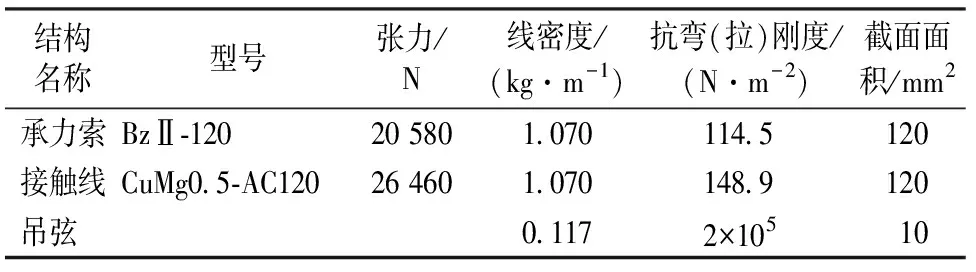
表1 接触网模型的结构参数

注：承力索和接触线的为抗弯刚度，吊弦的为抗拉刚度。

2.2 结果分析

阶跃位移激励施加在第1和第2跨间定位器处时，接触网跨中位置处的振动响应曲线如图5所示。从图5中振动位移响应来看，在阶跃位移激励突变之前，接触网跨中位置有初始抬升，约为0.052 m。阶跃位移激励突变之后，在接触网上激起弹性波，但由于弹性波传播的时间效应，该处置处接触网质点在0.18 s之前保持静止抬升状态，大约在0.2 s时刻，弹性波到达该位置，接触网跨中质点开始振动，且体现周期振动特性。

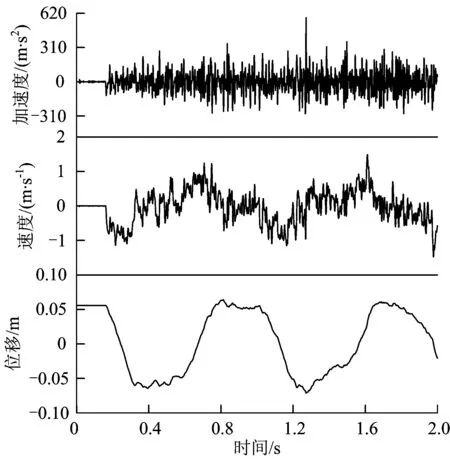
图5 接触网响应仿真结果

从前述弹性波识别理论分析相关内容来看，接触网振动位移、速度、加速度响应相应等值线图都包含有弹性波传播速度信息。但从图5中可看出，相比接触网振动速度和加速度响应，位移响应曲线更为平滑，干扰信号较少，其位移等值线图更便于识别接触网的弹性波波速。因此，绘制接触网上3跨范围内接触线各节点的位移等值线图如图6所示。

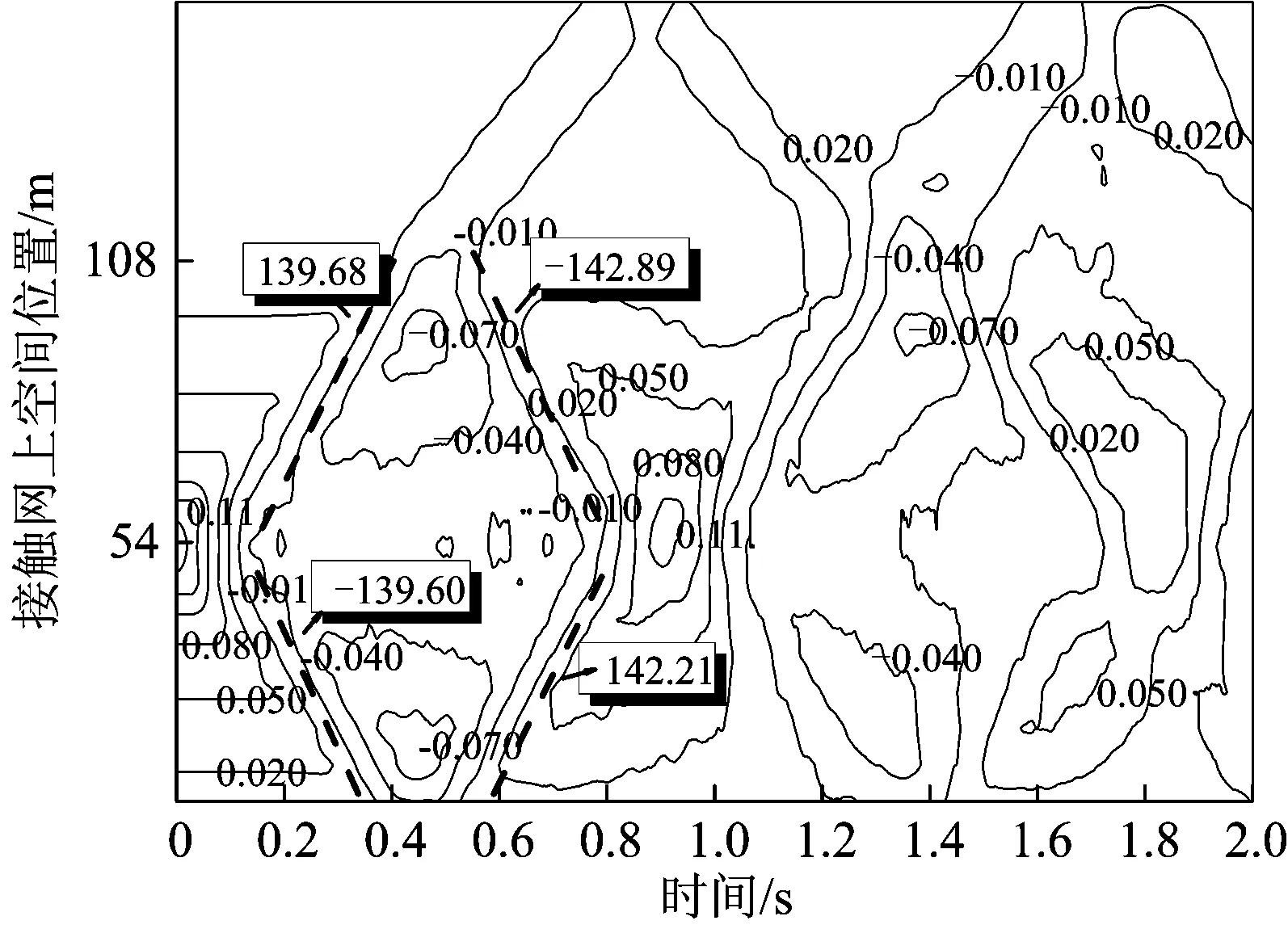
图6 3跨接触网位移等值线图(单位：m·s-1)

从图6可以看出：初始时刻的阶跃位移载荷在54 m处激起左行、右行弹性波。其中，右行波在大约0.4 s时刻抵达接触网右侧端点，并以反射波的形式继续回传。而左行波在0.4 s时刻到达第2定位器(108 m处)，并在此处同时产生反射和透射。随着弹性波在接触网上传播时间的增加，由于左右行波及其反射透射波之间的相互影响，等值线图案逐渐趋于复杂。值得注意的是，在弹性波传播的起始阶段，由于弹性波相互干涉现象尚未充分发展，阶跃位移载荷形成的左右行波，以及它们分别在第2定位器、接触网右侧端点处的反射波，共同组成1 个完整且清晰的菱形图案。

根据第1节所述弹性振动波速识别理论依据，图6中组成菱形图案的4根等值线包含有弹性波波速信息。类似1.2小节中欧拉梁波速的识别方法，利用matlab软件识别图6中虚线对应等值线的斜率，并以4根等值线斜率绝对值的平均值预测接触网的仿真波速ccate_simu=(139.68+139.60+142.89+142.21)/4=141.09 (m·s-1)。

3 接触网波速试验验证

为进一步分析以上提出接触网波速识别方法的准确性，利用3套工业相机及配套设备，基于摄影测量原理，对试验现场实际3跨接触网波速进行测试，各相机通过网线连接至控制主机，同时利用同步触发器进行数据同步。波速试验采集系统如图7所示。

接触网波速测定试验按照相机检测点位置不同分为3组工况，每组工况中又设定3种不同的激励，激励施加在图4所示第1定位器处，具体包括固定数值的初始抬升位移激励和由刚度不同的2种力锤锤头施加的定点力锤激励。9种试验工况按a-b编号，其中a为相机测点布置方案，b为激励形式。

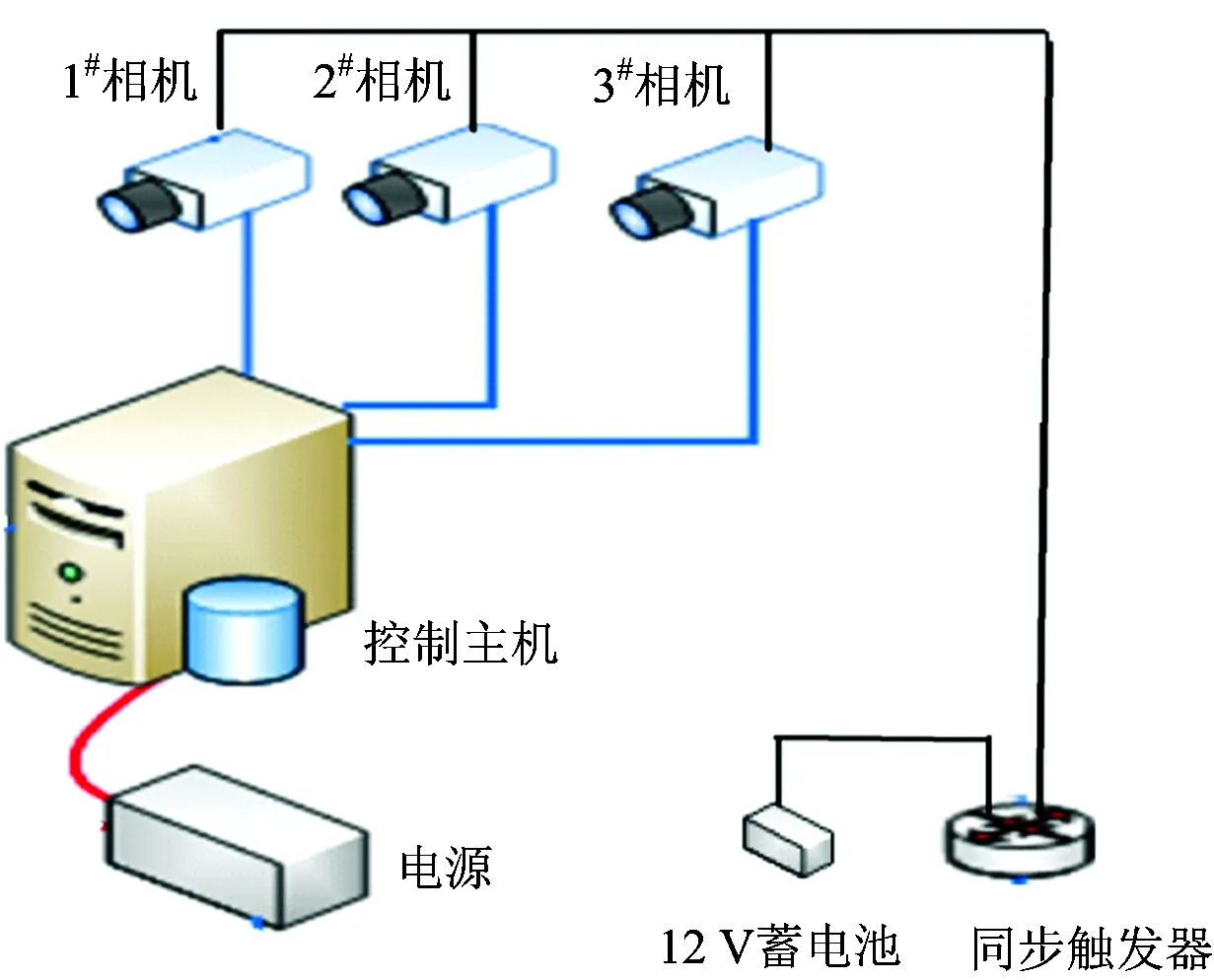
图7 接触网波速试验采集系统

图8为工况1-1中不同测点处接触线的位移时程曲线。该工况中，相机测点布置方案如图4所示，幅值为200 mm的阶跃位移激励施加在第1定位器处。从图8可以看出：由于弹性波在接触网上传播的时间效应，不同位置处测点的起振时间存在明显的时间间隔。因此，可以根据测点间的空间间隔和起振时间差确定接触网的弹性波波速。

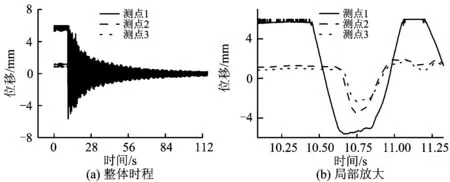
图8 不同测点处接触线位移的时程曲线

表2列出了工况1-1对应的波速测定结果。从表2中可知，3个测点两两组合后可得到3个试验波速，这里取其平均值139.24 m·s-1作为工况1-1的测试结果。

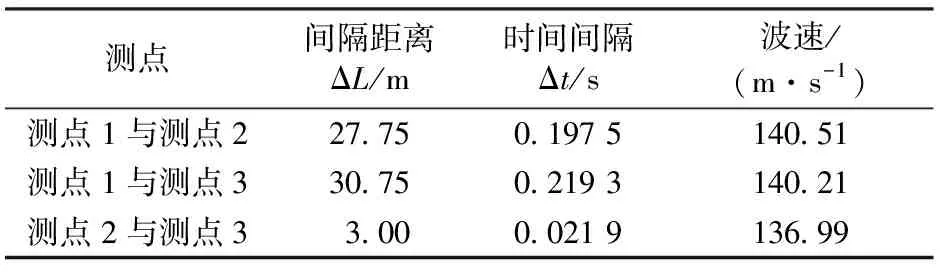
表2 工况1-1下接触线的波速

类似地，用测点间距和测点起振时间差估计所有工况下接触网弹性波的实测波速，结果见表3。从表3 中可看出：不同测试工况接触网波速测定结果重复性较高，标准差仅为1.27 m·s-1。取所有测试工况中的9个测定结果的平均值138.87 m·s-1作为接触网试验波速ccate_test的最终结果。

由第2节中接触网波速仿真识别结果可知，接触网仿真波速ccate_simu为141.09 m·s-1，与试验波速ccate_test相对误差Δsimu/test=(141.09-138.87)/138.87×100%=1.60%。

表3 接触网波动传播速度试验测试结果

由此可知，本文提出的基于位移等值线图识别接触网波速的方法准确有效，识别精度约为1.60%。同时，对于试验用的接触网室内模型，其弹性波传播速度约为139.98 m·s-1，误差在2%以内。

4 讨论及分析

波速是接触网结构设计过程中重要设计参数之一。通常情况下，工程设计人员不考虑吊弦和定位装置的影响，直接把接触网中的接触线视为单根弦或欧拉梁，依此计算出其波速来近似真实接触网的波速。

利用表1中接触线的参数，并根据试验信号中的主频频率计算单根弦或欧拉梁模型的波速，并与以上接触网试验和仿真的结果对比，见表4。

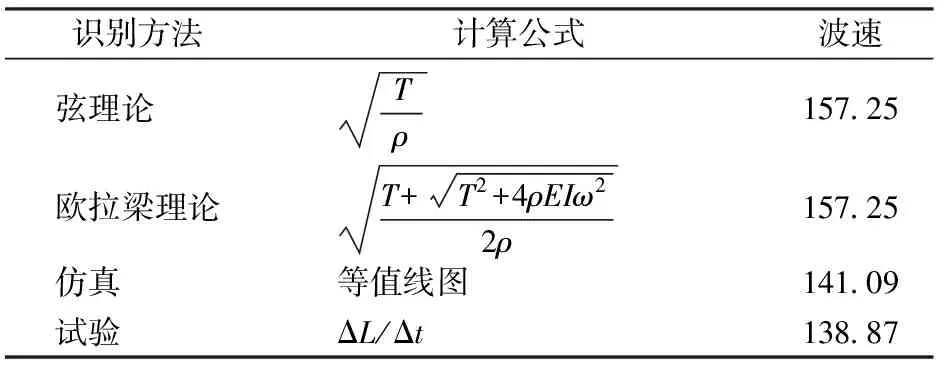
表4 不同识别方法和公式下波速的识别结果对比 m·s-1

注： 试验信号主频频率为1.189 Hz

从表4可以看出：基于弦振动理论和欧拉梁振动理论预测的接触网波动传播速度几乎一致，差别小于10-4m·s-1。一般来说，一维弹性体的抗弯刚度及其预加张力共同构成弹性恢复力。但接触网振动过程中，频率较低，接触网线缆弹性恢复力几乎全部来自其预加张力，而抗弯刚度的贡献可忽略不计。例如：由抗弯刚度而引起的等效张力Teq与预加张力T之比RTeq/T为

(4)

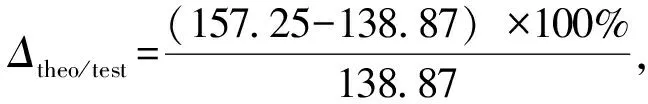
究其原因，在于理论计算接触网波速时，其计算对象实际上为接触网中被视为单根弦或欧拉梁的接触线。相比该单根接触线，实际接触网中弹性波在传播过程中会在吊弦和定位器处发生反射，从而等量的弹性波波动能量在实际接触网上传播同样的距离耗费的时间更长，因此试验和仿真结果要低于理论计算值。此外，通常情况下，弹性波的波速正比于弹性介质弹性力，而反比于介质惯性力。实际接触网结构中的接触线与单根接触线相比，连接至其上的承力索、吊弦等附属结构提升了接触线保持其原有振动状态的能力，即增加了其惯性力，但不改变接触线中预加的张力，即不影响其弹性力，从而单根接触线的波速也相应高于实际接触网的波速。可预见的是，不考虑吊弦和定位器的影响时，针对单根接触线采用弦或欧拉梁理论计算出的波速，将高估实际接触网的波速，降低其波速利用率的安全裕度。

5 结 论

(1)基于时空坐标下位移等值线图识别弹性波波速的方法能够用于识别接触网波动传播速度，精度在2%以内。

(2)由试验测试结果和仿真识别结果可知，3跨接触网的波速约为139.98 m·s-1。

(3)基于欧拉梁或弦振动理论，用单根接触线的波速计算值近似预测接触网的波速，预测结果相比实测值偏大13.23%。原因在于实际接触网中吊弦和定位器处的弹性波反射与透射，降低了波动能量在接触线上的传输效率。